动态组网高精度双向时间同步技术研究*

齐小刚，袁列萍，刘立芳

(1.西安电子科技大学 数学与统计学院，西安 710071；2.西安电子科技大学 计算机学院，西安 710071)

0 引言

随着计算机网络、无线通信、电子等技术的快速发展，动态组网因高健壮性、强抗毁性、低截获性、自组织性等优势在抢险救灾、交通监测、航天航空、导航定位等各个领域得到广泛应用[1]。尤其是在军事中，移动或固定终端随机入网、资源监测并动态调整、基于优先级方式优化竞争等需求更是突显了动态组网的重要价值。动态组网是一种独立于固定基础设施搭建的临时自治网络，各个节点随机运动且均配有收发装置，能够接收并发送一定量的信息[2]。网络的动态性和自组织性使得各个终端获得通信便利的同时，终端设备时钟不匹配问题使得终端无法无差错的协调工作，这一瓶颈难题给动态组网进一步扩展应用带来了新的挑战和机遇。节点的随机加入及退出、位置不固定、速度及移动方向不可预测等特点使动态组网节点同步变得十分困难[3]。现有高精度时间同步方法大多集中于静态站[4-5]，动态站[6-7]研究较少。然而，现实生活中的很多应用，同步的终端设备已经不再局限于静态，往往是移动的，这使得同步方法不仅需要适应动态、自组织的网络，而且算法应具有灵活、精度高、抗干扰能力良好、通信开销低、可靠性高等特点。因此研究适应动态网络的高精度时间同步方法迫在眉睫，高效、高精度且计算复杂度低的动态站时间同步方法不仅具有延长动态组网寿命，实现系统运行的可持续性等优点，而且对我国航天、军事等发展将起到至关重要的作用。

1 经典的时间同步技术

根据时间同步过程中数据的传输方向和交互方式差异并结合文献[6]的分类优势，经典的时间传递技术大体上可归纳为两类：单向时间同步和双向时间同步，如图1所示。

图1 时间传递技术分类

1.1 单向时间同步

单向时间同步技术[8-13]指根据信号在传输媒介的单程时延，在接收端进行时延补偿，进而实现时间同步的过程。其中，GNSS时间传递法是应用最广泛的时间传递方法之一，主要分为单向时间传递[7]、共视时间传递[8]、全视时间传递[9]、精密单点定位(PPP)[10]四种方法。①GNSS单向时间传递具有低成本、信号覆盖率高、可为多用户服务的优点，但时间传递受大气和星载钟的影响较大，同步精度不高。②GNSS共视时间传递法原理如图2所示，该方法通过两单向传递结果作差消除了卫星钟与系统之间的钟差，且星载钟误差，大气时延误差等部分抵消，有效提高了时间同步的精度；但待同步两站必须观测同一颗卫星，一定程度上对两地的共视距离有限制，不能进行全球任意位置间的时间比对。③GNSS全视时间传递法原理如图3所示，待同步节点独立跟踪多颗卫星，不受距离限制，可实现全球任意位置时间同步，然而该方法容易受星载钟和星历误差的影响。④精密单点定位(PPP)原理与全视类似，只是数据处理方式不同，该方法精度很高但算法复杂，难以适用实时性要求较高的系统。

图2 GNSS共视基本原理

图3 GNSS全视/PPP基本原理

1.2 卫星双向时间同步

双向时间同步技术[14-15]原理如图4所示，待同步的两站通过卫星发送时间信息给对方并接收对方传输的时间信息，结合对流层、设备时延等影响因素进行修正，计算出两站的钟差。该方法因传输路径近似对称，路径时延可以忽略，精度较高。发射和接收路径相同，方向相反，消除了卫星、测站位置误差的影响，最大限度地降低了电离层、对流层时延误差的影响，而且通信卫星较宽的带宽有利于信号设计，受温度、湿度等影响较大，但可通过有效手段进行修正使影响控制在可接收范围内。与单向时间同步方法相比，卫星双向时间同步具有如下显著优势：

①传输路径时延可大部分抵消，因而同步精度较高。待同步节点为静态站时，传输路径对称，可忽略传输路径造成的误差；待同步节点运动时，传输路径近似对称，大部分传输时延可被抵消。

②待同步节点间距较小时，无需中继转发，即可通过节点间互发测距信息，实现时间同步；比对时间短，实时性高。

③可靠性高，适用动态拓扑。

图4 卫星双向时间传递基本原理

2 动态组网双向时间同步原理

在短距离直发直收情况下，假设任意动态节点A与节点B实现时间同步，在系统t时刻，节点A和节点B互发互收测距信号，并计算相应伪距值；节点A将自己的伪距信息、发射时刻、接收时刻等信息通过数据链发送给节点B；节点B根据自己的伪距信息、发送时刻等信息结合接收到的节点A的信息，进行钟差计算，进而实现两节点的时间同步，图5给出了动态节点双向时间同步框图。

在系统t时刻，两动态节点同时发送测距信号，根据动态节点双向时间同步框架及其监测反馈原理得到伪距的计算表达式如下：

(1)

式(1)中，ρAB和ρBA分别表示A到B和B到A的伪距；lAB和lBA分别表示A到B和B到A的真实几何距离；ΔtAT和ΔtBT分别表示A和B的发送时延；ΔtAR和ΔtBR分别表示A和B的接收时延；ΔtAB和ΔtBA分别表示A和B的自由空间传输时延；δB-δA表示A和B的时差；ε表示其他噪声；c表示光速。

根据公式(1)可得到钟差的计算公式为

(2)

图5 动态节点双向时间同步框架

在动态组网中，由于节点的动态性，节点之间的真实距离无法实时得到，而双向时间同步方法可通过运算，抵消节点真实几何距离项，得到钟差，消除了真实距离计算带来的误差，使得时间同步精度更高。在节点位置未知情况下，钟差计算方法如下。

式(3)和式(4)为系统时刻t时两动态节点A和B发送和接收时刻的关系方程。

节点A和B发送时刻的关系式：

(3)

节点A和B接收时刻的关系式：

(4)

式(3)和(4)中，tAS为A的发送时刻，tBS为B的发送时刻，δtAS和δtBS为A和B发送的瞬时钟差。tAR和tBR分别为A和B节点的接收时刻，τBA为信号在B节点产生到A节点接收整个过程的传输时延，τAB为信号在A节点产生到B节点接收整个过程的传输时延。

将式(3)代入式(4)中，两式作差得

(δtAS-δtBS)+(tAR-tBR)=(δtAS-δtBS)+(δtAR-δtBR)=

(δtAS+δtAR)-(δtBS+δtBR)=τAB-τBA。

(5)

因τBA为信号在B节点产生到A节点接收整个过程的传输时延，τAB为信号在A节点产生到B节点接收整个过程的传输时延。从而τBA-τBA包含了真实几何距离时延、设备的发送接收时延，自由空间的大气传输时延及其他噪声时延。即

(6)

将式(5)和式(6)代入式(2)中可得到

(δtAS+δtAR)-(δtBS+δtBR)=τAB-τBA≈(ρAB-ρBA)/c。

(7)

因此，在节点位置未知情况下，通过位置抵消可得到两同步节点钟差。

3 动态组网双向时间同步的重要影响因素

为建立动态组网时间同步方案，探寻和分析动态组网双向时间频率传递的影响因素是构建时间同步模型的先决条件，准确高效地评估各个影响因素对实现时间同步的影响状态是修正和调整钟差的必经之路。本文综合考虑双向时间同步的原理及节点的动态性能，在短距离直发直收情况下，将影响时间双向同步的因素归纳为3个方面，如图6所示，分别为节点运动造成的Sagnac效应路径不对称时延、自由大气传输中的电离层和对流层时延及用于进行时间同步的发送和接收设备时延。

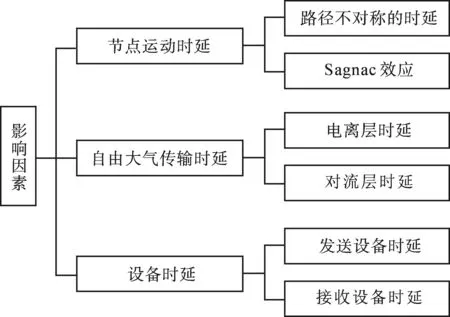
图6 动态组网双向时间同步影响因素

3.1 动态节点Sagnac效应几何路径时延

在动态组网中，节点处于不断运动中，产生的Sagnac效应[16]造成双向传递路径不对称，进而产生路径时延误差，原理如图7所示，修正Sagnac效应对时间同步的影响是提高时间同步精度的核心环节。

假设参与时间同步的动态节点A和B，在系统t时刻发送同步信号时，分别位于S1和S3位置处，由于节点运动，A和B节点接收到对方信号时分别位于S2和S4位置处。Sagnac路径时延计算公式推导如下：

①A和B为位置已知的锚节点,其中A的Sagnac效应时延为

ΔtAS=(|S3-S2|-|S3-S1|)/c，

(8)

B的Sagnac效应时延为

ΔtBS=(|S4-S1|-|S3-S1|)/c，

(9)

式(8)和式(9)中，S1,S2,S3和S4为位置矢量。可以得到A和B双向链路因Sagnac造成的链路时延误差为：

ΔtSa=ΔtAS-ΔtBS=(|S3-S2|-|S4-S1|)/c。

(10)

图7 动态节点Sagnac效应原理图

②A和B为位置未知的随机动态节点。

若节点位置未知，则无法用公式(10)计算链路时延误差，本文通过已有的时钟时刻信息及其节点运动速度信息，推算与距离的关系，进而得到位置未知条件下动态节点的链路时延。

动态节点A和B的运动矢量方程为：

(11)

式(11)中，VAR为节点A接收时刻的瞬时速度，VBR为节点B接收时刻的瞬时速度。

将式(11)代入式(9)中，即可得到位置未知时动态节点的链路时延：

ΔtSag=(|S3-S2|-|S4-S1|)/c=(|S1-S4+DA+DB|-|S4-S1|)/c≤(|DA|+|DB|)/c≈ (|VAR×(tAR-(tAT+ΔtAT))|)/c+(|VBR×(tBR-(tBT+ΔtBT))|)/c。

(12)

由式(12)可知，节点位置未知时，精确的动态节点速度估计是计算链路时延的关键。

3.2 大气传输时延

自由传输空间的时延误差主要来源于大气中的电离层[17]和对流层[18]，当信号经过对流层和电离层时，因为折射、散射、反射、吸收等，路径产生弯曲或偏移原来路径，造成测距误差，采用或建立合理模型精确估计大气传输时延是进行测距修正的重要步骤。

①电离层时延。在双向时间频率传递中，动态节点A上下行链路的电离层时延差可用如下公式[19]表示：

(13)

式(13)中，Ttec,A是节点A的电离层总电子含量，fU代表上行信号频率，fD代表下行信号频率。

电离层对链路站A到B产生的延迟为

(14)

电离层对反向链路B到A产生的延迟为

(15)

式(14)和(15)中，Ttec,B为节点为B的电离层总电子含量。

②对流层时延。对流层延迟主要由大气中的干燥气体和水汽引起，可统一化计算公式[20]为

ttrop=tdry+twet,

(16)

式(16)中，ttrop，tdry和twet分别表示对流层延迟、对流层干延迟和对流层湿延迟。

根据实际情况及同步场景进行式(16)细化计算。常用的对流层模型有Hopfield模型[19]、Saastamoinen模型[21]、EGNOS[20]模型、GMF模型[22]和Marini模型[23]等。

3.3 设备时延

设备时延主要指发送和接收设备时延[24-25]。目前，设备校准方法主要有绝对校准和相对校准[24]，本文以卫星模拟器法、单移动和双移动站法3种典型方法进行了详细比较分析。

卫星模拟器校准法先求出待同步站发射和接收设备时延和，再求出调制解调器(Modem)的发送和接收时延和，利用示波器得到Modem的发送时延，进而求出Modem的接收时延；通过一系列操作，得到卫星模拟器到Modem射频输入和输出口的时延，最终求得设备的发送接收时延差。

单移动站法主要有SITE和LINK法两种，图8和图9展示了两种方案的校准过程。①SITE校准：将移动站分别放到待同步站1和站2处做零基线共钟比对，得到移动站与站1和站2的时延差，再将两个时延差相减即可得到设备的时延差。②LINK校准：第一步将移动站放到站1处进行零基线共钟比对，得到移动站与站1的时延差；第二步将移动站放到站2处，与站1做双向时间比对，结合第一步得到的时延差，得到站1与站2的传输时延；第三步将站1与站2做双向时间比对，得到站1与站2的总时延差，再减去第二步得到的传输时延，进而得到设备的时延差。

图8 单移动站SITE校准方法原理

图9 单移动站LINK校准方法原理

双移动站法[26-27]原理如图10所示，第一步将两个移动站都放到站1得到设备零值；第二步将两个移动设备分别放到站1和站2，进行双向时间比对，得到总的时延；第三步将两个移动站放到站2处，得到设备零值；将第一步和第三步得到的设备零值平均后作为移动站设备的零值，再将该值代入第二步得到，得到双向链路的时延；第四步，利用站1与站2进行双向时间比对，得到时延；第五步将第三步和第四步得到的时延相减即可得到站1与站2 的设备钟差。

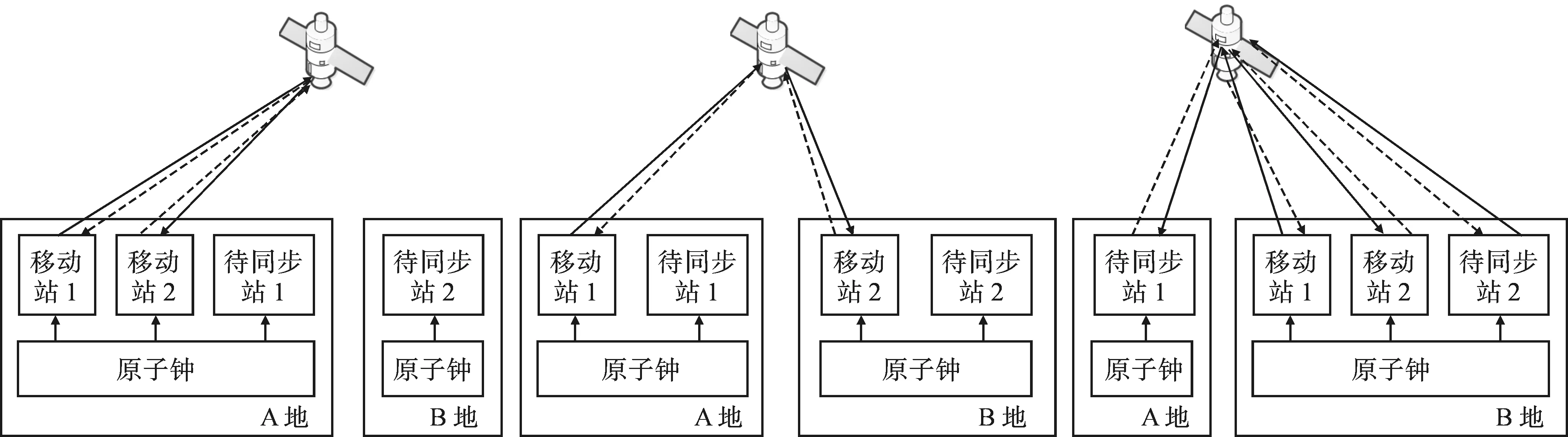
图10 双移动站校准方法原理

表1比较了3种设备校准方案的性能，结果显示各个方法都有缺陷，为提高设备校准精度，可将卫星模拟器法和移动站法结合：对于静止节点，利用移动站法进行长期校准，同时利用卫星模拟器法进行连续测量弥补校准数据的不足，两套系统同时应用在同一校准站，两组测量数据相互对比检验，可提高双向时间同步校准系统的置信度[27]。然而动态组网运动状态处在不停变化中，周围环境噪声、各种干扰使得时钟不断漂移和抖动，无法一次校准保持不变。文献[28]提出了一种基于各个监测站点监测数据实现卫星双向设备时延的校准方法，通过监测可用双向比对数据并进行事后数据处理的方式校准两地卫星双向设备的时延差，该方法实现简单、成本低、精度较高。动态组网节点的动态变化难以预测，基于信息(包括数据包传递信息、发射信号信息等)的设备时延估计方法值得深入研究。

表1 常用设备时延校准方法性能比较

4 开放性问题

截止目前，动态组网时间同步技术广泛开展并取得了许多研究成果，但仍存在一些开放性问题值得进一步研究。

①动态组网内部的多址干扰抑制。动态节点进行时间同步时，多址干扰对通信质量和系统同步有很大的影响，为提高时间同步精度，进行多址干扰抑制是首要解决的问题之一。已研究的成果主要分为多用户检测[29]和多址干扰抵消[30-31]两种算法，算法的最终结果展现在提高检测性能和降低算法计算复杂度两个方面，在算法性能方面多用户检测算法优于干扰抵消算法。已有算法只是通过优化信号体制对干扰进行了一定的缓解。因此，高效的多址干扰抑制技术是改善时间同步技术精度的突破口之一，仍值得进一步研究。

②动态节点组合时间同步方案研究。动态组网内部因用途、环境、运动状态等不同，并非所有节点都需要同样水平的时间精度。若使用统一的时间同步方案，又必须适用所有节点，满足所有节点的精度要求，在一定程度上增加了硬件的成本、软件算法复杂度等，因此针对动态组网内部节点的动态特性和精度要求进行具体问题具体分析是十分有效的处理措施。文献[32]针对低动态、中动态、高动态3种运动情况给出了相应的硬件或软件时间同步方法，该方法高效地解决了动态节点的时间同步问题。在动态组网中，建立适用不同运动状态的时间同步方案是十分有效的。主要处理方法可为：给节点做一个简单的判断模块，对发送时间同步请求的节点进行运动状态的判断，进而调用不同的时间同步方案，这样实现简单，经济实用。

③高传输速率的数据链路设置。信息传递是双向时间频率传递的基石，时间同步的精度直接依赖于传输链路的性能。目前使用频繁的数据链主要有LINK 16[33]和TTNT[34]，而LINK 16通常用于预先人为规划的静态网络，不适用于动态组网；TTNT数据链以IP协议为基础，采用Ad hoc技术的网络，能够迅速瞄准移动和时间敏感目标且具有高吞吐量、高传输速率、低传输时延、网络鲁棒性强等特点[34]，因此TTNT数据链成为时间同步信息传输首选。研究和建立高速的数据链路是实现动态组网高精度时间同步需解决的关键问题之一。

④建立实时伪距预测模型。伪距计算是双向时间同步的核心环节，已有的伪距计算主要采用时间间隔期多次测量数据平均[35]得到，这种方法耗时，不具备实时性。基于前一时刻信息的伪距估计模型[36]能够在短时间内根据已有信息估计当前时刻伪距值，算法精度高。在动态组网中，将基于时间间隔计数器的仪器测量和基于信息的估计模型相结合的伪距估计模型将是一种十分实用的方法。实现的步骤大体为：可设定时间阈值，在阈值范围内，通过估计模型实时估计伪距，若超出阈值范围，则采用仪器测量方法进行伪距测量。这样既可保证伪距测量的精度，又可满足动态组网实时性的要求。

⑤高效的频差估计。文献[37]给出了时差与频差之间的关系，指出时钟的频率误差会产生时钟频率漂移，进而引起钟差的改变。在进行时间同步时，单纯只校准时钟钟差，只能维持小段时隙内时间的同步，一段时间之后，已同步的时间会因为频率漂移产生偏差。在动态组网中，节点运动导致原子钟受温度、力频等因素影响，频率出现漂移，造成时间同步误差；为实现高精度的时间同步，必须保证良好的频率稳定度和频率准确度，因此高效的实时频差模型是未来时间同步精度提高研究的重点。

⑥可靠的多普勒频移估计。多普勒频移指信源相对于接收节点是不断运动的，其径向速度将对调制信号产生多普勒效应，进而导致接收节点进行信号解调时形成较大频偏的过程[38]。当多普勒频移超出捕获带或频偏率过大时，会造成环路失锁，无法进行信号捕获和跟踪[39]。因此多普勒频移的研究对实现信号捕获跟踪及载波同步意义重大。目前，多普勒频移的解决方法主要可归纳为两大类：一是对锁相环路的宽度捕获和动态范围跟踪进行改善[40]，该方法会影响系统的其他性能，例如加长信号捕获时间等，且该方法适应的时变范围有限，算法性能受信噪比的制约；二是通过多普勒频移估计进行频偏补偿或消除[41]，基于这种思想，文献[42]提出了一种多普勒频移的快速估计和实时补偿算法，该方法计算复杂度低，实时性好且不依赖接收机的信噪比，对大频偏信号的快速跟踪和解调具有一定的参考价值；文献[43]以高动态载体在临近空间中的简单运动模型为依据，仿真分析了高动态载体相对于临近空间平台的多普勒频移变化曲线，通过变化曲线，可动态调整捕获跟踪方案，提高跟踪精度。在动态组网中，动态两节点实现时间同步时，因波源与接收节点有相对运动，使得接收节点接收到的频率与波动频率产生差异，进而导致接收节点信号解调时形成较大的载波频偏，为解决这一问题，可借鉴第二类多普勒频移估计并补偿及动态调整捕获方案的思想，抑制多普勒频移对信号捕获跟踪及载波同步的影响。

5 结语

随着计算机与通信技术的迅猛发展，动态组网平台下的各种应用已经渗透到人们生活的各个方面。如何保证各个控制平台、监测平台、指挥平台等处在统一时间尺度下工作，是动态组网技术广泛应用的核心需解决的问题，因此研究基于动态组网的高精度时间同步技术意义重大。本文对动态组网时间同步关键技术进行分析总结。重点研究了基于动态组网双向时间同步技术，推导了在节点位置未知状态下的钟差解算公式和Sagnac效应时延公式，并讨论了动态组网框架下的开放性问题，希望能为研究者设计更加精确的动态组网时间同步方案甚至最终推动动态组网的部署发展及基于时间同步的系统构造、仪器检测、导航定位等领域的研究给出有意义的启示。