一种基于技术状态变更的可靠性综合评估方法*
2019-06-14鞠成玉杨胜学王守敏
鞠成玉,杨胜学,王守敏
(中国飞行试验研究院,西安 710089)
0 引言
试验与评定是装备研制系统工程中的一个有机组成部分,它的作用是确定性能水平,帮助研制者纠正缺陷,同时也是决策工程的一个重要环节,为权衡分析,降低风险和细化要求提供支持性信息。
现阶段航空武器装备在设计定型试验阶段可靠性评价仍存在失效分布模型选择单一,精确度不足的情况,评价模型主要利用指数模型,但是指数分布存在适应性差,美国NASA对复杂系统进行统计后发现,复杂系统故障失效分布曲线服从指数分布的仅占总体的18%,剩余82%服从其他类型分布(见下页图1),故全部选用指数分布对可靠性评估结果具有较大影响。

图1 故障失效分布曲线
目前,我国航空武器装备设计定型期间,受经费、周期及研制单位研发进度的限制,同型号不同飞机状态不一,即使同一飞机,试飞早期和中后期也存在一定差异,飞机技术状态变更较多,导致在此期间产生的评估结果与装备部队后实际可靠性结果存在较大的差异,故对航空武器装备进行可靠性评估时,需考虑缺装产品或非鉴定状态产品可能造成的故障对整体可靠性指标的影响。
另一方面,受经费等限制,投入设计定型期间的航空武器装备试验品较少,造成评估故障样本量偏低,对于可靠性评估精度产生较大影响,因此,如何充分利用航空武器装备实验室等内场数据,将其与设计定型试验数据进行数据融合,提高评估结果精度,是目前研究的一个热点问题。表1显示某型飞机设计定型期间技术状态变化情况。

表1 某型飞机状态变化情况
1 解决思路
本文针对上述问题,提出如下解决思路:
1)通过对技术状态的更改进行有针对性选取被更改的单元作为最小组成单元;
2)当最小组成单元在设计定型期间的失效数据样本量充足时,则直接对其进行基于多种失效分布的建模计算;
3)对于设计定型期间数据量不足的最小组成单元,采用贝叶斯数据融合的方法进行建模分析;
4)最后汇总各最小组成单元的失效分布模型,根据系统的结构关系,采用蒙特卡罗方法,给出系统可靠性综合评估结果。具体思路见图2。
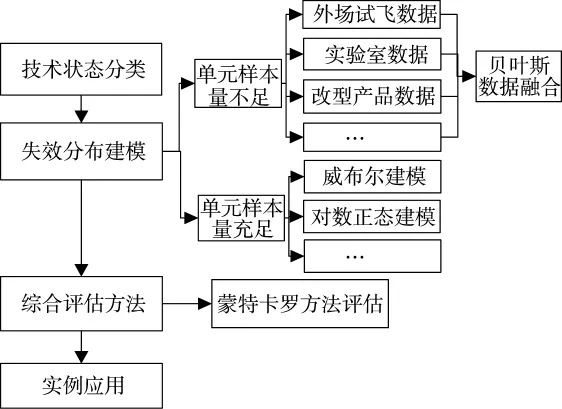
图2 解决思路图
2 算法实现
针对上述解决思路,本节从系统拆分最小组成单元原则、数据建模、数据融合、系统综合评估方法等4部分分别进行研究。
2.1 系统拆分最小组成单元原则
如何合理选择系统的最小组成单元,并且能够体现出产品的技术状态变更,是计算成败的关键内容。本文选取的最小组成单元的原则为入选的更改单元以对整机可靠性影响较大,如果技术状态变更过程中仅仅针对软件及基本不发生故障的微小部件的更改,则不纳入最小组成单元系统的故障数据统计中,最后将拆分的最小组成单元组合成技术状态完整的大系统或整机。
2.2 数据建模
当最小组成单元失效数据样本量充足时,则直接对各系统设备所服从的失效分布进行精确计算。从图1中可以看出,服从指数分布的浴盆曲线与故障率恒定的占总体的18%,其余可利用威布尔分布和对数正态分布等失效分布函数进行建模,故本文选取指数分布、威布尔分布、正态分布及对数正态分布4种分布作为航空武器装备失效分布的研究对象。本文以威布尔分布为例进行建模过程分析,其他分布模型同此过程[1],在此不再赘述。
威布尔分布的累积分布函数F(t)为:
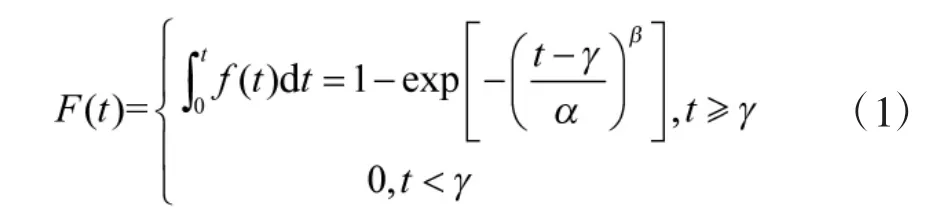
在工程应用中常假定γ=0。它的含义是:从开始试验起,在任何时间都有可能发生故障。线性回归分析是求解分布参数的常用方法,对式(1)进行变换,并取自然对数并令

从而将威布尔分布变换为y=A+Bx线性函数。然后用最小二乘法得出参数A、B的估计量,最后通过线性相关性检验和柯尔莫哥洛夫-斯摩洛夫(K-S,Kolmogorov Smirnov)检验进行参数检验即可。
2.3 数据融合
2.3.1 贝叶斯建模
当设计定型期间,最小组成单元失效数据样本量不足时,本文利用Bayes理论的融合方法[2-6],通过引入折合因子来表征不同母体的故障信息之间的差异,并对故障信息进行折合,从而实现目标产品的精确寿命评估。下面以威布尔分布为例进行数据融合过程分析,其他3种分布模型同此过程,在此不再赘述。
对于两组数据X1,X2而言,假设X2为先验故障数据,X1为目标产品的数据,且 X1~W(β1,α1),X2~W(β2,α2),为了建立先验数据信息与样本数据信息之间的关系,引入修正因子k21,k22,使得
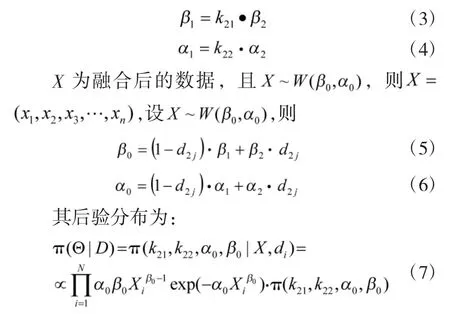
2.3.2MCMC求解方法
对于上节中建立的两参数威布尔分布融合模型,采用MCMC方法对未知参数进行随机抽样模拟[7-10]。对于先验分布的选取,参考相关文献[11-12],令,l取正态分布,β取Gamma分布;考虑到k21,k22必须为正数,并结合具体情况,可考虑具有对数凹性的分布形式,故均取形状参数大于1的Gamma分布。假设用MCMC方法求解上式未知参数后验分布的参数迭代示意图,如图3所示。最后需判断马尔可夫链的收敛性以及MC误的大小[13-16],如果马尔可夫链收敛且MC误比较小,则分布计算结果可以作为最终的计算结果。
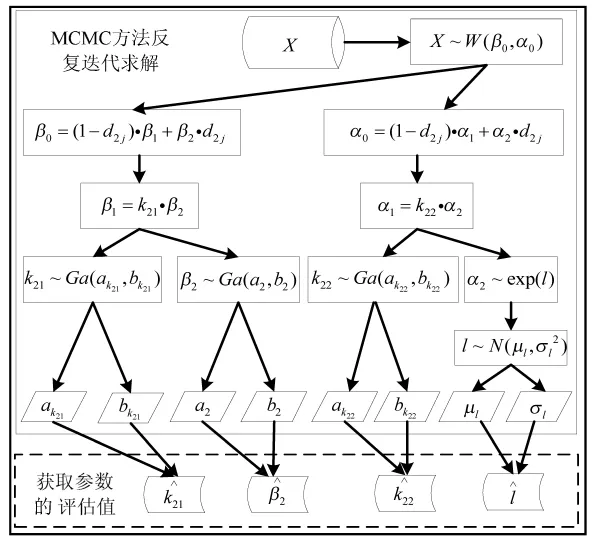
图3 两参数威布尔分布融合模型参数迭代示意图
2.4 系统综合评估方法
由于系统的组成结构复杂,实际设备寿命数据的类型多为截尾数据等,难以给出系统可靠性指标的解析表达式,本文利用蒙特卡罗方法的计算优点,同时结合系统的结构关系,采用计算机仿真的方法给出系统可靠性综合评估结果[1]。
2.4.1 综合评估模型

2.4.2 系统可靠性综合评估算法
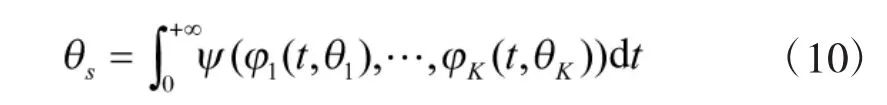
然后利用式(10),通过蒙特卡罗方法,可以得到系统可靠度与平均寿命的仿真抽样结果,然后以与置信度对应的分位数为置信限,进而得到区间估计。计算系统可靠度与平均寿命置信分布的步骤具体如下:
1)利用2.4.1中的方法把每个设备可靠度Ri(t)的置信分布表示成,其中,这里Gi为已知分布;
2)置循环变量k=1,生成不同设备可靠度置信分布参数θi的随机数

3 实例验证
某型飞机有4架投入使用飞行试验,其中技术状态变化参照表1所示。
3.1 最小单元选取
根据2.1节系统拆分单元原则和方法,对表1中飞机技术状态变化,将其划分为雷达、电子战系统、发动机、红外搜索系统、其他部分为组成单元进行计算。
3.2 数据建模
除电子战系统、红外搜索系统外,雷达系统、发动机、其他组成系统在飞行试验中失效样本量充足,以发动机为例,利用MATLAB绘制发动机失效概率图形,如果原始数据是威布尔分布数据,那么图形是直线排列,否则图形会发生弯曲,从图4~图7可以看出,发动机失效数据与威布尔分布非常接近,故可得出该组数据可能服从的分布类型是威布尔分布。
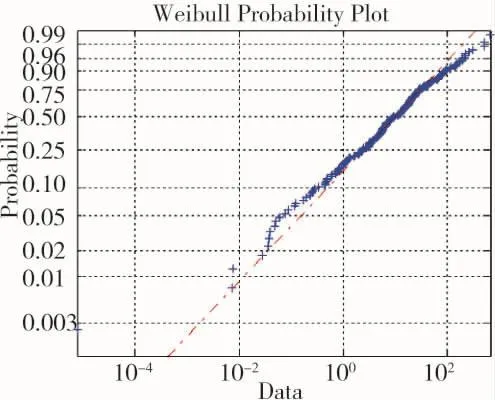
图4 威布尔概率图形
使用2.2节数据建模方法进行建模分析,最终得到3个系统的失效累积分布函数为:
雷达系统:
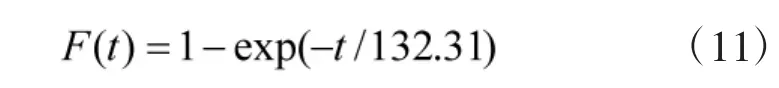
发动机:
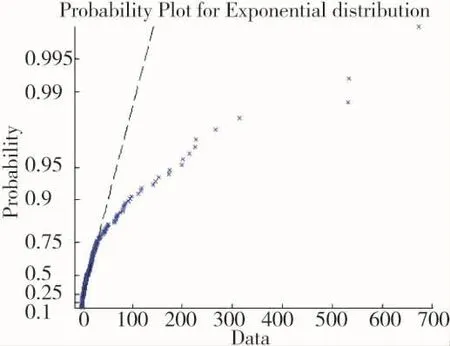
图5 指数概率图形
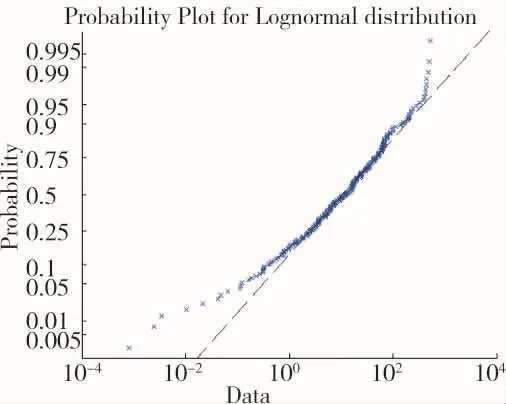
图6 对数正态概率图形

图7 正态概率图形
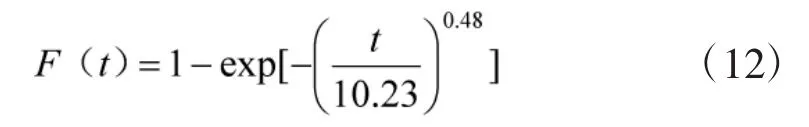
其他组成系统:
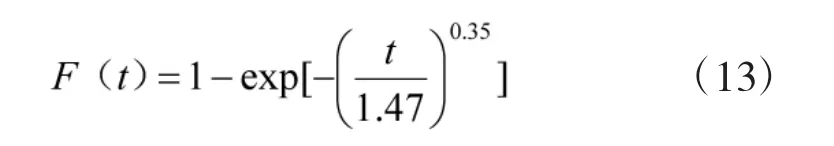
3.3 数据融合
电子战系统由于外场样本量不足,只有5个失效数据,但是电子战系统内场失效样本量较多,有35个数据。利用第2.2节内容计算,对内场失效样本量进行拟合并确定最优分布,最终得到最优拟合分布为威布尔分布,成立概率为94%,其内场累计失效概率函数为
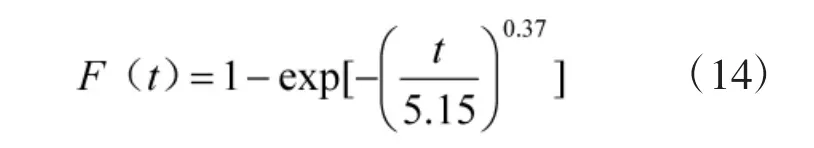
引入折合因子k21,k22,利用2.3节的融合模型进行数据融合。对于先验分布的选择,k22取伽马分布,k21可取伽马分布或者指数分布,这里取指数分布;α2取对数正态分布,β2伽马分布。图8为Winbugs软件计算界面:
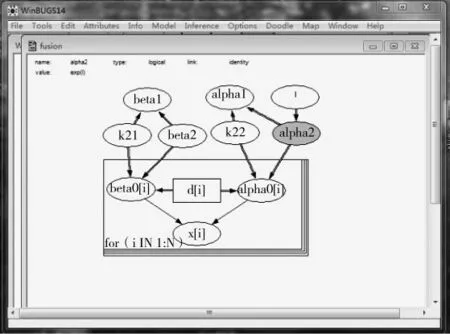
图8 Winbugs界面
则未知参数计算结果见表2。
另外,未知参数 k21,k22,α1,α2,β1,β2的 MC 误均小于样本SD(标准差)的5%,因此,可以用MCMC方法得到的未知参数后验分布进行贝叶斯推断。则外场的可靠度函数为
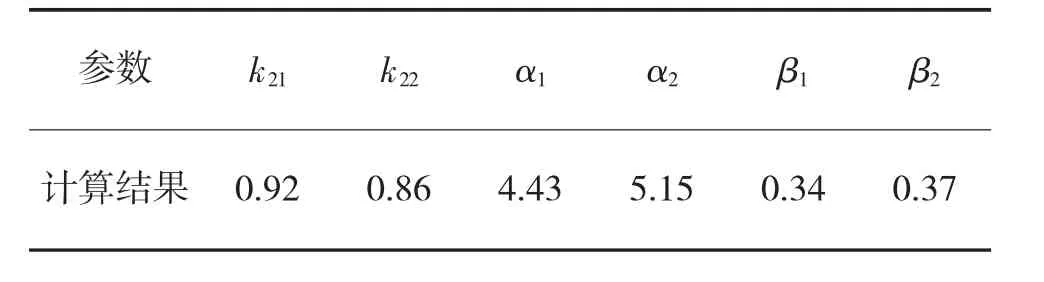
表2 故障数据融合参数计算结果
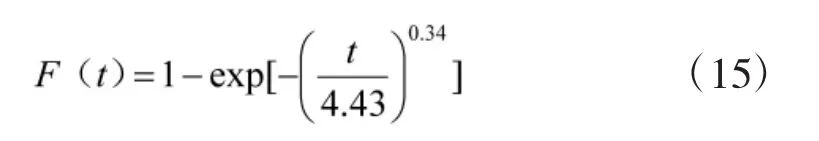
红外搜索系统与电子战系统相类似,最终计算出其外场失效模型为
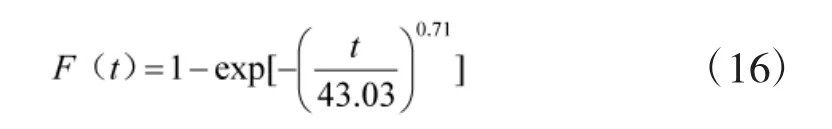
3.4 综合评估
系统连接的结构关系均为串联连接,故建立如图9所示的连接图。

图9 系统连接图
4 结论
本文针对航空武器装备在设计定型试验阶段失效样本量少,技术状态变化频繁的问题,提出利用贝叶斯方法进行相似产品数据的融合及建模,然后利用蒙特卡罗方法进行综合评估,最终得出产品的置信下限,对于航空武器装备设计定型期间技术状态变化频繁、失效分布单一等情况具有较好的指导意义和工程应用价值,对于后续开展可靠性评估具有重要意义。
