空间飞行器的姿态和扰动抑制控制器设计*

沈 培 ，贾付金 ，罗家维 ，3，李伯勋 ，苏 啸

（1.萍乡学院机械电子工程学院，江西 萍乡 337000；2.南昌航空大学信息工程学院，南昌 330063；3.江西工业工程职业技术学院，江西 萍乡 337055）

0 引言

最近几十年以来，因为姿态控制系统是空间飞行器总体设计的重要组成部分之一，所以姿态系统已经并将继续成为广大学者的热门研究对象。鉴于飞行器系统中转动惯量因为燃料消耗等因素存在的不确定性和受到外部未知的干扰。所以，寻求一种不依赖矩阵惯量和干扰信号，并且还要使得系统状态全局稳定的控制器成为国内外广大学者研究的热点之一。

目前，在不确定参数和外部干扰的影响下，飞机的姿态控制问题还没有被考虑进去，已经进行了广泛的研究［1-7］。LUO等人［8］提出了一种逆最优自适应控制方法来解决参数的不确定性和外部干扰对飞机的影响。其解决了已知的飞机姿态跟踪与有限能量干扰问题。为了克服干扰信号能量有界的假设，CHEN等人［9］四元数用于描述飞行器的姿态，通过自适应控制理论和输出调节理论的内部模型方法，将干扰信号恒定和有限数量正弦信号的形式结合假设条件，进一步研究航天器姿态跟踪和干扰抑制问题；但是根据文献［10］可知:单位四元数描述的飞行器姿态会使得方程有两个平衡点，而且其中有一个是不稳定的。为了克服利用四元数描述姿态带来这样的缺陷，刘献平［11］采用了 Rodrigues参数［12］来描述飞行器姿态，并利用Backstepping控制方法、自适应理论和Lyapunov函数分析来设计控制器，使得系统全局稳定。然而刘献平［11］与 CHEN［9］将已知常数和未知频率的有界正弦函数视为外部干扰，这些形式的干扰基本上是由线性系统产生，与线性系统相比，非线性系统所产生的信号范围更广，其相较于线性系统接近于实际。SHUSTER［12］基于单位四元数法，在干扰系统是非线性的情况下，结合三乘二矩阵法的处理积，设计了依赖于外部信号控制器而不是依赖于外部信号的惯性矩阵控制器，但是外部信号和惯性矩阵是不确定的，此方法与实际理论相悖。因此，在此情况下，怎样解决更加接近于实际情况的外部干扰，以及怎样设计一个不依赖外部信号或者不依赖于矩阵惯性的控制器，其是一个富有挑战性的问题［13］。

本文对空间飞行器的飞行姿态这一关键参数采用了一个矩阵未知的Rodrigues参数加以描述。利用输出调节理论［14-19］，通过求解调节器方程，设计了外部非线性系统的非线性内部模型渐近估计。并且对控制器的状态进行了转换和控制器中使用的公式加以处理，给出了较合理Lyapunov函数，并设计了使飞机全局稳定的控制器。经过理论计算与仿真结果表明，此控制器设计是可行的。

1 空间飞行器姿态方程

描述姿态的参数有多种形式，本文采用Rodrigues参数［12］来描述飞行器的姿态，其定义如下:

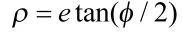
其中，e为欧拉转轴，φ为欧拉转角。

基于Rodrigues参数的飞行器姿态运动学方程为

空间飞行器的姿态动力方程［21］可以有下面的方程表示

针对所研究对象式（1）和式（2），在未知非线性系统式（3）的干扰与惯性矩阵不确定性扰动情况下，使用所设计的内部模型去预估不确定的外部模型系统，运用恰当的Lyapunov函数理论解算出未知的确定性与外在旋转矩阵干扰不相关的状态反馈控制器。所设计模型让任意初态与闭环系统的当前状态都是有界和满足的:

2 非线性内模设计

在内模设计之前，先看看下列方程

式（4）被称为调节器方程，（ρ（v），w（v），u（v））构成了相对于式（1）、式（2）和外部非线性系统式（3）调节器方程的解。

调节器对应的式（4）有未知解，其解是式（1）、式（2），并且外部系统式（3）全局稳定的输出调节问题有解的必要条件，此必要条件可由文献［14］得到。设 q（v）=0，可以得出 w（v）=0，u（v）=-R（v），ρ（v）能够产生多个解，令ρ（v）=0，即可解释此调节器的方程有解，得出式（1）、式（2）全局稳定性输出调节所产生的问题可以得出方程解。

设计系统预估的非线性内模，假设如下

假设 1［22］对于式（1）、式（2）和外部系统式（3），存在一个适当的侵入系统:

其中，θi表示状态变量，Fi、Gi、Ψi、Hi作为前提矩阵，用于描述系统有恰当的维数，并且矩阵对（Fi，H）i来说其是一组能够观测的矩阵对，从而函数可以得出如下的式子

定义的非线性函数，并满足:

因此，其确定有一个合适的矩阵K可以让F-KH是一个Hurwitz矩阵，并且存在两个适当的正定矩阵P、Q，满足下面的方程:

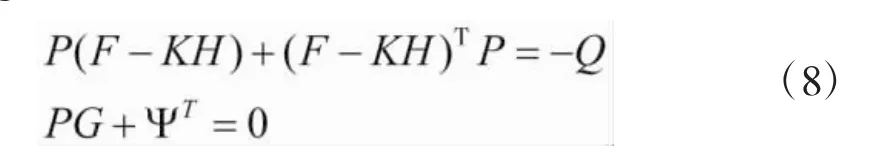
则可以设计一个用来处理外界干扰力矩的非线性内模式（9），

注1:在文献［22］中假设条件1首次被提出，且基于假设2，CHEN等人［23］解决了一类最小相位非线性系统的干扰问题。

3 状态变换

在控制器设计前，对内模作如下状态变换

可得

由式（10）可得

其中，

引理1［13］由改变能量函数技术可知，一定存在适当的实常数和光滑的正定函数

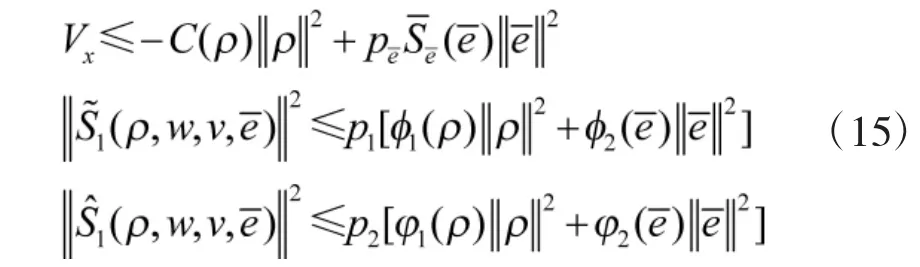
其中，光滑函数 C（ρ）＞0。

4 控制器设计

运用如下Lyapunov函数鲁棒性理论解决方法，利用此方法去解算控制器中闭环系统鲁棒性问题，能够得出如下所示的定理。

定理 1:以式（1）、式（2）与式（9）为研究对象，并且设式（1）满足其条件的前提下，转动惯量矩阵J其有不稳定的参数变量并且存在式（3）所得出的非线性干扰力矩的情况下，能够得出如下所示的控制器式子:

因此，实现了所描述的解决方法，证明如下。

证明 考虑下面Lyapunov函数

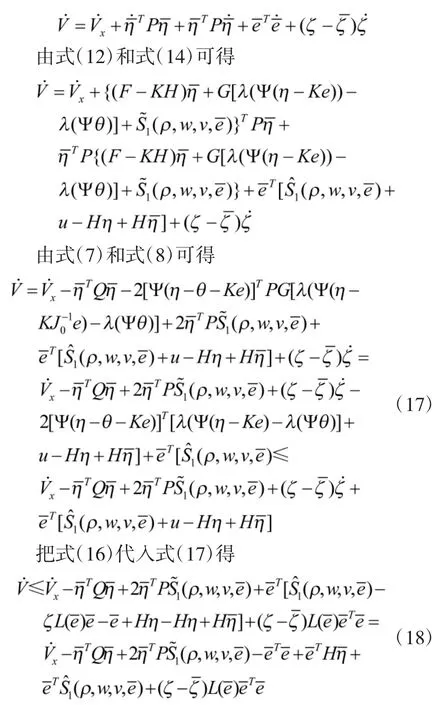
把式（15）中第 1个式子代入式（18），且进行Young不等式变换:对于任意的 ＞0，使得不等式

成立，从而得到

其中，σmi（nQ）是矩阵Q的最小特征值，为满足一定条件下的预计算的正常数的参数值。

对式（10）进行整理可得:

选取关于状态ρ的函数B（ρ），使得

由于J0正定，可知

实现了所需要求解问题的要求。证毕。

5 数值仿真

进行了系统的仿真实验，并验证了所提出的控制规律。

则让转动惯量与标称部分的矩阵如下所示，

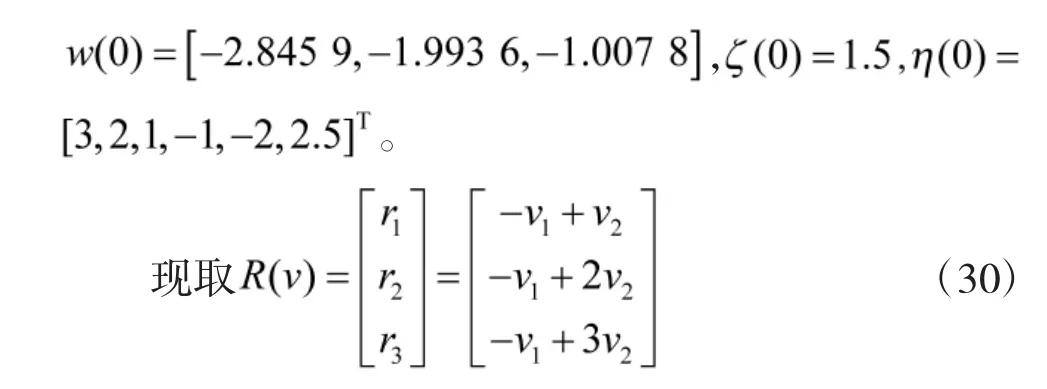
其中，v1，v2是由下面外部非线性干扰系统产生:

可知空间飞行器的姿态动力方程为

由式（1）、式（31）和式（32）可知，设 q（v）=0，则调解方程的解为

由内模设计部分知，取

可知以上3个都是Hurwitz的矩阵，说明满足理论要求和假设条件。

则非线性内模为

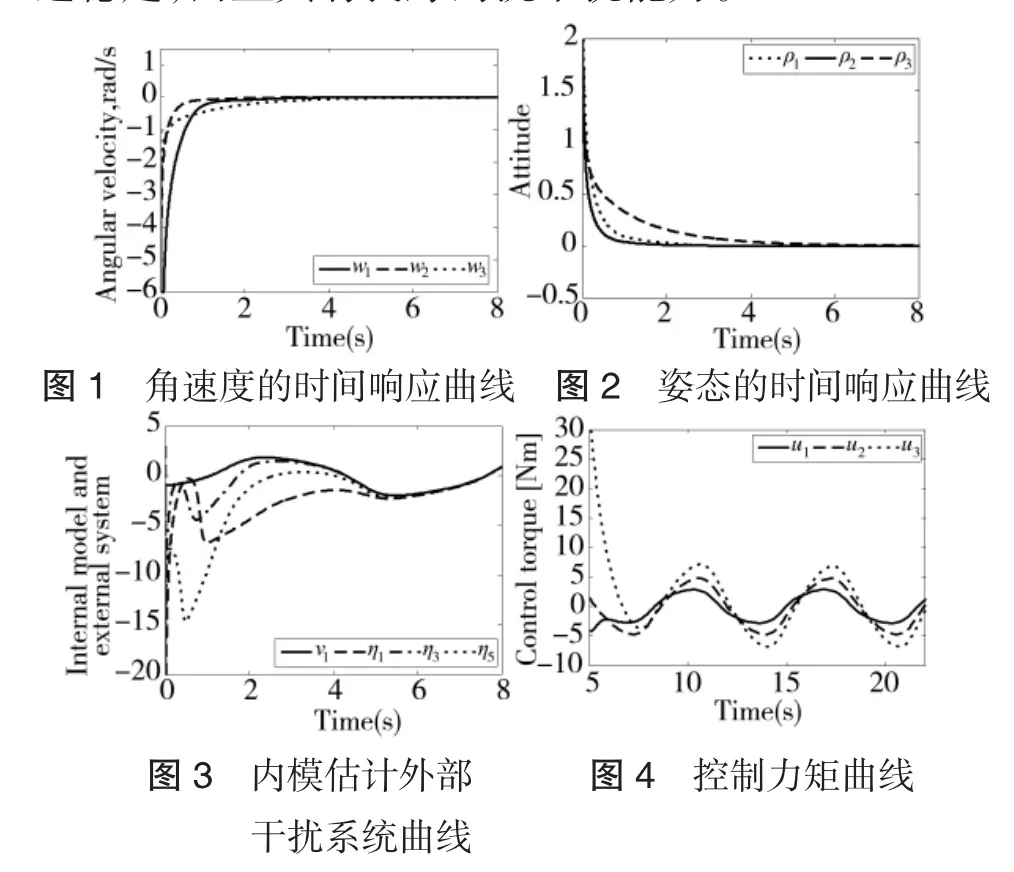
运用Matlab工具，其运行结果如下页图1～图4所示。图1曲线显示了空间飞行器的角速度的变化；图2曲线显示了空间飞行器的姿态所产生变化；图3曲线显示了所示设计的内部模型估计的外部系统的变化；图4为其控制扭矩曲线。

从仿真软件得出曲线结论可知，本文设计的控制律不仅能使刚体空间飞行器的姿态和角速度渐近稳定，而且具有良好的抗干扰能力。

6 结论

针对含有参数不确定和外部干扰信号的空间飞行器，采用Rodriguese参数描述的飞行器数学模型，设计了一个基于非线性内模的反馈控制器。并且证明了闭环系统的全局渐近稳定。仿真表明，本文提出的控制器具有针对空间飞行器的转动惯量参数不确定的良好鲁棒性与比较强的抗非线性外部系统产生的干扰能力，从而证明了控制器的有效性和可行性。