具有Holling IV型功能反应的分数阶捕食者-食饵模型的动力学分析

杜争光



具有Holling IV型功能反应的分数阶捕食者-食饵模型的动力学分析

杜争光

（陇南师范高等专科学校数学系，甘肃，成县 742500）

讨论了一类具有Holling IV型功能反应和Leslie-Gower数值反应的分数阶捕食者-食饵模型。利用分数阶微分系统的稳定性理论，给出了该系统在平衡点稳定的必要条件和充分条件。数值模拟也体现了分数阶微分系统的复杂性和丰富性。

分数阶；平衡点；稳定性；Holling IV型功能反应

0 引言

分数阶捕食者-食饵模型是一种重要的种群模型，受到诸多学者的青睐，并且已经取得了一系列成果[1-7]。田晶磊[3]对三种群分数阶捕食者-食饵模型进行了研究，给出了系统在平衡点稳定性的一系列结论。蒲武军[4]对一类分数阶的广义捕食者-食饵模型平衡点的稳定性进行了研究，得到了分数阶的捕食者-食饵系统在平衡点的稳定性与系统的阶有关系。刘永[8]对整数阶的广义Holling IV型捕食者-食饵模型做了研究，并指出，Holling IV型功能反应更符合实际：当食饵的数量超出临界值时，食饵会表现出一种“群体防御”性能，从而抑制捕食者数量的增加。

本文考虑一类食饵具有 Logistic 增长且带有Holling IV型功能反应函数，捕食者具有Lislie型数值反应的分数阶捕食者-食饵模型：

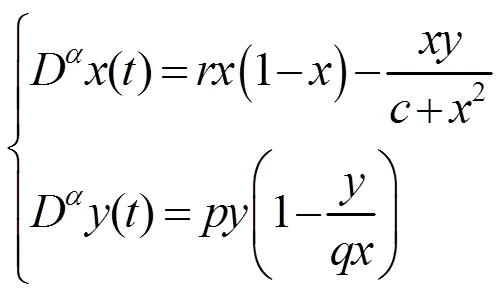
1 预备知识和引理

首先介绍Caputo分数阶导数的概念和性质。

性质[10]Caputo分数阶导数满足线性运算性：

下面给出分数阶微分系统在平衡点局部渐进稳定的一个结论。

设分数阶微分系统：

2 主要结果及其证明

这里主要讨论系统(1)在平衡点的局部渐进稳定性。在不引起混淆的情况下，后文所言稳定是指局部渐进稳定。

2.1 平衡点的存在性

进一步讨论平衡点的个数。方程(4)的正实根不仅与方程的系数有关，而且与其正极值点的符号有关，求出函数的导数：

2.2 平衡点的稳定性

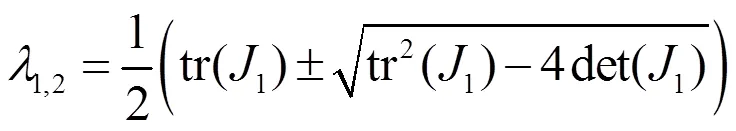
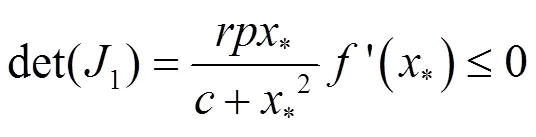
3 数值公式及模拟

在数值模拟时，需要对系统(1)的进行离散化处理，并采用它的迭代形式[3]。

一般地，分数阶微分系统:

与其等价的Volterra积分方程为：

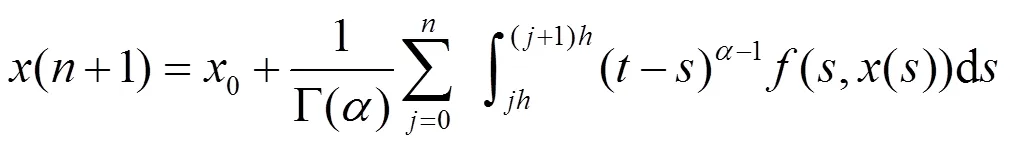
现利用上式对系统(1)离散化处理，并主要对于定理4的4.1 和4.2进行数值模拟。

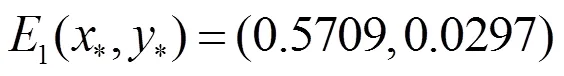
图1 平衡点E1的轨线，p = 0.065 , α =0.99

图2 平衡点E3的轨线， p = 0.11 , α=0.9

图3 平衡点E2的轨线，p = 0.065 , α=0.6

4 进一步讨论

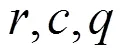
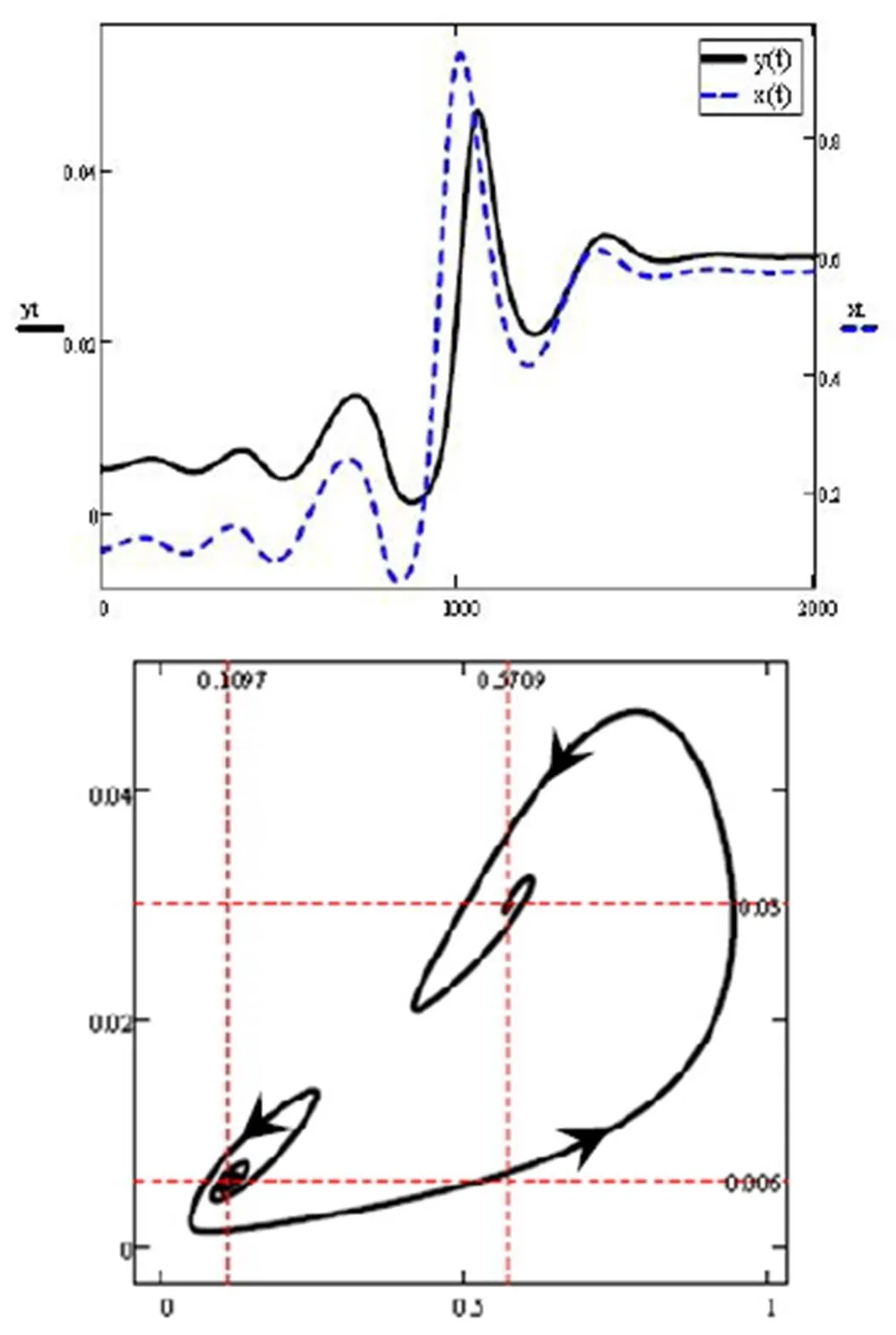
图4 平衡点E1的轨线， p = 0.17 , α= 1.27

以上数值模拟说明，分数阶导数的阶不仅影响系统收敛到平衡点的速度，还影响该系统的稳定性，也说明分数阶微分系统比整数阶微分系统更加复杂和丰富。

[1] Margarita Rivero, Juan J.rujillo, Luis Vázquez. Fractional dynamics of populations [J]. Applied Mathematics and Computation，2011,218:1089-1095.

[2] 王虎,田晶磊,孙玉琴,等. 具有阶段结构的时滞分数阶捕食者-食饵系统的稳定性分析[J].应用数学学报,2018, 41(1):27-42.

[3] 田晶磊. 分数阶捕食者—食饵系统的动力学研究[D].北京:北京交通大学,2015.

[4] 蒲武军,杜争光. 一类分数阶广义捕食者-食饵模型的动力学分析[J].西北师范大学学报:自然科学版,2018, 54(5):10-15.

[5] George Maria Selvam A, Janagaraj R, Dhineshbabu R. Fractional Order Nonlinear Prey Predator Interactions [J]. International Journal of Computational and Applied Mathematics, 2017,12:495-502.

[6] Cruz Vargas-De-Leon, Volterra–type Lyapunov functions for fractional-order epidemic systems[J]. Communications in Nonlinear Science and Numerical Simulation,2015,24: 75-85.

[7] Moustafa El-Shahed1, Ahmed A M, Ibrahim Abdelstar M E. Fractional Order Model in Generalist Predator-Prey Dynamics[J]. International Journal of Mathematics And its Applications, 2016(4):19-28.

[8] 刘永. 广义Holling Ⅳ型食饵捕食者模型的动力学性质分析[D].武汉:武汉理工大学,2017.

[9] 赵莹莹. 分数阶微积分的若干理论及应用[D].郑州:郑州大学,2013:13-22.

[10] 吴强,黄建华. 分数阶微积分[M].北京:清华大学出版社,2017:74-87.

[11] Podlubny I. Fractional Differential Equations[M]. London: Academic Press,1999.

DYNAMICAL ANALYSIS OF A FRACTIONAL-ORDER PREDATOR-PREY MODEL WITH HOLLING IV FUNCTIONAL RESPONSE

DU Zheng-guang

(Department of Mathematics，Longnan Teachers College, Chengxian, Gansu 742500,China)

A fractional-order predator-prey model with Holling IV functional response and Leslie-Gower type numerical responses is investigated. By applying the stability theory of fractional-orderdifferential systems, we give some necessary conditions and sufficient conditions for the stability of the equilibrium point. Moreover, the numerical simulation also shows that the complexity and richness of the fractional-order differential systems.

Fractional-Order；Stability；Equilibrium Point；Holling IV Functional Response

1674-8085(2019)03-0009-05

O157.13

A

10.3969/j.issn.1674-8085.2019.03.002

2019-02-21；

2019-03-12

杜争光((1973-），男，甘肃礼县人，副教授，主要从事应用微分方程研究(Email:lnsz_dzg@163.com).