二硫化碳-四氯化碳物系的物性方法筛选与过程模拟
2019-06-13李大孟刘朝义连明磊
李大孟,方 清,刘朝义,李 静,连明磊,叶 昆
(1.六盘水师范学院化学与材料工程学院,贵州 六盘水 553004; 2.中国石油工程建设有限公司华北分公司,河北 任丘 062552)
1 引言
二硫化碳是重要的化工原料,其沸点为46.5℃,是用于制造黏胶纤维、玻璃、人造丝等的原料[1-5]。四氯化碳的沸点为76.8℃[6],是用于生产氟里昂和织物干洗剂的化工原料,还能用作于溶剂、灭火剂、有机物氯化剂、香料浸出剂、纤维脱脂剂、药物萃取剂等[7-9]。二者在很多工艺中均会混合,若不将其分离回收则会造成浪费和污染环境,这在化工生产中是不经济和不可取的。因此要求这两者完全脱除并且达到回收再利用。
本文以二硫化碳-四氯化碳混合物物系为研究对象,通过Aspen Plus软件对该体系的气液相平衡数据分别进行WILSON、NRTL及UNIQUAC热力学模型的计算,选出最优的物性方法,同时运用化工模拟软件Aspen Plus中的Sensitivity功能,考察全塔理论板数、回流比、原料进料位置对二硫化碳质量纯度的影响。
2 物性方法比选
本文分别使用WILSON、NRTL及UNIQUAC三种热力学模型拟合二硫化碳-四氯化碳物系气液相平衡数据,以Hlavaty,K等人[10]所报道的实验数据为依据,对二硫化碳-四氯化碳体系的压力和平衡气相组成进行计算,并将其与实验数据进行对比,筛选出最佳的物性方法。
2.1 WILSON模型
经WILSON热力学模型计算得出二硫化碳-四氯化碳的压力与平衡气相组成详见表1、表2。

表1 二硫化碳-四氯化碳体系压力的计算值与实验值的对比表(WILSON方程)
由表1得二硫化碳-四氯化碳体系压力的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0002, 0.00009;最大相对偏差和平均相对偏差分别为0.04249%, 0.0161%。
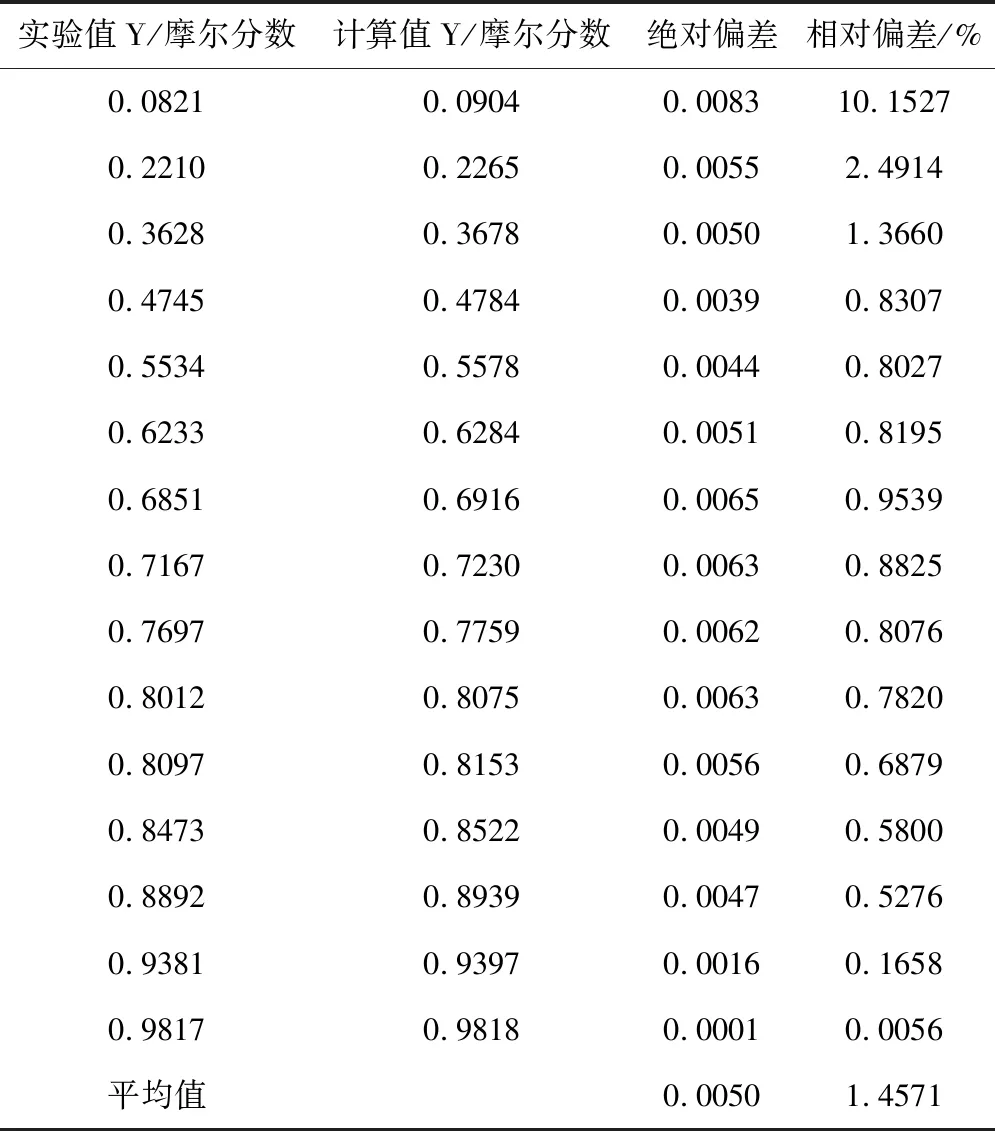
表2 二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的对比表(WILSON方程)
由表2得二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0083, 0.0050;最大相对偏差和平均相对偏差分别为10.1527%, 1.4571%。
2.2 NRTL热力学模型
经NRTL热力学模型计算得出二硫化碳-四氯化碳的压力与平衡气相组成详见表3、表4。

表3 二硫化碳-四氯化碳体系的压力计算值与实验值的对比表(NRTL方程)
由表3得二硫化碳-四氯化碳体系压力的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0002, 0.0001;最大相对偏差和平均相对偏差分别为0.0389%,0.0141%。

表4 二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的对比表(NRTL方程)
由表4得二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0078, 0.0052;最大相对偏差和平均相对偏差分别为9.004%, 1.4011%。
2.3 UNIQUAC热力学模型
经UNIQUAC热力学模型计算得出二硫化碳-四氯化碳的压力与平衡时的气相组成详见表5、表6。

表5 二硫化碳-四氯化碳的压力计算值与实验值的对比表(UNIQUAC方程)
由表5得二硫化碳-四氯化碳体系压力的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0002, 0.00009;最大相对偏差和平均相对偏差分别为0.0436%,0.016%。

表6 二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的对比表(UNIQUAC方程)
由表6得二硫化碳-四氯化碳体系平衡气相组成的计算值与实验值的最大绝对偏差和平均绝对偏差分别为0.0083, 0.0050;最大相对偏差和平均相对偏差分别为10.0938%,1.4547%。
3 热力学模型比选
二硫化碳-四氯化碳体系的气液相平衡实验数据经三种热力学模型计算后并进行对比,所得的相应误差分析见表7,综合比较得出NRTL模型为最优;并将NRTL模型拟合的曲线与实验数据点进行比较,作图于图1中。

表7 3种热力学模型的误差分析

其中,P-压力,y-气相中二硫化碳的摩尔分数,N-实验点数,exp-实验值,cal-计算值。

图1 NRTL模型P-xy计算值与实验值的比较
4 工艺流程优化
本文通过运用化工模拟软件Aspen Plus的Sensitivity功能,考察全塔理论板数、回流比、原料进料位置对二硫化碳质量纯度的影响并对塔径进行计算。进料条件见表8。

表8 进料条件
4.1 全塔理论板数对二硫化碳的质量纯度的影响
本文考察了不同全塔理论板数对二硫化碳质量纯度的影响,其计算结果见表9。
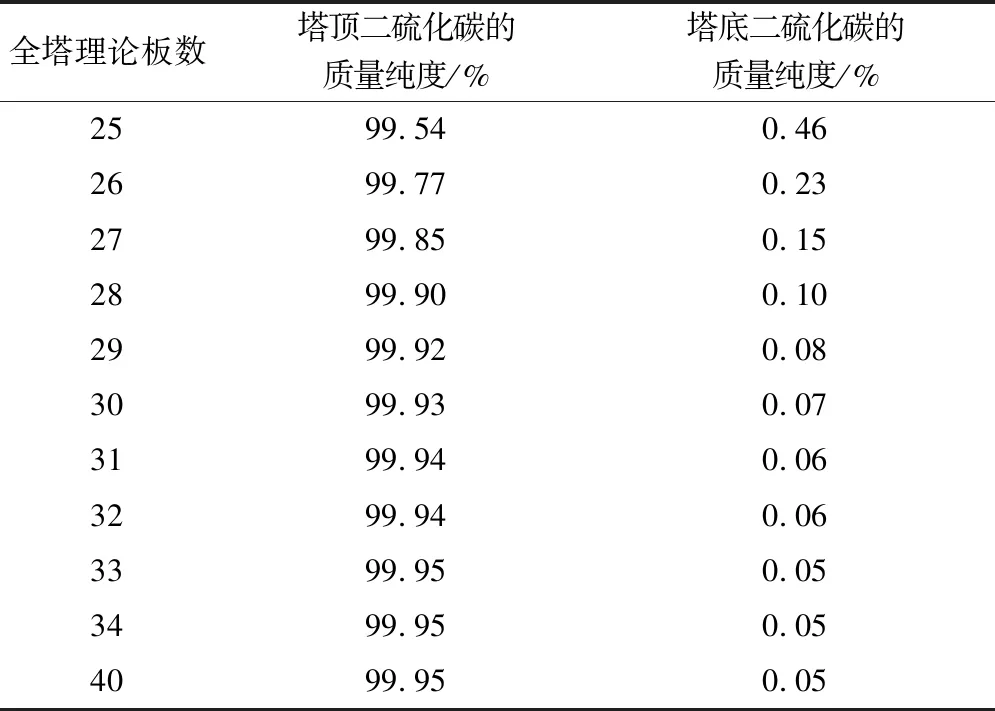
表9 全塔理论板数对二硫化碳质量纯度的影响
由表9可得出:二硫化碳的质量纯度随塔板数的增加而提高,当塔板数为33时,二硫化碳的质量纯度增加到99.95%,并且当全塔理论板数继续增加,二硫化碳的质量纯度维持此值不再改变,因此,全塔理论板数选33块较为合理。
4.2 回流比对二硫化碳质量纯度的影响
本文考察了不同的回流比对二硫化碳质量纯度的影响,计算结果见表10。

表10 回流比对二硫化碳质量纯度的影响
从表10中得出:塔顶二硫化碳质量分数随回流比的增加基本不变的趋势,可得出当全塔理论板数达到33时,很小的回流比就可使二硫化碳的质量纯度达到99.95%。因此,回流比选0.3。
4.3 原料进料位置对二硫化碳的质量纯度的影响
本文考察了不同原料进料位置对二硫化碳的质量纯度的影响,计算结果列举于表11中。

表11 原料进料位置对二硫化碳纯度的影响
从表11中得出:原料的进料位置为第24块塔板时,二硫化碳的质量分数最高,达到99.97%,因此,原料进料位置选第24块。
4.4 塔径的计算
本文通过Aspen Plus软件计算了不同塔板数上的塔径,见表12。

表12 塔板数上的塔径和塔盘面积
由表12可知,最大的塔径出现在第30至32块塔板上,对应的塔盘面积为0.11m2,塔径计算值为0.37m。
4.5 各塔板的温度和二硫化碳的气液质量组成分布
本文考察了不同塔板数上的温度和二硫化碳的气液质量组成,计算结果见表13。
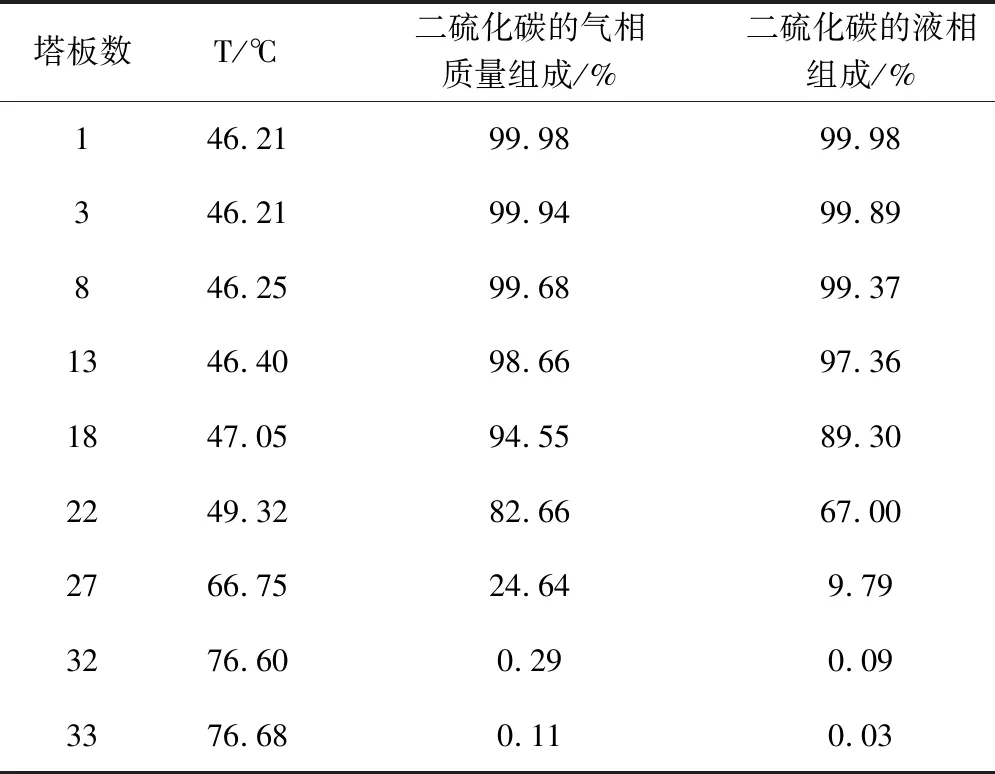
表13 各塔板的温度和二硫化碳的气液质量组成
由表13得出,在第1块塔板上二硫化碳的气相质量组成为99.98%,在第33块塔板上二硫化碳的液相组成为0.03%,因此,二硫化碳与四氯化碳混合物得到了较好的分离。
5 结论
(1)本文运用化工模拟软件Aspen Plus中的Data Regression功能,分别采用WILSON、NRTL及UNIQUAC三种热力学模型进行计算和分析气液相平衡实验数据,选出NRTL为最佳物性方法。
(2)通过工艺流程优化,运用NRTL物性方程对分离二硫化碳-四氯化碳混合物的过程进行模拟,得出当全塔理论板数为33块,回流比为0.3,原料进料位置为第24块时,二硫化碳的质量纯度达到99.98%,以上结果为二硫化碳-四氯化碳混合物的分离工艺的设计提供了理论与技术参考。
