四旋翼直升机的线性自抗扰与非线性H2/H∞混合控制

刘俊杰，高强，孙明玮，陈增强

(1.南开大学 人工智能学院，天津，300350；2.天津理工大学 电气与电子工程学院，天津，300384)

无人机(unmanned aerial vehicle，UAV)也称“无人飞行器”，即不搭载飞行员的空中飞行器[1]。近年来，随着科学技术尤其是传感器技术和控制理论的不断提高[2]， 无人飞行器的发展在自动控制领域引起了人们的高度关注。多种无人飞行器已经被用于执行各类任务，如地面监测、高空航拍、抗震救灾、军事侦察等[3]，因此，开展具有垂直起降功能的高机动性、强稳定性的无人飞行器控制研究在空中机器人领域意义重大。作为一种典型的垂直起降无人飞行器，四旋翼无人直升机结构简单，通过2对旋翼产生的平衡力实现稳定悬停和改变飞行状态，并能完成低速飞行等动作[4]。然而，四旋翼直升机的控制量数目少于系统的自由度，属于欠驱动系统，在实际飞行过程中受诸多因素影响，是一个非线性强、参数不确定、耦合强、对外扰敏感的复杂对象，其跟踪控制问题成为控制领域的难点和热点。针对简化的四旋翼直升机模型，常见的线性算法有PID控制[5-6]、LQR控制[7]以及线性H∞控制[8]。由于四旋翼直升机模型中的强非线性，且在飞行过程中易受非线性阻力的影响，当飞行器远离平衡点时，线性控制算法可能失效，因此，研究人员使用反步法[9-10]、反馈线性化[11]、滑模控制[12]、浸入和不变控制[13]以及非线性 H∞控制[14]等非线性控制方法进行控制器设计。针对拉格朗日-欧拉方程推导的非线性模型，RAFFO等[14]采用反步法和H∞控制对四旋翼直升机系统中的持续外部扰动进行抑制。MOKHTAR 等[15]考虑四旋翼直升机非线性模型的不确定性，设计非线性H∞输出反馈控制器，并采用高阶滑模观测器进行扰动估计。RAFFO 等[16]提出一种非线性鲁棒控制结构，将四旋翼直升机系统划分为旋转运动子系统和平移运动子系统，并采用非线性H∞控制器对旋转运动进行镇定，利用模型预测控制实现位置坐标的跟踪控制。自抗扰控制(active disturbance rejection control，ADRC)是韩京清[17]提出的一种新型实用控制技术，其不依赖系统的精确模型，可直接利用被控对象的输入输出信息对系统状态以及“总扰动”进行估计并在线补偿[18]。在此基础上，GAO[19]将非线性自抗扰控制器中的非线性环节进行线性化处理，极大简化了ADRC的参数整定方法。目前，自抗扰控制已逐步应用于各个领域，如工业过程[20]、伺服系统[21]、机器人控制[22]等。本文作者针对四旋翼直升机的非线性模型，将其划分为旋转运动子系统与平移运动子系统，在考虑持续外部扰动的情况下，利用线性自抗扰控制解决平移运动中系统位置坐标的跟踪问题；对于四旋翼直升机的旋转运动，采用一种非线性H2/H∞混合控制方法，在抑制外部干扰的同时保持良好的跟踪性能。

1 系统模型

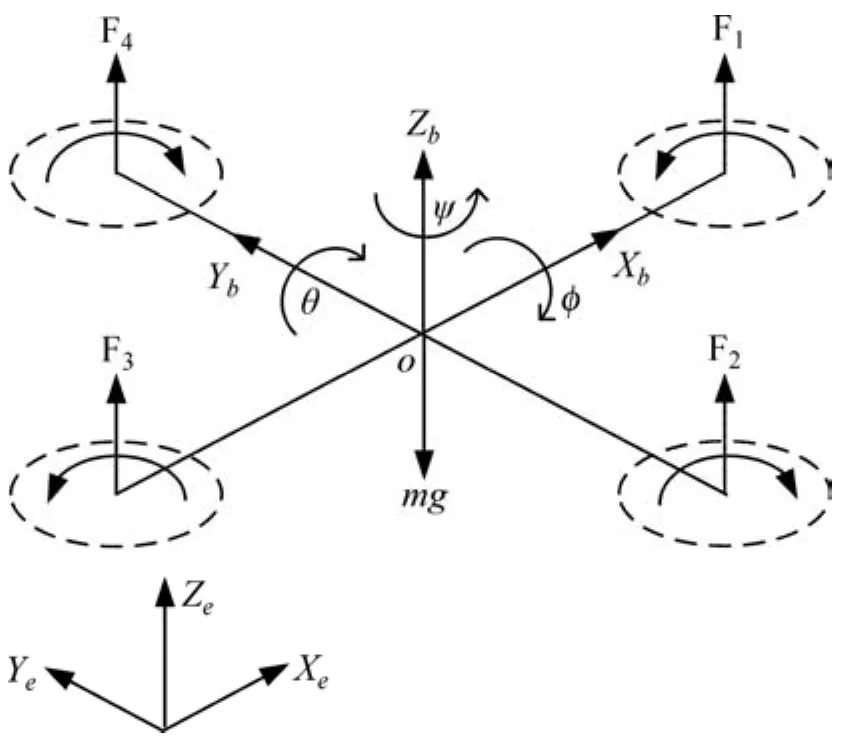
图1 坐标系示意图Fig.1 Diagram of coordinate system

坐标系示意图如图1所示，四旋翼直升机具有6个自由度。图1中：Xe=[x,y,z]T，η=[φ,θ,ψ]T，分别表示四旋翼直升机在惯性坐标系中的位置和姿态角(滚转、俯仰和偏航)；，表示机体坐标系；Xb轴指向飞机前进方向；YbXb正交；Zb垂直于XbOYb并指向上方；地面坐标系为惯性坐标系；姿态角，表示机体坐标系与地面坐标系之间的旋转关系。考虑到右手坐标系，由绕x，y和z轴的旋转关系可以得到从机体坐标系到地面坐标系的转换矩阵Rb为

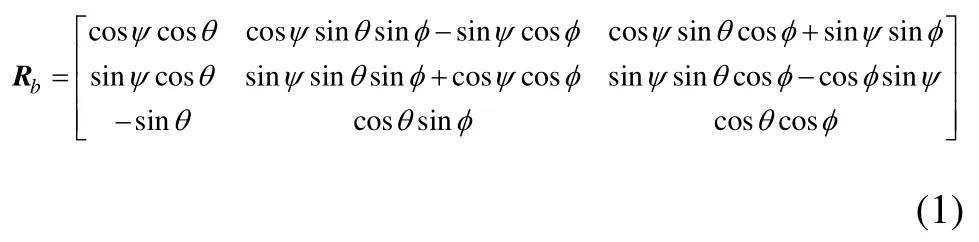
其中：

利用基于动能和势能的拉格朗日-欧拉方程，可将四旋翼无人飞行器的运动方程表示为[17]

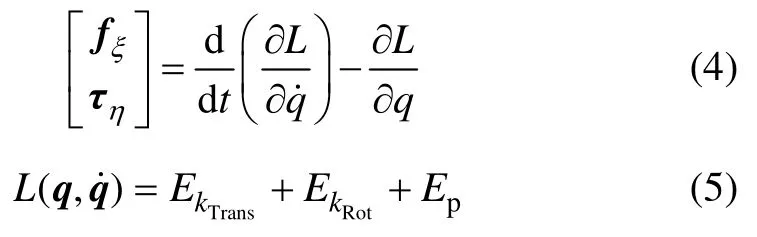
其中：L为四旋翼无人飞行器模型的拉格朗日算子；EkTrans为平移运动动能；EkRot为旋转运动动能；Ep为系统总势能。

即

其中：m为机体质量；g为重力加速度；为外部扰动。

定义矩阵N为以下形式：

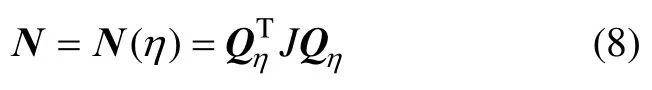
其中：J=diag(Ixx,Iyy,Izz)，为转动惯量矩阵。则旋转动能方程可以表示为

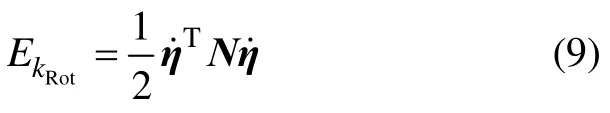
令M(η)=Ν(η)，拉格朗日-欧拉旋转方程可以重新表示为

其中：

因此，利用拉格朗日-欧拉方程导出的四旋翼直升机旋转运动的非线性数学模型为

故四旋翼无人直升机的非线性数学模型为

2 控制策略

由四旋翼直升机动力学模型可知，飞行器在飞行过程中控制器直接作用于飞行器姿态角与高度，姿态角又直接影响飞行器的水平位置，因此，飞行控制器多采用内外环的结构。考虑四旋翼无人直升机的参数不确定、未建模动态及外部扰动，设计一种非线性鲁棒控制策略，以实现其路径跟踪控制，其控制结构如图2所示。式(13)将四旋翼直升机系统分为旋转运动和平动运动，为解决四旋翼直升机旋转运动控制问题，控制结构内环采用一种非线性混合控制方法，在考虑参数不确定性和持续外部扰动的情况下，实现姿态角和姿态角速度的稳定控制。对于平移运动，在控制结构外环采用线性自抗扰控制器，实现四旋翼直升机位置的轨迹跟踪控制。位置参考信号由参考路径发生器产生，当考虑未建模动态和持续外部扰动时，对所设计的线性自抗扰控制器进行总扰动估计并给予补偿。

2.1 旋转运动子系统控制

根据式(13)，在考虑扰动的情况下，四旋翼无人直升机的旋转运动方程为

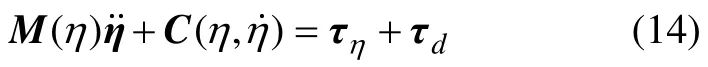
定义跟踪误差：

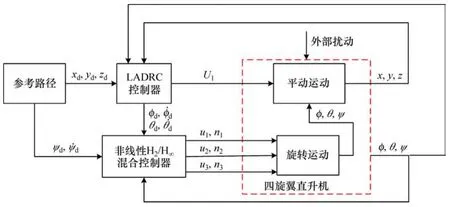
图2 控制结构Fig.2 Control structure

定义T矩阵形式如下：

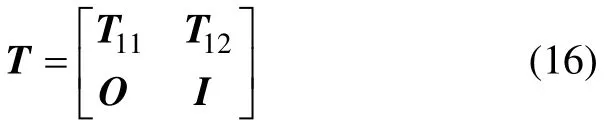
其中：T11=aI3×3,T12=bI3×3；a和b为待定正数；O和I分别为3阶零矩阵和单位矩阵。

由式(14)和式(15)可以推导出基于误差的状态空间表达式：

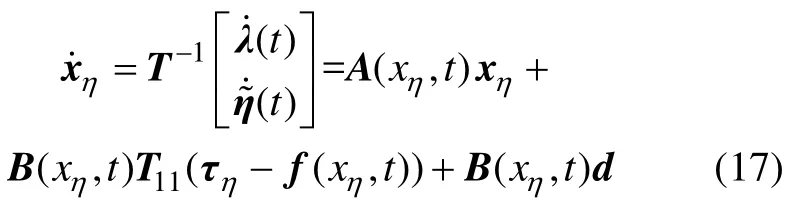
其中：

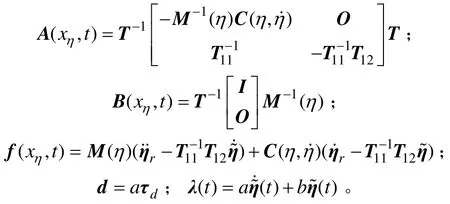
对于该旋转子系统，可设计如下控制律：

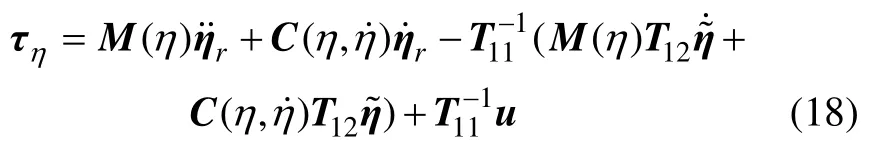
则基于状态误差的四旋翼直升机旋转运动方程可以重新表达为

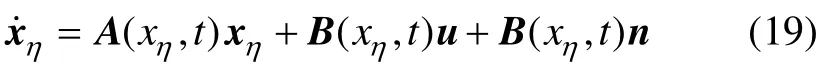
其中：u为控制输入；n为外部扰动。

对于具有参数不确定和外部扰动的四旋翼旋转运动系统，在有权矩阵Q1，Q1f，Q2，Q2f，R1，R2和P全部为对称正定矩阵，γ+∈R 的条件下，若控制器能在H∞扰动估计最大范围内，

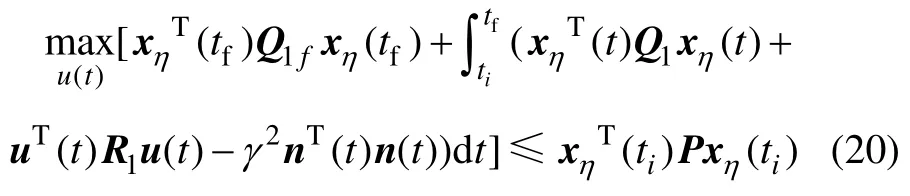
满足H2最优跟踪控制

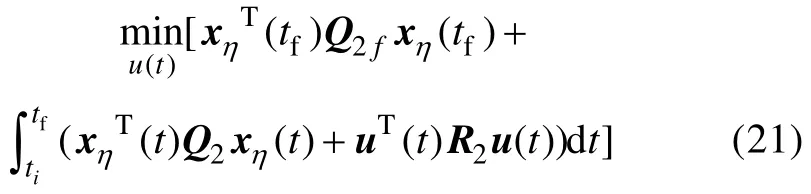
则可设计H2/H∞混合控制器，实现其稳定控制(其中，ti和tf表示控制的初始和最终时刻)。定义2个性能指标如下：

即需要满足的条件为

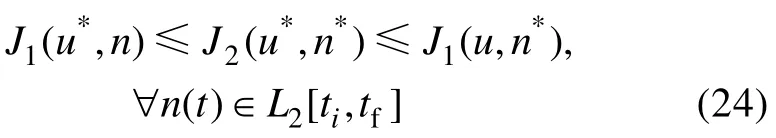
其中：u*和n*分别代表最优控制输入和最坏的扰动情形。

定理1[23]：对于式(19)中的误差状态系统，最优控制和最坏扰动可以分别选择以下形式：

其中：P1(xη,t)和P2(xη,t)为耦合非线性时变Riccati形式方程的解，具体形式参考文献[23]。

若选择P1(xη(tf),tf)=Q1f和P2(xη(tf),tf)=Q2f，代入式(25)和(26)，则式(25)和(26)就成为式(24)中H2/H∞混合控制最优跟踪问题的解。

定理2：若R1，R2和R定义为

选取Q1和Q2为

其中：Q11=q11I；Q22=q22I；q11＞0；q22＞0。

非线性时变Riccati形式方程解为

转换矩阵T选择如下形式：

参数a和b分别为：

2.2 平移运动子系统控制

其 中 ：uz=cosφcosθ,ux=cosψsinθcosφ+sinψsinφ,uy=sinψsinθ- cosψsinφ。

2.2.1 高度控制

以高度控制为例，设计自抗扰控制器，使得输出能够快速稳定跟踪设定值。考虑高度系统如下：

令x3=f1作为高度通道的扩张状态，且其导数为h1，则式(32)所示系统可以扩张为

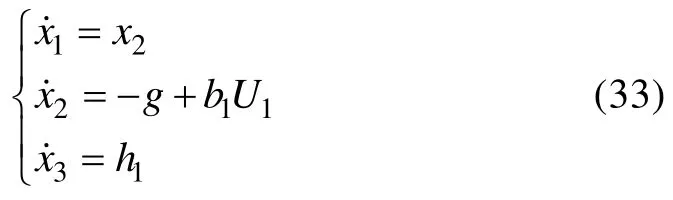
其中：x1=z表示高度；U1为控制输入。

式(33)对应的扩张状态观测器设计为

其中：zi(i=1，2，3)为状态xi(i=1，2，3)的估计值；βi(i=1，2，3)为观测器增益，为可调参数，且，；ωo1为观测器带宽。

控制律及补偿部分为：

2.2.2 横纵向运动控制

对于四旋翼的纵向运动和横向运动，设计线性自抗扰控制器时，设计控制律u0i(i=1，2)，补偿总扰动后，获得相应通道和扩张状态观测器的控制输入，ux，uy分别表示纵向运动和横向运动通道的虚拟控制律，与姿态角设定值θd和φd的关系为

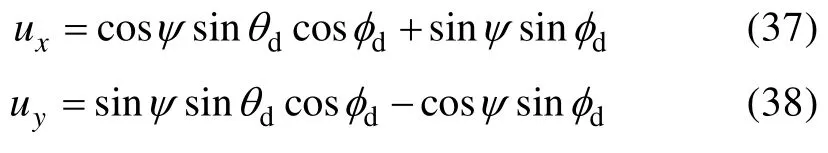
四旋翼的纵向运动的状态空间表达式为

令x6=f2作为纵向运动通道的扩张状态，且其导数为h2，则式(39)所示系统可以扩张为

式(40)对应的扩张状态观测器可设计为

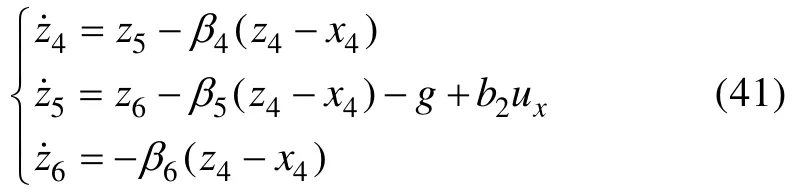
其中：zi(i=4，5，6)是状态xi(i=4，5，6)的估计值；βi(i=4，5，6)为观测器增益，为可调参数，且；ωo2为观测器带宽。

相对应的控制律可以选择为

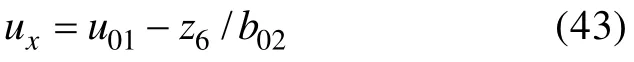
对于飞行器的横向运动，其状态空间表达式为

同理，可得如下四旋翼无人飞行器横向运动的控制器设计：

其中：zi(i=7，8，9)为横向通道状态及总扰动的估计值；βi(i=7，8，9)为观测器增益；b03为可调参数；；ωo3为观测器带宽；u02为误差控制律，控制器增益；ωc3为控制器带宽；yd为侧向移动设定值。

3 仿真结果

仿真中，选取四旋翼无人直升机的物理参数为机体质量m=2.85 kg，桨距l=0.197 m，x，y和z轴转动惯量分别为Ixx=Iyy=0.055 2 kg·m2和，重力加速度g=9.81 m/s2。参考路径设定为：x坐标变化设定值，y坐标变化设定值，z坐标变化设定值，偏航角设定值；飞行器的初始位置设定为(x，y，z)=(0，0，0)m，初始姿态角设定为(φ，θ，ψ)=(0，0，0)rad。在位置和姿态输出通道中分别添加白噪声扰动，功率为10-7。在仿真过程中，考虑参数的不确定性，对惯性参数上下浮动20%后，进行仿真并比较结果。其中，非线性混合H2/H∞控制器参数被整定为：γ=1，σ=0.5，q22=1；LADRC 控制器参数整定为：b01=1，b02=0.9，b03=0.9，ωo1=40，ωc1=150，ωo2=10，ωc2=5，ωo3=10，ωc3=5。

白噪声扰动下路径跟踪效果如图3所示。四旋翼直升机从初始位置(x，y，z)=(0，0，0)m开始，沿设定路径进行飞行，参考路径起点为(x，y，z)=(0，0，1)m，利用持续的白噪声信号干扰来模拟实际飞行产生的测量误差和外部干扰等因素，因此，在仿真结果中，系统输出存在不同程度的波动。从图3可以看出：四旋翼直升机轨迹能够较好地在较短时间内到达预期设定值，并较好地按照预设路线飞行；在对标称惯性参数进行20%上下浮动时，飞行轨迹没有发生较大变化，说明系统具有较强的鲁棒性。

图3 白噪声扰动下路径跟踪效果Fig.3 Path tracking under white noise disturbance

图4 白噪声扰动下位置坐标变化Fig.4 Position coordinates under white noise disturbance

图5 白噪声扰动下位置跟踪误差Fig.5 Attitude angle tracking error under white noise disturbance

图6 白噪声扰动下姿态角变化Fig.6 Attitude angle under white noise disturbance

四旋翼直升机在运动中位置坐标x，y和z的变化过程见图4。坐标x在大约2 s能够迅速跟上设定值，响应速度较快，y和z均能较好地稳定跟踪预设值。白噪声扰动下位置跟踪误差见图5。从图5可以看出：对模型中标称惯性参数进行20%上下浮动，控制器参数保持不变，系统输出依然能够保持较小的跟踪误差，说明所采用的控制器对四旋翼直升机的参数不确定性具有较强的鲁棒性。图6所示为四旋翼直升机旋转运动中各姿态角的变化情况。从图6可见：在自噪声干扰下，滚转角φ和俯仰角θ能够较平稳地变化；偏航角ψ在大约2 s达到设定值，尽管产生一定的超调量，但能够迅速到达稳定设定值并保持不变，在惯性参数进行±20%变化时，仍然可以保持较好的控制效果。

4 结论

1)针对四旋翼直升机的轨迹跟踪问题，设计了一种线性自抗扰与非线性 H2/H∞混合控制结合的控制策略。首先，基于拉格朗日-欧拉方程获得四旋翼直升机的强非线性数学模型。在此基础上，将位置系统中的未知扰动作为系统的扩张状态，并设计相应的线性自抗扰控制器；针对姿态的稳定跟踪控制问题，采用了一种非线性 H2/H∞混合控制方法，能够使外扰衰减的同时保持良好的H2跟踪性能。

2)本文所设计的四旋翼直升机稳定控制算法能够较好地抑制系统参数不确定性和外部扰动的影响，具有响应速度快、鲁棒性强等优点。