多轴车辆轮桥加载试验台的解耦控制实验研究

王慧，赵国超，金鑫

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新，123000;2.哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨,150001)

随着对车辆安全可靠性和运行性能要求的不断提高，车辆关键部件的模拟加载试验研究越来越受到重视[1–2]。车辆的安全可靠性和运行性能在很大程度上取决于车辆发动机和轮桥的工作特性，而车辆发动机往往是既定的按需选型产品，因此，合理设计车辆轮边和传动桥并进行各种复杂工况下的模拟加载试验至关重要[3]。作为一类用于特殊作业的重型车辆，其传动桥多为四轴或多轴输出，工况更为复杂，因此，对多轴车辆传动桥以及轮边的模拟加载试验尤为重要[4–5]。传统轮桥加载试验台可完成相对简易的单项试验，但存在功耗大、效率低等缺陷[6]。对于相对复杂的综合试验，可采用电封闭加载试验台来实现，但所需电器设备庞大，且电网形式的能量回收存在冲击和电污染现象，极易出现元器件毁坏等问题[7]。基于二次调节的模拟加载试验台[8–9]在模拟传动桥实际工况的加载方面具有较高的可靠性和可控性，且价格相对低廉。尤其在动态模拟加载方面，此类试验台具有明显优势[10]，能量回收效果显著，与普通的液压节流加载相比，可节能30%以上[11]。但二次调节加载试验台模拟驱动的转速控制系统和模拟加载的转矩控制系统通过恒压油源网络和机械传动轴系耦联在一起[12]，使得转速和转矩控制系统存在严重的耦合干扰问题[13]，造成试验台动态模拟加载稳定性和准确性下降[14–15]。本文作者针对基于二次调节的模拟加载试验台，建立二次调节轮桥传递函数模型及实验现场，求解出对角矩阵，并利用对角矩阵对系统进行解耦控制，最后通过耦合干扰实验及解耦控制实验，得到耦合干扰的规律，确定解耦控制方法的有效性，提高试验台的可控性和可靠性。

1 多轴车辆轮桥模拟加载试验台

以特种作业的4轴重型卡车为原型，其传动轴系包括驱动输入轴、轮边(左、右)输出轴和二次输出轴，搭建的模拟加载试验台组成如图1所示。由图1可见：试验台主要包括恒压油源、驱动单元、二次输出和轮边加载单元、传动桥和计算机控制系统。驱动和加载各单元的核心是二次元件(4组)，其液压口通过液体压力耦合并联于恒压油源提供的恒压网络上，机械口通过转速转矩传感器、变速器、传动桥和轮边等机械耦合联接在一起[16–17]。试验台的功能是对驱动转速和输出转矩进行调节，实现对传动桥及轮边的驱动和输出转矩进行模拟。1号二次元件模拟车辆发动机驱动转速，2号二次元件模拟传动桥二次输出转矩，3号和4号二次元件分别模拟左右轮边输出转矩。系统工作时，1号二次元件（马达工况）将来自恒压油源的液压能转换成机械能，并通过传动桥输入给2号、3号和4号二次元件（泵工况），实现对传动桥的加载。与此同时，2号、3号和4号二次元件又将输入的机械能转换为液压能，重新回馈给1号二次元件（马达），从而形成1个闭式循环的功率流[18]，实现能量回收。由于系统是通过机械耦合与液压耦合2种连接形式组成的，因此，驱动单元的压力波动会通过液压网络影响轮边输出单元和二次输出单元的压力，同时，输出单元的压力波动又会影响到驱动单元的压力，此种耦合形式为液压耦合；模拟4个轴系的元件通过联轴器、传感器、变速器等环节直接与加载传动桥联接，构成四轴机械传动系统，每个单元的负载敏感系数存在差异，因此，造成驱动单元与输出单元存在较强的耦合干扰，某个单元出现波动都会对其他单元造成不同程度的影响，从而影响整个试验台的加载性能，此种耦合形式为机械耦合。

2 二次调节试验台加载系统建模

针对图1所示加载试验台，根据二次元件、阀控变量液压缸[19]、传动桥等的结构和工作原理，建立加载系统各环节的数学模型如下。

二次元件前置级排量控制的电液伺服阀流量方程为

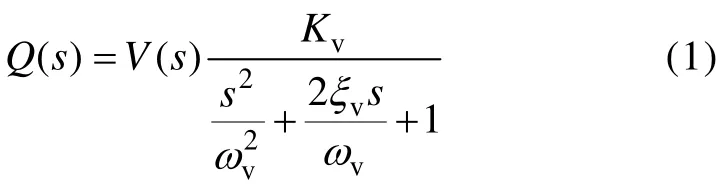
式中：Q(s)为阀输出流量，m3/s；V(s)为的输入电压，V；Kv为的流量补偿系数，m3/(s·V)；ωv为阀的固有频率，Hz；ξv为阀的阻尼比。

变量液压缸流量平衡方程为

式中：qvi为变量液压缸流量，m3/s；yi为变量液压缸活塞位移，m；Agi为变量液压缸有效作用面积，m2；Cti为变量液压缸泄漏系数，m3/(s·Pa)；pLi为变量液压缸负载压力，Pa；Vti为变量液压缸总容积，m3；βe为液压油体积弹性模量，N/m2；i为变量液压缸标号，i=1，2，3，4。

变量液压缸力平衡方程为

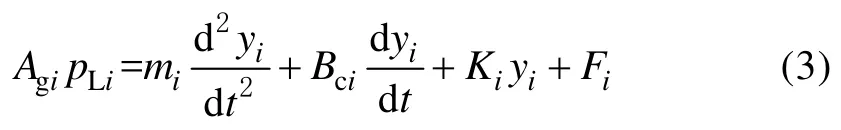
式中：mi为变量液压缸等效质量，kg；Bci为变量液压缸阻尼系数，N·s/m；Ki为负载弹簧刚度，N/m；Fi为变量液压缸外负载力，N。

图1 轮桥加载试验台组成Fig.1 Composition of loading test bench for wheel-bridge

二次元件排量方程为

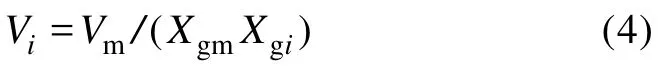
式中：Vi为二次元件排量，m3/rad；Vm为二次元件最大排量，m3/rad；Xgm为液压缸活塞最大行程，m；Xgi为第i个液压缸活塞行程，m。

驱动单元二次元件力矩平衡方程为

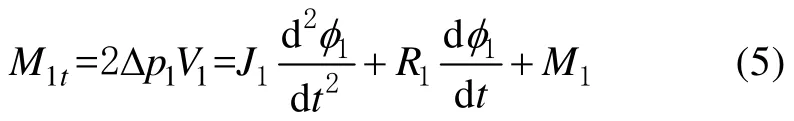
式中：M1t为二次元件理论输出转矩，N·m；M1为二次元件实际输出转矩，N·m；Δp1为二次元件油口压差，MPa；V1为二次元件排量，m3/rad；J1为二次元件输出端及联轴器输入轴等效转动惯量，kg·m2；R1为二次元件等效阻尼系数，N·m·s/rad；φ1为二次元件转角，rad。

由于左、右轮边和二次输出均为输出加载单元，结构形式及模型完全相同，以二次输出加载单元为例，建立加载单元二次元件的力矩平衡方程：

式中：Δp2为二次元件油口压差，MPa；V2为二次元件排量，m3/rad；J2为二次元件输出端及弹联轴器输出轴等效转动惯量，kg·m2；R2为二次元件阻尼系数，N·m·s/rad；φ2为二次元件转角，rad。

加载轮桥等效物理模型如图2所示。根据图2，忽略柔性环节及传动时的差速问题可建立加载轮桥等效力矩平衡方程：

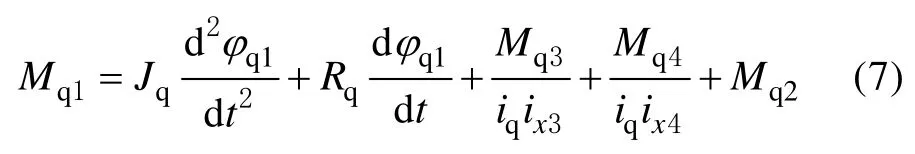
式中：Mq1为轮桥输入轴转矩，N·m；Mq2为轮桥二次输出轴转矩，N·m；Mq3为左轮边输出轴转矩，N·m；Mq4为右轮边输出轴转矩，N·m；Jq为整个轮桥等效转动惯量，kg·m2；Rq为整个轮桥等效阻尼系数，N·m·s/rad；iq为传动桥速比；ix3为左轮边减速器传动比；ix4为右轮边减速器传动比；φq1为输入轴转角，rad。

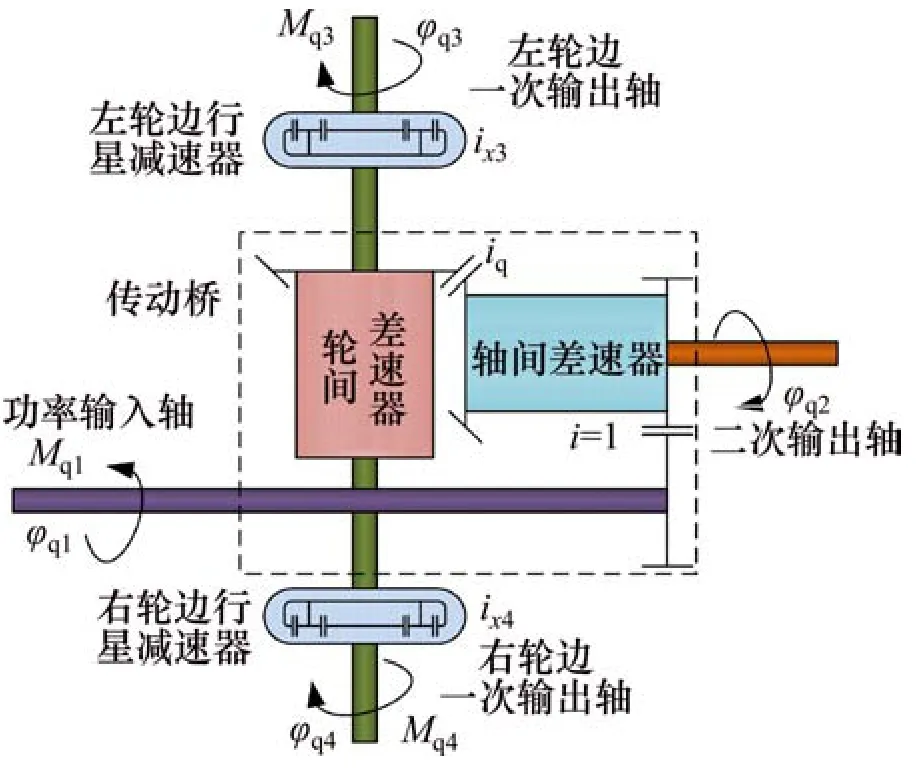
图2 轮桥物理模型Fig.2 Physical model of wheel-bridge

对式(1)～(7)进行拉氏变换，按照试验台机械件的参数整理系统比例环节和阻尼环节。各环节具体表示如下。

转速、转矩系统二次元件及传感器综合传递函数为

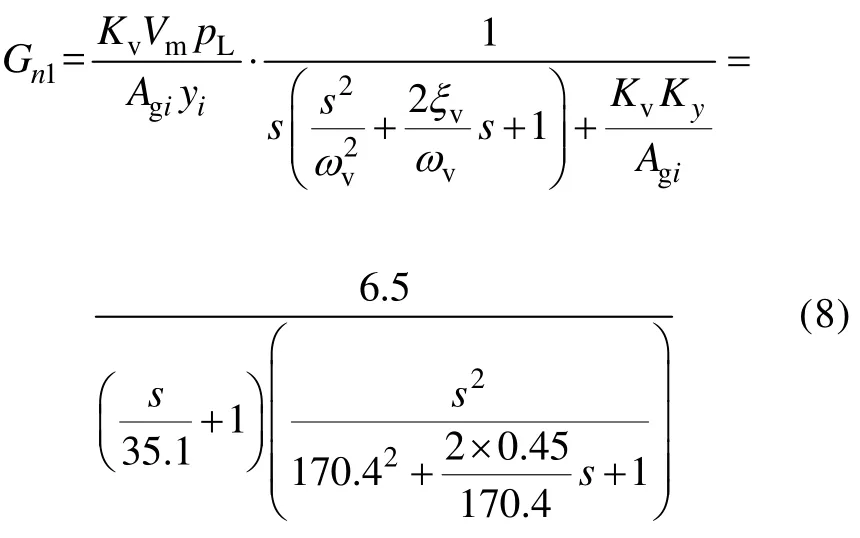
式中：n=1，2，3，4；pL为网络负载压力；Ky为位移传感器变换系数。

加载系统机械件综合惯性阻尼环节传递函数为

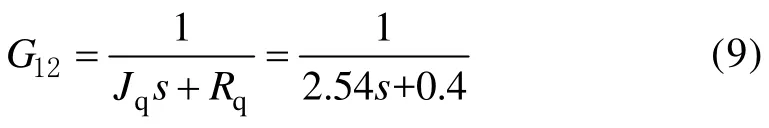
加载系统机械输入端比例环节传递函数为

式中：ib1为驱动变速器传动比；ib2为二次输变速器传动比；ib3和ib4分别为左、右轮边变速器传动比。

转速传感器变换系数：K11=0.019 2；转矩传感器变换系数：K21=0.004 95；K31=K41=0.009 91；系统输出端比例环节传递函数：K22=K32=K42=0.232。

根据上述推导，在系统前置级排量阀控缸模型中加入微分滤波PID控制器[20]，可得整个系统的传递函数方块图模型如图3所示。图3中，N1i～N1o为驱动单元转速控制系统，M2i～M2o为传动桥二次输出单元的转矩控制系统，M3i～M3o和M4i～M4o分别为左、右轮边输出单元的转矩控制系统。在整个系统中，转速系统受转矩系统的直接控制；转速系统又通过惯性阻尼环节控制转矩系统，因此，系统驱动转速与输出转矩存在一定程度的耦合干扰问题。

3 对角解耦控制矩阵的求解

为了解决试验台加载系统转速与转矩间的耦合干扰问题，对试验台取用对角矩阵解耦[21]控制方法。根据试验台的输入、输出模型可知，实现系统解耦需使系统的传递函数为对角矩阵形式。因此，为实现传递函数对角化，在模拟加载系统各单元之间引入特定的非奇异解耦矩阵E12，E13，E14，E21，E31和E41，如图4所示。根据图4解耦控制模型，中间变量X1，X2，X3和X4与控制变量e1，e2，e3和e4以及系统输出变量N1o，M2o，M3o和M4o之间关系可表示如下：

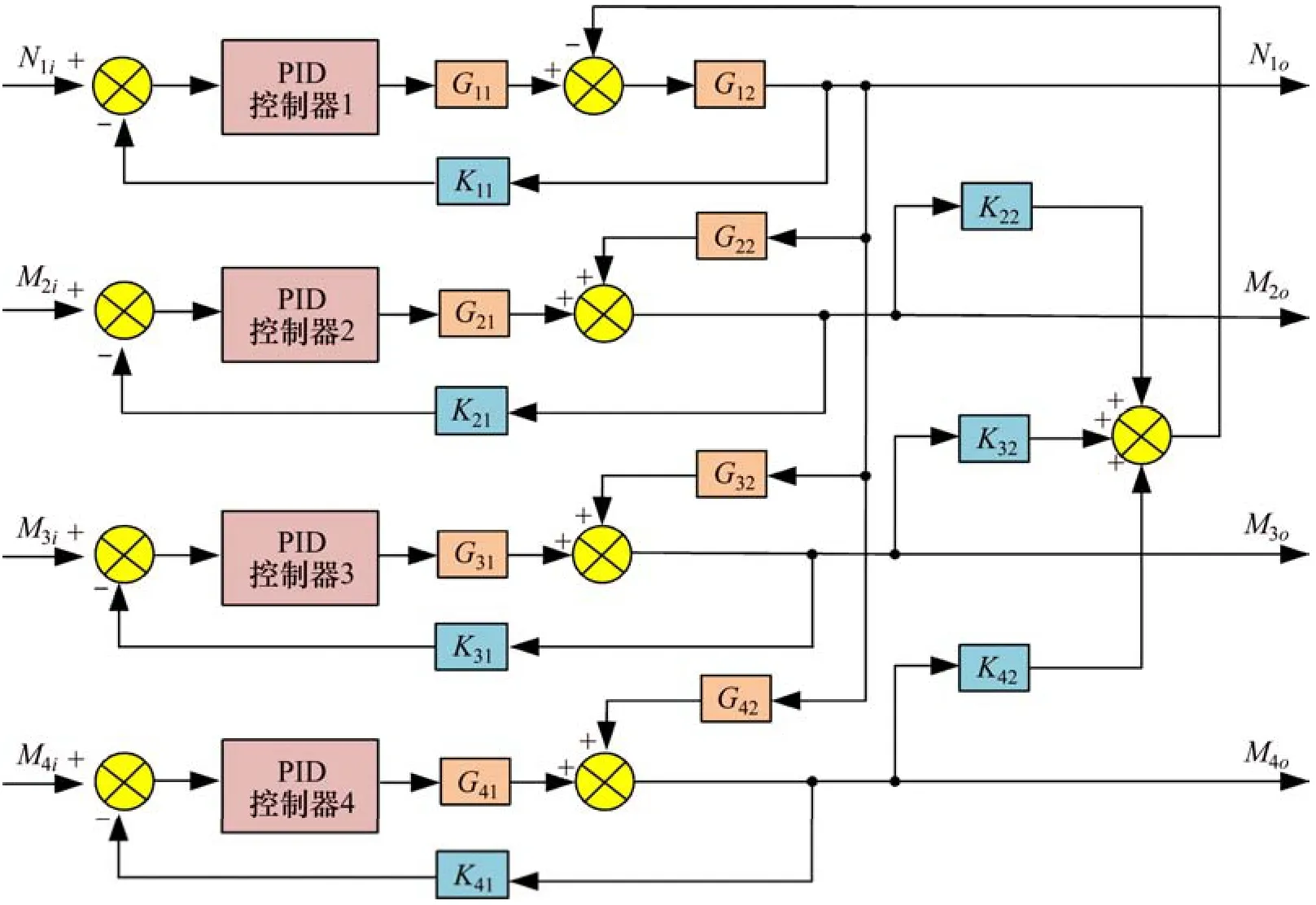
图3 PID控制的模拟加载系统方块图Fig.3 Block diagram of PID controlled analog loading system

由式(11)和式(12)得：

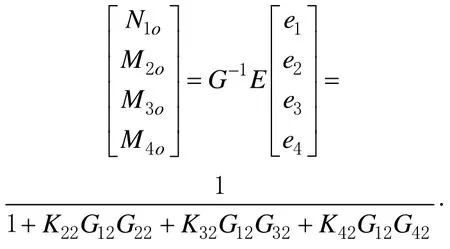
将矩阵A对角化并根据各环节具体参数求得解耦矩阵为

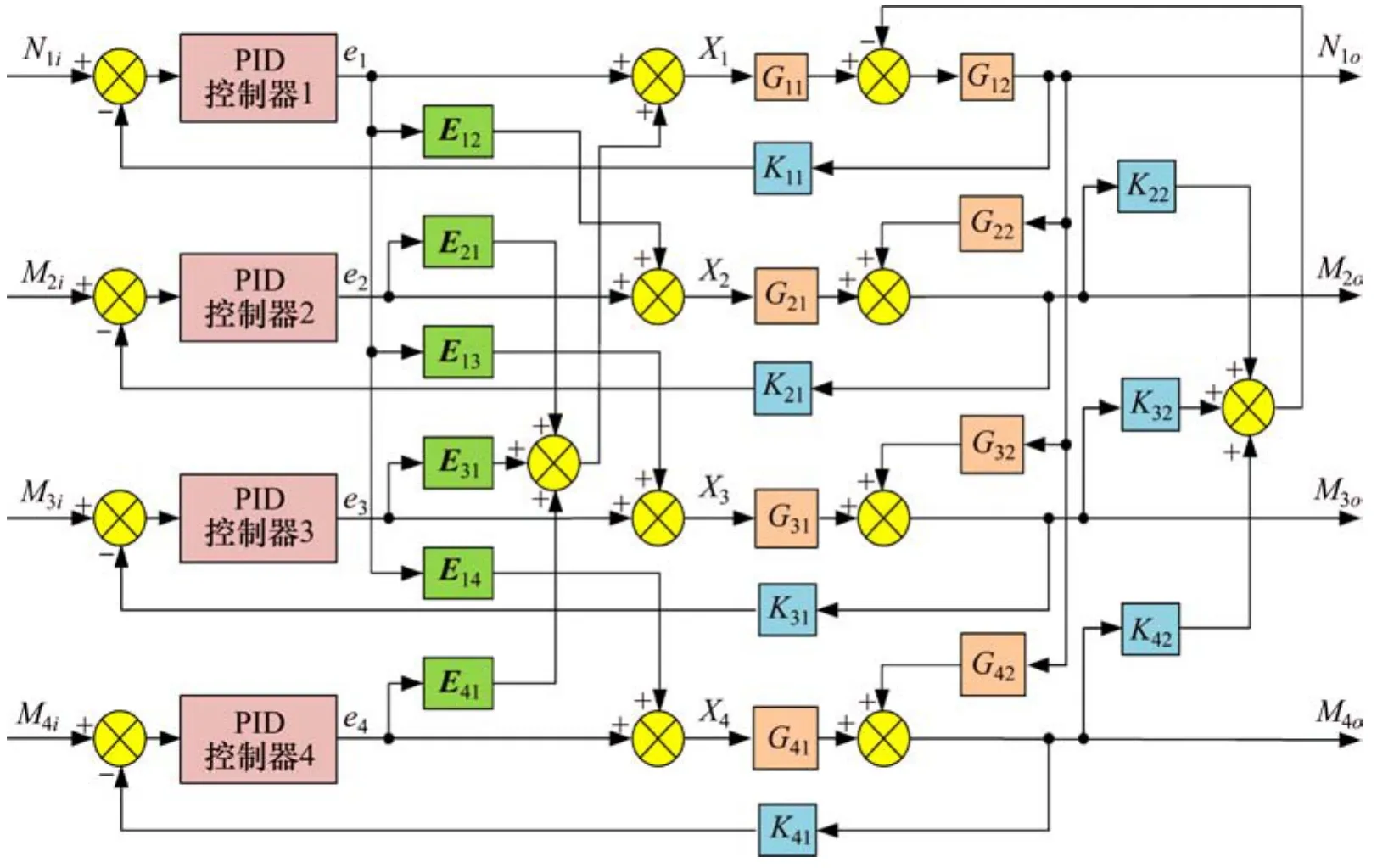
图4 解耦控制的模拟加载系统方块图Fig.4 Block diagram of an analog loading system controlled by decoupling

将解耦矩阵与工控机逻辑控制程序构成解耦控制系统，通过上位机完成加载系统的解耦控制。

4 实验研究

为研究试验台驱动转速和输出转矩间的耦合干扰问题，验证解耦控制手段的有效性，参照图1搭建模拟加载试验台如图5所示。

图5 试验台实物和实验现场Fig.5 Physical and experimental site of test rig

试验加载系统各单元前置级排量控制所用电液伺服阀和变量液压缸主要参数如表1所示。

试验加载系统各单元所用二次元件参数相同，型号为力士乐A4VSO250 DS型，主要参数见表2。

试验台加载系统各机械单元所用仪器规格一致，部分参数如表3所示。

表1 前置级排量控制参数Table 1 Pre-stage displacement control parameters

表2 二次元件参数Table 2 Secondary element parameters

表3 加载机械系统参数Table 3 Loading mechanical system parameters

将表2和3中各参数输入到上位机各环节的传递函数中，即可利用试验台进行相关实验。

4.1 耦合干扰实验

4.1.1 驱动转速波动干扰实验

在试验台计算机控制系统中，依次设置试验台各加载参数，在未引入解耦控制情况下，进行驱动转速正弦波动干扰实验。其中，驱动转速正弦波动频率依次设置为0.5，1.0和2.0 Hz，转速幅值设置为60 r/min。实验结果曲线如图6所示。图6(a)，(b)和(c)所示分别为3种频率下驱动转速波动对二次输出转矩、轮边（左右相同）输出转矩的干扰实验曲线；图6(d)，(e)和(f)所示分别为3种频率下二次输出转矩的误差曲线；图6(g)，(h)和(i)所示分别为 3种频率下轮边输出转矩的误差曲线。

由图6可知：驱动转速的波动导致二次输出转矩和轮边输出转矩不同程度的波动，且驱动转速波动频率上升，二次输出转矩和轮边输出转矩的波动误差增加；当驱动转速波动频率为0.5 Hz 时，二次输出转矩的最大波动误差为15 N·m，轮边输出转矩的最大波动误差为7 N·m；2.0 Hz时，二次输出转矩的最大波动误差为 30 N·m，轮边输出转矩的最大波动误差为13 N·m。

4.1.2 输出转矩波动干扰实验

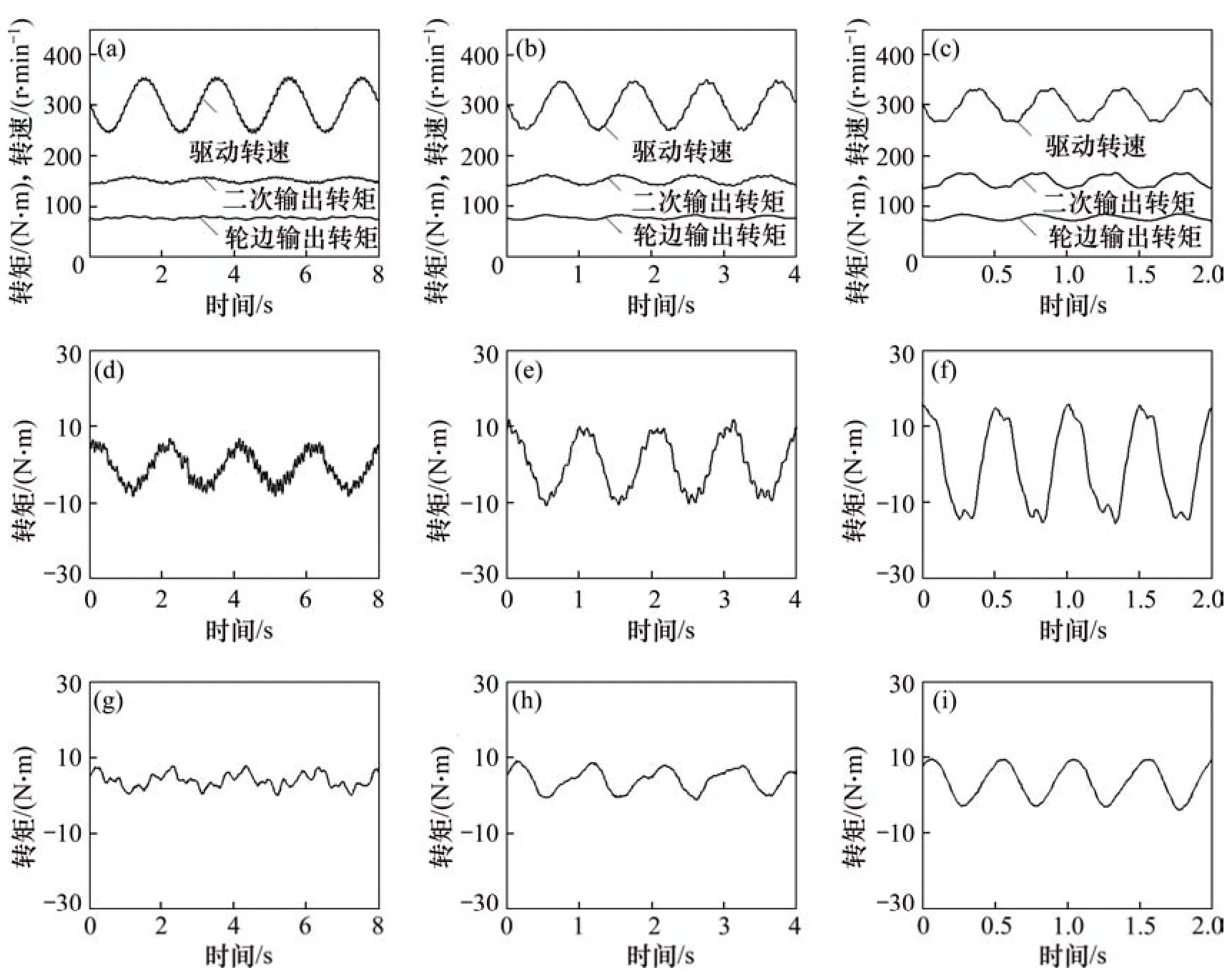
图6 驱动转速波动干扰实验曲线Fig.6 Experimental curves of driving speed fluctuation interference

二次输出转矩与轮边输出转矩均为系统输出端，且对转速的干扰情况相同，因此，以二次输出转矩为例，讨论转矩波动干扰对驱动转速影响。

实验参数与驱动转速波动干扰实验相同，二次输出转矩正弦波动频率依次设置为0.5，1.0和2.0 Hz；幅值设置为 80 N·m。实验结果曲线如图7所示。图7(a)，(b)和(c)所示分别为3种频率下二次输出转矩波动对驱动转速的干扰实验曲线；图7(d)，(e)和(f)所示分别为3种频率下驱动转速的误差曲线。

由图7可知：二次输出转矩以一定的频率进行波动时，驱动转速将产生较大波动误差。与驱动转速波动干扰情况不同之处在于，二次输出转矩波动时，驱动转速的波动误差随波动频率的增加而减小。当二次输出转矩波动频率为0.5 Hz时，驱动转速的最大波动误差为18 r/min；二次输出转矩波动频率为2.0 Hz时驱动转速的最大波动误差为15 r/min。

4.2 解耦控制实验

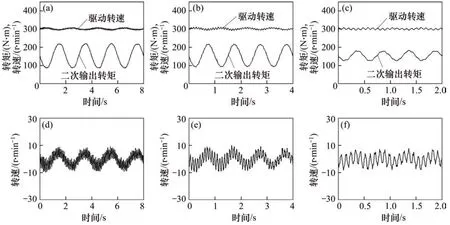
图7 二次输出转矩波动干扰实验曲线Fig.7 Experimental curves of disturbance of secondary output torque ripple

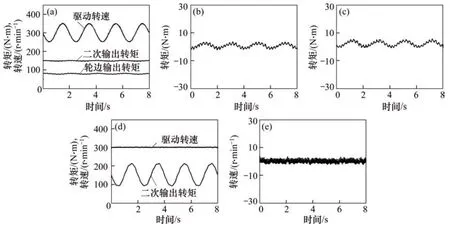
图8 解耦控制实验曲线Fig.8 Experimental curves of decoupling control

为便于同未解耦时的干扰试验结果进行比较，解耦实验的条件及参数与耦合干扰实验保持一致，取波动干扰为0.5Hz的情况进行讨论，引入解耦控制后的实验结果如图8所示。图8(a)所示为驱动转速波动干扰下的解耦控制实验曲线；图8(b)和(c)所示分别为解耦后二次输出加载转矩和轮边加载转矩的误差曲线；图8(d)所示为二次输出转矩波动干扰下的解耦控制实验曲线；图8(e)所示为解耦后驱动转速的误差曲线。

由图8可知：引入解耦控制后，二次输出转矩和轮边输出转矩的最大波动误差均控制在5 N·m，驱动转速最大波动误差控制在4 r/min。与未进行解耦控制的实验结果进行对比可知：二次输出加载转矩最大波动误差减小 67%，轮边加载转矩最大波动误差减小29%；驱动转速最大波动误差减小78%。

5 结论

1)通过耦合干扰实验，轮桥模拟加载试验台驱动转速和输出转矩之间存在一定程度的耦合干扰，其主要表现为：驱动转速的波动引起二次输出转矩和轮边输出转矩不同程度的波动，当驱动转速的波动频率增加时，二次输出转矩和轮边输出转矩的波动误差增加；输出转矩的波动引起驱动转速产生较大的波动误差；当输出转矩波动频率增加时，驱动转速的波动误差减小。

2)通过对试验台驱动转速和输出转矩进行解耦控制，驱动转速因输出转矩波动引起的最大波动误差比解耦前减小78%；二次输出转矩和轮边输出转矩因驱动转速波动而引起的最大波动误差比解耦前减小近67%和29%。利用对角矩阵对试验台进行解耦控制，大幅度减小了耦合干扰的影响，解耦效果有效，从而提高了试验台的控制性能和稳定性。