改进的Sage⁃Husa自适应滤波算法在MEMS航姿参考系统中的应用

路小燕，杨柳庆，郭 锦，杨 硕，王博豪

（1.南京航空航天大学自动化学院，南京210016；2.南京航空航天大学无人机研究院，南京210016）

0 引言

航姿参考系统（AHRS）是一种在空间三维坐标系中用于精确测量载体姿态（俯仰角、滚转角、航向角）的惯性装置系统，包括了MEMS中的陀螺仪、磁力计和加速度计。三轴陀螺仪的测量结果在短时间内精度较高，但误差会随时间的推移而累积；磁力计和加速度计为姿态运动载体提供了更加精确的静态角度，但是动态性能差［1］。常规的Kalman滤波器的增益和预测调整能力存在缺陷，在计算时只依据先验信息，没有引入实际观测值。随着数据的增加，Kalman滤波会出现饱和现象，导致滤波器失去原有用途。无人飞行系统大部分都是非线性的系统，扩展Kalman滤波利用Taylor级数展开法将无人非线性系统线性化，然后采用Kalman滤波的相关步骤更新系统状态［2-3］。 文献［4］设计了基于四元素的九态扩展Kalman滤波算法。此算法适合弱的非线性系统，实时性差且滤波容易发散。文献［5］和文献［6］提出了一种利用Sage-Husa自适应滤波对系统和量测噪声进行实时估计的算法，此算法在各领域中得到了广泛运用，但该算法在与工程应用结合时会出现许多问题。文献［7］和文献［8］提出了 Sage-Husa自适应滤波的简化改进算法，在滤波过程中直接忽略了单个采样周期内的在线估计，在滤波的某个时间段内因观测值误差增大而致使新息中被引入误差量，从而导致状态预测出现了发散，无法适应情况突变时的导航精度的需求，鲁棒性差。

自适应滤波在利用观测信息进行滤波时，不断对不确切或者未知的模型参数、噪声统计特性进行实时估计与修正，减小了相关模型的误差与算法的计算量［9-11］。自适应滤波包含许多种类，如新息自适应估计Kalman滤波算法、协方差匹配法、相关法、Bayes估计法、极大似然法、模糊自适应滤波法、Sage-Husa自适应滤波算法等［12-15］。Sage-Husa自适应滤波算法通过极大后验（MAP）信息对量测噪声和系统噪声进行估计，具有易造成滤波发散、计算量大与实时性较差的缺点。本文针对Sage-Husa自适应滤波算法进行了改进，将新的算法应用于基于多传感器融合的航姿参考系统中，实时估计并解算无人机的姿态。

1 定姿方案

1.1 整体定姿方案

如图1所示，本文利用三轴陀螺仪估计的姿态角作为过程信息，将磁力计与加速度计估算的角度作为量测信息，将各个传感器的优劣势进行互补，建立了改进的Sage-Husa自适应Kalman滤波算法，对融合多传感器信息的航姿参考系统进行无人机姿态的最优估计。

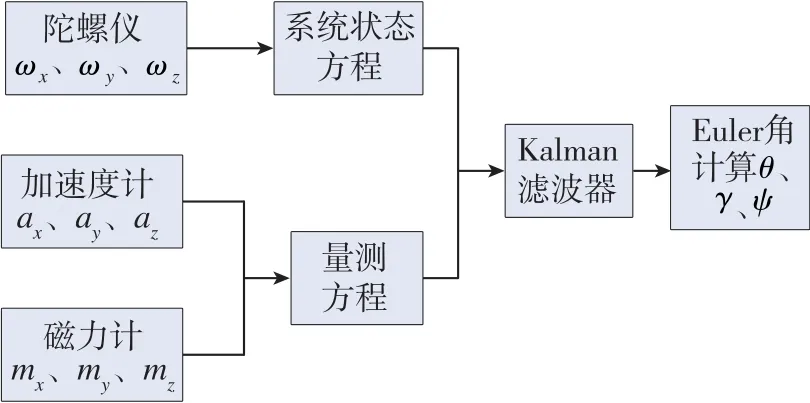
图1 定姿总体结构图Fig.1 Overall structure diagram of attitude determination

1.2 三轴陀螺仪定姿算法

陀螺仪本身存在姿态累计误差问题，其直接获取的数据也掺夹着外界的噪声。因此，在对传感器原始数据进行零漂补偿和误差补偿后，假设运动载体处在非加速度状态，在k时刻姿态角的真实值为三轴陀螺仪的角度估计误差值为由于采用Euler角法计算的姿态角会产生奇异值，进而可采用四元素法求取三轴陀螺仪的航姿角度故有

基于工程需求，为了消除Euler角解算无人飞行系统姿态而产生的奇点，由四元素法得到的矩阵坐标变换矩阵如下式所示

此时，得到四元素微分向量方程为

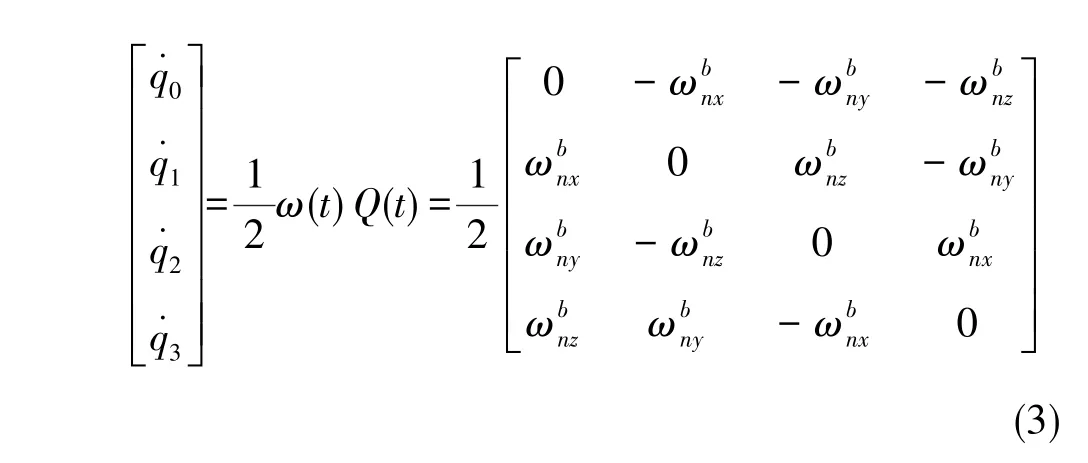
采用四阶Runge-Kutta法求解四元素微分方程，令T为更新步长，计算得到量测更新K阵与Q阵的更新表达式为

四阶Runge-Kutta法吸取了Taylor展开法中精度高的理念，同时摒弃了高阶求导的难点，令数值结果紧凑而对称。四阶Runge-Kutta法是解算微分方程的有利工具，具有很好的工程意义。将式（5）代入Euler角解算式，可得出无人机姿态角

状态向量x（k）＝［θγψbxbybz］取自Euler角与陀螺的漂移。利用Euler角的微分方程式及MEMS陀螺仪的误差模型表达式，可以得到如下的系统状态方程

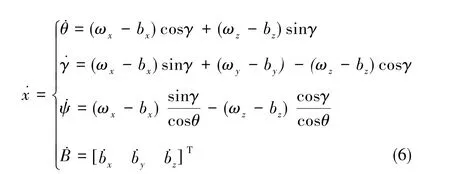
1.3 磁力计和加速度计姿态更新算法

当运动载体处于静止或匀速运动状态时，磁力计和加速度计所采集到的信息滤波经处理后可得到姿态角信息为磁力计与加速度计的估计误差间的差值，故有

运动载体为任意姿态时，假设测量运动加速度在三轴坐标系上的表达式为

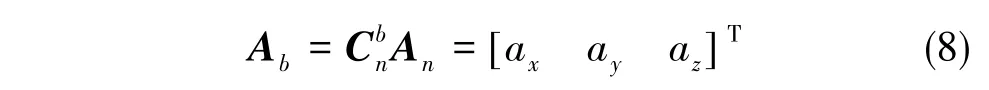
令g0为当地重力加速度，则有

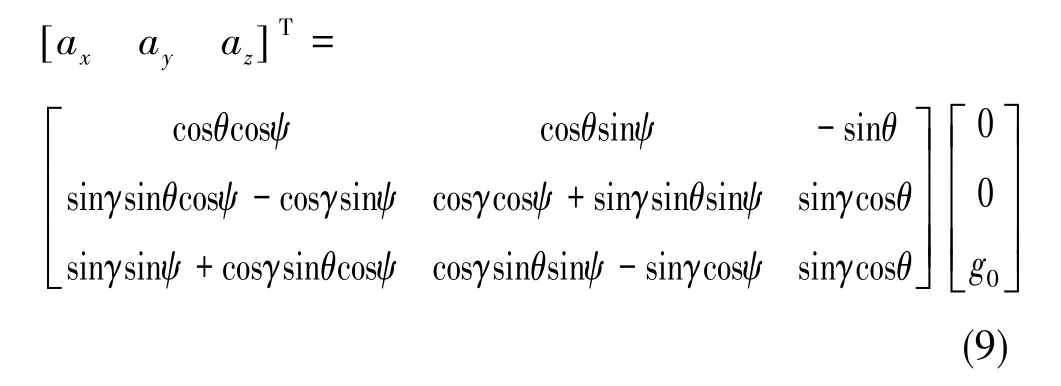
其中，Cbn为捷联式惯导的方向余弦矩阵，从而可解算出俯仰角与橫滚角

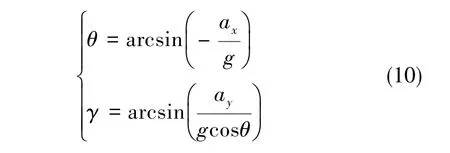
磁力计可应用于水平方位航向角的计算。其中，mx和my分别为地磁场在机体轴X轴、Y轴上的分量，Δψ为磁偏角，ψm为机体纵轴相对磁场指北方位的航向角。假设ψ为机体轴纵轴相对真实指北方位的航向角，则有

可建立系统观测方程y＝h（xk）+v。 其中，v＝［v1v2v3v4］为系统的量测噪声，h（xk）＝［-cosθsinγsinθsinψcosθcosψcosθ］T。

运动载体的姿态是不断变化的，故量测系统存在俯仰角与滚转角姿态的修正

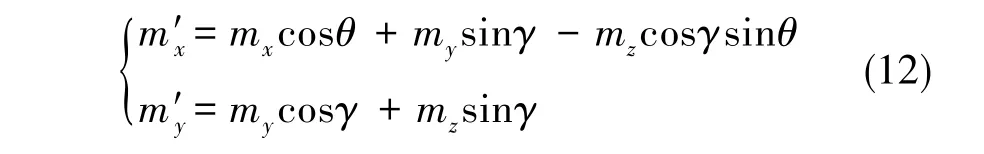
2 改进Sage-Husa自适应滤波算法

2.1 简化Sage-Husa自适应扩展Kalman滤波

扩展Kalman滤波算法在其被使用之前就假定系统的噪声统计特性为已知，而在实际的应用中，无人飞行系统的系统噪声的方差值和由观测得到的噪声误差会随时间而变动，扩展Kalman滤波算法会使姿态解算值产生发散。Sage-Husa自适应扩展滤波算法的核心是实时运用量测更新的数据对系统和量测噪声的特性进行动态的统计估算，并最终解算出所求的状态参数的预测值，减少由模型误差参数带来的影响［16］。

Sage-Husa自适应扩展滤波算法无法在系统和量测噪声都未知的条件下进行估算，本文将在系统噪声矩阵已知的情况下估测量测噪声方差矩阵。基于三轴陀螺仪计算所得的状态方程与磁力计、加速度计描述的量测方程，得到多传感器融合的简化Sage-Husa自适应扩展滤波算法［17］。该算法本身已消除了传感源自有的错误，其算法更新的基本步骤如式（13）与式（14）所示。

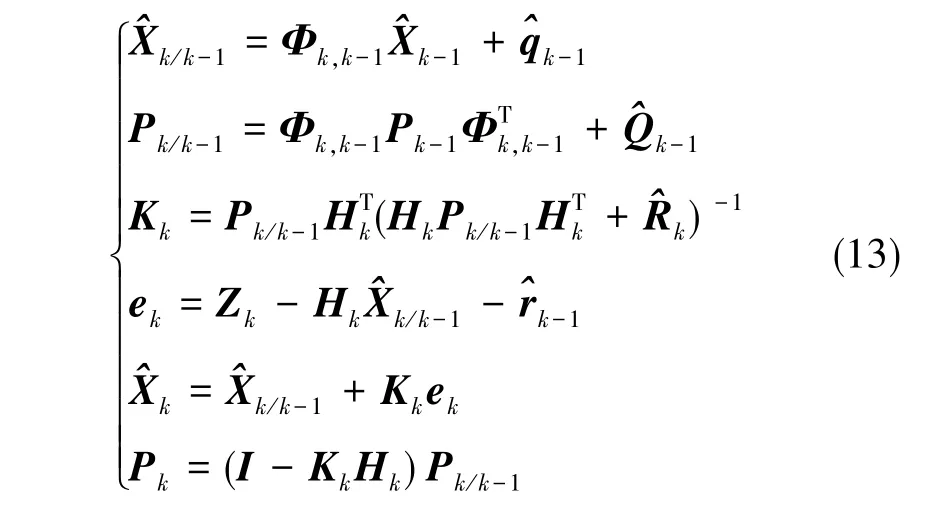
具有时变性能的噪声估计器如下

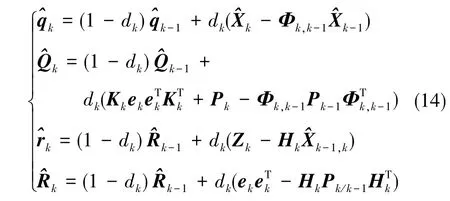
定义式（14）中dk＝（1-b）/（1-bk+1）中b的取值范围为0＜b＜1， 并将其作为遗忘因子，遗忘因子的取值区间一般为［0.95， 0.99］。 将解算得到的当前时刻的状态值、误差方差、增益值等作为下一时刻的初始值，不断进行迭代，则可得到Sage-Husa 自适应滤波算法［18］。

2.2 Sage-Husa自适应滤波算法的改进

理论而言，Sage-Husa自适应滤波算法可以同时在线估计出系统的噪声＾Qk及量测噪声＾Rk。但是，ek的异常改变会影响＾Qk和＾Rk的计算准确性，从而得到不精确的滤波效果。在实际工程应用中，Sage-Husa自适应扩展Kalman滤波实现性强、精确度高，但其计算量较大，并且鲁棒性较差。因此，对Sage-Husa自适应滤波算法进行改进，显得尤为重要［19］。

（1）最佳遗忘因子的选择

在Sage-Husa自适应滤波算法中，遗忘因子b选择的恰当与否直接关系到滤波的精度及滤波是否会出现发散现象。很多学者利用试凑法和最优估计算法，将每次迭代得到的遗忘因子解算出来，从而得到最优的滤波算法。为了对滤波状况进行判断，本文采用了预测残差作为监测的方法。若滤波出现发散，则有

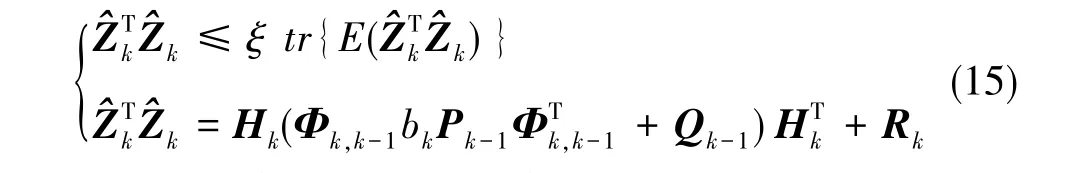
当储备系数ξ的取值为1时，可得到最佳的滤波估计效果。将式（15）代入式（14），可求取遗忘因子的最优值

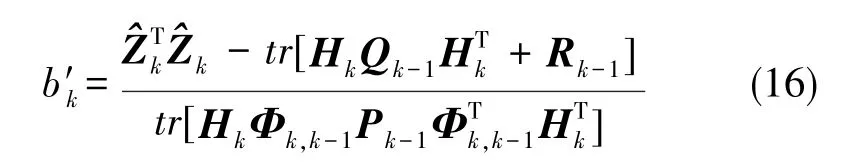
综上所述， 式（14）与式（16）的组合构成了由最佳遗忘因子改进的Sage-Husa自适应滤波算法，提高了滤波的鲁棒性。

（2）抑制Sage-Husa自适应滤波的发散

Sage-Husa自适应滤波是一种具有次优性质的滤波，次优滤波算法在运用一步预测值和滤波值来替代全平滑值时将可能得到精度较差的噪声统计特性。为了使得Qk与Rk满足无偏估计，可在式（14）中采用两式相减的算法，这将会致使Qk和Rk失去正定性与对称性。以上两种不足将会引发滤波结果发散，因而本文将采用下面两种方法抑制滤波发散。

①使用有偏估计，进而保证Qk和Rk的对称性与正定性

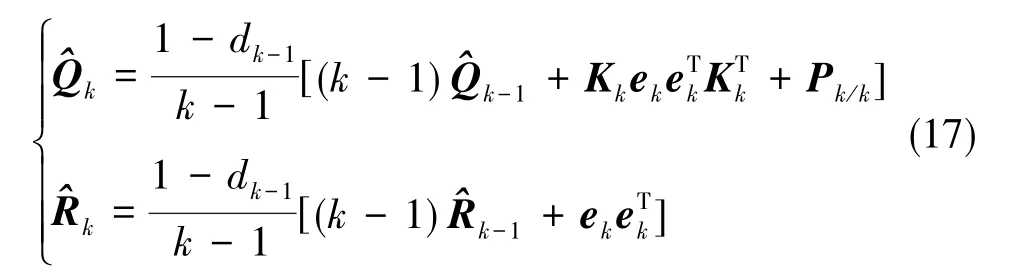
对＾Qk和＾Rk进行实时监控，如果＾Rk为正定矩阵，＾Qk为半正定或正定矩阵，则利用式（14）进行求解，否则利用式（17）进行求解。

②通过调整和修正Pk/k-1，进而调控增益矩阵Kk， 来防止出现滤波发散现象

其中，ρ≥1为可变系数，它的取值越小，滤波发散的抑制性能越强。如果式（18）不成立，则用代替式表达如下

其中，Sk为滤波加权系数，其取值为1。

3 实验验证

3.1 Matlab仿真验证

选取遗忘因子数值为0.95，滤波初始值为X0＝［0 0 0 0 0 0］T， 协方差初始值为 P0＝0.00052·I6×6， 量测噪声方差矩阵初值为 R0＝［0.0005 0.0005 0.0005］， 系统噪声矩阵Q0＝0.0182·I6×6。 在 Matlab 中， 采样时间为 0.1s， 仿真总时间为600s，可得出多传感器融合算法下的Kalman滤波、自适应Sage-Husa扩展Kalman滤波与改进的自适应Sage-Husa扩展Kalman滤波这3种不同算法下的航姿误差对比图，如图2～图4及表1所示。

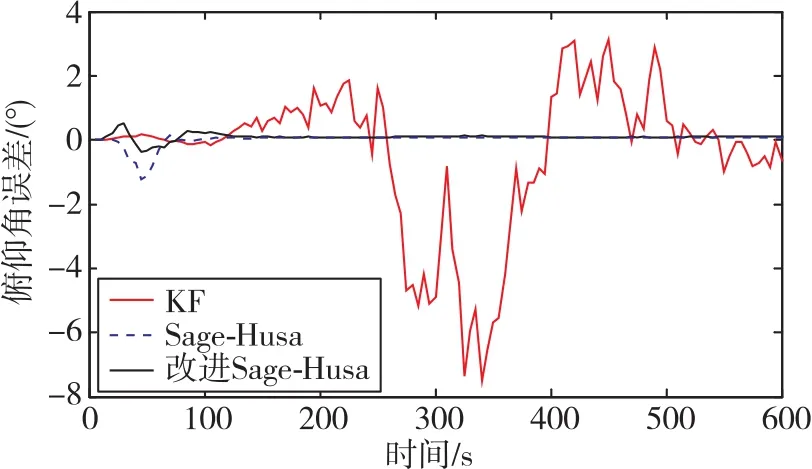
图2 俯仰角误差曲线Fig.2 Curves of pitch angle error

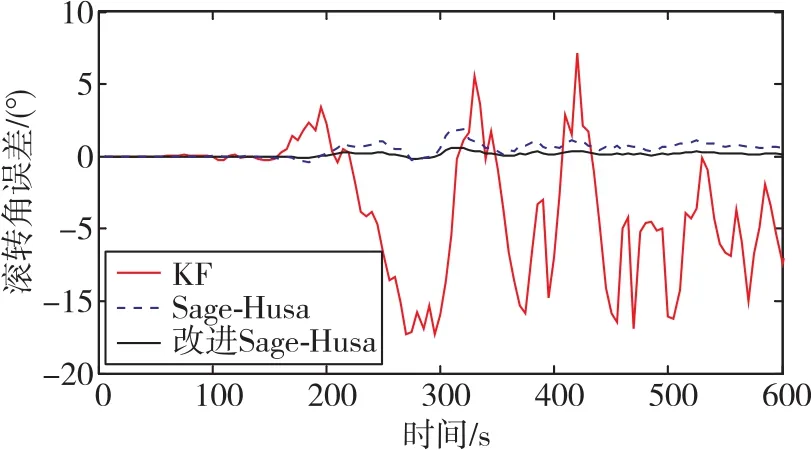
图3 滚转角误差曲线Fig.3 Curves of roll angle error

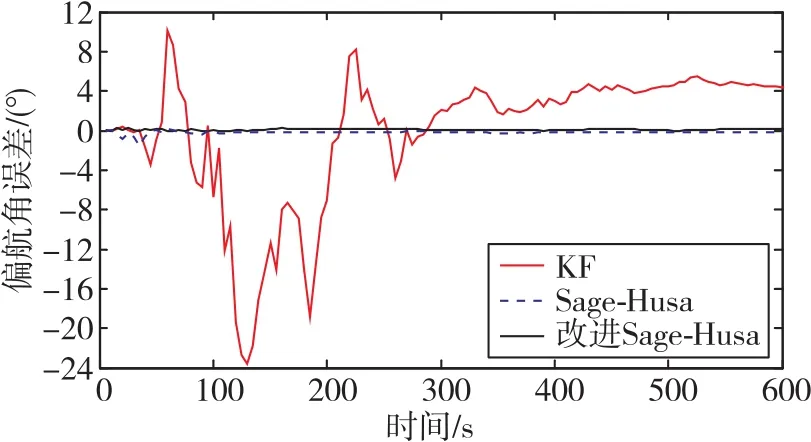
图4 航向角误差曲线Fig.4 Curves of yaw angle error

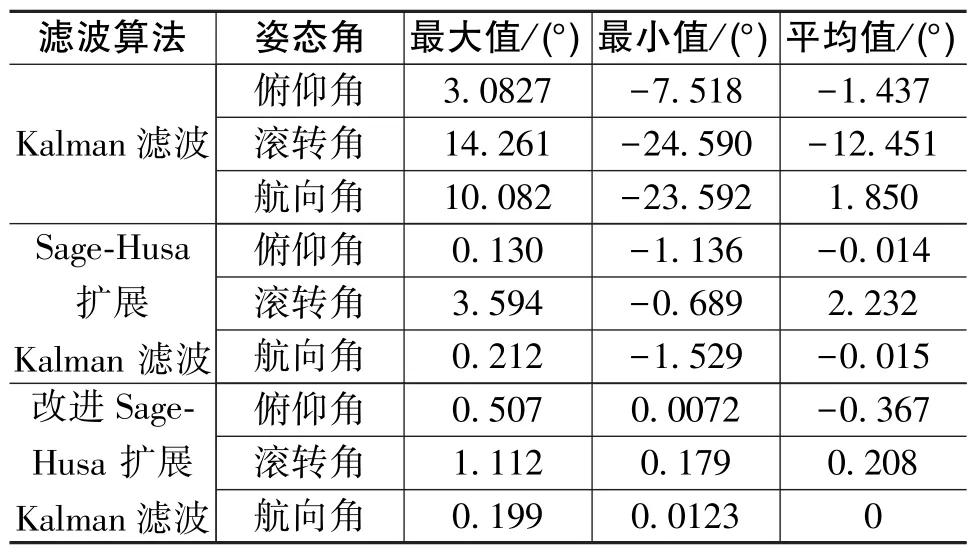
表1 各滤波算法下的姿态误差Table 1 Attitude errors under various filter algorithms

从图2～图4及表1中可以看出，基于多传感器融合下的经典Kalman滤波算法的姿态误差大，有明显的波动，并且俯仰角误差和滚转角误差的波动随时间推移而呈现出了发散趋势，即使在当航向角误差在300s后稳定下来时，误差依旧超过了4°，无法满足高精度导航的需求；相比经典Kalman滤波算法，自适应Sage-Husa扩展Kalman滤波算法的融合精度有明显的提高，从理论上而言其可被用于对导航精度需求较低的无人飞行系统，但是其误差值的绝对值在一定时间范围内依然偏大，也无法满足高精度导航的需求；改进自适应Sage-Husa算法不仅可抑制滤波发散，而且可令航姿误差绝对值明显降低，提高了航姿系统的鲁棒性。Matlab仿真实验为后续的实验室实物搭建时的姿态算法估计试验奠定了基础。

3.2 基于航向角的航姿系统算法验证

本实验搭建了ARM9+惯导+OEM板的航姿系统，惯导模块为GY953的低成本航姿模块（包含加速度计、陀螺仪及磁场感应器，通过I2C接口与总线连接进行导航数据的收发），原始数据为航姿参考系统被置于三轴转台上时GY953模块内置的经典四元数算法直接解算的导航姿态角数值。

在实验室条件下转动三轴转台，不间断地改变航姿系统的航向。本次实验选用基于扩展Kalman滤波的自适应Sage-Husa滤波和基于扩展Kalman滤波的改进自适应Sage-Husa滤波2种算法对无人航姿系统进行姿态解算。与GY953模块的原始解算数据进行比较，通过数据传输模块及人机交互界面将实验室模拟飞行数据传输并保存在EXL表格中，然后将实际模拟飞行的EXL表格数据导入到Matlab中，进行姿态仿真验证。本实验对无人飞行系统的姿态角（俯仰角、滚转角及航向角）进行算法数据仿真，并以航向角为例对其姿态误差进行了对比分析，具体分析结果如图5～图8所示。

图5 俯仰角曲线Fig.5 Curves of pitch angle

图6 滚转角曲线Fig.6 Curves of roll angle

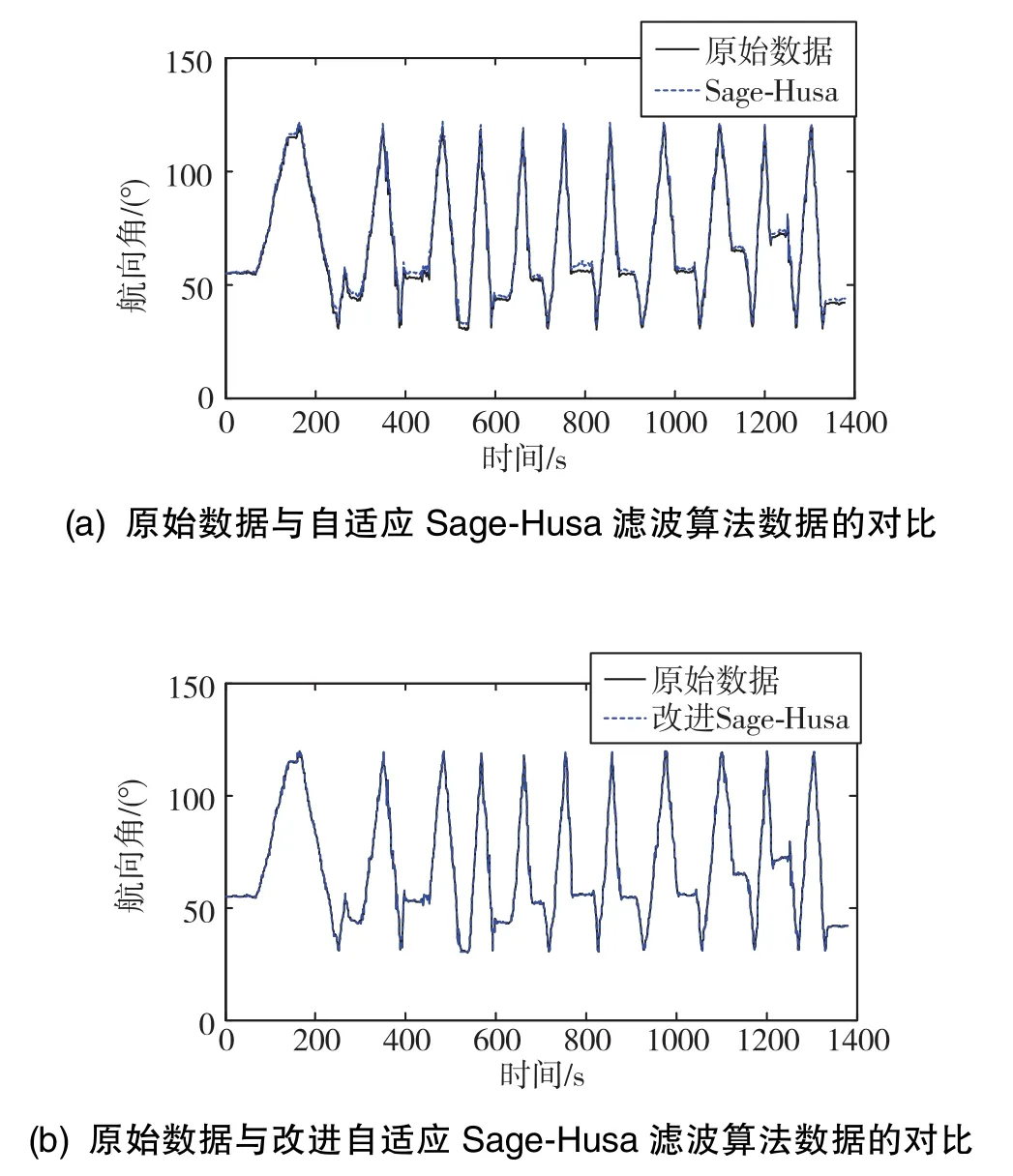
图7 航向角曲线Fig.7 Curves of yaw angle

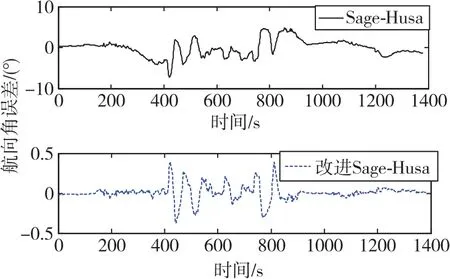
图8 两种方法的航向角误差曲线Fig.8 Yaw angle error curves of the two methods

由图5～图8可以看出，自适应Sage-Husa扩展Kalman滤波算法误差在-8°～7°之间。由于动态性的影响，其算法误差比单纯的Matlab软件仿真实验要大；而改进的自适应Sage-Husa算法的俯仰角误差绝对值保持在0.2°以内，滚转角误差绝对值均小于0.18°，航向角误差最大绝对值也小于0.4°。其相比自适应Sage-Husa算法的精度提高了一个数量级，可有效地对微小型无人机航姿进行跟踪。

4 结论

本文应用的多传感器信息融合（将陀螺仪输出数据作为预测信息，将磁力计与加速度计输出数据作为观测信息）算法满足了微小型无人机对低复杂度和高精度的需求。仿真实验和模拟飞行试验有效证明了基于EKF改进的自适应Sage-Husa算法在抑制滤波发散的同时提高了算法的稳定性与实时性。此算法精度高、实时性强、计算量少且具有良好的工程应用价值，可应用于低成本、高精度的航姿参考平台系统中。