极端瞬态力作用下金属壳谐振陀螺结构强度分析
2019-06-12张小宇
刘 宁, 苏 中, 张小宇
(1.北京信息科技大学高动态导航技术北京市重点实验室,北京100101;2.北京信息科技大学现代测控技术教育部重点实验室,北京100101)
0 引言
综合国内外研究现状,对于极端瞬态力作用下金属壳谐振陀螺结构强度的分析,大多采用有限元数值分析方法。其中,具有代表性的是美国的Chakka等人。他们利用显式动力学有限元分析方法分析了美军M795型号弹药在发射过程中整个弹体结构、惯性组件及制导组件的抗过载性能,并进行了实际验证[1-3]。国内的南京理工大学、中北大学、北京遥测技术研究所等机构的相关研究人员利用有限元仿真方法分析了MEMS陀螺的结构设计、二次灌封和封装保护等问题[4-6],并通过试验对相关结果进行了有效验证。研究人员所采用的分析方法可分为动态法和静态法两种,其中前者分析的是冲击过程中的受力情况,后者是通过施加特定冲击力或冲击谱进行受力分析,两者均可验证惯性器件的抗过载性能[7-10]。
在进行钟形振子式角速率陀螺抗高过载性能分析时,采用了动态法进行分析。通过建立有限元模型,施加约束载荷,分析了钟形振子不同结构参数的整体受力情况,确保钟形振子在冲击过程中不会发生塑性形变,从而满足抗高过载要求。
1 陀螺工作原理
在钟形振子的钟壁上,均匀布置了4对压电电极,如图1所示。压电电极分别为1对激励电极、1对检测电极、1对反馈电极和1对阻尼控制电极。利用压电材料的逆压电效应,来激励钟形振子振动,使钟形振子底部的惯性质量部分——钟唇在环向上产生四波腹振动的驻波形式,并定义这种振动模态为激励模态,或称主模态。对于这种轴对称壳而言,其在同一振动频率下会有两种固有振型,这两种振型相差45°,定义与主模态相差45°的模态为检测模态,或称第二模态。而这两种振动模态形成的相差45°的振型,可通过哥氏力进行耦合。

图1 钟形振子压电电极分布图Fig.1 Piezoelectric electrode distribution diagram of bell-shaped oscillator
在具体实施过程中,压电电极应摆放在远离自由端、靠近约束端的位置,以尽可能减少由于自由端受哥氏力作用而产生的对压电电极检测效果的影响。首先,在激励电极上施加交流信号,压电电极将沿长度方向发生变化,产生驱动力。相应质点在该驱动力的作用下,沿垂直于钟壁的方向运动,最终激励钟形振子工作于四波腹振型。
当敏感轴方向上无角速率输入时,钟形振子在激励电极的驱动下,维持在激励模态下振动;当敏感轴方向上存在输入角速率时,在哥氏力的耦合作用下激励出检测模态,且该模态下振型的振动幅值应正比于输入角速率。而当两个模态均作用于钟形振子上,就会引发原有的四波腹振型发生偏转,或描述为驻波发生进动。在实际工作时,当敏感轴方向上存在逆时针方向的角速率Ω时,驻波将产生进动,其振型进动角为ϑ,正比于输入角速率Ω,如图2所示。

图2 钟形振子驻波进动示意图Fig.2 Schematic diagram of standing wave precession of bell-shaped oscillator
2 抗高过载过程仿真分析
文献[1]给出了M795型号炮弹和我国某型号弹药的膛内过载曲线,其基本形式如图3所示,只是具体数值不同。钟形振子式角速率陀螺的分析重点也是针对于高过载环境,为考虑指标考核的通用性与一致性,同样采用图3中的曲线形式进行分析,只是将最大幅值调整为12500g。
在有限元仿真方法上,文献[1]利用LS-DYNA软件进行了动力学分析,钟形振子的结构和材料参照表1,固定约束条件与模态仿真约束一致。钟形振子的最大等效应力曲线如图4所示,其最大值为134.8MPa,出现在5.81ms,此时钟形振子承受的等效应力分布图如图5所示。根据屈服判定准则[4-6], 134.8MPa的最大等效应力远小于材料屈服强度,若考虑2倍的工况系数,269.6MPa的最大应力也远小于材料的屈服强度。因此,钟形振子在冲击过程中,仅处于弹性形变范围内,结构本身并未发生损坏。
在冲击过程中,钟形振子的最大矢量位移出现在钟唇上,变化曲线如图6所示,其最大位移为1.1nm。对于钟形振子而言,其振动本身的位移为10μm左右。故由高过载引发的位移对研究性能的影响可被控制在一定范围内,并可通过电路控制等手段,将该影响有效消除。

图3 过载约束载荷曲线Fig.3 Curve of overload constraint load

表1 钟形振子有限元仿真参数Table 1 Finite element simulation parameters of bell-shaped oscillator

图4 钟形振子最大等效应力曲线Fig.4 Maximum equivalent stress curve of bell-shaped oscillator

图5 t=5.81ms时钟形振子承受的等效应力分布图Fig.5 Equivalent stress distribution of bell-shaped oscillator when t=5.81ms

图6 钟形振子矢量位移曲线Fig.6 Vector displacement curve of bell-shaped oscillator
3 抗高过载特性与结构参数
对于钟形振子的结构参数与抗高过载特性的关系,重点分析结构参数本身,仿真参数如表2所示,仿真结果如图7所示。
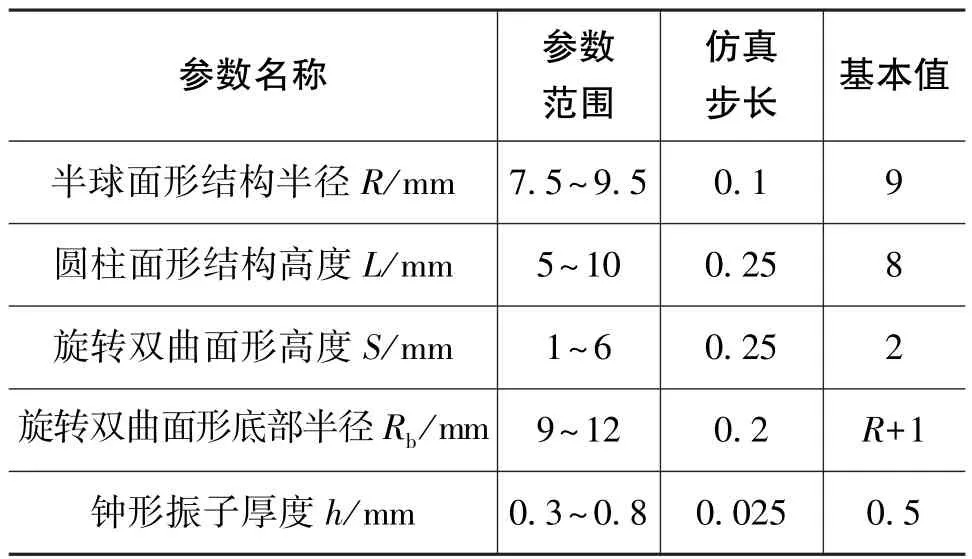
表2 结构参数仿真范围与步长Table 2 Simulation range and step size of structural parameters


图7 结构参数与最大等效应力关系Fig.7 Relationship between structural parameters and maximum equivalent stress
由图7可以看出,最大等效应力随着钟形振子厚度的增加而减小,随着剩余主要结构参数的增加而增加,且在变化过程中,均呈现出线性特征。利用线性回归方法,分析各结构参数与最大等效应力间的关系,得到的多元线性回归模型为

在回归分析中,计算得到的可决系数为0.988, 回归分析的p值均为 0.001<0.05, 故回归模型成立。由此可以看出,钟形振子厚度对钟形振子的抗高过载特性影响最大,其余影响因素依次为双曲面形底部半径、半球面形半径、圆柱面形高度和旋转双曲面形高度。
4 结论
针对极端瞬态力作用下金属壳谐振陀螺的结构强度进行了研究,在分析其工作原理和基本数学模型的基础上,利用有限元仿真方法,在通用炮射环境条件下进行了分析。通过仿真计算,给出了金属壳谐振陀螺的结构强度分析,验证了其抗过载能力。
