数列在购买彩票中的应用

冯水松

【摘 要】 本文阐述数列在彩票方面的两个原理：赌徒输光定律和倍投方法。

【关键词】 数列通项；赌徒输光定律；倍投方法

众所周知，数列是数学知识中的一个重要环节，以具体问题为基础，进行答案的解析是数列学习中的一个重要部分，这就注定了数列是以解决实际问题为目的而存在的。数列在经济生活和资源计算等领域，有着广泛的使用，本文将举例阐述数列在彩票方面的应用情况。

一、购买彩票能致富吗

购买彩票在人们的日常生活中经常遇到。概率论中有一个十分有趣的定律，在一次公平的游戏中（赢输的可能性各为0.5），任意一个游戏参与者都有可能会赢，谁赢了都是偶然的，但只要游戏一直进行下去，参与者输个精光却是必然的，这个定律又称赌徒输光定律。下面，我们用数列的方法来简单证明一下这个定律。

这样，我们得到了一个有点反直觉的结论：不管你的资金有多么雄厚，你用的可能性购买彩票，必然会输光。这也就是人们说的“久赌必输”。某些彩民会一次押多于1单位的量，认为这可以赢，但是不难看出来，这样只是改变了这些彩民购买彩票的方式，只要这个游戏属于都是的可能性，最后彩民总是要输得精光的。

二、倍投方法

倍投方法多用于公平的博彩游戏中，指的就是在前一次输了的情况下，再次投入前一次两倍的资金进行游戏。在资金足够多的情况下，这样成倍成倍地投入进去，只要是公平的游戏，总有机会赢，且一次就可以将前面所有输了的钱赢回来。

设某一个彩民的初始资金为a元，在公平的游戏中（赢输的可能性各为0.5），为便于讨论，我们假设彩票的结果只有两种，如购买大小，红黑，球队的胜负等。有什么方法保证彩民能赢钱呢？

有彩民这样认为：把初始资金a元按如下方式投注：1元、2元、4元、8元、16元、32元、64元……然后先押1元，输了的话，就押2元，再输，就押4元……这样一直下去，根据等比数列求和知识可以知道，只要能赢一次，就相当于把以前输过的钱全部赢回来并且还能赢得1元。之后再重新开始：1元、2元、4元……这样循环往复，每次就都能赚1元了。

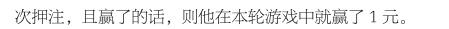
事實上，我们不难发现，在上面的假设下，要保证连输许多次之后仍然有充分的资金押注，就意味着彩民需要准备充分大量的初始资金。那彩民按这个倍投式策略：1元、2元、4元……的方式押注，赢1元回来，之后再重复，又赢1元回来；这样想，这个策略是可以的。但是问题是，在实际生活中，任何一个人的资金都不会是无限大的，他可能在连输n回之后就没有充分的资金进行押注了。

举一个最简单的例子，比尔盖茨的资产十分巨大，如果他用他所有的资产去博彩，相对于其他普通人来说，他拥有的数额巨大的资产让他可以选择使用倍投术博彩，并且可以承受比普通人大得多的风险，在这种情况下，他在博彩中可以用来使用倍投术的博彩次数也比普通人要多得多，这样的话，他也许就能盈利，但是这种盈利也只是暂时的，因为倍投术的前提是拥有无限的资金，而比尔盖茨的赌本虽然多，但是也不是无限的。这样就符合了赌徒输光定律的条件：有限的资金。虽然这资金很巨大，但是终究有限，这样下去，若是比尔盖茨一直进行下去，也终究会花光他的所有资产，这就是赌徒输光定律的结果。所以不管使用何种方法或者算法运用在博彩中，都只会带来短暂的盈利，不可能带来长久的巨大财富。切不可因为掌握了几种简单的方法就想运用在博彩上，而妄图发家致富。

【参考文献】

[1]理查德.威斯曼，赌场式交易策略[M].北京：机械工业出版社.

[2]李建标，李朝阳，刘桂林，徐赛，随机决策的收益：赌徒谬误还是热手效应？——基于仿真实验研究.第五届中国管理学年会（MAM2010），2010.

[3]刘庆顺，王刊良，动态决策过程中备选项的序列特征效应研究，第十届全国青年系统科学与管理科学学术会议论文集.

[4]闻人王冠.澳门病态赌徒的赌博行为特点及其影响研究[D].华南师范大学，2008.