地铁盾构通用环管片楔形量计算方法研究
2019-06-11张稳军朱战魁高树东董秀竹
张稳军, 朱战魁, 张 琪, 高树东, 董秀竹
(1. 天津大学建筑工程学院, 天津 300354; 2. 天津大学 滨海土木工程结构与安全教育部重点实验室, 天津 300354; 3. 天津滨海新区轨道交通投资发展有限公司, 天津 300459;4. 中国铁路设计集团有限公司, 天津 300142)
0 引言
近年来,随着我国城镇化水平的不断提高与城市人口的不断上升,城市轨道交通得以飞速发展。盾构法因其安全快捷、施工环境好、对周围环境影响小、地层适应性广、工程质量高等优越的工艺特点和较高的技术经济性,在城市地铁隧道建设中得到广泛应用。地铁盾构隧道由预制装配式管片拼装构成,管片设计不当易出现线路拟合偏差过大、管片破损、错台等病害,直接影响隧道的成型质量、后期运营和耐久性[1-3]。目前,我国地铁盾构隧道主要通过标准环+左转弯环+右转弯环和通用环2种管片组合形式来拟合隧道设计路线。其中,通用环管片在整条线路上只有一种管片形式,具有通用性强、线路控制精准以及易于纠偏等优点,近年来在宁波、武汉、兰州、天津等城市的地铁盾构隧道中得到了广泛应用,正逐渐成为主要的设计选择[4-5]。楔形量的大小会影响通用环管片线路拟合和施工纠偏的能力,是该类管片的关键设计参数之一。
针对管片楔形量的计算,GB 50157—2013《地铁设计规范》指出管片楔形量应根据线路最小曲线半径计算,并留有满足最小曲线半径段的纠偏等施工要求的余量[6]; GB 50446—2017《盾构法隧道施工及验收规范》指出管片楔形量应根据管片种类、管片宽度、管片外径、曲线半径和管片制作的方便性等计算确定[7];姚德宁等[8]、刘凤华[9]、宋成辉[10]、张忠桢等[11]、小泉淳[12]给出了4种管片楔形量的计算方法;吕延豪[13]通过分析不同楔形量通用管片对应设计线路中不同曲线和直线的拟合误差,对武汉地铁通用管片楔形量进行了研究。然而,目前国内关于地铁盾构通用环管片设计时应该采用哪种计算方法设计楔形量没有形成统一的理念。此外,以往研究地铁盾构通用环管片楔形量时一般仅考虑满足线路平面拟合偏差的控制要求,忽略了对线路高程拟合偏差的控制; 但是不同通用环管片楔形量计算方法都是基于线路平面曲线得到的,没有体现线路竖直方向的拟合情况,而线路平面曲线部分竖曲线一般是带有坡度的直线,高程起伏可达数十m,线路高程拟合偏差可能已达到控制限值。同时,以往研究地铁盾构通用环管片楔形量时,分析不同楔形量通用管片对单一平面线形或竖曲线拟合能力的较多,忽略了不同线形交界处初始偏差及管片走向对后续管片拼装的影响,容易导致确定的管片楔形量不适用于连续复杂线路的区间。因此,有必要综合考虑通用环管片线路高程拟合情况,系统分析不同楔形量通用环管片对连续复杂线形区间的拟合能力,明确地铁盾构通用环管片楔形量的计算方法。
本文首先对类似通缝、紧邻交错、非对称间隔交错和对称间隔交错4种计算通用环管片楔形量计算方法进行介绍与比较; 其次结合天津市滨海新区轨道交通Z2线管片设计资料,对几种楔形量计算方法的线路高程拟合结果进行分析,并对Z2线典型区间的通用环管片楔形量进行计算; 最后提出综合考虑通用环管片线路高程拟合情况的地铁盾构通用环管片楔形量多层次控制设计流程。
1 管片超前量的计算
通用环管片通过有序旋转和组合拼装形成盾构隧道,可以适用于不同曲率半径的隧道,并可用于直线段、左转弯段、右转弯段和竖曲线段等工况。通用环管片拼装时,K块管片位于不同拼装点位,其左部、右部、上部及下部的超前量,即管片沿纵断面方向上的长度相对管片前后端面两中心点长度的差值,也相应发生变化。根据文献[14]的相关结论,不同拼装点位管片的超前量可按式(1)计算。
(1)
式中:δ为管片超前量,mm;Δ为管片楔形量,mm;θ为通用环拼装角度,(°)。
一般通用环在起拱线处设定最大宽度与最小宽度。在管片拼装中,为了进行错缝拼装,K块管片会有一定的拼装角度θ,因此,水平方向实际有效的楔形量为Δ·cosθ,竖直方向的楔形量为Δ·sinθ。
2 通用环管片楔形量计算方法
通常一条地铁隧道线路上有很多不同半径的曲线,如按不同的曲线半径来设计通用环管片楔形量,会造成类型太多,并给制造、设计和施工增加工作量。因此,常用的方法是根据线路最小曲线半径,同时综合考虑管片拼装方式、管片外径、管片环宽,按照几何相似关系确定一种通用环。
(2)
式中:Rmin为线路最小曲线半径,mm;D0为管片外径,mm。
曲线半径与楔形量之间的关系如图1所示。
目前,有4种计算通用环管片楔形量的方法,分别为类似通缝计算方法、紧邻交错计算方法、非对称间隔交错计算方法和对称间隔交错计算方法,其中,类似通缝计算方法使用最多。

图1 曲线半径与楔形量Fig. 1 Curve radius and taper
2.1 类似通缝计算方法
计算地铁盾构通用环管片楔形量时常采用如图2(a)所示的计算图示,将前后两衬砌环的K块从基准状态的通用环,即通用环拱腰处分别对应最大环宽与最小环宽,前后交错错开2个拼装点位。由式(1)可得,衬砌环外弧长度和内弧长度始终不变。此外,图2(a)还满足管片错缝拼装要求,并且能够避免出现疑似通缝。
类似通缝计算方法即采用如图2(a)所示的计算图示,但该方法在计算地铁盾构通用环管片楔形量时不考虑管片错缝拼装的影响。能满足通缝拼装需要的管片楔形量由式(3)计算得到。
(3)
式中B为管片环宽,mm。
2.2 紧邻交错计算方法
紧邻交错计算方法计算地铁盾构通用环管片楔形量时采用如图2(b)所示的计算图示,将前后两通用环的K块从基准状态的通用环无间隔交错错开1个拼装点位。该方法可由式(4)计算管片楔形量。
(4)
式中α为相邻拼装点位之间的夹角,(°)。
2.3 非对称间隔交错计算方法
非对称间隔交错计算方法计算地铁盾构通用环管片楔形量时采用如图2(c)所示的计算图示,将前后两通用环的K块从基准状态的通用环向同一方向交错错开2个拼装点位。该方法可由式(5)计算管片楔形量。
(5)
2.4 对称间隔交错计算方法
对称间隔交错计算方法计算地铁盾构通用环管片楔形量时,采用与类似通缝计算方法相同的计算图示。该方法考虑了管片错缝拼装对实际楔形量的影响,可由式(6)计算管片楔形量。
(6)
2.5 4种通用环管片楔形量计算方法比较
类似通缝、紧邻交错、非对称间隔交错和对称间隔交错4种计算方法都是为了计算通用环管片楔形量。4种计算方法之间的比较如表1所示。

(a) 类似通缝计算方法和对称间隔交错计算方法计算图示

(b) 紧邻交错计算方法计算图示

(c) 非对称间隔交错计算方法计算图示

计算方法 计算依据相邻两环拼装点位错开数量/个错缝拼装疑似通缝楔形量计算结果类似通缝计算方法通缝拼装2是无最小紧邻交错计算方法错缝拼装1是有第3非对称间隔交错计算方法错缝拼装2是无最大对称间隔交错计算方法错缝拼装2是无第2
由表1可得,采用紧邻交错计算方法排列通用环管片时存在疑似通缝,而疑似通缝的存在会改变管片的力学状态,这与设计阶段采用的计算模型不符,通用环管片实际拼装时也往往限制多环管片连续出现疑似通缝。因此,不宜采用紧邻交错计算方法计算通用环管片楔形量。
比较类似通缝计算方法、非对称间隔交错计算方法和对称间隔交错计算方法可以看出,3种方法均满足管片错缝拼装要求,并且能够避免出现疑似通缝。相同条件下非对称间隔交错计算方法楔形量计算数值偏大,如按国内地铁盾构通用环管片环与环之间常用的16个纵向螺栓连接计算,非对称间隔交错计算方法计算得到的楔形量是类似通缝计算方法的1.17倍,是对称间隔交错计算方法的1.08倍,这会减小楔形量的选择范围,不利于选用最优的楔形量。因此,也不宜采用非对称间隔交错计算方法计算通用环管片楔形量。
此外,类似通缝计算方法在计算管片楔形量时没有考虑管片错缝拼装对实际楔形量的修正,理论假设存在不足。相比而言,对称间隔交错计算方法修正了管片错缝拼装对实际楔形量的影响,在计算管片楔形量时更符合实际,而且计算得到的管片楔形量偏小,有利于增加楔形量的选择范围,并利于选用最优的楔形量。因此,在计算通用环管片楔形量时应优先考虑使用对称间隔交错计算方法。考虑到类似通缝计算方法与对称间隔交错计算方法采用的计算图示相同,并且在计算通用环管片楔形量时后者优于前者,后面将不再对类似通缝计算方法进行分析。
3 几种楔形量计算方法的线路高程拟合结果比较
3.1 工程概况
天津市滨海新区轨道交通Z2线工程位于天津市滨海新区内,是滨海新区轨道交通网络中的重要组成部分,该工程线路平面最小曲线半径为350 m。Z2线地下线部分采用盾构法修建,衬砌采用平板型单层预制钢筋混凝土通用环管片。管片初步设计参数如表2所示。管片拼装点位如图3所示。

表2 管片初步设计参数

图3 管片拼装点位示意图Fig. 3 Sketch of assembling points of segment
3.2 线路高程拟合结果与分析
为分析上述紧邻交错计算方法、非对称间隔交错计算方法和对称间隔交错计算方法拟合线路高程的适用性,基于Z2线管片设计资料建立三维实体通用环模型,根据楔形量计算方法的原理对管片进行人工排版。排版后的线路高程拟合结果如图4所示。
由图4可以得出: 通用环紧邻交错22.5°排列时,拟合高程增大比较明显,呈现每环高程增量比上环增量大1.72 mm的规律,在拼装到第6环时,高程变化超过20 mm,随着通用环的不断拼装,高程不断增大,在拼装到第8环时,高程达到48 mm;采用非对称间隔交错45°排列时,拟合高程增大更加明显,每环高程增量比上环增量大3.18 mm,在拼装到第4环时,高程变化已非常接近20 mm,在拼装到第8环时,高程达到89 mm;采用对称间隔交错45°排列时,拟合高程几乎没有增加,在拼装到第8环时,竖向拟合高程仍然很小。
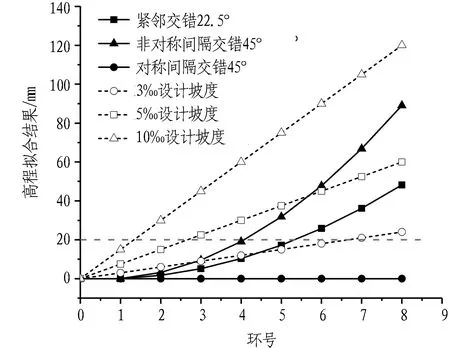
图4 线路高程拟合结果Fig. 4 Results of elevation fitting of DTA
紧邻交错计算方法和非对称间隔交错计算方法的线路拟合高程增大明显是因为这2种方法始终向同一方向偏转,使得垂直方向的坡度不断增大,高程逐环增大; 而对称间隔交错计算方法通过上下交错组合通用环使得垂直方向的坡度在2环内相互抵消,平均坡度很小。因此,对称间隔交错计算方法的线路高程变化很小。
为分析3种计算方法与隧道设计轴线的高程拟合偏差,对隧道设计轴线坡度分别为3‰、5‰和10‰的高程变化情况进行计算。
分析3种计算方法的线路高程拟合结果与隧道设计轴线不同坡度的高程变化情况,可以得到: 实际线路不同坡度的高程变化随管片环数的增加均近似呈线性增加,而按紧邻交错计算方法和非对称间隔交错计算方法采用单一的方式交替排列通用环时,线路拟合高程呈非线性增加; 同时对称间隔交错计算方法的线路高程变化很小,与实际线路高程变化均存在较大差异。仅以单一的管片组合方式拟合线路时,线路高程拟合偏差很快会达到控制限值,难以拟合实际线路。如按对称间隔交错计算方法采用单一的管片组合方式拟合设计坡度为3‰的隧道轴线,在拼装到第7环时高程拟合偏差已达到20 mm,并且随着拼装环数的增加,拟合偏差越来越大,无法长距离拟合实际线路。
综上,通用环管片拟合隧道设计轴线应当是多种管片拼装方式组合的结果,设计通用环管片楔形量时有必要验证由上述计算方法计算得到的管片楔形量是否满足控制要求,并且在验算时线路高程拟合偏差是一项重要的控制因素。
4 通用环管片楔形量计算流程
4.1 管片楔形量的计算
为确定适用于Z2线的通用环管片楔形量,考虑需要满足施工纠偏等要求的余量,采用对称间隔交错计算方法根据式(6)计算不同曲线半径的楔形量,如表3所示。选取含有最小曲线半径段、具有5个平面曲线段和线路长达3 585 m的典型区间南淀公园站—空港经济区站,该区间设计线路参数如表4和表5所示。采用同济曙光“盾构隧道管片排版选型软件”对上述楔形量进行分析研究,并在分析时对初步设计附近的楔形量进行适当加密,拟合排版后的结果如表6所示。

表3 曲线半径与楔形量Table 3 Curve radius and tapers

表4 竖曲线参数Table 4 Parameters of vertical curve
分析表6可以得到,按照最小曲线半径计算得到的管片楔形量并不能实现线路拟合排版,满足适用于线路拟合要求的管片楔形量主要分布在比线路最小曲线半径小50~100 m的范围内,并且集中分布在比线路最小曲线半径小80 m的曲线半径附近。
初步设计选定的管片楔形量39.6 mm虽然可以完成管片排版,并且比该楔形量附近其他楔形量的拟合排版结果较好,但是仍然有11环管片平面拟合偏差超过了20 mm的偏差控制要求; 而且其拟合排版结果次于楔形量为40 mm和42 mm的拟合结果,不是最优的管片楔形量。

表5 平面曲线参数Table 5 Parameters of plane curve

表6 拟合排版结果Table 6 Results of segment layout
注: 1)GB 50446—2017《盾构法隧道施工及验收规范》指出,地铁隧道施工轴线与设计轴线偏差应控制在50 mm以内。2)管片设计排版时一般要求隧道拟合轴线与设计轴线的偏差整体不应大于10 mm,局部不应大于20 mm[9, 13]。3)×表示不适用; △表示一般适用; ○表示较适用; ◎表示非常适用。
在分析的所有楔形量中,楔形量为40 mm时的线路拟合结果最好,此时所有管片环均满足拟合偏差控制要求,而且制作管片时40 mm的楔形量也比39.6 mm更容易控制精度。因此,建议对40 mm的楔形量进行整体分析,研究该楔形量的适用性。
从楔形量37.0 mm比38.0 mm线路拟合结果好,以及楔形量为44.0 mm比39.6、40、41、42 mm线路拟合结果差可以看出,虽然理论上管片楔形量越大,能够拟合的最小曲线半径越小,但是并不是管片楔形量越大线路拟合效果越好。因此,有必要在确定管片楔形量时进行管片设计排版,在初步选定的楔形量附近进行加密研究,选定最合适的楔形量。
从拟合偏差结果可以看出,相比于线路平面拟合偏差,高程拟合偏差一般偏小,但是仍有个别通用环的最大高程拟合偏差超过了10 mm,可能受本区间线路竖曲线线形的影响,高程拟合偏差没有成为主要的控制因素,但不能排除在其他线形中高程拟合偏差不起控制因素。因此,仍有必要在通用环管片楔形量设计时综合考虑高程拟合偏差。
4.2 通用环管片楔形量设计流程
通过上述分析可以看出,有必要在施工前根据隧道设计轴线的走向和通用环管片的几何特征,对管片进行设计排版,以检验选定的管片楔形量是否满足控制要求。
此外,选定管片楔形量时,以往工程管片楔形量的使用经验也是重要的选择依据。总结过去的使用经验,对于地铁盾构隧道,常用管片楔形量的范围如表7所示。

表7 常用管片楔形量范围值[15-16]
基于本文的相关结论,通用环管片楔形量可以通过如下步骤确定:
1)采用对称间隔交错计算方法根据式(6)分别计算将线路最小曲线半径折减50、70、80、90、110 m对应的初步设计楔形量;
2)根据隧道设计轴线的走向和通用环管片的几何特征对管片进行设计排版,判断楔形量是否满足平面和高程拟合偏差控制要求;
3)当楔形量不满足线路平面或高程拟合偏差控制要求时,可以考虑以往楔形量的使用经验将其适当增减,或在线路拟合偏差最小的楔形量附近以1~2 mm为增量进行加密研究,重新设计楔形量,以满足线路拟合偏差控制要求;
4)当选定的楔形量同时满足线路平面和高程拟合偏差控制要求时,在线路拟合偏差最小的楔形量附近以1 mm为增量进行加密研究,验算附近的楔形量是否也满足线路拟合偏差控制要求,以判断是否存在更合适的楔形量;
5)根据通用环管片楔形量是否留有满足施工纠偏等要求的余量及管片制作的方便性2个因素选取最终的楔形量。
通用环管片楔形量设计流程如图5所示。通过该流程可以用于计算单洞单线地铁盾构隧道通用环管片初步设计和施工设计阶段的楔形量。
5 结论与讨论
本文主要对地铁盾构通用环管片楔形量计算方法进行研究,通过结合天津市滨海新区轨道交通Z2线管片设计资料,对几种楔形量计算方法进行对比分析,提出综合考虑通用环管片线路高程拟合情况的地铁盾构通用环管片楔形量多层次控制设计流程,明确地铁盾构通用环管片楔形量的计算方法,并系统分析不同楔形量通用管片对Z2线连续复杂线形区间的拟合能力,可为该工程管片楔形量的确定提供参考,也可为今后类似工程地铁盾构通用环管片楔形量的设计提供计算依据和参考。
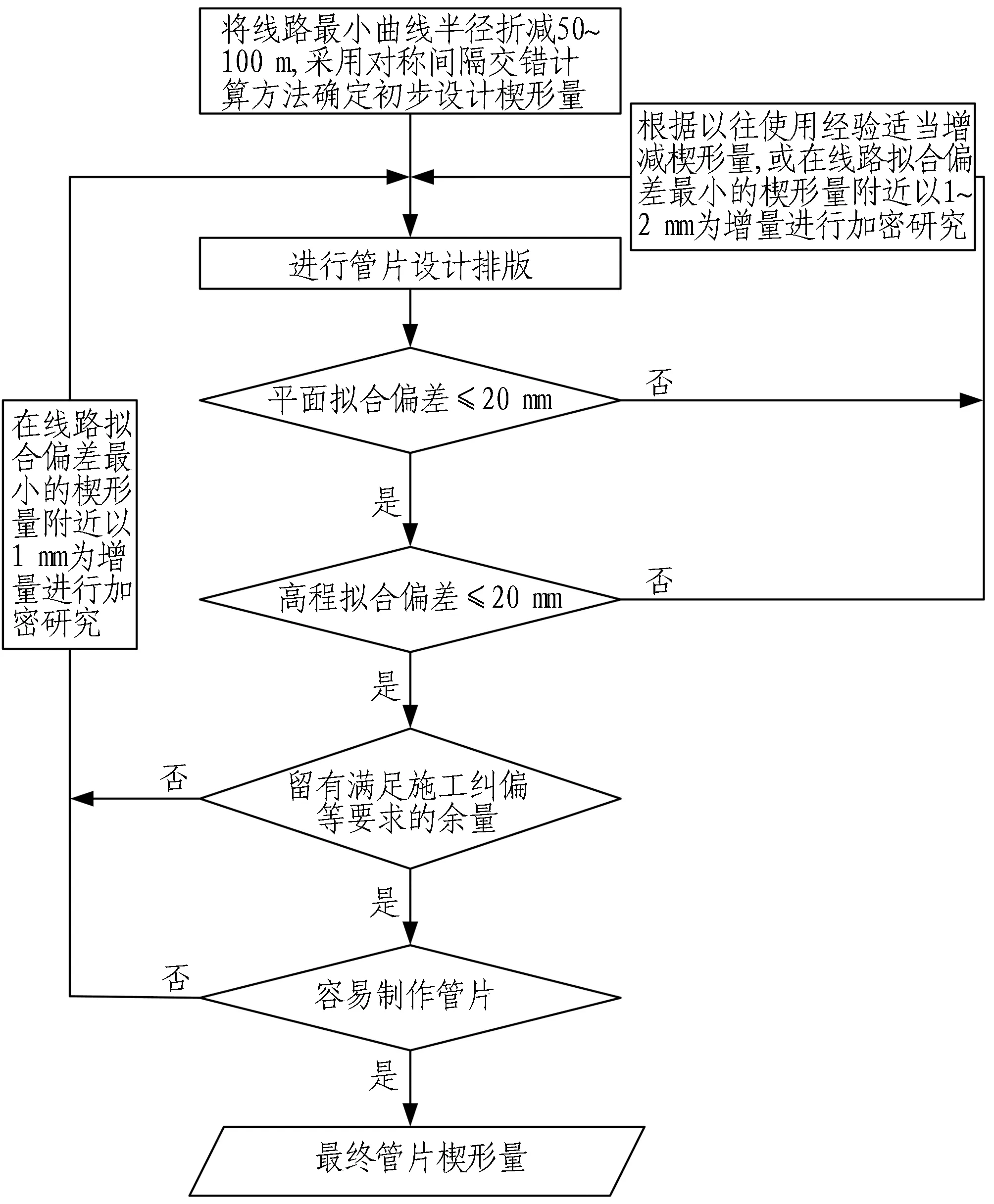
图5 通用环管片楔形量设计流程
Fig. 5 Design flowchart of taper calculation of universal ring segment
1)相比于类似通缝、紧邻交错和非对称间隔交错计算方法,对称间隔交错计算方法更适用于计算通用环管片楔形量。
2)在确定通用环管片的初步设计楔形量时,根据最小曲线半径计算得到的管片楔形量往往不能实现线路拟合排版,将最小曲线半径折减50~100 m确定初步设计的楔形量,可以简化楔形量的设计过程。
3)仅以单一的管片组合方式拟合线路时,线路高程拟合偏差容易超过控制要求,设计通用环管片楔形量时有必要验证计算得到的管片楔形量是否满足控制要求,并且在验算时线路高程拟合偏差是一项重要的控制因素。
4)管片楔形量越大,对应的线路拟合效果并不是越好,有必要在初步选定的楔形量附近根据以往的使用经验适当增减楔形量,或在线路拟合偏差最小的楔形量附近进行加密研究,以优化通用环管片的楔形量。
