基于代理模型的碾压混凝土坝坝体渗控结构多目标优化

程正飞，王晓玲，任炳昱，吕 鹏，余红玲



基于代理模型的碾压混凝土坝坝体渗控结构多目标优化

程正飞，王晓玲，任炳昱，吕 鹏，余红玲

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

针对现有碾压混凝土坝坝体渗控结构优化研究中常用的单目标、单参数的优化方法难以获得同时满足多个目标要求的渗控结构设计方案，无法充分考虑不同设计参数之间的关联性以及计算效率低的不足，提出了基于代理模型的碾压混凝土坝坝体渗控结构多目标优化方法．其主要包括：①建立以渗控结构设计参数为设计变量，以防渗层最大水力梯度、溢出点高程以及渗控结构造价为优化目标的碾压混凝土坝坝体渗控结构多目标优化数学模型；②提出基于多目标粒子群算法与代理模型的模型求解方法，其中多目标粒子群算法应用于快速求解Pareto解集，而代理模型应用于建立设计参数与优化目标之间的近似关系式，用以替代优化过程中求解耗时的渗流数值模型，从而提高求解效率，同时考虑不同设计参数之间的关联性．利用本文方法对某碾压混凝土坝坝体渗控结构进行多目标优化，并通过与传统方法进行对比验证了该方法的有效性与优越性．

碾压混凝土坝坝体；渗控结构；多目标优化；代理模型；多目标粒子群算法

碾压混凝土(roller-compacted concrete，RCC)坝坝体的成层特性，导致其存在众多渗流薄弱面，使得渗流问题成为影响碾压混凝土坝坝体安全稳定的一大因素[1]．为了减小渗流对碾压混凝土坝坝体安全稳定的不利影响，工程中通常会在坝体中布置渗控结构．然而，由于碾压混凝土坝坝体的特殊性以及渗流问题的复杂性，使得根据工程经验设计的渗控结构常常难以达到理想的渗控效果．因此，进行渗控结构优化研究对于有效地控制碾压混凝土坝坝体渗流具有十分重要的理论与实践意义．

国内外许多学者开展了碾压混凝土坝坝体渗控结构设计与优化相关研究．朱岳明等[2-4]系统地比较了各种碾压混凝土坝坝体渗控结构型式的优缺点，并总结出既能满足渗控要求、又利于快速施工的高碾压混凝土坝坝体渗控结构型式．崔皓东等[5]以光照高碾压混凝土重力坝为依托，通过对渗控结构的设计参数分别进行敏感性分析，得到施工简单且适应200m级高水头、高渗压的碾压混凝土坝坝体渗控结构优化型式，对类似工程具有一定的参考价值．黄蓓等[6]基于对碾压混凝土坝坝体渗控结构的抗渗性分析，采用自行设计的试验装置，测定了不同拉应力情况下二级配碾压混凝土的渗透性．李明超等[7]采用数值模拟和敏感性分析方法对碾压混凝土坝坝体“变态混凝土-二级配碾压混凝土”渗控结构的二级配碾压混凝土厚度、变态混凝土厚度以及渗控结构型式进行了优化设计．Li等[8]为了减小碾压混凝土坝坝体防渗层的振捣对施工进度的干扰，采用了一种高流动性的、防渗抗裂的免振捣混凝土作为防渗层材料，并且通过实验验证了这种防渗层的有效性．

从以往研究可知，现有碾压混凝土坝坝体渗控结构优化研究大多结合数值模拟与敏感性分析采用单目标、单参数的优化方法，即首先根据工程运行条件和以往工程经验，拟定一个渗控结构设计方案，利用数值模拟对其渗控效果进行评价；然后根据渗控效果的评价结果确定需要进行优化的渗控结构设计参数(例如防渗层厚度、排水孔孔距等)；最后以某一渗流安全性指标(例如渗流量、扬压力等)为优化目标，采用敏感性分析方法对需要优化的渗控结构设计参数逐一进行优化，从而得到渗控结构优化设计方案．一般情况下，这种方法得到的渗控结构设计方案基本可以满足工程要求．然而，这种方法存在两个较为明显的不足：①该方法通常以单个渗流安全性指标为优化目标，难以得到同时满足多个目标要求的渗控结构设计方案；②该方法对多个渗控结构设计参数的优化是逐一、独立地进行的，无法充分考虑不同参数之间的关联性，并且由于需要进行多次数值模拟试验，使得其计算效率较低．为克服传统优化方法的不足，少数学者[9-11]对重力坝坝基、渠道等工程的渗控结构开展了一些多目标或者多参数联合的优化研究，但是尚存在求解精度较差或者求解效率较低等问题．

为了均衡多目标优化问题的求解精度与求解效率之间的矛盾，许多学者通过引入代理模型技术为快速求解多目标优化问题提供新的途径[12-15]．代理模型是指能够大幅度简化计算过程，极大地降低计算成本，而且计算结果与物理试验或者数值计算的结果非常相近的近似数学模型[16]．通过构建代理模型近似模拟输出量与输入量之间的关系，一方面可以替代计算耗时的物理试验或者数值模拟，另一方面可以将多个输入量利用显式表达式联系起来．代理模型在船舶、汽车、航空等行业的流体分析、结构设计以及多学科优化设计等方面得到广泛应用与快速发展[17].近年来，代理模型逐渐被引入到水利水电工程相关领域，特别是在参数敏感性分析、不确定性分析及参数识别与优化等方面[18]，然而目前尚未被应用于大坝渗控结构优化研究当中．

针对现有研究的不足，本文开展考虑多目标、多参数的碾压混凝土坝坝体渗控结构优化研究，需要解决以下两个方面问题：①如何建立兼顾渗控结构优化过程中多个目标的数学模型以及提出相应的求解方法；②如何高效地对多个渗控结构设计参数进行联合优化．首先，针对问题1，依据多目标优化理论，建立碾压混凝土坝坝体渗控结构多目标优化数学模型，并引入多目标粒子群算法进行求解；其次，针对问题2，构建渗控结构设计参数与优化目标之间的代理模型，一方面，通过代理模型将多个渗控结构设计参数联系起来，进而在优化过程中考虑它们之间的关联性，另一方面，采用代理模型替代计算耗时的渗流数值模型，进而提高求解效率；然后，给出了基于代理模型的碾压混凝土坝坝体渗控结构多目标优化求解流程；最后，对某碾压混凝土坝坝体渗控结构进行多目标优化，获得Pareto解集，并采用逼近理想排序(TOPSIS)法对Pareto解集进行排序，从而得到最终优选渗控结构设计方案．

1 研究框架

根据碾压混凝土坝坝体渗控结构的特点建立相应的多目标优化数学模型，采用耦合代理模型的多目标粒子群算法进行求解，进而对碾压混凝土坝坝体渗控结构进行多目标优化，研究框架如图1所示，分别为多目标优化数学模型的建立、数学模型的求解以及方法的实际应用，主要包括以下内容：

(1) 根据工程勘测设计资料和以往工程经验，对碾压混凝土坝坝体渗控结构优化空间进行分析，确定需要优化的设计参数(防渗层厚度、排水孔孔距等)与它们的取值范围、优化目标(安全性，经济性等)以及约束条件(容许值)，进而建立碾压混凝土坝坝体渗控结构多目标优化数学模型．

(2) 运用多目标粒子群算法求解数学模型，并在求解过程中采用代理模型替代计算耗时的渗流数值模型，一方面提高计算效率，另一方面充分考虑不同设计参数之间的关联性．若迭代计算很多次后仍不收敛，则需要对目标函数或者优化算法进行改进；若收敛，则得出Pareto解集，并根据工程实际需要从中选出一组解作为最优解．

(3) 将研究方法应用于实际工程，实现对碾压混凝土坝坝体渗控结构的多目标优化，并通过对比分析验证该方法的有效性．

图1  研究框架

2  碾压混凝土坝坝体渗控结构多目标优化数学模型

碾压混凝土坝坝体对于渗控结构的要求主要是：安全可靠，且具有很好的耐久性；能有效地控制渗漏量和降低扬压力；造价合理，施工便捷．从多目标优化的角度出发，碾压混凝土坝坝体的渗控结构优化应该使得其安全性与经济性皆优，即工程渗流安全性态较好且渗控结构造价较低[19]．

对于碾压混凝土坝坝体的渗控结构优化，安全性主要涉及防渗层渗流安全和坝体整体渗流安全．防渗层渗流安全采用防渗层的最大水力梯度作为量化指标，其越小越安全．坝体整体渗流安全通常采用溢出点高程和坝体渗流量作为量化指标，两者均越小越安全[7]；由于坝体渗流量与溢出点高程一般成正相关关系，即溢出点高程越高，坝体渗流量越大，所以本文选择将溢出点高程作为优化目标函数，而将坝体渗流量作为约束条件．经济性主要是指渗控结构的造价，其越小越经济．因此，选取防渗层最大水力梯度、溢出点高程以及渗控结构造价作为碾压混凝土坝坝体渗控结构多目标优化的目标函数，建立相应的数学模型如式(1)所示．

Opt(，，) (1)

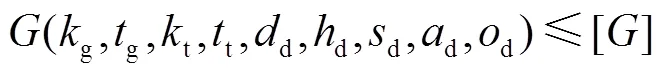
3 模型求解方法

3.1 Pareto解集的概念

在大多情况下，多目标优化问题中的各个子目标存在相互冲突的关系，难以找到一个解使得所有子目标同时达到最优；因此，在求解多目标优化问题时，只能对各个子目标进行协调和折中处理，尽量使它们均接近最优．法国经济学家Pareto最早研究了经济学领域内的多目标优化问题，并提出了Pareto解集，即非劣最优解集．Pareto解集中的每个解仅仅是一组可以接受的较优解，并且一个多目标优化问题通常会有很多组较优解[20]．在实际应用中，需要根据实际需求与决策者的个人偏好，从Pareto解集中挑选一组或者几组解作为最优解．因此，求解Pareto解集是解决多目标优化问题的关键．

目前应用于求解Pareto解集的方法主要包括评价函数法、分层序列法、目标规划法等传统优化方法以及进化算法、粒子群算法、蚁群算法、模拟退火算法等智能优化算法[21]．其中，粒子群(PSO)算法是近年来一种新兴起的优化算法，由于其能够适应各类性质和形式的优化目标函数，可以求解各种复杂的优化问题，并且具有快速性、有效性和鲁棒性等多种优点，因而得以被广泛应用[22]．

3.2  粒子群算法

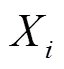
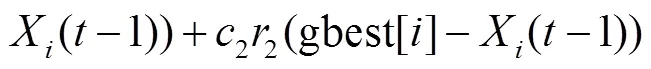
粒子群算法在求解单目标优化问题时具有非常良好的性能，但是难以直接用于求解多目标优化问 题[24]．为采用粒子群算法求解多目标优化问题，需要对其进行变异操作，进而提高解的多样性，增强粒子的全局搜索能力[25]．多目标粒子群优化(MOPSO)算法可通过对传统粒子群算法采用以下变异策略得到：当所有粒子的速度均小于某一限定值时，在一定范围内随机更改一些粒子速度上某些维的值，从而增强粒子的全局搜索能力；此外，由变异产生的优异粒子能够吸引到其他粒子，从而避免这些粒子陷入局部最 优[26]．具体变异操作为

3.3  代理模型

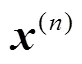
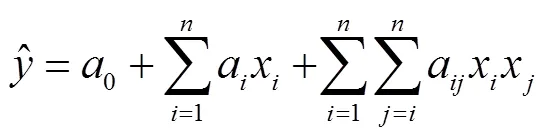
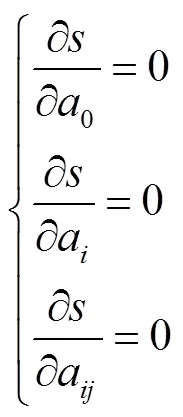
通过求解式(8)可以获得输入参数和输出结果之间的近似关系式(6)中各待定系数的估计值，进而得到响应面模型的显式表达式．

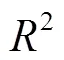
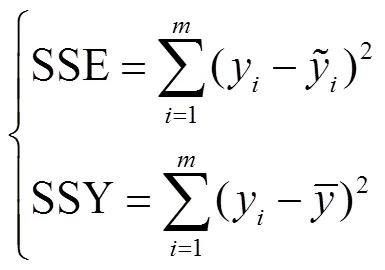
在0到1之间进行变化，如果越接近于1，则表示代理模型的拟合精度越高，但是，复相关系数仅能表示代理模型对于构建模型使用的样本点的拟合效果．因此，还需要随机抽取样本点外的误差分析点，分别计算它们的正演值与响应估计值，然后利用相对误差(RE)表示额外误差分析点的拟合精度，相对误差越小，拟合精度则越高，其表达式为

3.4 耦合代理模型的碾压混凝土坝坝体渗控结构多目标粒子群优化算法

采用多目标粒子群算法求解碾压混凝土坝坝体渗控结构优化问题时，需要调用成百上千次的渗流数值模型，可能导致耗费几天甚至数周的计算时间，严重影响优化效率[12]．为了克服这一问题，本文提出了耦合代理模型的碾压混凝土坝坝体渗控结构多目标粒子群优化算法，包括构建代理模型和粒子群多目标优化两部分内容，具体实施流程如图2所示，主要包括以下步骤．

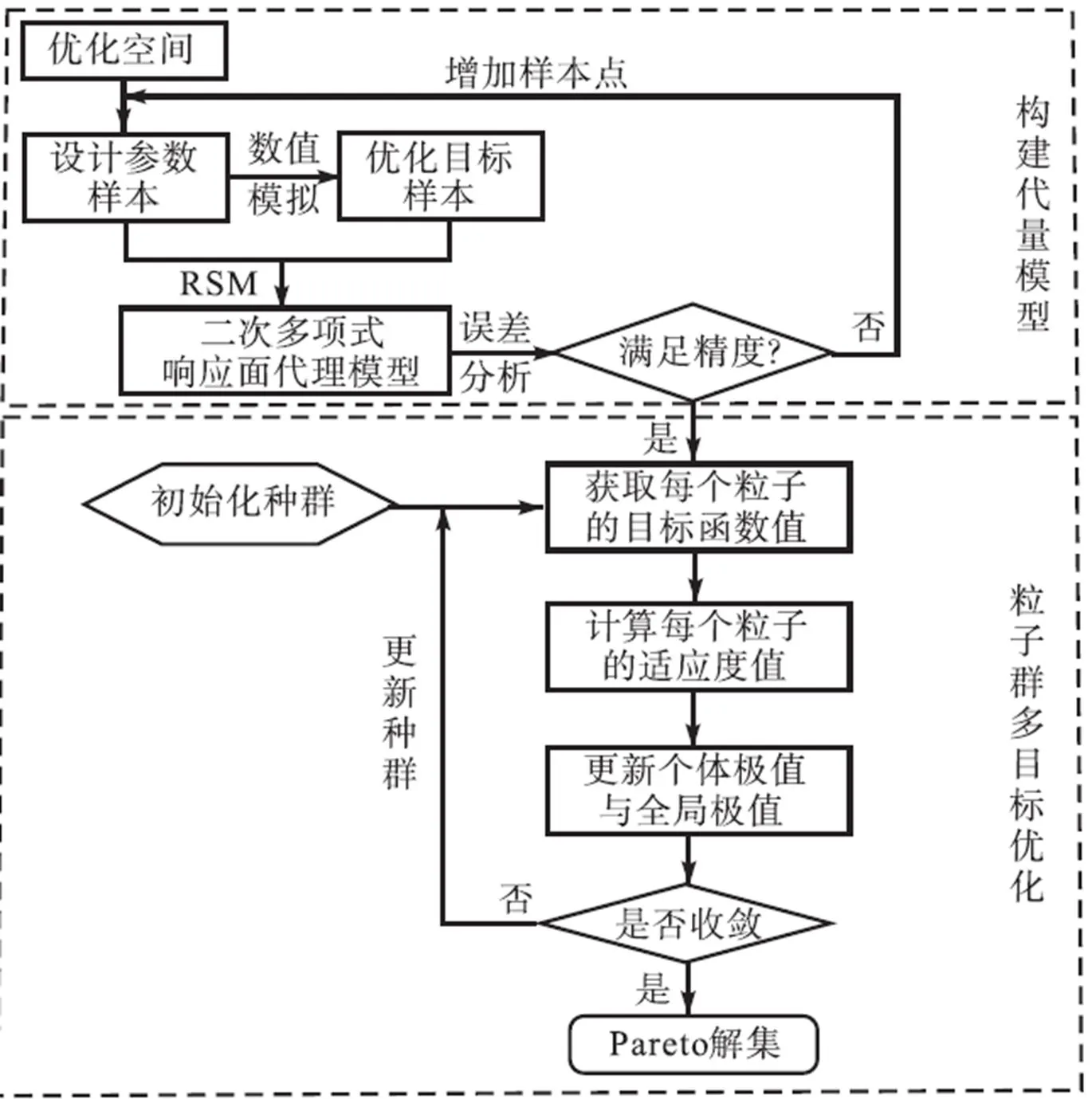
图2  多目标优化求解流程

步骤1采用拉丁超立方抽样(LHS)方法从设计参数空间内抽取样本点，并将这些样本点逐个输入到可靠的碾压混凝土坝渗流数值模型中进行数值模拟，得出样本点对应的优化目标样本数据集．

步骤2由样本点和优化目标样本数据集建立各个优化目标关于设计参数的多项式响应面代理模型.

步骤3对建立的代理模型进行误差分析，若不满足要求，则需要增加样本点，重新建立代理模型；若满足要求，则进入下一步．

步骤4初始化种群中各个粒子的位置和速度，并设置群体大小、惯性权重、加速度系数和迭代次数等参数值．

步骤5采用步骤1～步骤3建立的代理模型计算各个粒子的目标函数值，然后，计算各个粒子的适应度值，并把非支配解存储到外部存档中．

步骤6根据式(2)～式(5)更新各粒子的位置和速度，重新计算各个粒子的适应度值，进而更新它们的个体极值、全局极值以及外部存档．

步骤7以所得粒子是否接近全局最优解作为收敛条件，若未达到收敛，对种群进行更新，并返回步骤5；若收敛，得出Pareto解集．

4  工程应用

某碾压混凝土坝工程是位于我国西南地区的一等大(1)型水电工程．水库正常蓄水位、坝顶高程以及最大坝高分别为1134m、1139m与158m．以该工程的厂房坝段坝体为研究对象，其三维模型如图3所示，主要包括坝体内部三级配碾压混凝土区、上游面二级配碾压混凝土防渗层、下游面常态混凝土防渗层、坝顶及坝底常态混凝土区、坝体排水孔、廊道等 6个部分．

图3  厂房坝段坝体模型

坝体初始渗控方案为“二级配碾压混凝土防 渗＋坝体排水”，如图4所示．在坝体上游面布置二级配碾压混凝土层作为防渗层，其厚度沿高程呈阶梯状，从上端的4m变化至下端的8m，平均厚度约为6m；在坝体下游面的较低高程处采用常态混凝土薄层作为防渗结构；在坝体内部设置廊道和排水孔，排水孔孔径和间距分别为0.11m和3m．

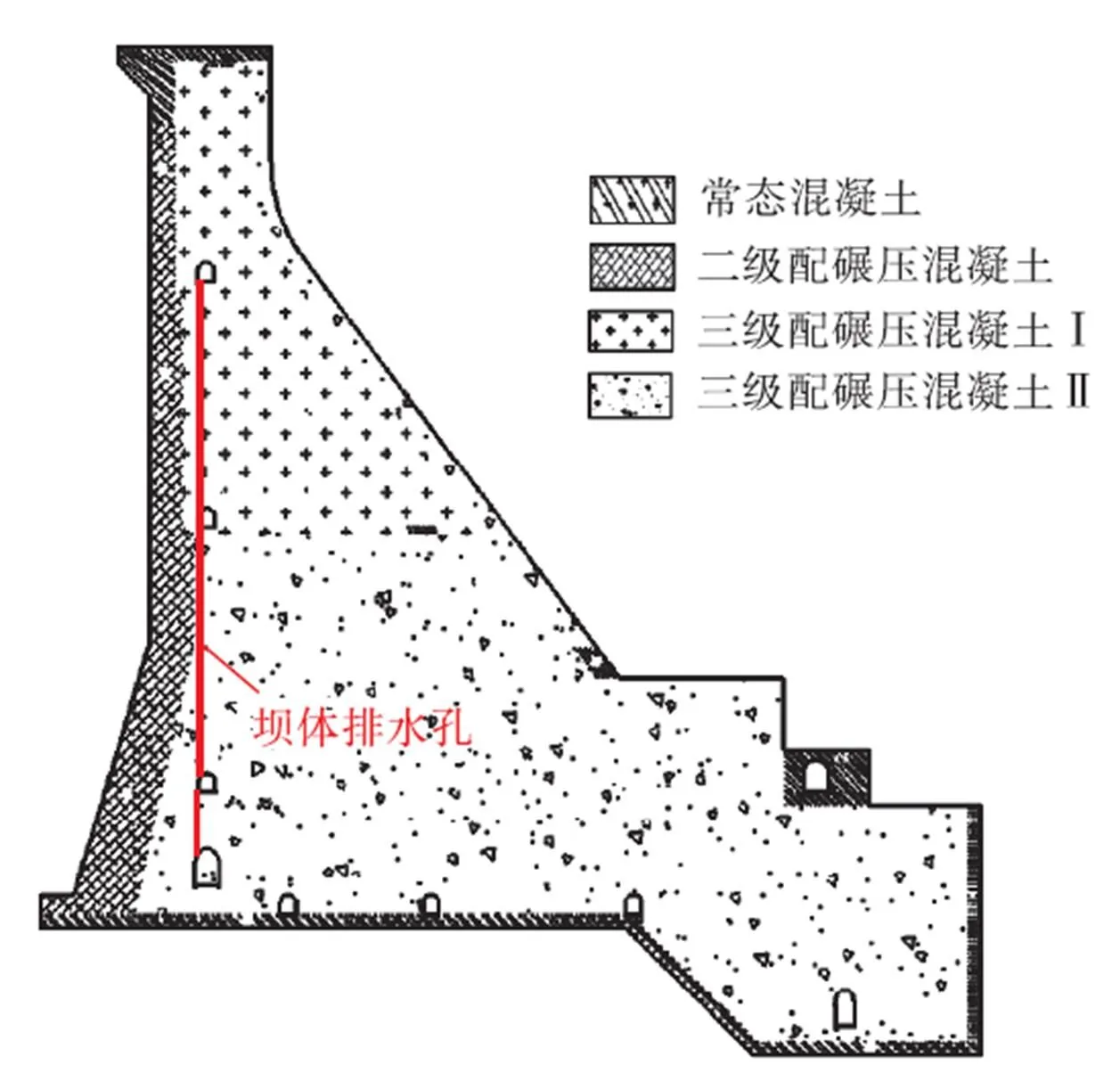
图4  渗控结构示意

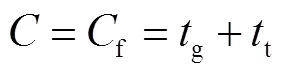
4.1  构建代理模型

表1  样本与对应的模拟结果

Tab.1 Samples and their corresponding simulation re-sults

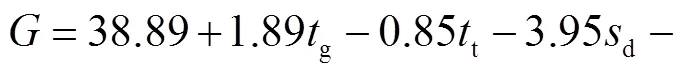
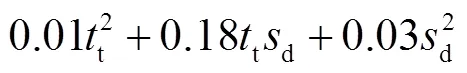
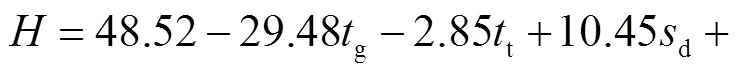
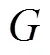
4.2  渗控结构多目标优化

将式(12)～式(14)代入到式(1)中，得到厂房坝段碾压混凝土坝坝体渗控结构多目标优化数学模型的具体表达式．然后，采用多目标粒子群算法对其进行求解，其中，种群大小设置为100，最大迭代代数设置为200．

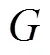
Tab.2  Comparison between the estimated and simulated values of and for the test samples

图5  Pareto解集散点分布

表3为从Pareto解集中选出的10组优化方案及对应的目标函数值．从表中可以看出，每一组粒子对应的目标函数值相比于优化之前的目标函数值整体上均得到了一定程度的优化，表明多目标粒子群优化算法能够获得具有多样性且质量较高的渗控结构设计方案，验证了基于代理模型的碾压混凝土坝坝体渗控结构多目标优化方法的有效性．

表3  优化方案及对应的目标函数值

Tab.3 Optimization schemes and their corresponding objective function values

利用已有的多种渗控结构设计方案比选研究成果、专家决策或者为满足特殊要求(如仅考虑安全性)，即可从表3中的10组优化方案中遴选出一组粒子作为渗控结构的最优设计方案．

本文采用TOPSIS法[31]对上述10组粒子进行比选．首先，对各组目标函数值进行向量规范化处理，得到对应的规范化指标；其次，根据各优化目标的重要性确定权重向量，这里采用的权重向量为[1/3，1/3，1/3]；再次，筛选出各优化目标的正理想解与负理想解；然后，分别计算各组粒子的规范化指标到正理想解和到负理想解的欧式距离；最后，计算各组粒子的规范化指标与理想解的相对接近程度，选取与正理想解相对接近度最高的粒子为决策解．根据以上步骤，得到各组粒子排序结果如表4所示．由表可知，7号粒子为排名第1的粒子，因此，选择7号粒子作为最终优选渗控结构设计方案．

表4  优化方案排序结果

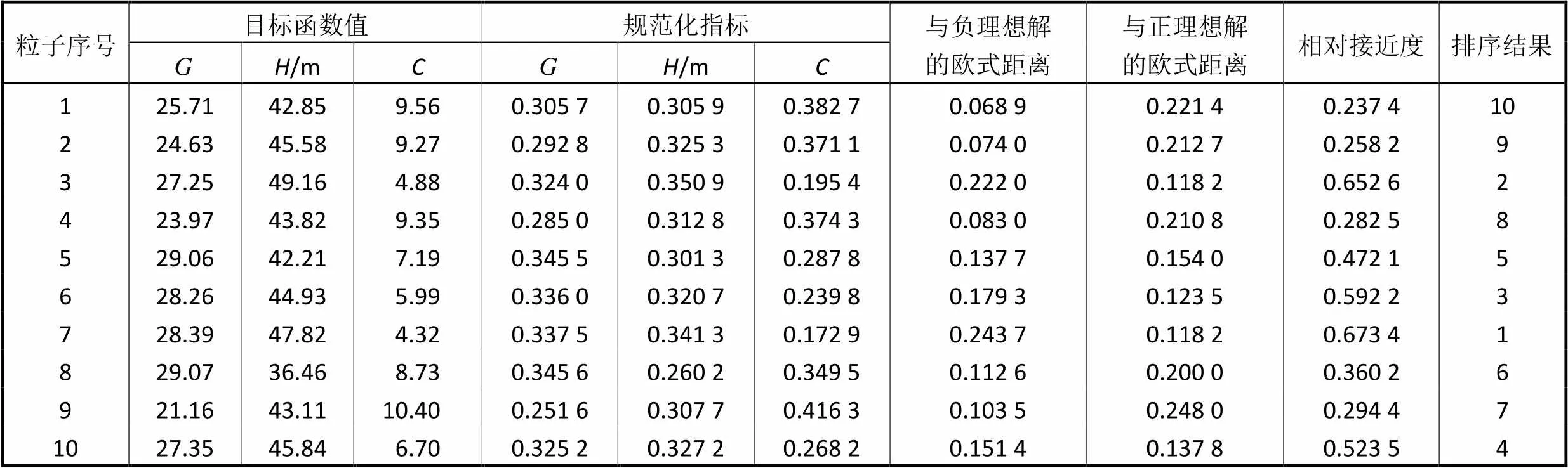
Tab.4  Ranking result of the optimization schemes

4.3  讨 论

上文采用本研究提出的方法对某碾压混凝土坝厂房坝段的坝体渗控结构进行多目标优化，获得了Pareto解集，并采用TOPSIS法对Pareto解集进行排序，从而得到最终优选渗控结构设计方案．

表5为7号粒子(最终优选渗控结构设计方案)与传统方法渗控结构优化结果的对比．从表中可以看出，7号粒子的坝体渗流量、防渗层最大水力梯度、渗控结构造价等指标均明显优于传统优化方法的结果，平均优化幅度达到10.18%；溢出点高程虽然上升了6.46%，但是尚在可接受范围之内．此外，由于本文方法通过代理模型实现对多个设计参数同时进行优化，避免了传统方法需要进行的多次数值模拟试验，使得计算耗时仅为传统方法的1/30．因此，结合坝体渗控结构的安全性和经济性两个目标来看，采用多目标粒子群算法得到的优选渗控结构设计方案相比于传统优化方法的结果整体上更加经济、更加合理，并且求解效率得到了大幅度提升，验证了基于代理模型的碾压混凝土坝坝体渗控结构多目标优化方法的优越性．

表5  7号粒子与传统方法渗控结构优化结果对比

Tab.5  Comparison between the No.7 particle and the optimization results of the traditional method

综上所述，由于本文是以防渗层最大水力梯度小、溢出点高程低和渗控结构造价低为目标对碾压混凝土坝坝体渗控结构进行多参数联合优化，避免了单目标、单参数的优化方法的盲目性，充分考虑了不同目标之间的冲突关系以及不同设计参数之间的关联性，所以在上述实例中，采用本文方法能够得到渗控效果更优、造价更低的渗控结构设计方案．

5  结 语

针对目前碾压混凝土坝坝体渗控结构优化研究中常用的单目标、单参数优化方法难以获得同时满足多个目标要求的渗控结构设计方案，无法充分考虑不同设计参数之间的关联性而且计算效率较低的不足，本文开展了基于代理模型的碾压混凝土坝坝体渗控结构多目标优化研究．首先，建立了以渗控结构设计参数为设计变量，以防渗层最大水力梯度、溢出点高程以及渗控结构造价为优化目标的碾压混凝土坝坝体渗控结构多目标优化数学模型；其次，构建渗控结构设计参数与优化目标之间的代理模型，用以替代优化过程中计算耗时的渗流数值模型，从而既提高了求解效率，又考虑了不同设计参数之间的关联性；然后，提出基于多目标粒子群算法与代理模型的模型求解方法，进而实现了对碾压混凝土坝坝体渗控结构的多目标优化．实例表明：本文方法能够快速地获取每个解均满足多个目标要求的Pareto解集，为获得优良的碾压混凝土坝坝体渗控结构设计方案提供支持；与传统优化方法相比，其渗控结构优化结果更为合理、有效．

［1］ 关新强. 特高碾压混凝土重力坝渗流特性及渗控措施研究[D]. 南京：河海大学水利水电工程学院，2007.

Guan Xinqiang. Study on Seepage Property and Methods for Control of Seepage in High RCC Gravity Dams[D]. Nanjing：College of Water Conservancy and Hydroelectric Engineering，Hohai University，2007(in Chinese).

［2］ 朱岳明，储小钊. 碾压混凝土坝防渗结构型式的工程实践[J]. 河海大学学报：自然科学版，2003，31(1)：16-20.

Zhu Yueming，Chu Xiaozhao. Practice in seepage prevention structures of roller-compacted concrete dams[J]. Journal of Hohai University：Natural Sciences，2003，31(1)：16-20(in Chinese).

［3］ 朱岳明，袁翠平，钱 敏，等. 碾压混凝土坝的渗流与控制(一)[J]. 红水河，2004，23(3)：1-4.

Zhu Yueming，Yuan Cuiping，Qian Min，et al. On seepage property and seepage control of RCC dam(1)[J]. Hongshui River，2004，23(3)：1-4(in Chinese).

［4］ 朱岳明，袁翠平，钱 敏，等. 碾压混凝土坝的渗流与控制(二)[J]. 红水河，2004，23(4)：4-8.

Zhu Yueming，Yuan Cuiping，Qian Min，et al. On seepage property and seepage control of RCC dam(2)[J]. Hongshui River，2004，23(4)：4-8(in Chinese).

［5］ 崔皓东，朱岳明. 200m 级RCC重力坝优选渗控设计方案研究[J]. 水利学报，2007：184-188.

Cui Haodong，Zhu Yueming. Study on reasonable seepage control scheme of 200m height RCC gravity dam[J]. Journal of Hydraulic Engineering，2007：184-188(in Chinese).

［6］ 黄 蓓，王育江，钱春香. 碾压混凝土坝防渗体设计的相关试验研究[J]. 水力发电，2010，36(10)：101-103.

Huang Bei，Wang Yujiang，Qian Chunxiang. Experinmental study on the impervious body design of roller compacted concrete dam[J]. Hydroelectric Power，2010，36(10)：101-103(in Chinese).

［7］ 李明超，王孜越，郭鑫宇，等. 碾压混凝土坝防渗层及渗控结构优化分析[J]. 应用力学学报，2016，33(6)：1064-1070.

Li Mingchao，Wang Ziyue，Guo Xinyu，et al. Seepage simulation and optimization for impervious structures of roller compacted concrete dam[J]. Chinese Journal of Applied Mechanics，2016，33(6)：1064-1070(in Chinese).

［8］ Li Mingchao，Zhang Mengxi，Hu Yu，et al. Mechanical properties investigation of high-fluidity impermeable and anti-cracking concrete in high roller-compacted concrete dams[J]. Construction and Building Materials，2017，156：861-870.

［9］ 黄宇容. 复杂地基渠道抗浮稳定及渗控优化研究[D]. 郑州：郑州大学水利与环境学院，2012.

Huang Yurong. Study on the Stability Against Floatation of Channel on Complex Ground and Optimization of Seepage Control[D]. Zhengzhou：School of Water Conservancy and Environment Engineering，Zhengzhou University，2012(in Chinese).

［10］ Li Xing，Chen Yifeng，Hu Ran，et al. Towards an optimization design of seepage control：A case study in dam engineering[J]. Science China Technological Sciences，2017，60(12)：1903-1916.

［11］ Tabari M M R，Mari M M. The integrated approach of simulation and optimization in determining the optimum dimensions of canal for seepage control[J]. Water Resources Management，2016，30(3)：1271-1292.

［12］ 宋晓猛，张建云，孔凡哲，等. 基于代理模型的水文模型参数多目标优化[J]. 四川大学学报：工程科学版，2014，46(2)：36-45.

Song Xiaomeng，Zhang Jianyun，Kong Fanzhe，et al. Multi-objective optimization for hydrological models using surrogate modeling[J]. Journal of Sichuan University：Engineering Science Edition，2014，46(2)：36-45(in Chinese).

［13］ 毕凤荣，刘建飞，姚昱儒，等. 基于Kriging模型的动力总成悬置系统多目标优化[J]. 天津大学学报：自然科学与工程技术版，2017，50(3)：328-334.

Bi Fengrong，Liu Jianfei，Yao Yuru，et al. Multi-objective optimization of powertrain mounting system based on Kriging model[J]. Journal of Tianjin University：Science and Technology，2017，50(3)：328-334(in Chinese).

［14］ 龙 腾，李学亮，黄 波，等. 基于自适应代理模型的翼型气动隐身多目标优化[J]. 机械工程学报，2016，52(22)：101-111.

Long Teng，Li Xueliang，Huang Bo，et al. Aerodynamic and stealthy performance optimization of airfoil based on adaptive surrogate model[J]. Journal of Mechanical Engineering，2016，52(22)：101-111(in Chinese).

［15］ 刘 颖，张 凯，于向军. 基于代理模型的中空轴式大型静压轴承多目标优化[J]. 吉林大学学报：工学版，2017，47(4)：1130-1137.

Liu Ying，Zhang Kai，Yu Xiangjun. Multi-objective optimization of hydrostatic bearing of hollow shaft based on surrogate model[J]. Journal of Jilin University：Engineering and Technology Edition，2017，47(4)：1130-1137(in Chinese).

［16］ 高轶男. 基于组合代理模型的汽车碰撞安全性多目标优化研究[D]. 重庆：重庆大学汽车工程学院，2016.

Gao Yinan. Multi Objective Optimization of Vehicle Crashworthiness Based on Surrogate Model[D]. Chongqing：College of Automobile Engineering，Chongqing University，2016(in Chinese).

［17］ 谷海涛，林 扬，胡志强，等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报，2009，45(12)：7-14.

Gu Haitao，Lin Yang，Hu Zhiqiang，et al. Surrogate models based optimization methods for the design of underwater glider wing[J]. Journal of Mechanical Engineering，2009，45(12)：7-14(in Chinese).

［18］ Razavi S，Tolson B A，Burn D H. Review of surrogate modeling in water resources[J]. Water Resources Research，2012，48(7)：W07401-1-32.

［19］ 柴军瑞，李守义，陈尧隆. 碾压混凝土重力坝防渗设施设计研究[J]. 西安理工大学学报，2000，16(3)：292-295.

Chai Junrui，Li Shouyi，Chen Yaolong. Optimal design of seepage control measures for rolled compacted concrete dam[J]. Journal of Xi’an University of Technology，2000，16(3)：292-295(in Chinese).

［20］ 刘恒丽，董靖川，于治强. 基于Pareto遗传算法和TRIZ理论的数控装备加工参数智能优化[J]. 天津大学学报：自然科学与工程技术版，2017，50(2)：121-127.

Liu Hengli，Dong Jingchuan，Yu Zhiqiang. Intelligent optimization of CNC equipment machining parameters based on pareto genetic algorithm and TRIZ theory[J]. Journal of Tianjin University：Science and Technology，2017，50(2)：121-127(in Chinese).

［21］ 何镓梁. 基于Kriging代理模型的多目标优化策略及其在PX氧化反应中的应用[D]. 上海：华东理工大学信息科学与工程学院，2012.

He Jialiang. A Multi-objective Optimization Strategy Based on Kriging Surrogate Model and Its Application in PX Oxidation Process[D]. Shanghai：College of Information Science and Engineering，East China University of Science and Technology，2012(in Chinese).

［22］ 赵 悦，练 冲，练继建，等. 海上风电筒型结构基础层状地基参数优化反演[J]. 天津大学学报：自然科学与工程技术版，2019，52(4)：423-429.

Zhao Yue，Lian Chong，Lian Jijian，et al. Optimization inversion of multi-layer subsoil parameters for offshore wind turbine structure supported by bucket foundation[J]. Journal of Tianjin University：Science and Technology，2019，52(4)：423-429(in Chinese).

［23］ Kennedy J，Eberhart R. Particle swarm optimization [C]//IEEE International Conference on Neural Networks. Perth，Australia，1995：1942-1948.

［24］ 叶礼裕，王 超，黄 胜，等. 基于多目标粒子群算法的螺旋桨多参数优化设计[J]. 武汉理工大学学报：交通科学与工程版，2015，39(6)：1169-1174.

Ye Liyu，Wang Chao，Huang Sheng，et al. Multi-parameters optimization design of ship propeller based on multi-objective particle swarm algorithm[J]. Journal of Wuhan University of Technology：Transportation Science and Engineering，2015，39(6)：1169-1174(in Chinese).

［25］ 张聪誉，陈民铀，罗辞勇，等. 基于多目标粒子群算法的电力系统无功优化[J]. 电力系统保护与控制，2010，38(20)：153-158.

Zhang Congyu，Chen Minyou，Luo Ciyong，et al. Power system reactive power optimization based on multi-objective particle swarm algorithm[J]. Power System Protection and Control，2010，38(20)：153-158(in Chinese).

［26］ 刘亚萌，蒋 劲，李 婷，等. 基于多目标粒子群算法的停泵水锤防护优化[J]. 中国农村水利水电，2017(6)：162-167.

Liu Yameng，Jiang Jin，Li Ting，et al. Optimization of water hammer protection based on multi-objective particle swarm algorithm[J]. China Rural Water and Hydropower，2017(6)：162-167(in Chinese).

［27］ 余建星，刘晓强，余 杨，等. 基于改进响应面法的立管疲劳可靠性计算[J]. 天津大学学报：自然科学与工程技术版，2017，50(10)：1011-1017.

Yu Jianxing，Liu Xiaoqiang，Yu Yang，et al. Calculation on fatigue reliability of riser based on improved response surface method[J]. Journal of Tianjin Univer-sity：Science and Technology，2017，50(10)：1011-1017(in Chinese).

［28］ 梁明轩，王晓林，袁惠群，等. 基于响应面法的轿车主减速齿轮可靠性灵敏度研究[J]. 中国机械工程，2016，27(4)：555-559.

Liang Mingxuan，Wang Xiaolin，Yuan Huiqun，et al. Reliability sensitivity for main reduction gears of a car based on response surface methods[J]. China Mechanical Engineering，2016，27(4)：555-559(in Chinese).

［29］ 程正飞，王晓玲，吕 鹏，等. 基于VOF法的碾压混凝土坝自由渗流场数值模拟[J]. 水利学报，2015，46(5)：558-566.

Cheng Zhengfei，Wang Xiaoling，Lü Peng，et al. Numerical simulation of free seepage field in RCC dams based on VOF method[J]. Journal of Hydraulic Engineering，2015，46(5)：558-566(in Chinese).

［30］ 中华人民共和国水利部. SL314—2004碾压混凝土坝设计规范[S]. 北京：中国电力出版社，2004.

The Ministry of Water Resources of the People’s Republic of China. SL314—2004 Roller Compacted Concrete Dam Design Specification[S]. Beijing：China Electric Power Press，2004(in Chinese).

［31］ 钟登华，程 普，任炳昱，等. 基于粒子群算法的高拱坝仓面排序多目标优化研究[J]. 水力发电学报，2015，34(8)：7-17.

Zhong Denghua，Cheng Pu，Ren Bingyu，et al. Study on multi-objective particle swarm optimization of concrete-placement sequencing for high arch dam[J]. Journal of Hydroelectric Engineering，2015，34(8)：7-17(in Chinese).

Multi-Objective Optimization of Seepage Control Structures of RCC Dams Based on the Surrogate Model

Cheng Zhengfei，Wang Xiaoling，Ren Bingyu，Lü Peng，Yu Hongling

(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

The single-objective and single-parameter optimization method is commonly used in the optimization of seepage control structures of roller-compacted concrete(RCC)dams，for which a seepage control structure design scheme that simultaneously satisfies multiple target requirements is difficult to obtain. Moreover，the method cannot fully consider the correlation between different designparameters，and its computational efficiency is low. In this study，a multi-objective optimization method based on the surrogate model was proposed for the seepage control structures of RCC dams. In the proposed method，①a mathematical model，which utilizes the design parameters of the seepage control structure as the design variables and the maximum hydraulic gradient of the impervious layers，overflow elevation，and seepage control structure cost as the optimization targets，was established for the multi-objective optimization of the seepage control structures of RCC dams and ②a model solution method based on the multi-objective particle swarm optimization(MOPSO)algorithm and the surrogate model，in which the MOPSO algorithm was applied to rapidly solve the Pareto solution set，was proposed. Moreover，the surrogate model was used to establish an approximate relationship between the design parameters and the optimization objectives to replace the time-consuming seepage numerical model in the optimization process. Thus，the solution efficiency was improved and the correlation between different design parameters was fully considered. The proposed method was applied to optimize the seepage control structure of a practical RCC dam，and its effectiveness and advantages were validated by comparing with traditional method.

RCC dam；seepage control structure；multi-objective optimization；surrogate model；MOPSO algorithm

TV642.2

A

0493-2137(2019)08-0793-11

10.11784/tdxbz201805069

2018-05-30；

2018-07-15.

程正飞（1988—  ），男，博士研究生，chengzf_tju@163.com.

王晓玲，wangxl@tju.edu.cn.

国家自然科学基金资助项目(51439005，51339003)；国家自然科学基金创新研究群体资助项目(51621092).

the National Natural Science Foundation of China(No.51439005，No.51339003)，the Science Fund for Creative Research Groups of the National Natural Science Foundation of China(No.51621092).

(责任编辑：王晓燕)