集中供热管网的非稳态水力建模与动态响应分析

由世俊，米雷洋，王雅然，张 欢，郑雪晶，郑万冬



集中供热管网的非稳态水力建模与动态响应分析

由世俊，米雷洋，王雅然，张 欢，郑雪晶，郑万冬

(天津大学环境科学与工程学院，天津 300350)

建立了单个供热管段的非稳态水力模型，导出了该非稳态水力模型的解析解，分析了管道长度、管径、进出口压差变化时管道流体的动态响应特性．当单个管道的进出口压差变化相同，管道的长度越长、管径越大时，管道的流量响应时间越慢；对于相同规格的管道，当管道的进出口压差变化越大时，管道流体的动态响应速度越快．在单个管段的非稳态水力模型的基础上，结合图论的方法建立了集中供热管网的非稳态水力模型，并构建了该模型的数值求解方法．该模型考虑管网运行调节时阀门开度或水泵转速改变等影响动态响应时间的因素，提出的非稳态水力模型和求解方法为热网进行频繁、大范围水力工况调节过程中各热力站流量的动态响应分析提供了支持．对一个实际热网的动态水力进行了分析，结果表明：当热网中的阀门开度不变、热源泵转速发生变化时，距离热源越远的热力站的流量动态响应时间越长；同样地，当热网中热源泵的转速不变、改变某一热力站的阀门开度时，距离热源越远的热力站的流量动态响应时间越长．

非稳态水力模型；图论；集中供热管网；动态响应时间；运行调节

集中供热管网的动态水力和热力特性对系统的运行调节至关重要．热网的动态热力特性主要体现在供热管道中热媒温度的传输延迟[1]，动态水力特性主要表现为阀门和水泵调节后，各个支路流量的动态响应．热网的稳态水力特性可以由节点流量平衡和回路压力平衡结合图论的方法来描述[2]，并且基于稳态水力模型数值计算的仿真和优化调度技术已经在集中供热系统的运行分析和调节中得到广泛而有效的应用[2]．

热网在运行过程中，热源需要通过调节热源泵的转速实现热源流量的调度，各个热力站则利用本地闭环控制系统通过改变一次侧阀门的开度实现流量的自动调节[3-4]．而阀门和水泵的动作会使热网中各个管段的流量经历一个动态过程，一方面，热网流量的动态响应时间将对热网的水力调节产生影响；另一方面，随着通信技术和自动化技术的发展，一些先进的通信技术和控制技术在不断地应用到热网当中，热网智能化趋势不可避免，为了在满足用户热舒适的前提下，最大限度地节省热网的输配能耗，依赖于精细化的供热调节，而热网流量的动态响应时间也是精细化供热调节时间间隔的依据．因此，建立管道和热网的非稳态水力模型，并分析管道和热网的动态响应特性具有重要的意义．

目前关于供热管网的非稳态水力特性的研究主要集中在供热管网的水锤问题及管网的慢变流问题．蔡启林等[5]建立了供热管网的水锤计算的数学模型，通过实例验证了该模型的正确性；还研究了供热系统水锤防护的措施，为供热管网的设计和运行提供了参考．曹慧哲等[6]基于图论建立了环状管网慢变流的水力计算模型，给出了管网慢变流模型的数值模拟方法；并基于慢变流理论提出了一种管网泄漏诊断与定位的模型，对管网阻抗的辨识和管网的故障诊断具有重要的参考价值．

本文从最基本的质量守恒和能量守恒原理出发，建立了单个管段和集中供热管网的动态水力模型，给出了一种新的集中供热管网慢变流建模和数值求解方法，为集中供热系统的动态水力特性分析提供补充．所建立的集中热网的动态水力模型既适用于规模不同的枝状管网，也适用于环状管网的水力特性分析．同时，本文推导出了管段流量的瞬态响应时间的计算公式，分析了不同管径、管长的管道的瞬态响应时间．最后，根据所建立的集中供热管网的动态水力模型，通过一个实例分析了热网运行过程中热源泵的转速变化和热力站阀门开度变化时热网的非稳态水力响应特性．

1 单个管段的非稳态水力特性

1.1 单个管段的非稳态水力建模

图1是单个管段流体非稳态流动的动量方程推导示意．坐标轴沿管道中心线方向，控制体的标高为，根据牛顿第二定律得到以下方程：

式中：为流体沿坐标轴的压力分布；为断面面积，m2；δ为控制体的厚度，m；0为管道壁面对控制体的切应力，Pa；为控制体的密度，kg/m3；为重力加速度，取9.8m/s2；为管道中心线与水平面的夹角；为控制体的加速度，m/s2．

图1  单个管段流体非稳态流动动量方程推导示意

消去δ，式(1)可以化简为[7]

在上述两式中，切应力0可以按照稳态工况下的达西公式计算：

式中：为沿程阻力损失系数；为断面平均流速，m/s；为管长，m；为管道直径，m．

在稳态工况下，对于长度为、管径为的水平管道，壁面切应力引起的阻力与按照达西公式计算得到的阻力相等且满足下式：

由此可以解得切应力0为

加速度可以分解成如下形式：

式中：v为速度对位置的偏导数；v为速度对时间的偏导数．

在上述分析当中，忽略压力波在管道中的传播和衰减过程，而且管道中的压力波的传播速度要远快于流量的动态变化速度；又由于供热管道中的热水近似为不可压缩流体，因此可将v近似为0．对于水平管段，＝0°；由于供热管段的坡度[8]一般为0.002～0.005，故对于有坡度的供热管段，sin≈0．根据以上条件，将式(5)和式(6)代入到式(2)中得

将上式从＝0到＝沿管长进行积分[9]，得

式中Δ＝0－L为管段的进出口压差，0为进口压力，L为出口压力．

式(8)的物理意义是：管段进出口压差Δ是使流体加速的动力，而管壁的黏性切应力则对流体起减速作用．当流体的运动状态达到稳态时，v＝0，方程(8)退化为描述管道稳态流动沿程阻力的达西公式．将式(8)中的流速改写成流量的形式，得到单个管段的非稳态水力模型表达式为

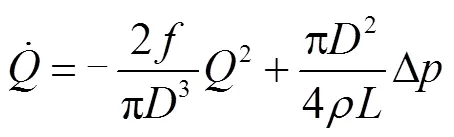
式(9)表示管段中流体流动的非稳态特性与管段的管径、长度、管段的阻力系数等有关．

1.2 单个管段非稳态水力建模的解析解

方程(9)描述了管道流体在非稳态流动过程中压力和流量变化之间的关系，它是1阶非线性常微分方程．设某管段在＝0时刻之前流体处于稳态，管段流体的流量为0，管段流体的进出口压差为Δ0．当＝0时刻时管段的进出口压差产生了一个阶跃，由Δ0变化为Δ1，此时刻之后管段的流量将经过一个瞬态的变化过程．

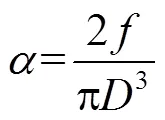
对式(10)两端进行积分，得

式(11)中，的表达式为

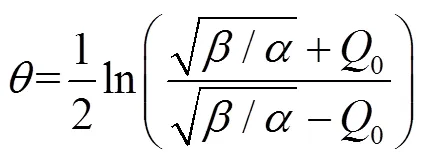
1.3 单个管段的非稳态水力特性分析

基于式(11)的关系对管道的非稳态水力特性进行分析，同时根据式(11)对管段内流体流动的响应速度进行研究，并探索管段内流体从静止过渡到另一个稳态时，管段流体流量的响应时间与管径、管长等管段物理参数之间的变化规律．

若管段初始状态的流量0＝0，则管段初始状态的进出口压差Δ0＝0．在＝0时刻，管段两端的压差从0阶跃为Δ1，由式(11)导出管段内流量随时间的变化规律如下：

达到稳态时的流量为

定义管段流量的瞬态响应时间r：管段初始状态的流量为0，当管段进出口压差从0阶跃为Δ1时，管段流量达到新的稳态流量(∞)的95%所需的时间r为管段流量的瞬态响应时间．根据式(14)和式(15)以及管段流量的瞬态响应时间的定义，可得

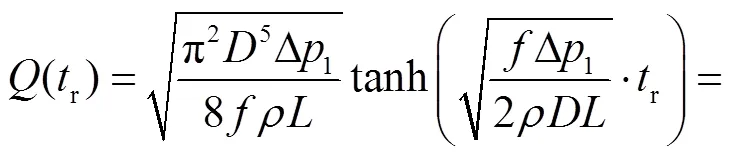
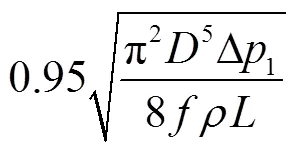
求解式(16)，得出管段流量的瞬态响应时间

由式(17)可以看出：管段的管径越大、长度越长，则管段流量的瞬态响应时间越长，流体从静止到新的稳态的过渡过程越缓慢；管段进出口压差越大，管段内流体达到稳态的时间越短．

图2所示为管径DN800、管长100m，管径DN800、管长200m和管径DN600、管长100m的3种不同规格的供热管段的瞬态响应时间．初始时刻，3根管道中的热水均处于静止状态，当3根管道的进出口压力差在＝0时刻阶跃为10kPa并保持恒定，3根管段的流量均经过一个暂态过程后达到稳定．由图2可以看出，管径为DN800、管长为100m的管段的瞬态响应时间为r＝55.6s，管径为DN800、管长为200m的管段的瞬态响应时间为r＝78.6s，管径为DN600、管长为100m的管段的瞬态响应时间为r＝46.4s．仿真结果表明：管段的长度越长，管径越大，管段的流量响应时间越慢．

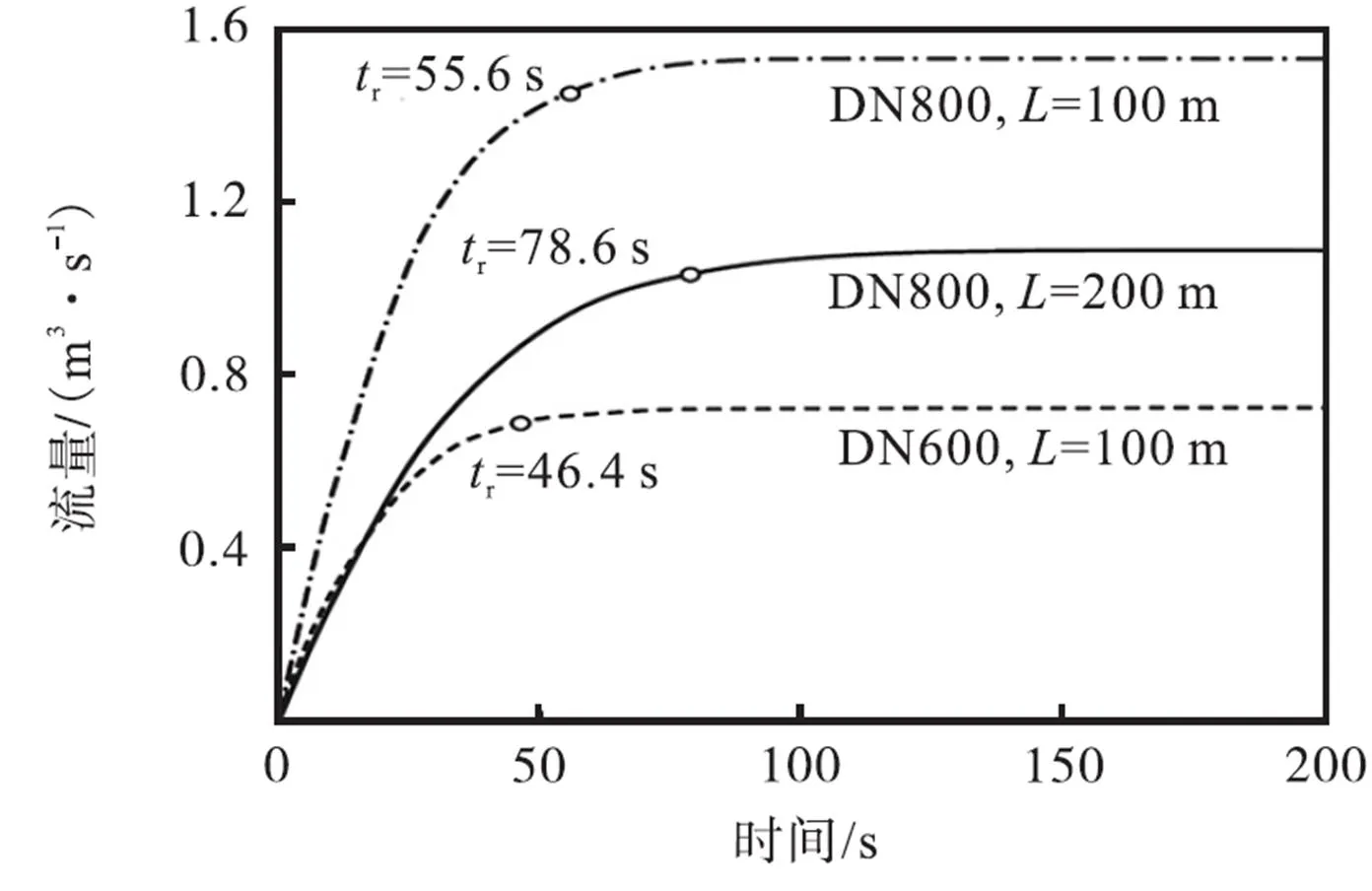
图2  不同管径、管长的管道流体动态响应过程

图3所示是相同管段在不同进出口压差变化情况下所引起的管段流体动态变化过程中的流量响应．可以看出，管径为DN800、长度为100m的供热管段，进出口压差从0Pa变为10kPa引起的瞬态流量响应时间为r＝55.6s，进出口压差从初态的0Pa变为20kPa引起的瞬态流量响应时间为r＝39.3s.表明进出口压差变化越大，动态响应速度越快．

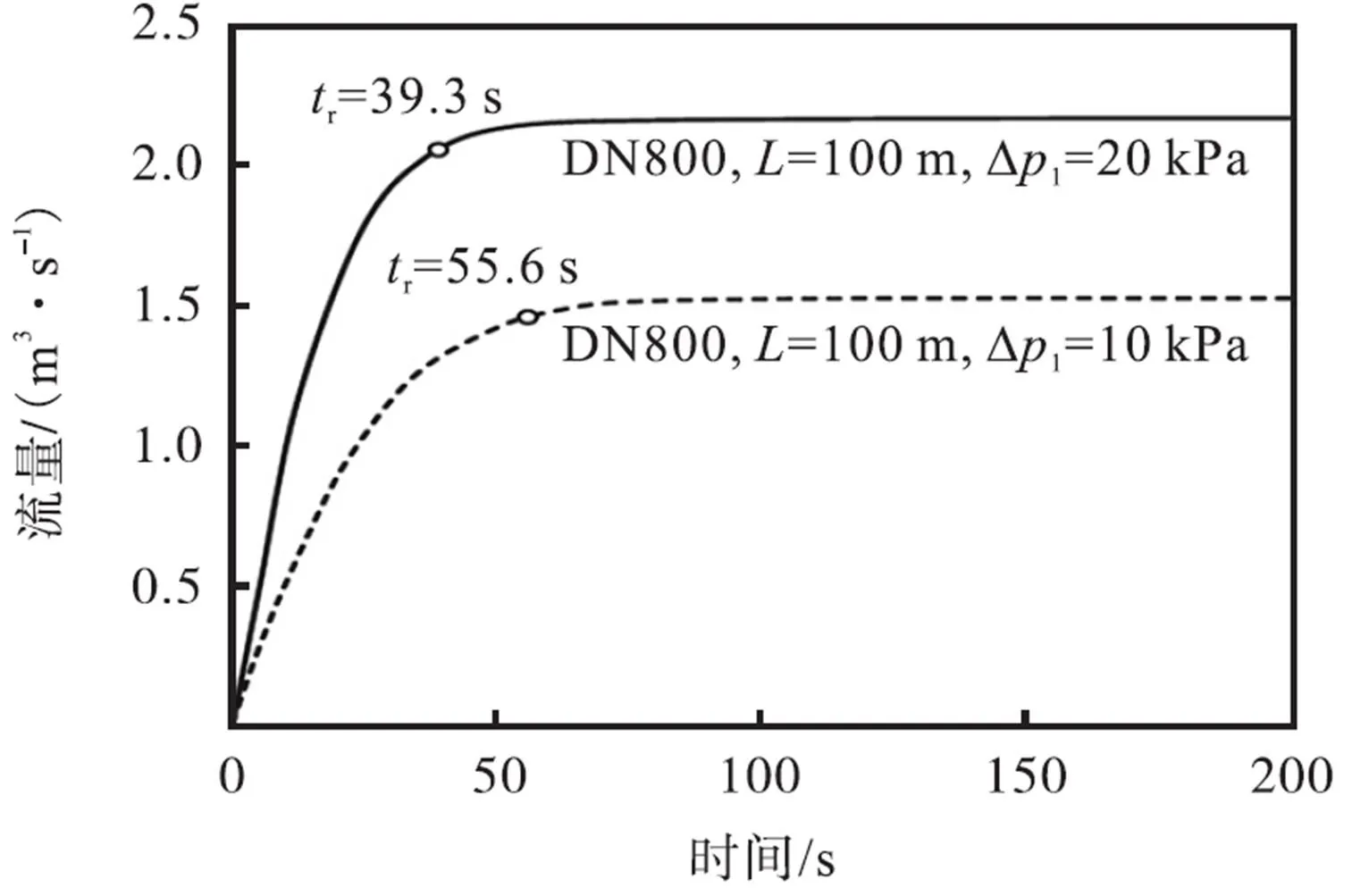
图3 不同进出口压差阶跃变化下的管道流体动态响应过程

图4所示是不同公称直径、不同长度管段中的热水由静止状态开始变化，在进出口压差从0Pa瞬间增加到10kPa时，各个管段中流体的瞬态响应时间．可以看出，不同规格管段流体的瞬态响应时间在几分钟到十几分钟之间变化．

图4  不同管径、不同管长的管道流体响应时间

2  集中供热管网的非稳态水力建模与分析

本文第1节给出了单个管段的非稳态水力特性描述，并得出了单个供热管段由一个稳态向另一个稳态过渡时的瞬态过程的解析解，即式(11)．但是当管网中有阀门的开度变化或者水泵转速的变化时，式(11)就不适用于分析管网的非稳态水力响应了．在考虑上述两个因素对管网的非稳态水力响应的影响时，必须联立各个管段的非稳态水力方程，即式(9).本节将建立集中供热管网的非稳态水力模型，并给出数值求解方法，进而分析管网的非稳态水力响应．

2.1 集中供热管网的非稳态水力模型的建立

与供热管网的稳态水力模型类似，集中供热管网的非稳态水力模型也可以采用图论的方法描述．由于热水在热网中的非稳态水力过程中是不可压缩的，故节点流量平衡方程和回路压力平衡方程[10]逐时地成立，满足以下两个方程式：

式中：k为管网的基本关联矩阵；f为管网的独立回路矩阵[10]；()为各个分支在时刻的流量向量；Δ()为各个分支在时刻的压差向量．

根据热网的节点流量平衡方程和回路压力平衡方程以及水泵扬程的特性方程p,i(n，Q)，管道的非稳态水力特性方程(9)可以写成如下形式：

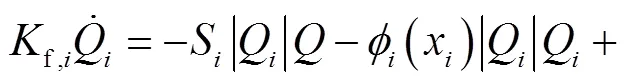
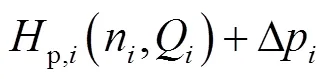
式中：Δp为各个管段的进出口压差；S为与局部阻力损失和沿程阻力损失相关的管路阻抗，即

f,i的表达式为

阀门开度变化与阀门阻抗(x)之间的关系可以通过下式表示：

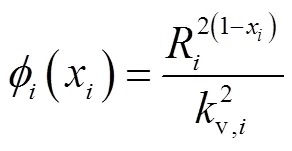
式中：(x)为等百分比阀门的阻抗，x为等百分比阀门的开度；R为阀门的可调比；v,i为阀门的流通能力.

若集中供热管网中有个管段，则个管段的动态水力特性方程可写成向量形式，即

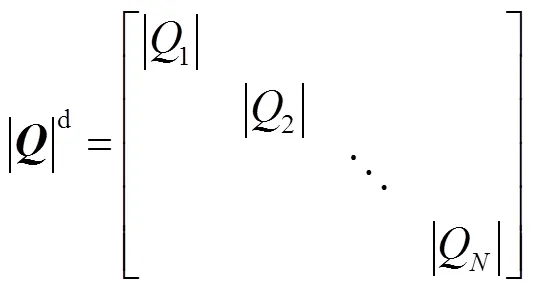
联立式(19)和式(24)，消掉Δ，得

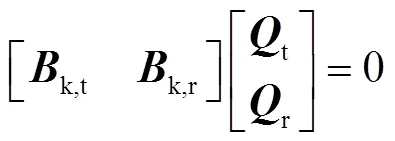
整个管网各个分支的流量向量也可以由余枝流量表示为如下形式：

其中

式中r是与余枝数阶数相等的单位矩阵．

将式(32)与式(33)代入式(29)中，得到整个管网的非稳态水力模型

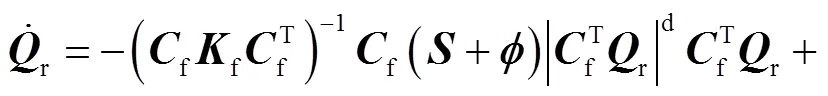
上述各式中未注释项代表的意义见上节．

式(34)是非线性常微分方程，该式中方程的数目与管网中的余枝数相等，即在节点数为、分支数为的管网中，余枝数为＋1．通过求解式(34)可以得到余枝流量随时间的变化，再根据式(31)可以得到树枝流量随时间的变化．

2.2 管网非稳态水力模型求解方法

由于集中供热管网的非稳态水力方程是非线性常微分方程组，直接获得其解析解很困难．为方便进行供热管网非稳态水力响应的分析，本文利用4阶Runge-Kutta法构造式(34)的数值求解格式[11]．设供热管网的初始状态下，余枝流量为r,0．设时间步长为Δ，第步的余枝流量为r,k，则第＋1步的余枝流量r,k＋1可由下式给出：

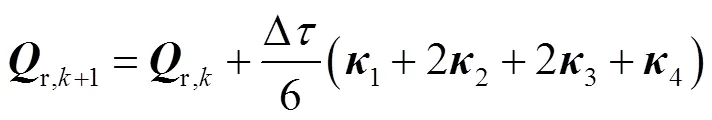
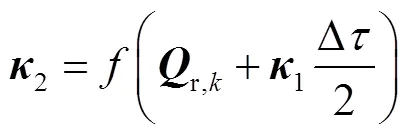
并且，

3 集中供热管网的非稳态水力分析

3.1 水泵转速变化对热网流量水力响应时间的影响

图5所示是某城镇的集中供热管网，该热网有一个环、两个热源和28个热力站，是典型的多热源环状热网，总供热负荷为190MW．热源1是热电厂，承担基本负荷，其供热能力为150MW．热源2是燃气调峰锅炉房，承担峰值负荷，其供热能力为55MW．在低负荷时，热源1承担全部热力站的负荷，热源1循环泵的调节会对各个热力站的流量产生影响，在分析热网各部分流量随着热源泵转速变化的响应特性时，考虑如下典型的情形：当热源1的水泵电机频率在1min内从50Hz线性地减为25Hz，而各个热力站的阀门开度保持不变时，分析各热力站的流量随时间的变化情况．本节将基于热网非稳态水力建模及求解方法，分析上述情形下各热力站的流量随时间的变化情况．

在MATLAB中编制上节所提出的基于4阶Runge-Kutta法的热网非稳态水力特性计算程序，并导入图5所示热网对应式(34)形式的非稳态水力模型，可以实现该热网动态水力工况的仿真计算．

图5  某城镇集中供热管网

在进行热网的非稳态水力模型求解时，为保证Runge-Kutta算法计算的数值稳定性，时间步长Δ不能选得过大，本例选取Δ＝0.1s，数值计算的总时长为30min．热源1处的循环水泵电机频率在＝0～5min内维持在50Hz不变，从＝5min开始，到＝6min时，热源1处循环水泵电机的频率从50Hz线性地减为25Hz，并从＝6min开始、到＝30min时，维持热源1处循环水泵电机的频率在25Hz不变，在整个过程中，各个热力站的阀门开度均维持在100%不变．部分热力站的流量随时间变化的计算结果见图6．

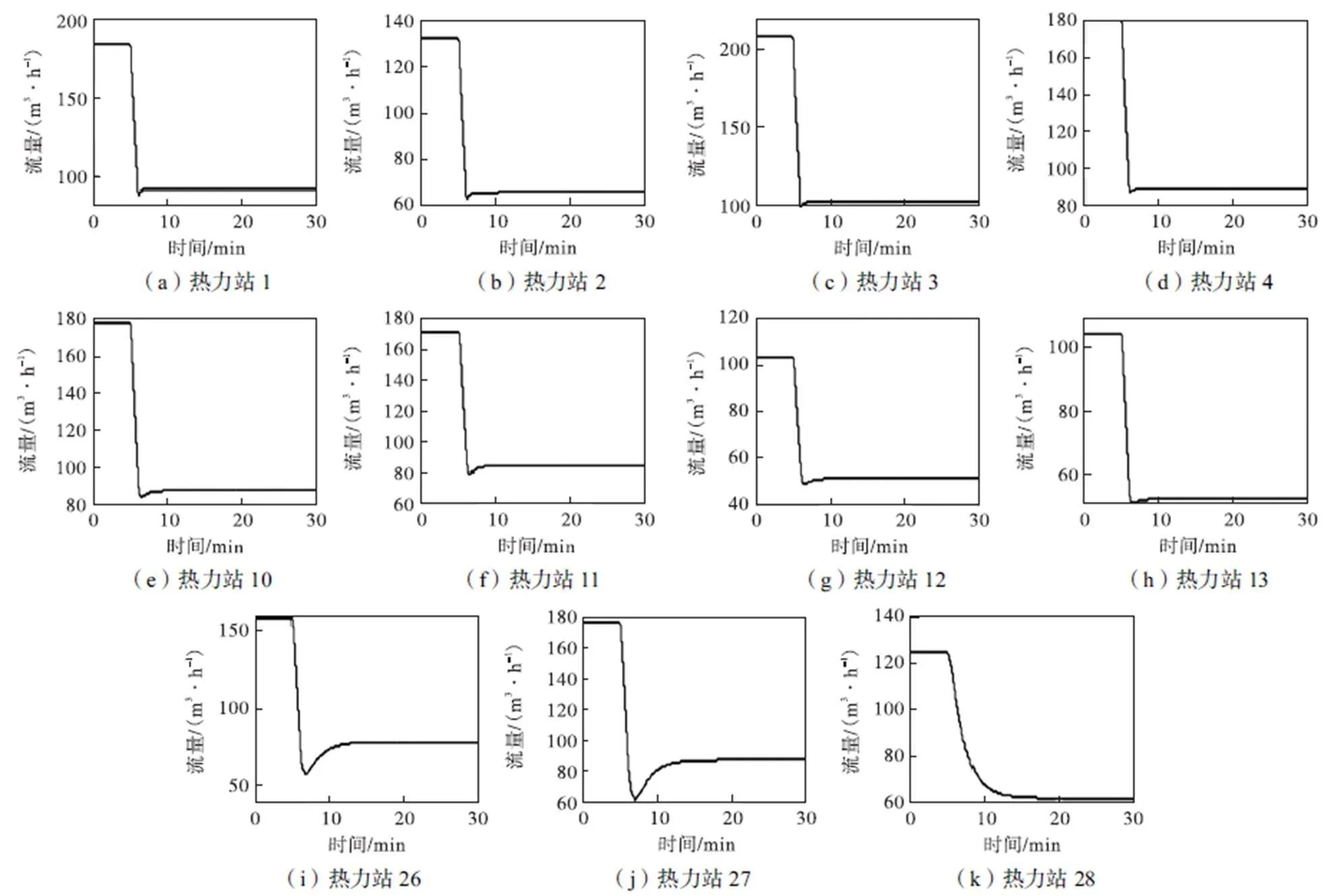
图6  热源泵调节时部分热力站的流量响应

从图6可以看出，当热源1的循环泵转速降低以后，热力站的流量经过一个瞬态过程，达到新的稳态值，且新的稳态值较热源1循环泵转速变化之前有所减少．从图6还可以得出，按管路距离计算，离热源1近的热力站流量的响应速度都比较快，例如1～4号热力站，其流量都在1min左右达到新的稳态值，见图6(a)～(d)．但随着与热源1管路距离的增大，热力站的流量响应速度逐渐变慢，例如10～13号热力站，其流量的响应时间在3～4min，见图6(e)～(h)．对于距离热源1较远的热力站，如26～28号热力站，其流量的响应时间在5～8min，见图6(i)～(k)．

3.2 阀门开度变化对热网流量水力响应时间的影响

对于热力站阀门开度变化下的各热力站流量响应特性，考虑令热源1的水泵电机频率保持50Hz不变，热力站1的阀门开度在1min内由100%线性地变化为50%．数值计算的总时长也为30min．热源1的循环水泵电机频率在＝0～30min内维持在50Hz不变．热力站1的阀门开度在＝0～5min内保持在100%不变，从＝5min开始、到＝6min时，热力站1的阀门开度从100%线性地变为50%，并从＝6min时开始、到＝30min时，维持热力站1的阀门开度在50%不变．在整个过程中，其余热力站的阀门开度均维持在100%不变．部分热力站的流量随时间变化的计算结果见图7．

从图7可以看出，当热力站1的阀门开度减小以后，其余热力站的流量都经过一个瞬态过程，达到新的稳态值，且新的稳态值较热力站1阀门动作之前都有所增加．同样地，从图7中也可以得出，按管路距离计算，离热力站1近的热力站流量响应速度都比较快，例如2～5号热力站，其流量都在1min内达到新的稳态值，见图7(a)～(d)．但随着与热源1管路距离的增大，热力站的流量响应速度逐渐变慢，例如9～13号热力站，其流量的响应时间在2min左右，见图7(e)～(i)．对于距离热源1较远的热力站，如26～28号热力站，其流量的响应时间在4～6min左右，见图7(j)～图7(l)．

图7  阀门调节时部分热力站的流量响应

图7给出的结果表明：若热网中的阀门不动，热源泵转速发生变化以后，按管路距离计算，距离该热源越远的热力站，其流量的动态响应时间越长，反之则越短．同样地，若热网中的水泵不调节，而某一热力站的阀门开度发生变化后，按管路距离计算，距离阀门动作位置越远的热力站，其流量的动态响应时间越长，反之则越短．当热源循环泵的转速进行大范围调整时，各热力站的流量响应时间比热力站进行阀门调节所引起的流量响应时间长．

这些规律可以为大型热网的水力工况调节提供指导，并且，本文给出的建模与数值求解方法也为热网动态水力特性的量化分析和精细化调节提供支持.

4 结 论

(1) 本文建立的单个管段的非稳态水力模型可以用来计算分析单个不同规格管段的瞬态响应时间．利用该模型还可以得到单个管段的瞬态水力特性：管道的管径越大、长度越长，则管道两端压差发生变化后，流量的动态响应时间越长，流体从静止到新的稳态的过渡过程越缓慢；而若管道进出口压差变化越大，则管道流量的动态响应时间越短，流量达到新稳态的过程越快．

(2) 本文建立的集中供热管网的非稳态水力模型可以用来计算分析不同规模热网在水泵转速变化和阀门开度变化时各个热力站的动态响应时间及管网的动态水力特性．

(3) 算例中热源循环泵转速的变化和热力站阀门开度的变化过程所引起的动态水力响应的时间尺度在10min以内．对于更大规模的城市级的集中供热管网，动态水力响应时间会更长．为了保证供热管网的水力稳定性同时最大限度节省供热管网的输配能耗，当进行管网的运行调节时，可将本文所建立的管网非稳态水力模型和分析方法应用到热网中，根据计算出的动态响应时间作为制定水力工况调节时间间隔的依据．

［1］ Wang Yaran，You Shijun，Zhang Huan，et al. Thermal transient prediction of district heating pipeline：Optimal selection of the time and spatial steps for fast and accurate calculation[J]. Applied Energy，2017，206：900-910.

［2］ Wang Yaran，You Shijun，Zhang Huan，et al. Hydraulic performance optimization of meshed district heating network with multiple heat sources[J]. Energy，2017，126：603-621.

［3］ Wang Yaran，You Shijun，Zheng Wandong，et al. State space model and robust control of plate heat exchanger for dynamic performance improvement[J]. Applied Thermal Engineering，2018，158：1588-1604.

［4］ Wang Yaran，You Shijun，Zhang Huan，et al. Operation stability analysis of district heating substation from the control perspective[J]. Energy and Buildings，2017，154：373-390.

［5］ 蔡启林，李 锐. 热水供热网水锤计算数学模型[J]. 区域供热，1995(5)：28-32.

Cai Qilin，Li Rui. Mathematical model of water hammer in hot water heating network[J]. District Heating，1995(5)：28-32(in Chinese).

［6］ 曹慧哲，贺志宏，何钟怡. 基于图论的环状管网慢变流的计算研究[J]. 哈尔滨工业大学学报，2007，39(10)：1559-1563.

Cao Huizhe，He Zhihong，He Zhongyi. Analysis and calculation of the slow transient flow in the multi-loops network based on graph theory[J]. Journal of Harbin Institute of Technology，2007，39(10)：1559-1563(in Chinese).

［7］ Wylie E B，Streeter V L. Fluid Transients[M]. Osborne：McGraw-Hill，1978.

［8］ 贺 平，孙 刚，王 飞，等. 供热工程[M]. 4版. 北京：中国建筑工业出版社，2009.

He Ping，Sun Gang，Wang Fei，et al. Heating Engineering[M]. 4th ed. Beijing：China Architecture and Building Press，2009(in Chinese).

［9］ American Society of Heating，Refrigerating and Air Conditioning Engineers. ASHRAE Handbook of Fundamentals[M]. American：ASHRAE Handbook Committee，2013.

［10］ 付祥钊，肖益民. 流体输配管网[M]. 3版. 北京：中国建筑工业出版社，2010.

Fu Xiangzhao，Xiao Yimin. Fluid Supply Pipework[M]. 3rd ed. Beijing：China Architecture and Building Press，2010(in Chinese).

［11］ 李荣华，刘 播. 微分方程数值解法[M]. 3版. 北京：高等教育出版社，2009.

Li Ronghua，Liu Bo. Numerical Methods for Solution of Differential Equations[M]. 3rd ed. Beijing：Higher Education Press，2009(in Chinese).

Unsteady Hydraulic Modeling and Dynamic Response Analysis of a District Heating Network

You Shijun，Mi Leiyang，Wang Yaran，Zhang Huan，Zheng Xuejing，Zheng Wandong

(School of Environmental Science and Engineering，Tianjin University，Tianjin 300350，China)

In this paper，the unsteady hydraulic model of a single pipeline is established，and the analytical solution of the unsteady hydraulic model is derived．The dynamic response characteristics of the pipeline fluid are analyzed when the pipeline length，pipeline diameter and differential pressure of the inlet and outlet vary．When the differential pressure between the inlet and outlet of a single pipeline changes in the same way，the longer the length of the pipeline and the larger the diameter of the pipeline，the slower the flow response time of the pipeline；moreover，for the same size of the pipeline，the greater the differential pressure between the inlet and outlet of the pipeline，the higher the dynamic response speed of the fluid in the pipeline．Based on the dynamic model of a single pipe and graph theory，the dynamic hydraulic model of the whole district heating network is established，and the numerical solution method of the model is constructed．The model considers the factors affecting the dynamic response time，such as the opening of the valve or the rotational speed change of the pump，when the pipe network operation is adjusted．The proposed unsteady hydraulic model and solution method provide support for dynamic response analysis of the flow of each thermal station in the process of frequent and large-scale hydraulic regulation of the heat network．Through the dynamic hydraulic analysis of a practical heat network，it is determined that when the opening of the valve in the district heating network is constant and the speed of the heat source pump changes，the dynamic response time of the flow rate in the heating substation increases，if the distance of the heating substation away from the heat source increases．Similarly，when the speed of the heat source pump is constant and the valve opening of a heating substation is changed，the dynamic response time of the flow rate in the heating substation increases，if the distance of the heating substation away from the heat source increases．

unsteady hydraulic model；graph theory；district heating network；dynamic response time；operating regulation

TU995.3

A

0493-2137(2019)08-0849-08

10.11784/tdxbz201808091

2018-08-31；

2019-01-09.

由世俊（1955—  ），男，博士，教授，yousj@tju.edu.cn.

王雅然，wangyaran19900101@126.com.

(责任编辑：田 军)