满足某些条件的有限单群的分类

2019-06-11王玲丽张良才

中北大学学报(自然科学版) 2019年4期

王玲丽, 张良才

(1. 中北大学理学院，山西太原 030051； 2. 重庆大学数学与统计学院，重庆 401331)

0 引言

满足某些条件的有限群的分类问题是研究有限群论的重要课题之一，利用图研究有限群的性质是目前国内外群论学者的研究热点之一. 对于群G, 用πe(G)表示群G的元素的阶的集合, 用π(n)表示n的素因子的集合, 其中n是自然数，用π(G)表示|G|的素因子的集合.

与πe(G)有关的图称为G的素图Γ(G). 定义如下: 顶点集合是π(G), 如果pq∈πe(G)，两个点p,q相连，记为p～q[1]. 用t(G)表示Γ(G) 的连通分支数, 用πi=πi(G)(i=1,2,…,t(G))表示Γ(G)的连通分支. 当|G|是偶数时, 记2∈π1(G). 设p∈π(G), 在Γ(G)中, 与顶点p相连的边数称为p的度数，记为dG(p). 本文所涉及的群均指有限群, 单群均指有限非交换单群, 所用到的其他概念是标准的，可参见文献[2-3].

近年来，国内外群论学者大量研究了利用素图研究有限群方面的问题. Lucido等[4-5]研究了素图是树的群的分类，以及素图分支是完全图的群的分类. 2005年，Moghaddamfar等[6]研究了用素图的顶点度数刻画有限单群. Vasil’ev等[7-8]研究了素图性质与有限群结构之间的关系，有限单群的素图的连接标准，这些结论为研究素图连通的有限单群开辟了新的方法. 同时Vasll’ev等[9]在2011年给出了有限单群的素图的极大长度的团数. 2013年，Zvedina[10]给出了与交错群的素图相同的有限非交换单群. 这部分研究大都是利用素图性质研究有限非交换单群. 近年来，群论学者也利用素图性质研究有限群. 2013年，Zinovéva等[11]研究了素图非连通的有限群，Zavarnitsine[12]研究了素图含有一个5-分支的有限群. 2015年，Alexander[13]给出了可解群的素图刻画. 2017年，郝才攀[14]给出了5个顶点的有限群的素图分类. 2017年，包奕等[15]给出了某些具有完全素图的有限单群的分类.

综上所述，对于借助素图性质研究有限群方面的问题，主要集中在两方面，一是刻画问题，二是分类问题. 本文考虑了满足某些条件的有限非交换单群的分类，得到了7∈π(G),dG(7)=1且|G|<1010, 且素图每个分支都是完全图的有限单群的分类.

以下给出本文用到的重要结论.

引理1[5]令G是有限非交换单群, 则G的素图每个分支是完全图当且仅当G为下列群之一：

1) 交错群A5,A6,A7,A9,A12,A13.

2) 李型单群A1(q)(q>2),2B2(q)(q=22m+1),A2(4),2A2(9),C3(2),2A3(3),2A5(2),3D4(2),D4(2),C2(q),G2(3k),A2(q)(q是Mersenne素数),2A2(q)(q是Fermat素数).

3) 散在单群M11,M22,J1,J2,J3,HS.

为了讨论方便，给出如下和数论有关的结论.

引理21) 令r是个位数为9的素数，则5|(2·r·7-1)且 2·r·7-1≠5k.

2) 令r是个位数为1的素数，则5|(2·r·7+1)且 2·r·7+1≠5k.

证明1) 当r是个位数为9的素数时, 2·r·7-1 的个位数是5. 因此5|(2·r·7-1). 又因为5的方幂后两位数(十位和个位数)一定是25. 而2·r·7乘积的后两位数的值完全由r的后两位决定. 通过计算*9(其中*=1,2,…，9)与14的乘积, 可以得到*9·14后两位除了*9=59外都不是25. 而2·59·7-1=825不是5的方幂.

2) 同上述方法，可以类似得到结论.

1 主要结论

定理1设G是一个有限非交换单群, 满足

1)G的素图分支均为完全图，

2) 7∈π(G)且dG(7)=1，

3) |G|≤1010，

则G为下列群之一：A1(449),A1(113),A1(29),A1(197),A1(1 373),A1(41),A1(181),A1(433),A1(601),A1(853),A1(937),A1(1 021),A1(1 777),A1(2 113),A1(53),A1(349),A1(1 693),A1(293),A1(881),A1(223),A1(27),A1(1 567),A1(43),A1(71),A1(239),A1(659),A1(743),A1(827),A1(1 163),A1(1 499),A1(1 583),A1(2 087),A1(127),A1(379),A1(491),A1(883),A1(26),A1(29),2A2(17).

证明按上述引理1中的三部分进行分类讨论.

Ⅰ. 若G为交错群A5,A6,A7,A9,A12,A13.

由于 7∈π(G)且dG(7)= 1,G不可能是A5,A6,A7,A9. 当G=An,n≥12时, 设x=(1,2,3,4,5,6,7)(8,9)(10,11),y=(1,2,3,4,5,6,7)(8,9,10,11,12), 则x,y∈G, 且|x|=14, |y|=35. 从而有2～7, 5～7. 所以，dG(7)≥2.

故G不是交错群.

Ⅱ. 若G为李型单群A1(q)(q>2),2B2(q)(q=22m+1),A2(4),2A2(9),C3(2),2A3(3),2A5(2),3D4(2),D4(2),C2(q),G2(3k),A2(q)(q是Mersenne素数),2A2(q)(q是Fermat素数).

下面分别进行讨论：

1) 若G为李型单群A1(q)(q>2).

|A1(q)|=q(q2-1). 对于q分q≡1(mod 4),q≡-1(mod 4)及q≡0(mod 2)三种情况讨论.

a.q≡1(mod 4)

由文献[1]知,π1=π(q-1),π2=π(q),π3=π((q+1)/2). 由于7∈π(G)且dG(7)= 1, 有7∈π1或7∈π3两种情况.

情况17∈π1, 即q-1=2t·7s. 令q=2t·7s+1=4k+1. 由于|A1(q)|=q(q2-1)≤1010, 有1≤s<4,t≥2.

当s=1时,t<8. 当s=1,t=7时,q=27·7+1=897=3·299，不是素数幂. 当s=1,t=6时,q=26·7+1=449，是素数. 此时|A1(q)|=q(q2-1)=90 518 400=27·32·52·7·449<1010. 当s=1,t=5时,q=25·7+1=225=32·52不是素数幂. 当s=1,t=4时,q=24·7+1=113，是素数. 此时|A1(q)|=q(q2-1)=1 442 784=25·3·7·19·113<1010. 当s=1,t=3 时,q=23·7+1=57=3·19不是素数. 当s=1,t=2时,q=22·7+1=29是素数. 此时|A1(q)|=q(q2-1)=7 645 176=25·3·7·19·113<1010.

当s=2时,t<6. 当s=2,t=5时,q=25·72+1=1 569=3·523，不是素数幂. 当s=2,t=4时,q=24·72+1=785=5·157，不是素数幂. 当s=2,t=3时,q=23·72+1=393=3·131，不是素数幂. 当s=2,t=2时,q=22·72+1=197，是素数. 此时|A1(q)|=q(q2-1)=24 360=23·32·72·11·197<1010.

当s=3时,t=2.q=22·73+1=1 373，是素数. 此时|A1(q)|=q(q2-1)=2 588 280 744=23·3·73·229·1 373<1010.

情况27∈π3, 由于dG(7)= 1, 则|π(π3)|=2. 设(q+1)/2=rt·7s, 其中r≠2, 7，则q=2·rt·7s-1. 由于|A1(q)|=q(q2-1)<(q+1)3=23·r3t·73s≤1010, 有s=1,t=1时,r<153; 不超过153的素数有r=3,5,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151.s=1,t=2时,r<12, 即r=3,5,11；s=1,t=3时,r=3;s=2,t=1时,r<10, 即r=3,5；s=2,t=2时,r=3.

下面分别进行计算：

令s=1,t=1. 由引理2中1得, 当r=19,29,59,79,89,109,139,149时,q=2·r·7-1，不是素数幂.

当r=3时,q=2·3·7-1=41, 此时|A1(q)|=q(q2-1)=68 880=24·3·5·7·41<1010.r=5时,q=2·5·7-1=69, 不是素数幂.r=11时,q=2·11·7-1=153, 不是素数幂.r=13时,q=2·13·7-1=181, 此时|A1(q)|=q(q2-1)=5 929 560=23·32·5·7·13 ·181<1010.r=17时,q=2·17·7-1=237, 不是素数幂.r=23时,q=2·23·7-1=321, 不是素数幂.r=31时,q=2·31·7-1=433, 此时|A1(q)|=q(q2-1)=81 182 304=25·33·7·31 ·433<1010.r=37时,q=2·37·7-1=517=11·47, 不是素数幂.r=41时,q=2·41·7-1=573=3·191, 不是素数幂.r=43时,q=2·43·7-1=601, 此时|A1(q)|=q(q2-1)=217 081 200=24·3·55·7·43 ·601<1010.r=47时,q=2·47·7-1=657=32·73, 不是素数幂.r=53时,q=2·53·7-1=741=32·13·19, 不是素数幂.r=61时,q=2·61·7-1=853, 此时|A1(q)|=q(q2-1)=620 649 624=23·3·55·7·61·71 ·853<1010.r=67时,q=2·67·7-1=937, 此时|A1(q)|=q(q2-1)=822 656 016=24·32·7 ·13·67·937<1010.r=71时,q=2·71·7-1=993, 不是素数幂.r=73时,q=2·73·7-1=1 021, 此时|A1(q)|=q(q2-1)=1 064 331 240=23·3·5 ·7·17·73·1 021<1010.r=83时,q=2·83·7-1=1 161=33·43, 不是素数幂.r=97时,q=2·97·7-1=1 357=23·59, 不是素数幂.r=101时,q=2·101·7-1=1 413=32·157, 不是素数幂.r=103时,q=2·103·7-1=1 441=11·131, 不是素数幂.r=107时,q=2·107·7-1=1 497=3·499, 不是素数幂.r=113时,q=2·113·7-1=1 581=3·527, 不是素数幂.r=127时,q=2·127·7-1=1 777, 此时|A1(q)|=q(q2-1)=5 611 282 656=25·3 ·7·37·127·1 777<1010.r=131时,q=2·131·7-1=3·611, 不是素数幂.r=137时,q=2·137·7-1=1 917=33·71, 不是素数幂.r=151时,q=2·151·7-1=2 113, 此时|A1(q)|=q(q2-1)=9 434 054 784=27·3 ·7·11·151·2 113<1010.

令s=1,t=2.

r=3时,q=2·32·7-1=125=53, 此时|A1(q)|=q(q2-1)=1 953 000=23·32·53·7·31<1010.r=5时,q=2·52·7-1=349, 此时|A1(q)|=q(q2-1)=42 508 200=23·3·52·7·29 ·349<1010.r=11时,q=2·112·7-1=1 693, 此时|A1(q)|=q(q2-1)=4 852 557 864=23·32·52·7·112·47 ·349<1010.

当s=1,t=3时,r=3,q=2·33·7-1=377=13·29, 不是素数.

令s=2,t=1.

r=3时,q=2·3·72-1=293, 是素数. 此时|A1(q)|=q(q2-1)=25 153 464=23·3 ·72·73 ·293<1010.r=5时,q=2·5·72-1=489=3·163, 不是素数.

s=2,t=2,r=3时,q=2·32·72-1=881, 是素数. 此时|A1(q)|=q(q2-1)=683 796 960=25·32·5·72·11 ·881<1010.

b.q≡-1(mod 4).

由文献[1]知, π1=π(q+1),π2=π(q),π3=π((q-1)/2). 由于 7∈π(G)且dG(7)= 1, 此处讨论与a类似, 因此省去计算, 只给出结论.

情况37∈π1, 即q+1=2t·7s. 令q=2t·7s-1=4k-1. 可以得到G为A1(223),A1(27),A1(1 567).

情况47∈π3, 由于dG(7)= 1, 则|π(π3)|=2. 设(q-1)/2=rt·7s, 其中r≠2,7. 则q=2·rt·7s+1. 得到满足条件的群有：A1(43),A1(71),A1(239),A1(659),A1(743),A1(827),A1(1 163),A1(1 499),A1(1 583),A1(2 087),A1(127),A1(379),A1(491),A1(883).

c.q≡0(mod 2).

令q=2m. 由文献[1]知,π1={2},π2=π(q-1),π3=π(q+1). 由|A1(q)|=q(q2-1)<23m≤1010, 有m<12. 由于 7∈π(G), 得到m=3,6,9.

当m=3时,q-1=7. 当m=6时,q-1=26-1=32·7. 满足dG(7)= 1.m=9时,q-1=29-1=7·73, 满足dG(7)= 1.

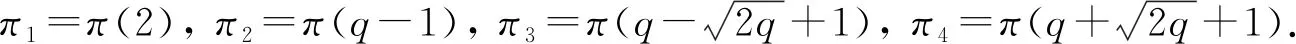
3) 若G为李型单群A2(4),2A2(9),C3(2),2A3(3),2A5(2),3D4(2),D4(2).

若G=A2(4), 此时,|G|=26·32·5·7, 由文献[3]知,π1={2,3,7},π2={5}. 不合题意.

若G=2A2(9), 此时,|G|=25·36·52·73. 不合题意.

若G=C3(2), 此时,|G|=29·34·5·7, 由文献[3]知,π1={2,3,5}, π2={7}. 不合题意.

若G=2A3(3), 此时,|G|=26·32·5·7, 由文献[3]知,π1={2,3,7},π2={5}. 不合题意.

若G=2A5(2), 此时,|G|=215·36·5·7·11, 由文献[3]知,π1={2,3,5},π2={7},π3={11}. 不合题意.

若G=3D4(2), 此时,|G|=212·34·72·13, 由文献[3]知,π1={2,3,7},π2={13}. 不合题意.

若G=D4(2), 此时,|G|=212·35·52·7, 由文献[3]知,π1={2,3,5},π2={7}. 不合题意.

4) 若G为李型单群C2(q), |C2(q)|=q4(q2-1)(q4-1)

5) 若G为李型单群G2(3k), |G2(3k)|=q6(q6-1)(q2-1)<314k<1010, 有k=1. 此时, 由文献[1]知,π1={2,3,7},π2={5}.dG(7)=2, 不合题意.

6) 若G为李型单群A2(q)(q是Mersenne素数), 即q=2p-1均为素数. |A2(q)|=q3(q3-1)(q2-1)<28p<1010, 有p=2,3. 此时q=3,7. 当q=3时, 7∉π(A2(q)). 当q=7时, |A2(7)|=73(73-1)(72-1)=25·33·73·19. 此时, 由文献[1]知,π1={2,3,7},π2={19}.dG(7)=2, 不合题意.

7) 若G为李型单群2A2(q)(q是Fermat素数). 即q=22n+1为素数. 由|2A2(q)|=q3(q3+1)(q2-1)

Ⅲ. 若G为散在单群M11,M22,J1,J2,J3,HS.

为方便, 下面列出这几个散在单群的连通分支，如表 1 所示.