加权空-谱主成分分析的高光谱图像分类
2019-06-10阿茹罕何芳王标标
阿茹罕, 何芳, 王标标
(1.西安培华学院会计与金融学院,西安 710065; 2.火箭军工程大学核工程学院,西安 710025; 3.96862部队,洛阳 471003)
0 引言
高光谱图像是由成像光谱仪获取的遥感图像,在农业研究、海洋监测和情报侦察等领域[1-3]应用较为广泛。高光谱图像较高的光谱维数和光谱分辨率为地物的精细分类带来了巨大的机遇[4-5],但是,数据量的急剧膨胀也给传统的分类识别算法提出了新的要求[6-8]。
随着光谱分辨率的提升,其相邻波段间的冗余性增强[9],严重影响了传统高光谱图像分类算法精度的提高。在训练样本有限的情况下,高光谱图像分类处理过程中还会遇到“维数灾难(curses of dimensionality)”现象[10],即随着维数的增加,高光谱图像分类精度会出现先升高后降低的现象。采用合适的降维方法将高维数据映射到低维空间,可以保留数据中的有用信息,摒弃其中的无用信息,从而减少数据量,避免维数灾难[1],提高分类精度[11-12]。
根据映射方法的不同,降维可以分为线性映射和非线性映射。线性映射的代表有: 线性判别分析(linear discriminant analysis,LDA)[13]和主成分分析(principle component analysis,PCA)[14-15]。非线性映射方法有: 局部保持投影(locality preserving projection,LPP)[16]和局部切空间排列(local tangent space alignment,LTSA)[17]等。
对于高光谱图像而言,其样本的分布在空间上具有连续性,仅仅基于光谱相似性的降维在很大程度上会使后续的分类性能下降[11]。引入空间信息可以有效抑制椒盐噪声的出现,提高图像分类精度,获得空间连续性较好的分类图像。因此,在对高光谱图像进行预处理时,应该结合高光谱的空间结构特性,充分考虑高光谱图像像元间在空间上的分布特性。基于此,本文提出加权空-谱主成分分析(weighted spatial spectral principle component analysis,WSSPCA)算法。
1 算法介绍
加权空-谱算法可以平滑高光谱图像,而PCA是经典的降维算法,具有快速高效的特点,将二者有效结合可以实现高光谱图像的降维,有效提高分类精度。
1.1 加权空-谱算法
在高光谱图像中,设像元点xi的空间坐标为(pi,qi),因此,该像元点xi的近邻空间可以用表达式定义为
N(xi)={x=(p,q)},p∈[pi-a,pi+a],q∈[qi-a,qi+a],
(1)
a=(w-1)/2,
(2)
式中w表示xi的近邻窗口的宽度,为奇数。近邻空间N(xi)中的像元点可以定义为xi,xi1,xi2,...,xis,s为xi近邻点的个数,即s=w2-1。
采用加权空-谱算法对像元点xi进行重构,即
(3)
νk=exp(-γ0‖xi-xik‖2),
(4)
式中:νk为近邻空间N(xi)中任一像元xik到中心像元xi的权重,其中参数γ0为光谱因子[18],若2个像元间的光谱曲线越接近,则权重越大。
该算法通过近邻窗口尺度w来调节近邻空间大小,引入空间特征; 同时,通过γ0调节像元的光谱值,调整像元间的相互影响程度,引入光谱特征。
采用图1方法对位于图像边缘或角落的像元进行预处理。图1中,高光谱图像中的一个像元用一个正方形格子代表,中心像元用浅灰色格子表示,相应的填补方式用深灰色格子表示。用与其近邻的像元点填补位于边缘或角落位置的像元点[19]。

(a) 正常位置 (b) 边缘位置 (c) 角落位置
1.2 WSSPCA原理
PCA作为一种有效的特征提取方法,应用于高光谱图像处理中可以降低高光谱图像数据间的冗余性,保留数据的主要成分,减小计算量[17]。WSSPCA算法综合了高光谱图像的空间信息和光谱信息后进行降维,可以大大提高高光谱图像的分类精度。
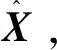
(5)
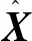
(6)
因此,S的特征值λ和特征向量ξi为
Sξi=λξi,(i=1,2,…,n)。
(7)
从中选取k个主成分分量构成高光谱图像的特征空间{u1,u2,...,uk},将重构后的数据投影到此特征空间中,即
(8)
对投影后得到的数据y采用最近邻分类器进行分类并计算分类精度评价指标。
1.3 基于WSSPCA算法的高光谱图像分类
基于WSSPCA算法进行分类的具体步骤如下。
输入: 高光谱图像数据X={x1,…,xn}T,X∈Rn×d,参数w和γ0。
步骤1: 根据式(1)确定高光谱图像X的近邻空间;
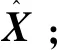
输出: 总体分类精度、平均分类精度和Kappa系数。
2 实验数据与算法验证
2.1 实验数据
本文选择PaviaU[20]和Indian Pines[7]图像数据集进行实验验证。
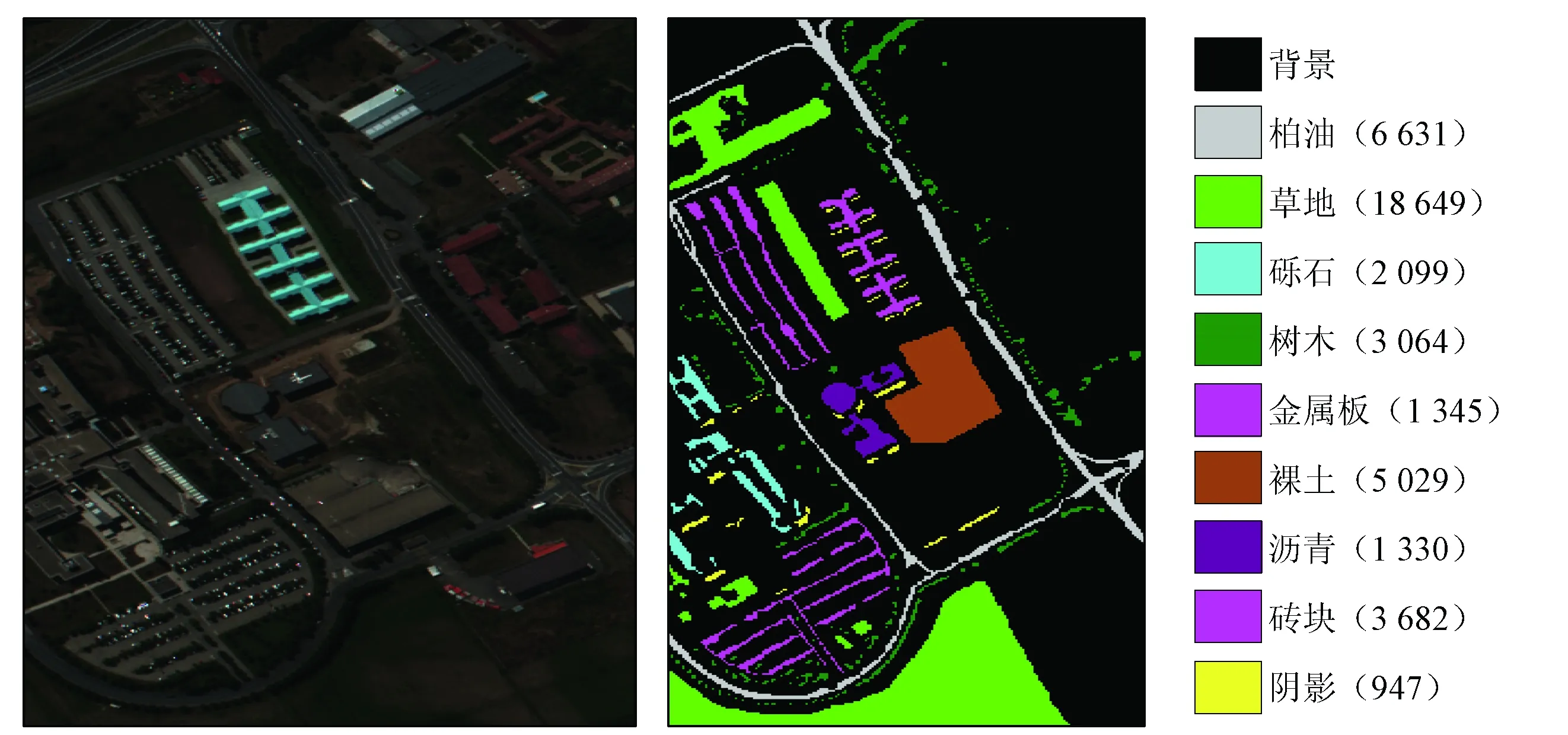
PaviaU数据集是由ROSIS传感器拍摄Pavia大学得到的高光谱图像。去除12个噪声影响最大的波段,剩余103个波段,每个波段包括610×340个像元点,具有9个类别的地物,图2(a)为PaviaU的B50(R),B27(G)和B17(B)假彩色合成图像,图2(b)为该数据地面真实地物类型及相应的图例。Indian Pines数据集是由AVIRIS传感器获取的,覆盖美国印第安纳州的一块印度松树地。去除水汽吸收及噪声波段剩下200个波段,每个波段包含145×145个像元点,具有16类不同类型地物,去除背景后剩下10 249个样本点。图2(c)为Indian Pines的B50(R),B27(G)和B17(B)假彩色合成图像,图2(d)为该数据地面真实地物类型及相应的图例。图例括号内为样本数。
(a) PaviaU假彩色图像 (b) PaviaU对应地物类型

(c) Indian Pines假彩色图像(d) Indian Pines对应地物类型
2.2 算法对比和验证
本文将所提的WSSPCA算法与经典的降维算法PCA,LPP以及不做降维处理直接进行分类的结果进行对比。对降维后的数据采用最近邻分类器进行分类。其中,直接采用最近邻分类器得到的结果作为基准线。采用实验分析的方法选取WSSPCA的参数w和γ0,LPP的权重矩阵T采用热核法进行构造,即
(9)
式中σ为热核参数。
本文所用高光谱图像的分类精度评价指标有: 总体精度(overall accuracy,OA),即被正确分类的像元总和除以总像元数; 平均精度(average accuracy,AA)指对所有地物完成分类后计算出的分类精度平均值; Kappa系数衡量分类结果的总体指标。这3个指标越高,则所用方法对高光谱图像的分类性能越好[6,12]。
3 实验结果及分析
3.1 PaviaU数据集
选取PaviaU数据集中每一类样本数量的5%作为训练样本,其余的样本作为测试样本。采用实验分析的方法选取PaviaU数据集的参数。从图3中可知,在PaviaU数据集上的最佳参数为:w=15,γ0=2.0。
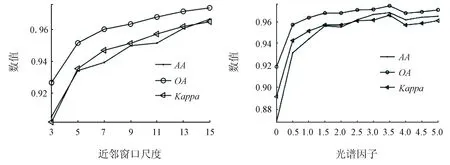
(a) 近邻窗口尺度与分类精度 (b) 光谱因子与分类精度
将每种算法重复进行10次分类实验求其平均。各种算法在不同低维子空间中的分类精度如图4所示。在训练样本相同的情况下,由不同算法得到的最高分类精度评价指标和所在低维子空间的维数如表1所示。

(a) AA与维数(b) OA与维数 (c) Kappa系数与维数

表1 在PaviaU数据集上由各种算法得到的最高评价指标及其对应的维数
由图4和表1可知,由WSSPCA算法得到的分类效果最好。其中,WSSPCA算法得到的OA最大值为96.69%,超出了基准线14.36%; Kappa系数最大值为0.955 9,超出了基准线0.193 8,而由PCA和LPP算法得到的分类结果均与基准线水平相近。图5显示了PaviaU数据库的训练样本、测试样本以及不做降维处理、采用PCA,LPP和WSSPCA算法得到的Kappa系数最大时对应的分类结果。

(a) 训练样本 (b) 测试样本(c) 基准线

(d) PCA (e) LPP (f) WSSPCA
3.2 Indian Pines数据集
在Indian Pines数据集上,随机选取每类样本的10%作为训练样本,剩下的样本作为测试样本。同样采用实验分析的方法选取WSSPCA算法中涉及到的2个主要参数。由图6可知,在Indian Pines数据集上,最佳参数设置为:w=9,γ0=1.0。
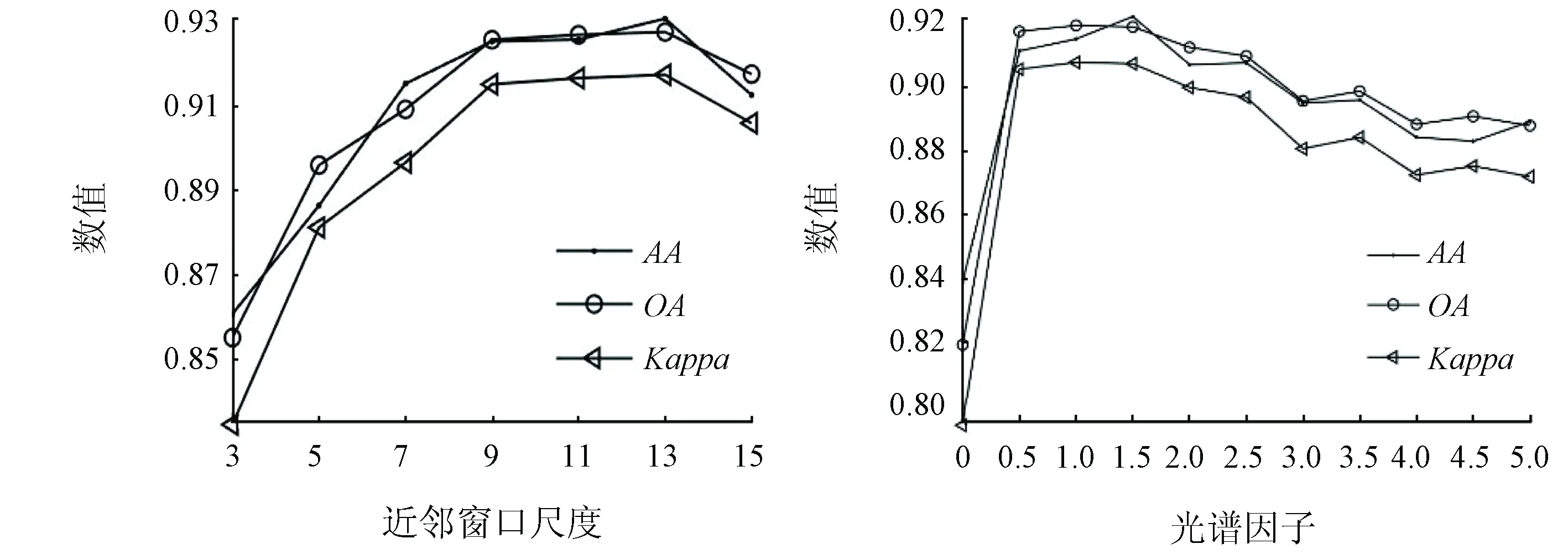
(a) 近邻窗口尺度与分类精度 (b) 光谱因子与分类精度
为比较各个算法的性能,实验中,随机选取每类地物样本的10%作为训练样本,当某类样本数小于100时则随机选取该类中的10个样本作为训练样本,其余样本作为测试样本。每种算法重复进行10次求平均值。为对比分析不同算法在不同维数下的分类效果,图7给出了在不同算法下AA,OA和Kappa系数与前100维低维子空间维数的关系。表2给出了不同算法在训练样本数相同的情况下最高分类精度评价指标和所在低维子空间的维数。
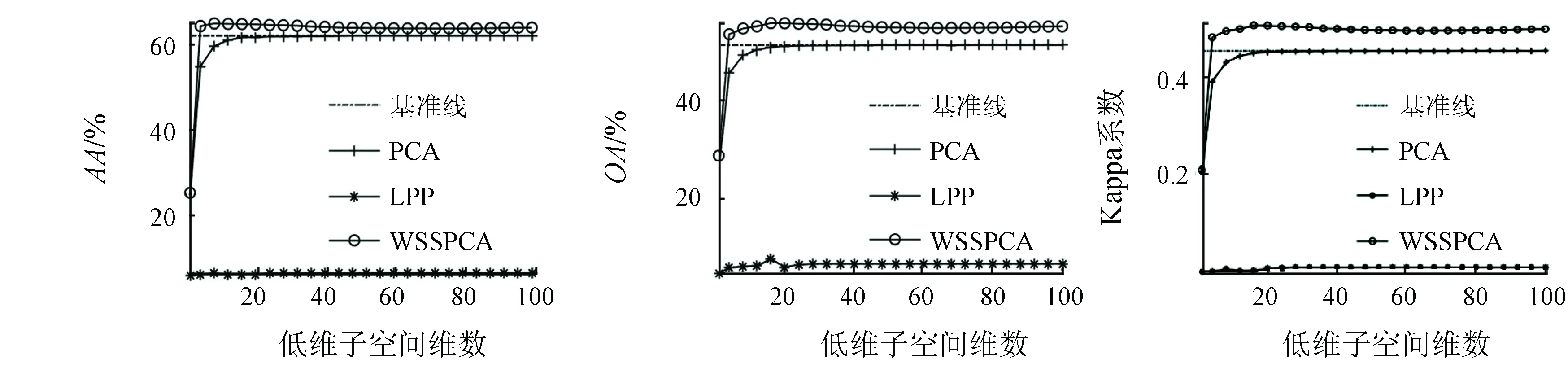
(a) AA与维数 (b) OA与维数 (c) Kappa系数与维数

表2 在Indian Pines数据集上由各种算法得到的最高评价指标及其对应的维数
由图7可知,由WSSPCA算法得到的分类结果明显优于PCA和LPP算法,由WSSPCA算法得到的分类精度最大值能够远远超出基准线,而由PCA和LPP算法得到的结果近似于基准线水平。这是因为WSSPCA算法有效利用了高光谱图像的空间和光谱信息,从而提高了分类精度。由表2可知,WSSPCA算法作为一种新型的空-谱联合降维算法,在训练样本相同的情况下,该算法的性能明显优于PCA和LPP算法。由WSSPCA算法得到的OA最大值为90.90%,超出了基准线17.93%。Kappa系数最大值为0.896 1,超出了基准线0.205 0。本文提出的WSSPCA算法使数据的可分性增强,分类效果较好。
图8显示了Indian Pines数据集的训练样本、测试样本以及不做降维处理、采用PCA,LPP和WSSPCA算法得到的Kappa系数最大时对应的分类结果,从图中可以看出由WSSPCA算法得到的分类结果更加平滑。
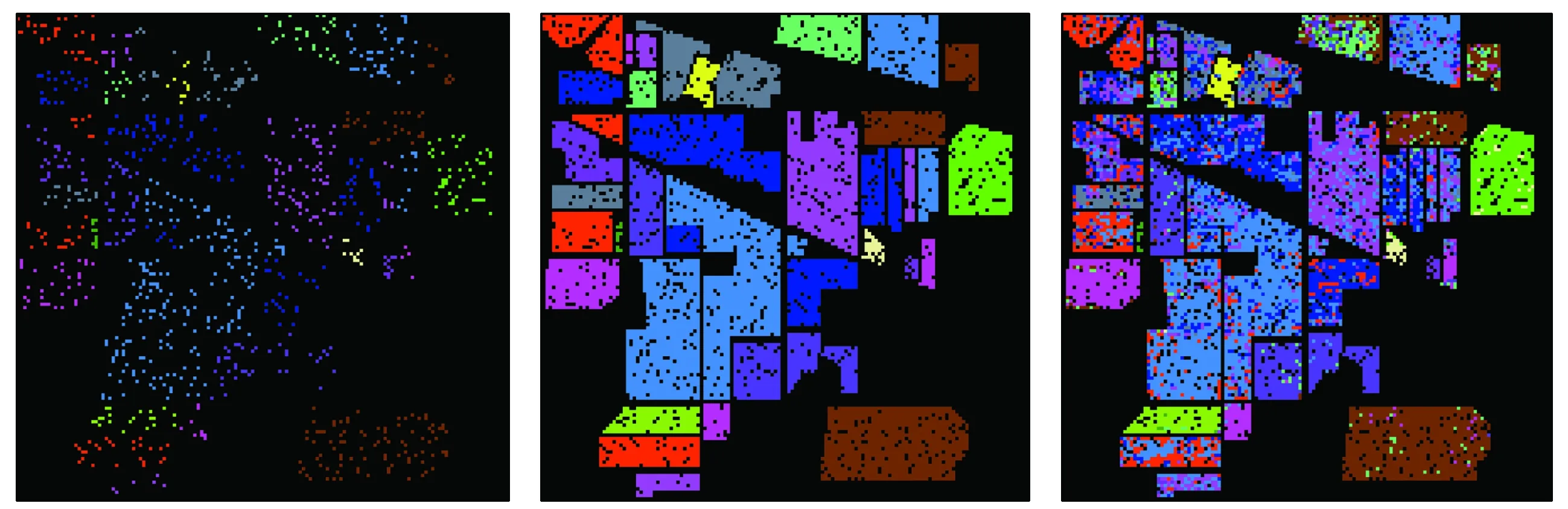
(a) 训练样本 (b) 测试样本 (c) 基准线
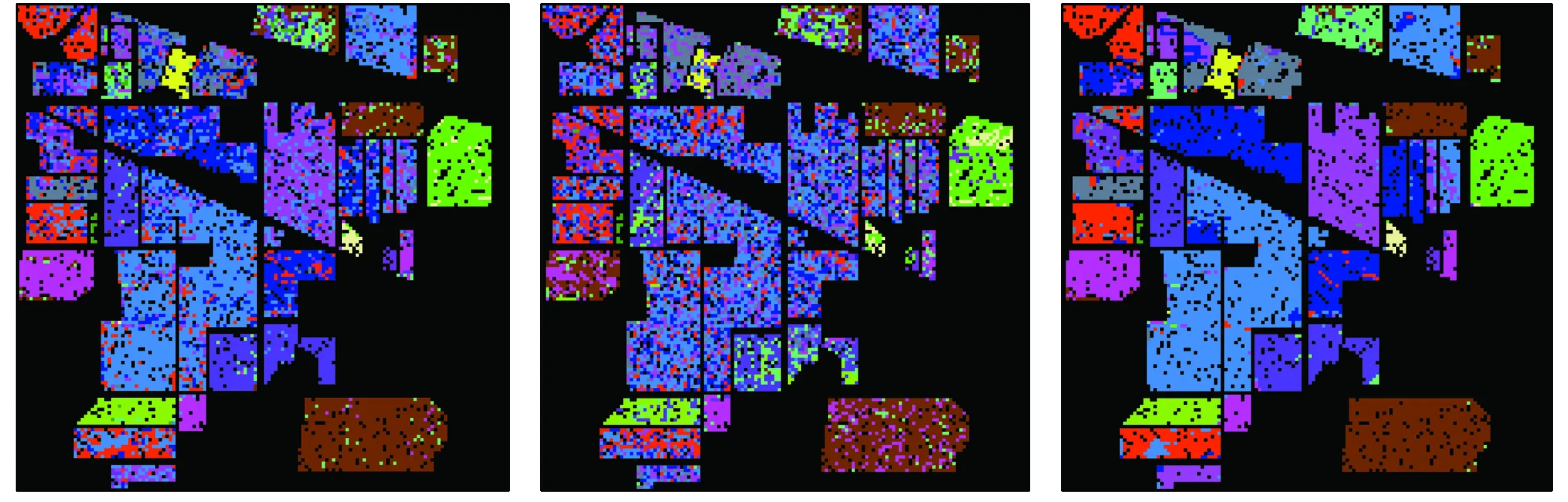
(d) PCA (e) LPP (f) WSSPCA
4 结论
本文提出了一种新的加权空-谱主成分分析(WSSPCA)降维算法,该算法不仅有效消除了高光谱图像中奇异点的干扰,而且减少了波段间的冗余信息,从而提高了高光谱图像的分类精度。通过在PaviaU和Indian Pines数据集上的实验结果验证了WSSPCA算法的优越性。
