基于RMNE方法的多尺度分割最优分割尺度选取
2019-06-10毛宁刘慧平刘湘平张洋华
毛宁, 刘慧平, 刘湘平, 张洋华
(1.北京师范大学环境遥感与数字城市北京市重点实验室,北京 100875; 2.北京师范大学地理科学学部地理学院,北京 100875)
0 引言
随着遥感技术的不断发展,高空间分辨率遥感影像层出不穷。面向对象的影像分割方法已成为高空间分辨率影像信息提取的重要手段。但是,目前面向对象的影像分割大多设定一个统一的分割尺度,对不同面积的地物易造成“过分割”和“欠分割”问题[1]。多尺度分割方法可以获得更全面的地物目标特征,逐渐成为研究热点。
针对多尺度分割最优尺度的选取,除依靠经验并结合目视选择最优分割尺度外,一些学者在通过统计计算确定最优尺度方面也开展了许多工作。Espindola等[2]利用影像对象的光谱标准差和Moran’s I指数,构建优度函数进行最优尺度选取; Woodcock等[3]利用对象的均值方差选取最优尺度,认为当影像分割对象的均值方差达到最大时,影像层中的纯对象最多,其所对应的分割尺度最优,但当存在过分割时均值方差也可能很大; 张俊等[4]提出用对象标准差和对象与邻域均值差分绝对值作为指标,构建函数模型选取最优分割尺度; 黄慧萍等[5]运用统计学方法,确定最大面积与分割尺度的关系,结合目视确定不同地物的最优分割尺度。目前已有的最优分割尺度选取方法大多数采用方差或标准差作为对象内部同质性的指标,只考虑对象的光谱统计特性,对于对象的空间分布特性考虑不足[6],没有充分利用高空间分辨率影像的特征,且方差和标准差不能很好地评价对象的同质性[7]; 用Moran’s I指数作为异质性指标,整个分割结果只得到一个异质性指数,忽略了局部对象与对象之间的异质性,具有一定的片面性[8]。
高空间分辨率影像具有更丰富的地物结构与形状信息以及更清晰的纹理特征[5]。已有研究表明,将纹理特征应用于高空间分辨率影像分割以及分类中可以显著提高分割效果和分类精度。Coburn等[9]将本湖影像的纹理信息参与分割和分类,林分的提取效果得到很大改善,分类精度最高提高了40%; Kim等[10]对超高分辨率影像进行面向对象分析,对比了单尺度与多尺度分割结果以及有无纹理特征对分割及分类结果的影响,结果表明辅助纹理特征角二阶矩阵和信息熵等的多尺度分割总精度比单尺度高6%,阐明了纹理的重要性; 林雪等[11]利用GF-1影像的多尺度纹理特征进行面向对象分类,表明结合纹理特征能更有效地提取地物信息,且纹理特征中的均值、协同性和信息熵等均能提高分割效果和分类精度。目前,应用纹理特征进行影像分割和分类较多,但在最优分割尺度选取方面应用信息熵和角二阶矩阵等灰度共生矩阵特征的较少。
针对上述情况,本研究提出用对象的纹理信息熵评价对象内部同质性,用与邻域均值差分绝对值评价对象之间的异质性,简称RMNE(the ratio of mean difference to neighbors(Abs)to entropy)方法,以2016年北京市位于城市边缘的研究区为例,基于6 m空间分辨率的SPOT6影像,采用面向对象的多尺度分割方法,利用RMNE方法选取最优分割尺度,并验证该方法的有效性。
1 研究方法
最优分割尺度指的是分割后影像对象与地物目标轮廓相当,大小接近,对象多边形既不能太破碎,也不能边界模糊,且光谱变异情况较小,影像对象内部同质性尽量高,不同类别对象之间的异质性尽量大。本研究依据此原则,利用纹理特征信息熵评价对象内部一致性,光谱特征与邻域均值差分绝对值评价对象外部差异性,构造RMNE指标进行最优分割尺度选取。通过多尺度的RMNE变化曲线确定最优尺度,并与目前常用的最大面积法和优度函数法对比,评价RMNE方法的有效性。基于RMNE方法的多尺度分割最优分割尺度选取流程如图1所示。

图1 研究流程
1.1 多尺度分割
多尺度分割算法的目标是在指定的与感兴趣的地物目标或空间结构特征相对应的尺度下,将影像分割成高同质的、互相连接的不同影像区域,与感兴趣的地物目标或空间结构特征相对应[12]。本研究运用eCognition8.7平台的多尺度分割技术,从像元开始,采用区域合并方法形成尺度(面积)不等的对象。相邻影像区域两两合并增长,合并的判断依据由相邻对象的异质性表达式值即阈值来决定。阈值可以看作是尺度参数[13]。该尺度参数的选取决定了图像分割停止的条件。若尺度参数过小,容易产生过分割现象,使同一地物被分割成多个对象; 而尺度过大,则容易产生欠分割现象,因此,分割尺度参数的选取成为影响图像分类精度的重要因子[14]。
1.2 RMNE计算及最优分割尺度选取
1.2.1 对象内部纹理信息熵
纹理特征能有效描述像元在空间上的排列、方向和组合方式[15]。与常用的图像特征相比,更好地兼顾了图像内在的组成结构。已有研究表明,纹理特征的参与提高了影像分割效果和分类结果[11,15]。纹理信息熵可以揭示对象内部空间分布上的复杂程度,故本研究采用对象的纹理信息熵衡量对象内部同质性,计算公式为

(1)
式中:ENT为对象纹理信息熵值;P(i,j)为灰度共生矩阵中第i行第j列处的概率值;N为灰度共生矩阵的行列数。
计算每一影像对象层的对象信息熵的平均值,作为该层的同质性指数,以此得到所有影像对象层的同质性指数。
为了消除量纲影响,将所得不同影像对象层的信息熵平均值进行归一化处理,取值范围为[0,1],即
(2)
式中:ENTmax和ENTmin分别为不同分割尺度对象层的信息熵平均值的最大值和最小值;F(ENT)为对象信息熵归一化后的值,F(ENT)越接近1,表示对象内部分布越复杂,即对象同质性越低;F(ENT)越接近0,表示对象内部分布越均一,即对象同质性越高。
1.2.2 对象之间异质性指数
对象与邻域均值差分绝对值可以揭示对象与每个分割层相邻影像对象的离散情况,由对象的光谱特征计算得到,计算公式为
(3)

计算每一影像对象层的对象ΔCL平均值,作为该层影像对象层的异质性指数,以此得到所有影像对象层的异质性指数。
已有研究表明该指数可以很好地揭示对象与对象之间的异质性[7]。为了消除量纲影响,同样将所得不同影像对象层的ΔCL平均值进行归一化处理,取值范围为[0,1],计算公式为
(4)
式中:ΔCLmax和ΔCLmin分别为不同分割尺度对象层的对象与邻域均值差分绝对值的平均值的最大值和最小值;F(ΔCL)为对象与邻域均值差分绝对值归一化后的值。F(ΔCL)越接近1,表示相邻对象之间越离散,即对象之间异质性越高;F(ΔCL)越接近0,表示相邻对象之间越依赖,即对象异质性越低。
1.2.3 RMNE
基于最优分割尺度原则,采用基于纹理的信息熵来评价对象内部同质性,与邻域均值差分绝对值来评价对象之间的异质性,由于合适的分割参数选择应该是结合了低的信息熵(即对象内部同质好)和高的与邻域均值差分绝对值(即对象之间异质性好),故本文将上述2个归一化后的值相除构建分割评价函数RMNE,计算公式为
(5)
RMNE值越大,代表该尺度得到的对象内部具有越高的同质性,对象之间具有越高的异质性。
1.2.4 最优分割尺度选取
在分割实验中,当分割尺度小于某种地物类别目标时,对象内含有相同的地物类别,对象信息熵较小,相邻对象之间属于同一个类别,从而具有空间相关性,离散程度较小,对象与邻域均值差分绝对值较小,故RMNE值较小; 当分割尺度大小等于某种类别目标时,对象内含有相同的地物类别,F(ENT)最小,相邻对象属于不同的类别目标,离散程度最大,F(ΔCL)最大,故RMNE值最大; 当分割尺度进一步增大时,对象内都会含有不同的地物类别,F(ENT)增大,与相邻对象之间的离散程度开始逐渐降低,F(ΔCL)减小,故RMNE值也开始减小。
综上,随着分割尺度的变化,RMNE值呈现由小到大再变小的波动过程,故多尺度分割的RMNE变化曲线的极值所对应的尺度就是最优分割尺度。因此,影像分割的最优尺度可以通过影像对象的RMNE值曲线来选择,结合目视判读或参考数据即可确定不同地物的最优分割尺度。
2 研究区概况及数据源
选取北京市朝阳区与顺义区交界处一地类丰富的地区为研究区,以检验本文方法的有效性(图2)。研究区内包含部分顺义中央别墅区、商业中心、道路、水体、草地和耕地等地物类型,总面积为90.63 km2。实验数据为2016年5月16日获取的6 m空间分辨率的SPOT6多光谱影像,含有蓝光(B)、绿光(G)、红光(R)和近红外(NIR)4个波段; 选择2016年6月14日的Google Earth影像作为实际地物参考影像。

图2 研究区影像
3 实验与结果
3.1 分割参数设置
在本研究中,将预处理(包括辐射校正、大气校正等)后的SPOT6影像的4个波段作为图像分割的输入波段,考虑到每个波段的信息都很丰富,所以将4个波段的权重都赋为1。根据经验,将实验中的光谱因子和形状因子权重分别设为0.7和0.3,紧致度因子和光滑度权重都设为0.5。在预实验分割中,当eCognition8.7软件分割尺度参数设置为100时,整个研究区仅被分割为29个对象,对象内部混杂,对象之间无明显边界,这样的对象已不具备研究意义,所以本文将分割尺度参数上限设置为100。选择分割尺度从10增至100,以10为步长的一系列尺度参数对研究区进行预分割,计算分割后每个尺度下的RMNE值,进而选取最优分割尺度。
3.2 RMNE计算结果及最优分割尺度选取
基于多尺度分割技术得到的不同尺度的影像对象,根据1.2节方法计算不同尺度的纹理信息熵值、与邻域均值差分绝对值和RMNE值,结果分别如图3所示。
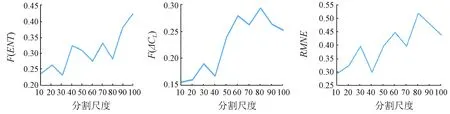
(a) 信息熵(b) 与邻域均值差分绝对值 (c) RMNE值
图3 RMNE方法计算结果
Fig.3ResultofRMNEmethod
由图3(a)可知,随着分割尺度的增大,对象信息熵值呈现3段先增大再减小的波动上升趋势,在分割尺度分别为30,60和80处形成3个极小值,当分割尺度大于80时F(ENT)急剧上升; 由图3(b)可知,随着分割尺度的增大,对象与邻域均值差分绝对值也呈现3段先增大再减小的波动趋势,当分割尺度分别为30,60和80时,对象与邻域均值差分绝对值出现了3个极大值点,当分割尺度大于80时F(ΔCL)迅速减小; 由图3(c)可知,随着分割尺度与地物类别目标大小之间的变化, RMNE值同样呈现先增大再减小的波动趋势,形成3个极大值点,对应的尺度分别为30,60和80。所以,由最优分割尺度选取方法及图3(c)可知,最优分割尺度组合为30,60和80。结合目视判断,尺度为30时,水体、道路、部分草地和水边林地的边界清晰,且能与其他相邻地物区分开,但大面积的耕地、建筑用地被分割的过于破碎; 尺度为60时,部分草地、建筑用地、耕地以及林地边界完整清晰,光谱差异较为显著; 尺度为80时,大面积的建筑用地和耕地具有完整的形状和边界,且容易与周围地物区分开。
3.3 方法比较
为了验证RMNE方法的有效性,分别采用最大面积法[5]和优度函数法[2]选取最优尺度,结果如图4所示。

(a) 最大面积法 (b) 优度函数法
由图4(a)可知,最大面积法得到的最优尺度区间分别为[20,30],[50,60]和[70,80],RMNE方法得到的最优分割尺度分别为30,60和80,处于上述尺度区间内,表明用RMNE方法获取最优分割尺度是有效的。而且相比最大面积法,RMNE法可以确定一个明确的尺度,更有利于后续实验。为了表明加入灰度共生矩阵的信息熵特征更有利于对高空间分辨率影像进行最优分割尺度选择,本文又将RMNE法得到的结果与优度函数法得到的结果进行对比,由图4(b)可以看出,优度函数法得到的最优分割尺度只有80。所以,仅用光谱特征来构建优度函数选取最优分割尺度对高空间分辨率影像来说具有一定的局限性,而加入了纹理特征,可以更好地选取最优分割尺度。通过与上述方法的对比分析可以发现,RMNE方法可以更好地选取多尺度分割的最优分割尺度。
3.4 多尺度分割结果及评价
由于RMNE方法得到的最优分割尺度组合为30,60和80,优度函数法为80,故按照这2种方法对应的最优分割尺度分别进行多尺度分割,得到如图5所示的分割结果。由图5对比可知,与优度函数法的分割结果相比,RMNE方法获得的影像对象边界与地物目标轮廓更接近,大小相当且与其他对象是可分的,具有更高的对象内部同质性以及对象间的异质性。

(a) RMNE法 (b) 优度函数法
为了对比RMNE方法和最大面积法的分割结果,取最大面积法得到的3个最优分割尺度区间的中值(25,55和75)进行多尺度分割。随机选取2种方法分割得到的4块不同地物类型(别墅、城镇居民地、商业用地和耕地)的影像对象进行对比,并以Google Earth影像作为参考,结果如图6所示。

(a) 区域1RMNE法结果(b) 区域1最大面积法结果 (c) 区域1Google Earth影像

(d) 区域2RMNE法结果(e) 区域2最大面积法结果 (f) 区域2Google Earth影像

(g) 区域3RMNE法结果(h) 区域3最大面积法结果(i) 区域3Google Earth影像

(j) 区域4RMNE法结果 (k) 区域4最大面积法结果 (l) 区域4Google Earth影像
可以发现RMNE方法分割得到的结果可以更好地对应实际地物对象,更具有地理意义,匹配度更高,故RMNE方法得到的最优分割尺度更优。
4 结论
本文提出了一种多尺度分割的最优分割尺度选取方法(RMNE),对研究区的SPOT6多光谱影像数据进行多尺度分割,通过与Google Earth影像对比可知,分割得到的影像对象大小与地物实际大小较为相符,实验结果验证了RMNE方法的有效性,并得出以下结论:
1)利用RMNE方法得到研究区的最优分割尺度组合为30,60和80,表明本文提出的采用对象的纹理信息熵和与邻域均值差分绝对值评价对象的同质性和异质性是有效的,对高空间分辨率遥感影像是适用的。
2)与最大面积法和优度函数法的结果进行对比可知,RMNE方法的分割结果更符合地物的实际大小和形状,具有明显优势,所以纹理信息的加入更有利于多尺度分割的最优分割尺度选择。
但是,本文的分割尺度从10开始,以10为步长,增加到100,尺度范围设置的略为宽泛。下一步将细化步长值,更精确地定位分割尺度。
