基于随机性测试的分组密码体制识别方案*
2019-06-10赵志诚赵亚群刘凤梅
赵志诚,赵亚群,刘凤梅
1.信息工程大学数学工程与先进计算国家重点实验室,郑州 450001
2.信息保障技术重点实验室,北京 100072
1 引言
密码分析作为一种被动攻击方法,是指在不知道解密密钥及通信者所采用的加密体制的细节的条件下,试图获得机密信息.根据所研究的对象,密码分析研究的对象主要包括两个部分:密码算法和密文.根据著名的Kerchoffs 原理[1]提出加密算法的公开不应该影响明文和密钥的安全,当前大多数密码分析方法也是在假设密码体制已知的前提下,展开对各种密码算法的分析.然而在现实中,被动攻击的一方通常仅能获取敌手的密文,这种情况下密码分析者只能开展唯密文攻击.因此识别密文的密码体制(以下简称密码体制识别)就成为了开展密码分析的一个前提条件.
近年来,AES 征集和评选、NESSIE 计划和Estream 计划等一系列公开的加密标准征集活动极大地带动了密码体制设计的发展[2,3].与此同时,针对当前各类密码体制的密码分析正持续成为研究热点.密码体制识别技术是密码分析的一个重要组成部分,主要研究在不同密码体制加密的密文中识别出具体的密码体制.许多具体的密码分析技术是专为某种密码体制设计的,或假设已知产生密文的密码体制.而在现实中,密码分析者得到的只是未知编制的密文,因此对于密码体制的识别是开展具体密码分析的前提条件.此外,密码体制抵抗识别的能力也可以衡量密码体制安全性,对于密码体制的设计与安全性评估具有积极的参考意义.因此开展密码体制识别相关研究,对于推动密码学的应用与发展有着双重的促进作用.
目前,密码体制识别方案的设计思路主要来源于统计学方法和机器学习技术[4].研究者认为,某一特定密码体制产生的密文与其他密码体制产生的密文在空间分布上存在一定的差异,从而尝试提取出能够刻画相应差异的特征,作为识别密码体制的依据.早期基于统计学的密码体制识别方法通过提取密文的各类统计指标进行比较,并给出识别结果.随着密码学的发展,各类密码体制混淆扩散能力不断提升,给密码体制识别带来巨大挑战.为此机器学习方法被引入密码体制识别任务中.基于机器学习技术的密码体制识别方案将特征视为一组属性、将识别任务等同于分类任务,在包含特征和算法标签的训练数据集上训练分类器模型,再用训练好的分类器对测试集数据(仅包含从密文中提取的特征)进行识别[4–7].基于机器学习技术的密码体制识别方案设计简单、表现稳定,且能处理数据之间的复杂关系,已经成为密码体制识别领域的研究热点.
密码体制识别最初的研究对象是古典密码体制.2001年,Pooja[8]设计了一种基于字母使用频率的古典密码体制识别方案,分析了包括置换密码、代换密码和维吉尼亚密码在内的主要的古典密码.随着现代密码技术的飞速发展,传统的基于统计学方法的密码体制识别技术逐渐失效.此时针对复杂且安全系数高的现代密码,国外研究者结合模式识别领域相关技术,设计了一系列基于机器学习方法的密码体制识别方案.2006年,文献[5]借鉴文档分类技术,提出了基于支持向量机的分组密码识别方案,考虑了对包含AES、DES、3DES、Blowfish、RC5 在内的五种密码体制的识别.2008年,Negireddy 等人[9]利用模式识别技术,对AES、DES、TDES、Blowfish、RC5 等密码体制在ECB 与CBC 模式下的加密密文做了区分实验.
2011年,Manjula 等人[4]提出了一种基于决策树分类器的密码体制识别方案,对包含2 种古典密码、1 种序列密码、6 种分组密码、2 种公钥密码的11 种密码体制进行了识别.2012年,Chou 等人[10]利用支持向量机技术分别对CBC 和ECB 两种工作模式下的加密密文进行区分,对ECB 模式下的密文进行了成功区分,对于CBC 模式下的密文则不能区分.2013年,De Souza 等人设计了一种基于神经网络的识别方案,研究了AES 最终轮候选密码算法的识别[5].2015年,吴杨等人[11]基于随机性测试采集了3 种密文特征,并在对AES、Camellia、DES、3DES、SMS4 五种分组密码体制的识别过程中使用了K-均值聚类算法.Sharif 等人[6,12]在其设计的分组密码体制识别方案中,比较了使用8 种不同的分类器模型的识别效果,其结果显示,组合分类器模型Rotation Forest 效果最佳.2017年,黄良韬等人[13]结合已有的密码体制识别研究成果,从密码体制识别方案设计和特征提取两大问题着手,提出一种基于随机森林算法的密码体制分层识别方案,其识别研究对象涵盖古典、分组、序列和公钥等现有主要的密码体制.该文给出一个较完整的密码体制识别问题的定义系统,并将密码体制的单层识别和分层识别统一于该系统下.
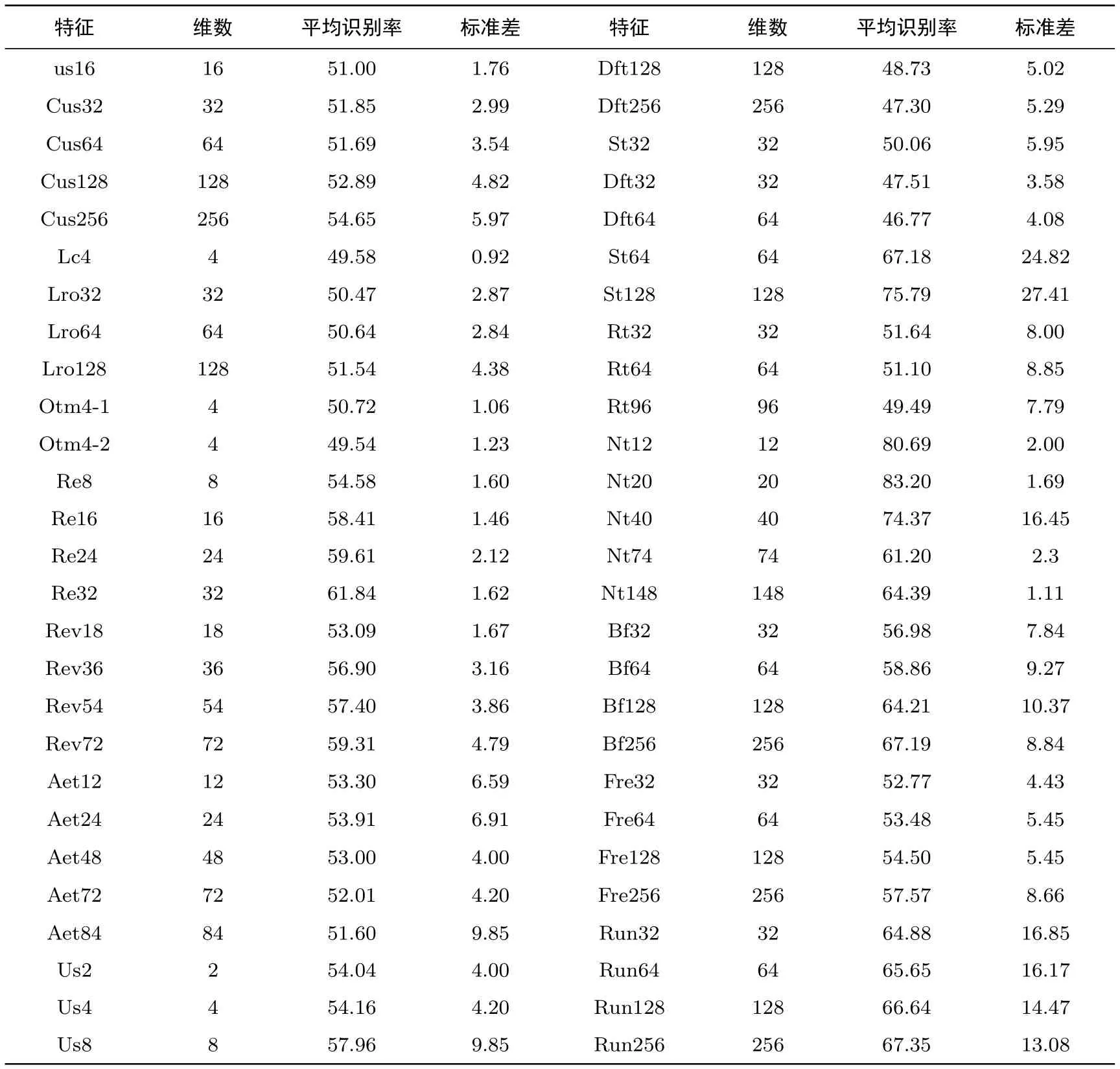
密码体制识别方案主要关注两个方面:密文特征的选取与挖掘、机器学习算法的选择.随着机器学习算法包括深度神经学习网络的发展,在算法选择方面,目前多数机器学习算法均有相应的程序包(例如R语言),研究者可以较为简易的对各类算法的分类性能进行比较.在密码体制识别任务中,特征提取对密码体制识别的成功率具有重要影响.由于分类算法直接对所提取特征进行处理,而密文数据自身通常具备较强的随机性质,因此提取出能有效地刻画密文信息的特征,成为识别任务中的关键环节.目前公开研究中的密文特征可以大致分为五类:
(1)计算字符、特定长度字节或比特等的熵[13];
(2)统计字符、特定长度字节、比特的概率[13];
(3)对密文开展随机性测试获得足够的返回值作为密文特征,如文献[11]基于码元频数检测、块内频数检测及游程检测设计了3 类表现比较优异的特征;
(4)将密文看成可变长的文档向量[5];
(5)将以上某几类特征组合成新的特征[10,13].

表1 部分文献中出现的密文特征Table 1 Typical features in some papers
观察表1,可以看到上述特征维数均在100 以上,个别特征维数已经超过10 万维.在机器学习领域,特征维数的提高通常会增加数据分析的存储开销与运行时间消耗.在机器学习领域,特征工程[14]的一个重要内容就是筛选信息量更多、灵活性更强的特征,从而能够在简单模型训练中也能得到优秀的结果.基于机器学习的密码体制识别任务,同样需要关注密文特征提取方式的改进以提高复杂数据环境下的识别效率.然而由于密数据通常具有较高的随机性,如何提取有效的密文特征、密文特征构建方法的创新,国内外关于该方面的公开研究较少,密文特征提取方式较为简单,因此特征所包含的密文信息有限.
分组密码算法以其易于标准化及运算速度快等特点得到广泛应用,其安全性也一直备受关注.目前关于分组密码算法攻击的分析集中于差分密码分析、线性密码分析和强力攻击[3].对分组密码体制识别的研究,可以为现实中的密码分析提供支持,同时也有助于密码安全性评估.本文主要关注AES、Blowfish和Camellia 等多种安全性较高且被广泛使用的分组密码体制的识别任务.基于随机性测试提出的一类新密文特征,并在由随机森林算法构成的分类器中开展分类训练和测试.
本文主要内容如下:第1 节介绍密码体制识别的相关概念和领域近年来的研究脉络与成果,对于已有的主要工作及其方法作简要分析;第2 节简略介绍了本文所提方案的主要构成部分;第3 节主要介绍基于随机性测试的密文特征提取方法;第4 节给出完整的密码体制识别方案;在第5 节展示实验结果并作分析;最后第6 节总结全文并展望后续工作.
2 密码体制识别基本原理
密码体制识别问题首先涉及到待识别密码体制集合即识别对象.当识别对象确定后,即可对具体的识别问题进行研究,给出相应的识别方案.而对方案效果的评价一般通过识别准确率给出.文献[13]将这些密码体制识别问题中的基本要素进行整合,给出密码体制识别及其识别方案的定义如下:
定义1(密码体制识别)考虑密码体制集合M={m1,m2,···,mN},其中N为密码体制数量.对于由任意密码体制m∈M加密生成的密文文件F,密码体制识别是指在可获取文件内容,但不知晓其密码体制m的情形下,通过某一识别方案J,以一定的准确率hJ识别出其密码体制m的过程,它由三元组Γ =(M,J,hJ)完全刻画.识别准确率在模式识别语意下有明确的意义,这里准确率hJ是评价密码体制识别方案的一种自然的度量.
定义2(密码体制识别方案)在密码体制识别问题 Γ 中,密码体制识别方案由三元组J=(oper,fea,alg)刻画,其中oper 表示方案进行密码体制识别的工作流程,fea 表示方案对密文数据所提取的特征或特征集,alg 表示方案采取的识别算法.
定义3(识别场景)在密码体制识别方案J中,任意待识别密码体制集合M即对应一种识别场景,记作qM.
根据识别场景和分类需求的不同,密码体制识别可以细分为簇分和单分.簇分是为了判断密文所属的密码体制在较大层次下的类别,如:判断密文是分组密码加密的还是公钥密码加密的,是分组密码中的CBC 模式还是ECB 模式等.单分则是确定密码体制的具体类别,如ECB 模式下128 bits 密钥长度下AES 与Camellia 所加密密文的识别.
在上述定义下,密码体制识别问题可记为Γ =(M,J,hJ),其中,密码体制识别方案由三元组J=(oper,feaM,CA)刻画,其中oper 表示方案进行密码体制识别的工作流程、feaM表示方案对密文数据所提取的特征(与待识别密码体制集合M相关),CA 为方案采取的分类算法,在本文中即为后续提到的随机森林算法.工作流程oper 由训练阶段和测试阶段的一系列步骤组成,以过程形式叙述如下:
过程oper.
训练阶段
步骤1.采集已知密码体制的一组密文文件F1,F2,···,Fn,其中n为文件个数;
步骤2.对文件内容数据进行特征提取,得一组特征集FeaM={,,···,},其中,i=1,2,···,n是维数为d的向量,称d为特征维数;
步骤3.记n个文件的密码体制标签(已知)形成一个n维向量Lab={lab1,lab2,···,labn},称二元组(FeaM,Lab)为带标签的数据;
步骤4.将带标签的数据(FeaM,Lab)提交分类算法CA,进行分类模型的训练.
测试阶段
步骤1.对一个待识别密文文件F的内容数据进行特征提取,得到d维特征fea;
步骤2.将特征fea 输入到在训练阶段训练好的分类模型中,后者给出密码体制识别结果,即密码体制标签lab.
上述示例展示了形式化定义的基于机器学习的密码体制识别方案,给定三元组J=(oper,fea,alg),即决定了一种密码体制识别方案.图1 是识别方案的训练与测试流程图.
3 特征提取
在机器学习领域,模型的质量通常由所选取的特征直接决定,特征对机器学习应用的效果有重要影响[15].本文引言已经介绍了密码体制识别任务中常见的密文特征提取方式,现有的密文特征存在识别成功率较低、维数较高的缺点.在文献[11]中,研究者运用随机性测试返回值构建的密文特征向量,对部分分组密码体制取得了较好的区分结果.文献[13]也选择了NIST 标准中的5 种随机性测试特征作为密文特征,并完成了多项密码体制识别任务.分析已有的研究结果可以发现部分随机性测试返回值确实可以反映密文中存在的差异,并以此完成密码体制识别任务.下面本文将从随机性测试的数学基础出发,介绍基于随机性测试的密文特征提取方法.
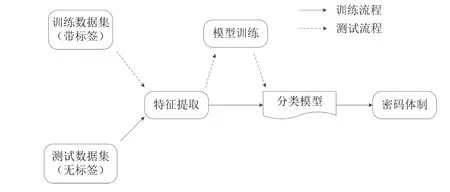
图1 密码体制识别方案流程图Figure 1 Flowchart of cryptosystems recognition scheme
3.1 随机性测试的数学基础
目前众多的随机性检测项目和方法,主要用于检测密码算法输出序列的统计特性,其中影响较为广泛的是美国商务部国家标准技术协会(NIST)于2001年5月公布的NIST FIPS140-2 标准[16]中定义的用于密码系统安全性度量的诸多随机性检测方案.测试一个序列的随机性,实质上是检验其是否是真随机的或与真随机序列之间的差距,而假设检验[17]是随机性测试的理论基础.在检验时,首先提出一个待检验的原假设,记作H0.相应地,与原假设相反的假设称备择假设,记作H1.例如,在随机性测试中一般设置原假设H0为:序列是随机的;备择假设H1:序列是非随机的.对于每个检验来说,若检验结果接受原假设即表明待检数据是随机的,否则认为待检数据是非随机的.检验的具体步骤如下:
步骤1.确定原假设H0和备择假设H1;
步骤2.根据H0的内容选取合适的统计量X,并确定其分布;
步骤3.按给定的显著性水平α,查统计量X所对应分布的分位数表,找出临界值,确定拒绝域;
步骤4.将由样本计算出的统计量X的值与查得的临界值进行比较,从而作出判断,即:若统计量X的值落入了拒绝域中,则拒绝H0,否则接受H0.
此外,假设检验会产生二类错误类型,如表2 所示.

表2 假设检验错误类型Table 2 Types of hypothesis testing errors
在实际应用中,衡量随机性的方法通常有2 种:门限值法和P-value 值法.这里以测试统计量X服从χ2分布为例来说明.
(1)门限值法.先做出分布的概率密度曲线如图2,根据给定的显著性水平α与相应的α分位点,再对统计量X与进行比较,确定是拒绝还是接受原假设.
(2)P-value 值法.同样作出χ2分布的概率密度曲线,先求出统计量X,然后计算从X到无穷的积分,将积分结果(即P-value 值,图中的阴影部分面积)与α进行比较,确定接受原假设与否.本文中讨论的随机性测试正是通过选取的测试统计量来计算P-value 值,将P-value 值作为接受原假设的强度,其含义是:真随机数的随机性比待测序列弱的概率.如果其值为1 则是完全真随机的,值为0 则是完全非随机的.对于显著性水平α,如果P-valueα,那么原假设被接受,序列是随机的,反之被拒绝,序列是非随机的.参数α也即是表2 中错误类型1 的概率,通常α的取值范围是[0.001,0.01],如图3 所示.

图2 卡方分布的概率密度曲线及其α 分位点Figure 2 Probability density curve of Chi-square distribution and its quantile of α

图3 卡方分布的概率密度曲线及其P-value 分位点Figure 3 Probability density curve of Chi-square distribution and its quantile of P-value
3.2 密文特征提取方法
同时在3.1 节中对随机性测试的介绍中也可以了解到,NIST 随机性测试对于序列随机性的检测具有较广泛的覆盖面,对于序列的全局或部分的随机性均有针对性的测试.本文在保证随机性测试返回值有意义的前提下,对密文进行分块或改变部分测试中的参数,再分别运行15 种NIST 随机性测试,分别得到了密数据集数量不等的测试返回值也就是第2 节中提到的P-value 值,这些返回值就作为密数据的特征数据.
采集密文特征数据过程中,为保证随机性测试返回值的有效性,在对密文分块时,对于测试的每个密文块均做到符合各随机性测试对序列长度的要求.设置密文分块个数有两个依据:(1)分块后的密文块大小必须符合随机性测试所需的序列长度要求(一些测试对于检测序列的长度要求较大,本文一般对密文不再分块,或者只分较少块);(2)在保证条件一的基础上,由于文件大小为512 kb,为了方便测试,所以选择的分块数都是512 的因子,这样在分块后,可以减少密文数据的损失.考虑到本文试图选取一些性能优良的低维特征,为此对于密文分块或特征维数均采取一定控制,一般不超过256 维.根据特征提取的方式和维数不同,上述特征可分为15 类共计48 种特征,其具体提取方式如下(设待检测序列长度为n):
(1)累积和测试(cumulative sums test).检测序列中的部分和是否太大或太小,太大或太小均被认为是非随机的,该测试返回2 个值.该测试要求待检测序列n100.分别将密文分为8、16、32、64和128 块,执行该测试提取得到的特征有:16 维、32 维、64 维、128 维和256 维共计5 种,分别简记为:Cus16、Cus32、Cus64、Cus128、Cus256.
(2)线性复杂度测试(linear complexity test).采用Berlekamp-Massey 算法[18,19]计算每个子序列的线性复杂度,并与真随机序列的复杂度作比较,以确定待测序列的随机性,该测试返回1 个值,要求待检测序列长度n106,且子序列长度M满足500M5000,因此最多只能将密文分为4 块.执行该测试得到的特征有:4 维共计1 种,简记为:Lc4.
(3)最长1 游程测试(longest run of ones test).检测序列中最长1 游程的长度与真随机序列中最长1 游程的长度是否近似一致,该测试返回1 个值,要求待检测序列长度n128.分别将密文分为32、64、128 块,执行该测试得到的特征有:32 维、64 维和128 维共计3 种,分别简记为:Lro32、Lro64 和Lro128.
(4)重叠块测试(overlapping template matchings test).统计待测序列中,特定长度的连续“1”的数目,并计算与真随机序列的情况偏离,如果偏离较大则认为序列是非随机的,该测试返回1 个值,要求待检测序列长度n106,考虑到测试对于序列的长度要求较大,对于该测试的密文序列未作分块.更改测试中参数的取值,得到特征有:4 维(根据参数不同设置分为2 种),分别简记为:Otm4-1 和Otm4-2.
(5)随机游走测试(random excursions test).检测序列中某个特定状态出现的次数是否远远超过真随机序列中的情况,如果超出较多,则认为序列是非随机的,该测试返回8 个值,要求待检测序列长度n106.将密文快分为1、2、3、4 块,执行该测试得到的特征有:8 维、16 维、24 维和32 维共计4 种,分别简记为:Re8、Re16、Re24 和Re32.
(6)随机游走测试变量(random excursions variant test).检测序列中某一特定状态在一个随机游程中出现的次数与真随机序列的偏离程度,如果偏离程度较大,则序列是非随机的,该测试返回18 个值,要求待检测序列长度n106.将密文平均分割为1、2、3 和4 块,执行该测试得到的特征有:18 维、36 维、54 维、72 维共计4 种,分别简记为:Rev18、Rev36、Rev54 和Rev72.
(7)近似熵测试(approximate entropy test).比较序列中长度分别为m-bit 与(m−1)-bit 串出现的频次,再与正态分布下的序列对比,从而确定序列随机性,该测试返回1 个值,要求待检测序列长度m (8)全局通用测试(universal statistical test).检测序列是否能在信息不丢失的情况下被明显压缩,通常一个不可被明显压缩的序列是随机的,该测试返回1 个值,要求待检测序列n387840.因此将密文平均分割为2、4 和8 块,执行测试得到的特征有:2 维、4 维和8 维共计3 种,分别简记为:Us2、Us4 和Us8. (9)离散傅里叶测试(discrete Fourier transform test).检测序列中的周期性质,并与真随机序列的周期性质比较,通过二者之间的偏离程度来确定待测序列随机性,该测试返回1 个值,要求待检测序列n1000.将密文平均分割为32、64、128 和256 块,执行该测试得到的特征有:32 维、64 维、128维和256 维共计4 种,分别简记为:Dft32、Dft64、Dft128 和Dft256. (10)连续块测试(serial test).检测序列中所有m-bit 组合子串出现的次数是否与真随机序列中的情况近似相同,如果是则序列符合随机性要求,该测试返回1 个值,要求待检测序列长度m (11)二元矩阵秩测试(rank test).将序列构造成若干矩阵,检测序列中固定长度子序列的线性相关性.如果线性相关性较小,则认为序列是随机的,该测试返回1 个值,要求待检测序列长度n>M×N,其中M和N分别为矩阵的行列数(NIST 默认M=N=32).将密文平均分割为32、64 和96 块,执行该测试得到的特征有:32 维、64 维和96 维共计3 种,分别简记为:Rt32、Rt64 和Rt96. (12)非重叠块测试(non-overlapping template matchings test).统计序列中,某特定模式出现的次数,并计算与真随机序列中的偏离,如果偏离较大则认为序列是不随机的.当重叠模块长度为5 时,该测试返回12 个值;当重叠模块长度为6 时,该测试返回20 个值;当重叠模块长度为7 时,该测试返回40 个值;当重叠模块长度为8 时,该测试返回74 个值;当重叠模块长度为9 时,该测试返回148 个值,该测试对待测序列未给明确规定,但是在测试样例中,序列长度为220.由于该测试不分块即可返回数十个返回值,故在本测试中不再对密文做分块.分别选择测试参数即重叠模块长度为:m=5,6,7,8,9,执行该测试得到的特征有:12 维、20 维、40 维、74 维和148 维共计5 种,分别简记为:Nt12、Nt20、Nt40、Nt74和Nt148. (13)组内频率测试(block frequency test).功能是检测待测序列中,所有非重叠的M-bit 块内的0 和1 的数量是否表现为随机分布,该测试返回1 个值,要求待检测序列n100 .将密文平均分割为32、64、128 和256 块,执行该测试得到的特征有:32 维、64 维、128 维和256 维共计4 种,分别简记为:Bf32、Bf64、Bf128 和Bf256. (14)频率测试(frequency test).功能是检测二进制序列中,0 和1 的比例是否均衡,该测试返回1个值,要求待检测序列n100.将密文平均分割为32、64、128 和256 块,执行该测试得到的特征有:32维、64 维、128 维和256 维共计4 种,分别简记为:Fre32、Fre64、Fre128 和Fre256. (15)游程测试(run test).功能是检测二进制序列中,游程分布情况是否符合随机序列的要求,该测试返回1 个值,要求待检测序列n100.将密文平均分割为32、64、128 和256 块,执行该测试得到的特征有:32 维、64 维、128 维和256 维共计4 种,分别简记为:Run32、Run64、Run128 和Run256. 作为上述特征性能的对比,本文选择了6 种在公开文献[4,7,12,13]中所使用的密文特征参与密码体制识别.下面是这些特征的具体提取方法: (16)将密文分别按分组长度为56 bits、128 bits、256 bits 分块,计算所有块中某一固定比特位的熵,形成维数与分块长度相同的特征,3 种特征分别记为:F_56b、F_128b、F_256b; (17)将密文分别按分组长度为9 bits、10 bits、11 bits 分块,计算不同组合形式的比特串出现频率,形成维数分别为256、512 和1024 的特征,3 种特征分别记为:F_256、F_512、F_1024. 本文首先基于上述特征开展密文分类、分组密码工作模式分类任务,以验证基于随机性特征在密数据分类任务中的有效性.在此基础上选择AES、DES、3DES、IDEA、Blowfish 和Camellia 等6 种分组密码作为密码体制识别研究对象.在方法构成层面,可分为两个主要部分:密文特征提取和密码体制识别分类器的构造.利用NIST 随机性测试程序包中的15 种随机性测试作为密文特征提取的方法基础,提取了45 种密文特征,同时也提取了部分已有的文献中提到的密文特征作为新密文特征的参照对象.本文采用随机森林算法构造密码体制识别分类器,并以提取到的各类密文特征数据作为分类器的输入,经过数据的训练与测试阶段,最终完成对密码体制的识别任务. 随机森林算法由Tin Kam Ho[20]提出,随后经由Leo Breiman 等人[21]对该算法做了扩展.随机森林是一个包含多个决策树的分类器,其输出类别是由个别树输出类别的众数而定(即所谓的投票方法).该算法对数据集的适应能力强,对于高维度的、离散和连续数据均能很好的处理,具有很好的抗噪声能力,而且算法本身简单且易于并行化.在分类实践中得到广泛应用.本文基于机器学习中的随机森林(random forest)算法构造分类器,所提识别方案分为两个部分:训练部分和测试部分.其具体算法流程展示如下: 基于随机森林的密码体制识别分类器 输入:密码体制数目k、每种密码体制加密密文数量S,维数为Dim 的密文特征fea=(x1,···,xDim)组成的样本集T=(C1,C2,···,Ck),其中Ci=(feai,1,feai,2,···,feai,S),Ci包含的是所有密码体制i加密的密文的特征集. 输出:分类结果密码体制A1,A2,···,Ak. 训练阶段 步骤1.输入密文特征集T,包含kS个样本,每个样本表示一个密文特征,每个特征有Dim 个属性,记为f1,f2,···,fDim;设定整数n 步骤2.采用有放回取样,随机在T中抽取M个样本,形成Bootstrap 样本集T∗,作为决策树根节点处的样本. 步骤3.随机从Dim 个属性中选择n个属性作为单棵树的候选属性,符合条件n≪Dim.再从这n个属性中采用某种策略(如信息增益)来选择1 个属性作为该节点的分裂属性. 步骤4.决策树形成过程中每个节点都要按照步骤2 来分裂,至不能够再分裂为止. 步骤5.重复步骤2–3 建立t棵决策树构成随机森林. 测试阶段 步骤1.对任一个输入的特征向量feai,j,记录其在每一棵树上输出分类结果. 步骤2.统计投票结果,票数最高的类别就是feai,j的类别标签. 本文中实验选择以由OpenSSL 密码库提供的AES、DES、3DES、IDEA、Blowfish 和Camellia 等6 种密码体制,其基本设置如表3.基于随机性测试的密文特征提取方法由C 程序实现,通过Rstudio 平台上的随机森林算法完成各类文本的分类.实验所用到的明文来自图片库[22]随机选择的图片拼接而成,随后被平均分割成1000 份,每份大小均为512 kb.对于不同的分组密码算法,凡未注明密钥设置的均使用固定密钥加密.实验过程中,待分析的密文样本量均为1000 份,每份大小均为512 kb.对实验数据(即对密文文件提取特征所得到的数据)进行重复随机子抽样验证(repeat random sub-sampling validation),每次抽样对每一密码体制生成的密文文件提取得到的特征样本,随机抽样75% 作为训练集,其余25% 作为测试集.以十折重复随机子抽样验证测试集识别的平均准确率作为识别效果的度量.对6 种密码体制的一一识别共计15 种识别场景进行了分类实验. 表3 7 种分组密码体制的具体参数列表Table 3 Parameter setting of 7 block ciphers 5.2.1 明密文与分组密码工作模式识别 在开展密码体制识别前,本文首先测试基于随机性测试密文特征在明密文识别和ECB 和CBC 两种分组密码工作模式识别任务中的有效性.其中,明密文识别实验是对ECB 模式下AES 加密密文与明文进行分类,分组密码工作模式识别则是对分别由ECB 和CBC 模式下的AES 加密密文的分类.为简化数据采集,该部分实验只选择基于上述15 种随机性测试的代表性密文特征作为分类时采集的特征数据. 表4 明文与AES 加密密文的识别结果Table 4 Recognition results of plaintext and ciphertext encrypted by AES 由表4 和表5 可以看出,多数基于随机性测试特征均能够以超过94% 的成功率实现对明密文的识别,以不低于82% 的成功率区分密文所使用的工作模式.考虑到明密文之间在统计上通常存在比较明显的差异且密码体制的工作模式对于密文随机性也具有较大的影响,上述实验初步验证了这些特征在密数据分析中的有效性. 5.2.2 分组密码体制识别 为进一步验证基于随机性测试特征在密码体制识别中的作用,采集54 种基于随机性测试的密文特征基础上,对6 种分组密码体质进行了一对一的分类实验,表6 展示各类特征在15 种识别场景下的平均识别成功率和识别成功率的标准差,其中平均识别率表示密文特征其密码体制识别性能的集中趋势,标准差则反映其识别性能的稳定性.图4 则以箱式图的形式展示基于随机性测试特征在不同识别情境下识别准确率的波动范围与中位数的分布. 表5 ECB 模式与CBC 模式下AES 加密密文的识别结果Table 5 Recognition results of ciphertext encrypted by AES ECB and AES CBC 表6 基于随机性测试的54 种密文特征的识别结果Table 6 Recognition performance of 54 features based on random tests 图4 54 种基于随机性测试特征在各识别场景下识别准确率的箱式图Figure 4 Boxplot of 54 features’ recognition accuracies 结合表6 和图4,可以发现,上述54 种密文特征的识别结果虽然存在较大差异,但总体上,多数特征能以高于随机(图3中的黑色水平线)的识别成功率区分6 种分组密码体制中的任意2 种密码体制,且部分特征具有较高的识别准确率.随着维数增大,Aet 系列特征的识别准确率波动幅度也在增大,Bf 系列、Cus系列、Fre 系列、Run 系列、Us 系列、Rev 系列和Re 系列特征的识别准确率随着维数增大而提高,Dft系列、Nt 系列特征识别准确率与维数的关系不明显,Rt 系列特征的识别准确率随着维数增大呈现出下降趋势.从实验数据来看,基于随机性测试的密文特征维数与其识别准确率并没有必然的关系.不同密码体制加密的密文其随机性存在差异,那么如果随机性测试可以反映出这种差异,其对应密文特征的识别准确率就会高.而提取密文特征时密文分块数、密文数据量显然对于随机性测试返回值的准确性(即反映密文随机性水平的能力)有一定影响,这种影响既可能是正向的也可能是反向的,其具体的作用机理有待进一步验证. 在对各密文特征在具体识别场景中的识别性能时,也发现部分特征的识别成功率与所识别的密码体制存在明显的相关性关系.如表7,Bf 系列特征(表中选取Bf128)对于3DES、IDEA 的区分,Us 系列特征(表中选取Us8)对于Camellia 的区分,Fre 系列特征(表中选取Fre256)对于3DES 的区分均要优于它们在其它识别场景中的表现.这几类特征对于某几类密码具有较高的识别率,表明部分密码体制加密密文确实存在一定的随机性差异,也说明了开展密码体制识别研究的可行性. 表7 部分密文特征的具体识别结果Table 7 Recognition results of part features in different situations(%) 5.2.3 与现有结果对比 为验证基于随机性测试的密文特征有效性,本文选择了6 种公开文献中提出的密文特征,并在相同实验条件下开展了密码体制识别实验.对比实验选择的特征分为两类:(1)基于比特熵的特征;(2)基于比特串概率的特征. 由于本文所提出的54 种基于随机性测试的密文特征识别性能差异较大,受篇幅所限,在表6 中识别性能相对较低的密文特征就不再与公开文献中的特征做对比.在表8 中,我们只选取基于随机性测试的6 种密文特征与其它已有的6 种密文特征做对比.可以发现,基于随机性测试的6 种特征虽然在识别准确率并不占优势,但是其特征维数通常较低.例如Nt20 特征的识别准确率与F_1024 的识别准确率相差5% 左右,但是Nt20 特征的维数仅为后者的1/50,这也显示出Nt20 特征具有数据存储量小的优势,对于提高大批量密数据的快速识别能力有一定的现实意义. 表8 部分基于随机性测试的密文特征与其它密文特征识别结果对比Table 8 NT series features and other features’ recognition results 5.2.4 实验结果的假设检验 在上述基于机器学习的密码体制识别方案中,分类实验将在同等条件下运行分类算法十次所得结果的平均值作为分类的最终结果.为验证分类方法的准确性,本文采用均值检验法独立两样本T-检验[23]对各实验结果进行检验.即:两组不同特征的识别准确率数据,检验一组总体均值是否大于对照组总体均值,这里假定两个总体独立地服从正态分布.相应的假设检验问题为:H0:µ1=µ2⇔H1:µ1>µ2. 将上述实验中十折的每一折数据记录下来并作为一组数据,同时生成一组以为均值的随机数数据.设置显著性水平为0.01,检测两组数据的均值是否相等,验证实验数据的真实性.经检验,在显著性水平为0.01 的情况下,本文实验中涉及的所有数据的假设检验结果均符合要求. 本文在已知密文条件下,以AES、DES、3DES、IDEA、Blowfish 和Camellia 等六类典型分组密码为识别分析对象,通过改变随机性测试算法的提取方式与参数设置,提出了一系列分组密码算法识别的新特征.以上述所提取的特征为分类依据,并在OpenSLL 密码库、VS2012 以及R 语言环境下进行了实验仿真.实验表明,基于随机性测试的密文特征能够以较高的识别准确率完成明密文识别和密码体制工作模式的识别.对于难度较高的分组密码体制识别,本文提出的54 种特征绝大多数也具有一定的识别性能,部分特征的识别性能接近或达到了目前已有的密文特征的水平.与现有的多数密文特征比较,基于随机性测试的密文特征具有更低的维数.此外,通过比较实验数据,发现一些密文特征在不同识别场景下的识别准确率与密码体制存在一定的相关性,即对于某几类密码体制具有较高的识别准确率.基于随机性测试的密文特征,在密码体制识别中具有一定的有效性,因此作为改进密文特征提取的一个新思路值得进一步研究探索. 本文的实验对象包含的密码体制种类有限,基于随机性测试的密文特征在密码体制识别中的适用性及其识别效果也需要结合密码学中的相关理论做出严谨的解释.同时对于随机化密钥设置和CBC 模式下的分组密码体制识别也需要进一步的研究探索.后续工作中,将针对更多识别情形下,基于随机性测试的密文特征的提取方法,进一步改进识别分类器的算法以提高密码体制识别效率.4 识别方案
5 实验结果与分析
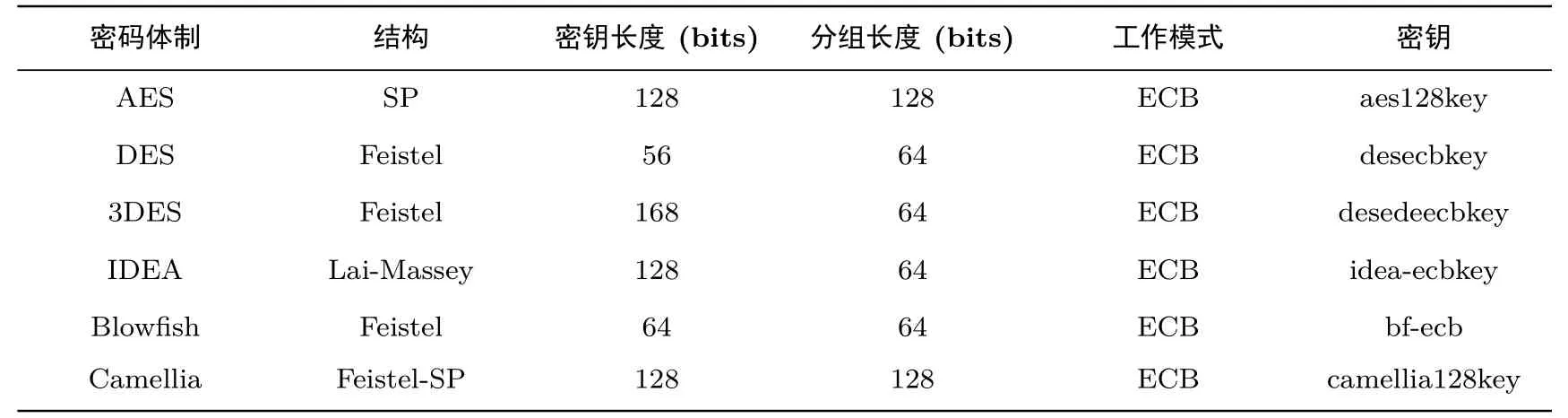
5.1 实验对象及相关设置
5.2 实验结果与分析


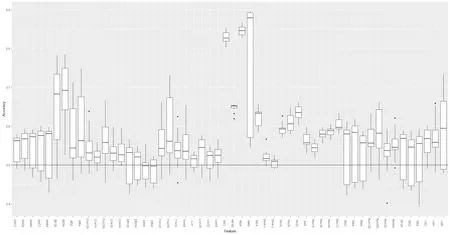
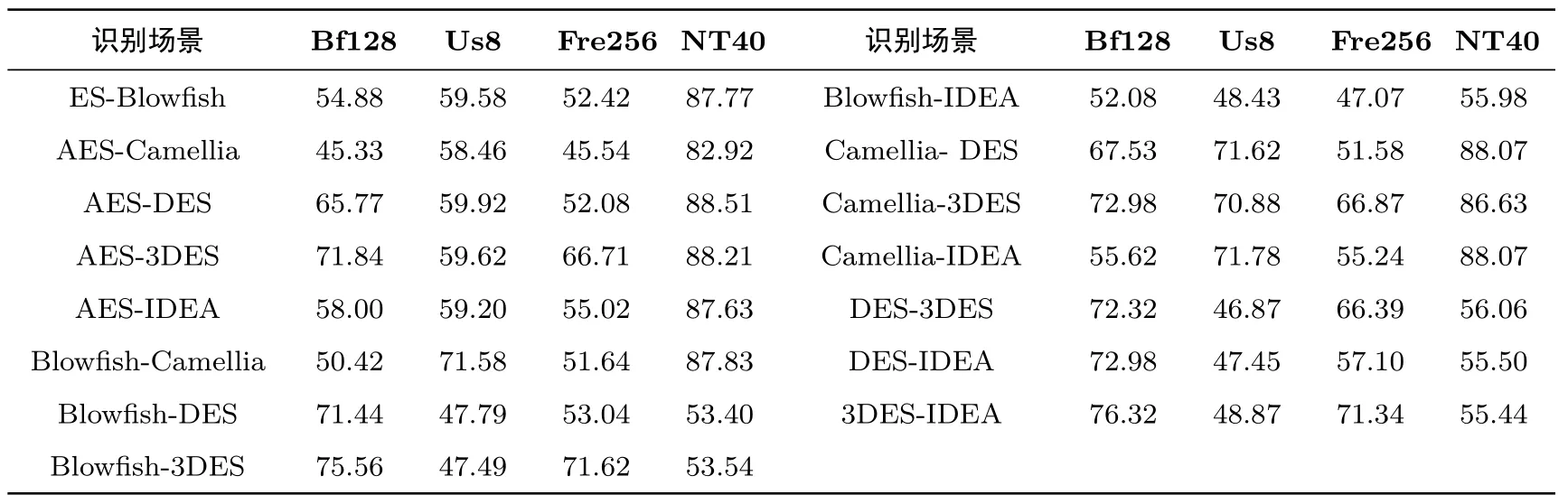

6 总结与展望
