云环境下多方保密计算最大值、最小值及其统计学应用*
2019-06-10李占利陈立朝陈振华刘娅茹
李占利,陈立朝,陈振华,刘娅茹
西安科技大学 计算机科学与技术学院,西安 710054
1 引言
在信息化、网络化的时代,隐私保护变得日益重要,越来越多的合作计算需要在保护隐私的基础之上进行,把这种计算模式可归结到安全多方计算的范畴中,这是由华裔科学家、图灵奖获得者姚期智[1]教授率先提出的,需要参与合作计算的每一方利用自己的隐私数据合作计算出一个共同的函数,要求任何一方都得不到其他参与者的隐私数据,也不能利用中间计算结果推导出他人的保密数据.安全多方计算具有广泛的实际应用,如:保密质量评估[2]、保密的数据挖掘[3–6]、保密的计算几何[7–10]、保密的统计分析[11]、保密科学计算[12]、安全云外包计算[8,13–15]等.在保密的科学计算中,已经研究了百万富翁问题[16–18]、安全集合操作[19–26]、保密排序[27–29]、保密计算最值[30]等问题.
保密求最值(最大值、最小值)在保密科学计算中是非常重要的问题,在统计学中也有重要的应用.保密求最值是指:多个参与者想要知道他们当中数据的最值(包括最小值和最大值),但是任何一方都不愿意让其他人获知自己的隐私数据.该问题具有很多应用场景,并且也有重要的应用价值.
场景一:有多个国家想知道他们当中导弹数量的最大值、最小值,但是任何一个国家必然不会直接将自己国家导弹的数量公布于众,要解决这个问题,其数学模型就是多方保密计算最值.
场景二:要统计某一群体当中拥有的最多财富与最少财富,从而获知该群体的贫富差异,但是群体中每个人用的财富多少是隐私,一般不会轻易告诉他人,因此,该问题也要归结为多方保密求最值问题.
上述场景一属于保密军事问题,场景二属于保密的民生统计问题,实际中更多类似的场景都可归结为此类问题,但目前关于此类问题的研究不是很多,效率不是很理想,影响实际应用.此外,由于已有的关于保密求最值是通过参与者之间进行交互完成的传统模式方案,用户(参与者)的计算成本较高,不利于实际执行.本文首次将保密求最值问题放在了云计算平台下实现的,也是首次给出了可抗量子攻击的多方保密求最值的解决方案.
1.1 相关工作
早在1982年,Yao[1]率先提出安全多方计算,并给出了安全多方计算的通用方案—姚氏混淆电路,由于计算复杂度是输入数据规模的指数级别,显然不切合实际.随后,Goldreich 等人[31,32]也给出了安全多方计算的通用解决方案,然而从方案的计算效率方面考虑,他们指出该方案针对具体的安全多方计算问题是不实际的,但是,Goldreich 等人引入了安全多方计算的安全性定义和证明的模拟范例,并证明了在半诚实参与者条件下一般的安全多方计算问题是可解,也证明了存在部分恶意参与者的情况下的安全多方计算问题同样也是可解的,认为研究具体安全多方计算问题是有必要的,这不仅激励了研究者的研究兴趣,还为后续针对具体问题的研究打开了理论局面.Goldreich 等人推动了安全多方计算研究的发展.
对于安全多方计算最大值、最小值问题,到目前为止已有的研究方案不多,2017年窦家维等人[30]首次给出了安全多方计算最小值的解决方案,方案是基于编码、ElGamal 同态加密算法,并结合秘密共享以及门限密码体制设计的,紧接着,以多方保密计算最小值协议为基础,经过改造可以多方保密计算最大值.在该方案中,协议1 不可抵抗含拥有私钥参与方的合谋攻击;协议2 是基于编码、ElGamal 同态加密和秘密分割等方法设计的,由于采用了密文分割技术,并要通过不经意传输进行实现,协议的通信复杂度和计算复杂度骤增;窦等人紧接着巧妙采用ElGamal 门限密码体制设计了协议3,较协议1 和协议2 其安全性提高了,但是由于所有的协议都是通过参与者之间进行交互完成计算的,而且协议是多个参与者交互完成,计算能力仅仅依靠参与者自身,而在解决复杂问题时参与者自身计算能力往往是有限的,同时效率也较低.云计算具有强大的计算能力和存储能力,正好可以用来解决参与者计算能力有限、效率低等问题,从而尽可能为参与者降低计算成本.
窦等人的方案虽然是首次解决了最小值以及最大值问题,然而该方案中的所有协议都是基于离散对数数学难题的加密技术,一旦量子计算机得到应用,那么基于数论假设的离散对数等数学难题将在多项式时间内是可解的,从而基于数论难题假设的同态加密算法构造的协议将会是不安全的.1996年,Hoffstein 等人[33]提出NTRU(number theory research unit)算法,是一种基于多项式环的公钥密码体制,其安全性基本是与求解最坏情况格上困难问题等同的,因此被认为可以抵抗量子攻击,该公钥密码体制具有公私钥生成高效、易于并行计算等特点[34–36].
针对上述问题,本文采用0-1 编码,将保密数据隐藏于对应编码的数组中,接着采用多密钥NTRU 全同态加密算法,将最大值、最小值问题架构在云计算平台上进行解决,设计相应的安全多方计算协议.然后,将协议简单地应用于统计学中,解决了多方保密计算极差的问题,协议简洁高效且安全.
1.2 本文贡献
本文是首次将多方保密计算最值问题架构在云计算平台下进行解决,具体的贡献如下:
(1)将保密数据通过0-1 编码,从而把数据隐藏在所编码的0-1 数组中,再结合多密钥NTRU 全同态加密算法,提出了一种解决保密计算最大值、最小值的问题的新方案,并证明了方案的安全性,然后应用新方案设计了多方保密计算极差的协议.
(2)首次提出将多方保密求最大值、最小值问题架构在云计算平台下的解决方案,由于采用云外包技术,为用户节省了很大的计算成本,因而效率较高.
(3)本文在云计算平台下设计的协议,由于采用多密钥NTRU 加密算法,不仅完全抵抗任意数量的合谋攻击,而且还可以抵抗量子攻击.
2 预备知识
2.1 安全多方计算的安全性定义
(1)理想模型
所谓理想模型,就是存在一个可相信第三方(trusted third party,TTP),他不会欺骗任何参与方,也不会向任何一个参与方透漏其他参与方的任何信息.假设现在有N(N2)个参与方P1,P2,···,PN,借助TTP 完成一项计算,只需要N个参与方将自己的保密数据x1,x2,···,xN告诉TTP,TTP 计算f(x1,x2,···,xN),只将计算结果分别告诉参与方.由于N个参与方仅仅知道f(x1,x2,···,xN),而不知道其他任何额外的消息,因此这样的一个安全多方计算协议是最安全的(称为理想协议),实际中任何保密计算协议的安全性都不会超过理想协议的安全性.
由于实际的安全多方计算是没有TTP 的,因此在现实中设计的安全多方计算协议如果泄露的信息不比在理想模型下多,那么就被认为是安全的.
(2)半诚实参与者
安全多方计算协议的执行环境有两种,即半诚实参与者模型和恶意参与者模型[31,32],半诚实参与者是指在执行协议过程中,会忠实地严格遵守协议本身的步骤,但是这些参与者也会保留协议执行过程中的各种计算结果,企图通过这些中间结果推导出其他参与方的输入数据信息.
本文涉及的参与者和云服务器都是半诚实的,因此本文设计的协议都是在半诚实模型下执行的,而对于恶意模型下的协议,可使用Goldreich 等人[31,32]提出的通用转化方法直接由半诚实协议转化得出,要研究恶意模型下的协议,往往是先研究半诚实模型下的协议,再研究恶意敌手如何攻击这种协议,找到避免恶意攻击的方法,将其添加到协议中,从而就形成恶意模型下的协议,因此研究半诚实模型下的协议有着重要意义.所以我们在本文中只给出半诚实模型下的协议,同时也给出在半诚实模型下对应的安全性模拟范例.
(3)云计算环境下多方计算的安全性定义
鉴于本文的协议都是在云计算平台下设计的,计算过程有不全可信第三方(云服务器)的参与,且参与方数量多于2,和传统模式的安全两方计算的安全性定义有所不同,因此我们在这里给出在云计算平台下的安全性定义.
设N个参与方P1,P2,···,PN分别拥有保密数据x1,x2,···,xN,Cloud Sever(CS)是云服务器,f(x1,x2,···,xN)为概率多项式函数,π是计算f的协议.这N+1 方须在不泄露xi(i∈[N])的情况下,合作计算f(x1,x2,···,xN)=(f1(x1,x2,···,xN),···,fN(x1,x2,···,xN)).目的是为使每一位参与方Pi(i∈[N])分别得到fi(x1,x2,···,xN,在整个过程中,不论合谋与否都要必须确保任何一方都无法获取其他方的保密输入数据xi.
将每一位参与方Pi(i∈[N])在执行协议π的时候得到的视图记为viewi(x1,x2,···,xN),CS 的视图记为view0(x1,x2,···,xN).在这个系统中存在两类合谋,一类是参与方Pi(i∈[N])中若干方合谋,但至多仅有N−1 方合谋;另一类是CS 与部分参与者Pi合谋,最坏情况下,CS 至多和任意N−1个参与者合谋想要获得剩下一方的保密数据.将第一类合谋情况下的视图记为viewI(x1,x2,···,xN)(其中,I⊆[N],且2|I|N−1).Pi将第二类合谋情况下的视图记为viewI′(x1,x2,···,xN)(其中,CS∈I′⊆[N]∪{CS},且2|I′|N).Pi发送给CS 的数据分别为E(xi),CS 的计算结果为E(x1,x2,···,xN)(即CS 获得的输出).
定义1在云计算环境下,我们说协议π保密计算了f(x1,x2,···,xN),如果存在多项式时间的算法(模拟器)Si、S0、SI、SI′使得表1 中所有式子同时成立.

表1 云计算环境下多方计算的安全性Table 1 Security definition of multiparty computation in cloud environment
2.2 多密钥NTRU 全同态加密[37]
文献[38]中提出了同态加密的概念,同态加密是指直接通过在密文上进行计算以达到明文某种运算的目的.同态加密经历了半同态到全同态的发展,半同态是指在密文上仅能进行某一种操作(即加法或者乘法),以达到明文的运算的目的,而全同态可进行两种运算操作(加法和乘法),本文的协议利用了全同态加密,下面给出NTRU 全同态加密方案.
(1)多密钥NTRU 全同态加密方案
KeyGen.:给定安全参数κ,产生(pki,ski,ek)(i∈[t]),其中pki和ski分别是每个用户的公、私钥,ek 是公开的求值密钥.公、私钥的具体构造如下:
给定安全参数κ,B有界的误差分布χ=χ(κ)和n次多项式ϕ(x)=ϕκ(x),且χ=χ(κ)是在多项式环R=Z[x]/ϕ(x)上的分布,给出一个有界的多项式f′,g∈χ,并且设f=2f′+1,显然有f≡1(mod2)成立,令h=2gf′为公钥,f为私钥(如果在环R中f的逆不存在,须重新取f′).
Enc.:给定公钥pki和消息mi,产生密文ci=(pki,mi)(i∈[t]).
任取有界多项式si,ei∈χ,mi∈M={0,1}(明文消息mi编码成多项式,其系数为0 或1).输出密文ci=hiei+2ei+mi.
Dec.:给定t个用户的私钥ski和一个密文c∗∗,布尔电路C,其中c∗∗为多密钥全同态操作所得密文,输出相应的明文Dec(sk1,sk2,···,skt,c∗∗)=C(m1,m2,···,mt).
计算u=c∗∗f1·f2·ft∈R,以及u(mod2),输出明文C(m1,m2,···,mt).这里要求u的系数在集合中.关于多密钥NTRU 全同态加密方案各个算法的构造以及安全性分析和全同态性详见文献[37]中3.2 节、3.3 节和3.4 节以及文献[39].
Eval.:对于布尔电路C,输出t个密文的同态运算操作结果为:

上述Eval.是一个全同态操作,计算t个密文的和或积,这个同态运算可以看成两个新密文和的和或者积.其中看成是由t个密文中的一部分同态运算的结果,是剩下的一部分密文同态运算的结果,同时这两个新密文分别对应一套公钥,记为K1和K2.
(a)加法同态:直接计算cadd=c∗∗=+;
(b)乘法同态:分为两种情况,如果K1K2=∅,则cmult==×否则,设K1K2={pki1,···,pkir},则用如下方法计算cmult.
对于全部τ∈{0,1,···,logq},取sτ,eτ∈χ,计算γτ=hsτ+2eτ+2τf,令ek=(γ0,···,γlogq)∈对于j∈[r](r为K1和K2交集的势),定义的二进制表示,以及ekij=(γij,0,···,γij,logq),令迭代到最后有
总之,上述t个密文是由|K1K2| 个公钥产生的,cadd和cmult的解密密钥为K1K2对应的私钥:这里fKi(i=1,2)表示Ki中所有公钥对应的私钥乘积.这与解密算法Dec.是一致的,即当有λ个公钥产生的密文进行同态运算时,解密的私钥为f1f2···fλ,与同一个公钥下对应不同的密文参与同态的次数无关.这里
(2)多密钥NTRU 全同态加密算法的解密
为了清楚给出多个密文同态操作后的解密,我们给出N=2 时的解密过程.设c1和c2是两组完全不同的公钥h1和h2产生的密文:c1=h1s1+2e1+m1,c2=h2s1+2e2+m2,对应的私钥分别为f1和f2,则用共同解密密钥f1f2解密cadd=c1+c2和cmult=c1c2可简化如下.
(a)加法同态的解密运算:

(b)乘法同态的解密运算:

对于N3 的情形,即多个密文的全同态操作后的解密运算和N=2 是类似的.
3 问题的描述与转化
3.1 问题描述
设有N个参与方P1,P2,···,PN,分别持有一个保密数据x1,x2,···,xN,他们想计算这N个参与方的最大值、最小值,但每一位参与方都不想泄漏自己的私有数据信息.
3.2 问题转化
在本文中,我们先让每一位参与者Pi将自己的私有数据xi按照本文给出的0-1 编码方法编码一个0-1 数组,然后结合多密钥NTRU 同态加密算法解决了本文提出的最值问题.
0-1 编码:设x1,x2,···,xN∈{v1,v2,···,vm} =U,这里U是一个全序集,即满足v1 这样,Pi的保密数据xi与编码的数组Xi=(αi1,···,αim)是对应的,对N个数组X1,X2,···,XN作乘积,即将数组对应的元素相乘,得到新的数组Y=(y1,y2,···,ym),其中再将数组Y的所有元素相加,得到即: 由Xi的构造式(1)以及计算k的表达式(2),易证明有下面命题成立. 命题1如果对于每一个xi(i∈[m]),按照式(1)构造数组Xi,并以式(2)计算k,则 min{x1,x2,···,xN}=vk 为了更清楚地呈现命题1,我们给出一个实例. 例1设全序集U={1,3,5,7,9,11},P1,P2,P3分别拥有x1=3,x2=7,x3=9,遵循命题1 计算这三个数的最小值,具体见表2. 表2 命题1 的实例Table 2 Example of Proposition 1 根据命题1 可计算若干个数据中的最小值,若直接按照命题1 进行计算,显然所有数据的隐私性没有得到保护,因此,需要利用同态加密算法将每个数组进行加密,再保密计算k.这里对数组加密指的是对数组中每一个元素加密. 协议1 云计算环境下多方保密计算最小值Input:P1,P2,···,PN 各自所持的秘密数据x1,x2,···,xN ∈{v1,v2···,vm} =U,其中v1 分析:(1)不合谋的情形,由于使用多密钥同态加密算法,每个参与者各用自己产生的公钥加密自己的私有数据,无法获得别人的私钥,因此,任何人得不到其他参与者的秘密数据. (2)合谋的情形,本文方案中的合谋分为两类,参与者之间的合谋和参与者与CS 的合谋.先讨论前者的合谋,不失一般性,假设有N−1 个参与方P1,P2,···,PN−1合谋想要知道PN的秘密数据E(XN)=(E(αN1),···,E(αNm)),方案整个过程中,任何人无法获得别人的私钥,因此直接从加密PN的数组中无法获得XN=(αN1,···,αNm),从而得不到xN;如果通过协议1 中步骤3–5 联合解密得到N方的最小值vk=min{x1,x2···,xN} 小于N−1 方合谋的最小值vk′=min{x1,x2···,xN−1},即k 本文将上述协议1 所给的全序集合编码方法稍作修改,就可以改造出多方保密计算最大值的协议,P1,P2,···,PN各自所持的秘密数据x1,x2,···,xN∈{v1,v2···,vm} =U,其中v1>v2>··· >vm,即要求全序集中元素从大到小排列,编码修改如下: 为了更加直观地呈现出解决多方计算最大值问题的转化过程,也呈现出与协议1 的紧密关系,给出实例2 如表3 所示. 例2设全序集U={11,9,7,5,3,1},P1,P2,P3分别拥有x1=3,x2=7,x3=9,遵照式(3)的编码,然后计算这三个数的最大值,具体见表3. 表3 最大值问题转化实例Table 3 Transformation example of maximum problem 由于最大值问题与最小值问题的转化过程是对称的,因此,将问题架构在云计算平台下,结合多密钥NTRU 全同态加密算法构造相应协议如下. 协议2 云计算环境下多方保密计算最大值Input:P1,P2,···,PN 各自所持的秘密数据x1,x2,···,xN ∈{v1,v2···,vm} =U,其中v1 >v2 >··· >vm.Output:vk =max{x1,x2···,xN}1 每个参与方Pi(i ∈[N])通过式(3)将自己的保密数据xi 编码成数组Xi.2 每个参与者Pi 执行多密钥NTRU 加密算法中密钥生成系统,产生公钥pki =hi 和私钥ski =fi.各自使用自己产生的公钥加密已编码的数组,得到:E(Xi)=(E(αi1),···,E(αim)).3 每个参与者Pi 将自己自加密的数组发送给CS,利用多密钥NTRU 全同态计算E(k)=∑m j=1∏N i=1 E(αij),并将E(k)发送给任意一个参与者,不妨设为P1.4 P1 收到CS 发来的E(k),计算u1 =E(k)f1,P1 将u1 发送给P2.5 P2 收到u1,计算u2 =u1f2 =E(k)f1f2,直到PN 计算k =un =uN−1fN =E(k)f1f2···fN,此时vk =max{x1,x2···,xN}.6 PN 将最大值vk =max{x1,x2···,xN} 告诉其他参与方. 由于协议2 是在协议1 的基础上构建起来的,仅改变了协议1 中全序集元素的排列顺序和相应的编码方式,两个协议是完全对称的,根据协议1 后面的分析,所以协议2 的正确性是自明的. 定理1在半诚实模型下,协议1 是安全的. 证明:由于本文协议1 是架构在云计算平台的,因此要证明定理1,需要构造模拟器Si、S0、SI、SI′使得表1 中所有式子都成立.为了节省篇幅,在这里给出不合谋情形中模拟器Si的构造过程,以及合谋情形中模拟器的构造过程,模拟器S0、SI的构造过程省略. (1)构造模拟器Si. 在此协议中,fi(x1,x2,···,xN)=fj(x1,x2,···,xN)=vk或vk,其中ij.假设等号成立,构造模拟器Si.Si接受xi,fi(x1,···,xi,···,xN)作为输入,按如下方式进行: (a)Si随机取N−1 个数使得:fi(x1,···,xi,···,xN).并按照3.2 节编码方法(1)对进行0-1 编码,不失一般性,编码如下: (c)Si得到这些之后,计算 (d)按照协议1 的解密过程解密E(k∗),得k∗,从而得到最小值vk∗. 于是有: 同理,用类似的方法可构造模拟器S0使得: (2)构造模拟器SI′. 不失一般性,设N−1 个参与方P1,P2,···,PN−1与CS 合谋,想要得到PN的保密数据xN,此协议中,fi(x1,x2,···,xN)=fj(x1,x2,···,xN)=vk或vk,其中ij.假设等号成立,构造模拟器SI′(I′={P1,P2,···,PN−1,CS}).P1,P2,···,PN−1的输入和输出为 {(x1}[N−1]和{fi(x1,x2,···,xN)}[N−1],CS 将得到{E((xi)}[N]作为输入,输出为将{(x1}I′,{E((Xi)}[N],{fi(x1,x2,···,xN)}I′作为输入,按如下方式进行: (a)模拟器SI′随机取一个数,使得1]).并按照3.2 节编码方法(1)对x1,x2,···,xN−1,进行0-1 编码,不失一般性,编码如下: (b)用(X1,···,XN−1,)进行模拟,按照协议1,将数组(X1,···,XN−1,)进行加密,得到(E(X1),···,E(XN−1),E()). (c)SI′得到这些之后,计算 (d)按照协议的解密过程,解密E(k′),得到k′,从而得到vk′. 可得SI′({xi}I′,{fi(x1,x2,···,xN)}I′,E(x1,x2,···,xN))={{xi}[N−1],{E(xi)}[N],E(k′),k′,vk′},viewI′(x1,x2,···,xN)={{xi}[N−1],{E(xi)}[N],E(k),k,vk}. 由于vk′=fi(x1,x2,···,xN−1,)=fi(x1,x2,···,xN−1,xN)(i∈[N−1]),则vk=vk′,从而k=k′,E(k)(k′).所以: SI′({xi}I′,{fi(x1,x2,···,xN)}I′,E(x1,x2,···,xN))viewI′(x1,x2,···,xN) 由上述证明过程可知,即使 CS 和P1,P2,···,PN−1合谋,也得不到PN的隐私数据,因为viewI′(x1,x2,···,xN)只是由P1,P2,···,PN−1和CS 的输入{xi}[N−1],{E(xi)}[N],E(k′),以及自身获得的输出{fi(x1,x2,···,xN)}[N−1],E(k)得到的,不含PN的任何消息. 同理,CS 不参与合谋,仅P1,P2,···,PN中若干方合谋,用构造SI′类似的方法可以构造模拟器SI使得: SI({xi}I,{fi(x1,x2,···,xN)}I)c=viewI(x1,x2,···,xN) 协议2 与协议1 在转化方法以及协议设计上是完全对称的,采用类似证明定理1 的方法和过程即可证明协议2 是安全的,因此下面定理是成立的,本文省略其证明过程. 定理2在半诚实模型下,协议2 是安全的. (1)理论分析 由于文献[30]中的协议是首次多方保密解决最值问题的方案,与本文的协议1 和协议2 有相似之处,都是采用编码的转化方式,同时都是结合同态加密算法设计的.因此本文将协议1 和协议2 与窦等人的协议进行比较.文献[30]方案中基本运算是模乘运算,本文的基本运算是模乘与模加运算,而模加运算相对于模乘的运算成本是可忽略的.为了便于比较,不考虑各个方案中准备阶段以及随机数选取的计算开销,因此我们以模乘次数作为衡量计算开销的标准.文献[30]中方案采用ElGamal 加密体制,模数为大素数p,模乘运算记为Mp;本文方案模取φ(x)=xn+1、q和2,模乘运算记为Mφ,p,2,且假设编码的长度都统一为m,N表示参与方的数量,m表示全集的势. 计算开销:设参与者P1,P2,···,PN所持有保密数据分别为x1,x2,···,xN∈U,|U| =m.本文协议1(由于协议2 与协议1 完全对称,这里仅分析协议1)中每一方Pi(i∈[N])需要m+1 次模乘运算,因此本文协议1 共需要N(m+1)Mφ,p,2次模乘运算;文献[30]中协议1 参与者Pi(i∈[N])最多需要m次加密和2m次模乘运算以及需要y次解密,而ElGamal 加密算法每次加密需要2 logp次模乘运算,每次解密需要logp次模乘运算[16],因此文献[30]中协议1 共需(2Nm+y)logp+2Nm(Mp)次模乘运算;文献[30]中协议3 协商构造公钥过程中需要mlogp次模乘数运算,参与者Pi(i∈[N])最多需要m次加密,需要2Nmlogp次模乘运算,解密过程中需要(Nm+y)logp次模乘运算,则文献[30]中协议3共需要(3Nm+m+y)logp(Mp)次模乘运算.由于文献[30]中的协议2 在其协议1 的基础之上下采用密文分割和不经意传输技术,效率低于其协议1 的效率,因此不对其协议2 进行效率分析. 通信开销:衡量通信复杂度的指标有两种,协议交换信息量的比特数和通信轮数,在安全多方计算研究中,通常是采用通信轮数来进行衡量.本文协议1 加密后将密文发送给CS 需要N次通信,解密过程中需要N次通信,将解密结果告诉其他参与方需要N−1 次通信,因此本文协议1 共需要3N−1 次通信.在文献[30]的协议1 中Pi(i∈[N−1])将加密后密文发送给PN需要N−1 次通信,PN解密后将结果告诉其他参与方也需要N−1 次通信,因此整个过程需要2(N−1)轮通信;在文献[30]的协议3 中协商构造公钥和机密过程中各需要N−1 次通信,解密过程需要y(N−1)次通信,因此文献[30]的协议3 共需要(y+2)(N−1)次通信,这里y表示最小值. 性能:以协议是否适合云计算平台、能否抗量子攻击、抗合谋情况作为衡量性能的指标,其中× 表示不具有此性能,✓表示具有此性能,≮表示部分具有此性能. 综合以上分析,本文协议与文献[30]中协议1 和协议3 效率比较如表4 所示,性能比较如表5 所示. 表4 协议效率比较Table 4 Efficiency comparison among protocols 表5 协议性能比较Table 5 Performance comparison among protocols 根据表4,本文协议1 计算开销最低,尽管通信开销高于文献[30]协议1,但是通过表5 看出文献[30]协议1 只能部分抗合谋,而且既不适合云计算平台,也不能抗量子攻击.通过表4 和表5,与文献[30]协议3 相比,除了可以完全抵抗合谋外,本文协议1 适合云计算平台,可抗量子攻击,显然更优. (2)仿真实验 由表4 可以看出,文献[30]中的协议1 比协议3 的效率高.因此,本文将文献[30]中的协议1 与本文协议1 所采用的加密算法通过Java 编程语言实现,比较耗时情况.本次实验过程中,采用的计算机配置如下:操作系统为Windows 7 旗舰版,CPU 为AMD A6-3240M 1.5 GHz,内存为4.00 GB. 文献[30]中的协议采用ElGamal 加密算法,模为p,模乘运算记为Mp;本文协议采用NTRU 加密算法,模取φ(x)=xn+1、q和2,模乘运算记为Mφ,q,2,实验过程中,取ElGamal 加密算法中参数p与NTRU 加密算法使用的域参数n(即φ(x)=xn+1 中的n)的位数相同,并且本实验将NTRU 加密算法中模q固定为1024 bits.这里将p和n都分别取128 bits、256 bits、380 bits、512 bits,在这4 组参数下,分别计算一个模乘运算Mp和Mφ,q,2的平均耗时,每组参数下,每个模乘运算取7 个实验结果,求每个模乘的平均耗时,得到表6,其中表6的第一列表示n(p)的位数(bit),第2–3 列分别表示在不同模数下一个模乘运算Mp和Mφ,q,2的平均耗时(ms). 根据表6,进一步计算出表4 中计算开销所需要的logp(Mp)和Mφ,q,2的结果,并画出logp(Mp)和Mφ,q,2随模数变化趋势图,如图1 所示.横轴为不同的模数(bit),纵轴表示ElGamal 和NTRU 两种加密体制在不同模数下分别对应logp(Mp)和Mφ,q,2平均耗时(ms).其中ElGamal 中为logp(Mp),NTRU中为Mφ,q,2. 通过图1 可以看出,ElGamal 加密算法中的logp(Mp)的平均耗时比NTRU 加密算法中的Mφ,q,2的平均耗时多,即logp(Mp)>Mφ,q,2,且随着模数线性增加.由理论分析所得表4 中的数据,得到本文协议1 的耗时低于文献[30]中协议1 的耗时,因此本文协议1 的效率高于文献[30]中两个协议. 表6 不同模数下的一个模乘的平均耗时Table 6 Average consuming-time of modular multiplication under different modulus 图1 log p(Mp)(ElGamal)与Mφ,q,2(NTRU)的平均耗时对比Figure 1 Comparison of average consuming-time between log p(Mp)(ElGamal)and Mφ,q,2(NTRU) 极差是一个简单而又常见的统计量,表示一组数据中最大值与最小值的差.而多方保密计算极差是指多个参与方P1,P2,···,PN分别持有一个数据x1,x2,···,xN,他们想要保密计算出所有数据的极差,但是不想让任何人知道自己所持数据的任何信息.具有重要应用价值和前景,如:要统计某一群体当中贫富差距,从而获知该群体的贫富差异,但是群体中每个人用的财富多少是隐私,一般不会轻易告诉他人,因而,此问题的数学模型就规约为多方保密计算极差. 如果分别直接调用一次协议1 和协议2,就会分别计算出最大值与最小值,这样不符合解决问题的需求.本文以协议1 为基础,构造多方保密计算极差协议.不妨设x1,x2,···,xN∈{1,2,···,m},这里x1,x2,···,xN< 利用与3.2 节类似的转化方法计算 按照式(4)的编码方法和式(5)转化方法,容易得到下面命题2. 命题2如果对于每一个xi(i∈[N]),按照式(4)构造数组Xi={βi1,βi2,···,βim},并以表达式(5)计算l,则max{x1,x2,···,xN}=m−l. 因此x1,x2,···,xN的极差为range=m−l −k=m−(l+k),从而问题转化为保密计算l+k.为了更加直观,我们给出实例3. 例3设全序集U={1,2,3,4,5,6},P1,P2,P3分别拥有x1=2,x2=3,x3=5,根据上述转化方案计算这三个数的极差,具体见表7. 表7 极差问题的转化实例Table 7 Transformation example of range problem 由于统计问题在实际应用中样本可能比较庞大,因此多方保密计算极差问题仍然架构在云计算平台上进行解决,下面给出具体协议. 协议3 云计算下多方保密计算极差Input: P1,P2,···,PN 各自所持的秘密数据x1,x2,···,xN ∈{1,2,···,m},这里x1,x2,···,xN 协议3 整个过程中每位参与者需要2m次加密和m次解密,总共需要3Nm次模乘运算,需要进行3N−1 轮通信.由于协议3 在协议1 的基础之上进行改造的,而且使用的加密算法具有语义安全性,因此利用证明定理1 的类似方法即可证明下面的推论,这里不再具体进行证明. 推论在半诚实下,多方计算极差问题的协议3 是安全的. 保密科学计算中多方保密计算最值(最大值、最小值)问题是重要的安全多方计算问题,其解决方案具有重要理论价值和重要应用前景.然而,目前已存在的方案不多,而且方案效率不理想,不利于实际应用.因此,本文采用0-1 编码的方法,结合多密钥全同态加密算法,将最值问题架构在云计算平台之上进行解决,构造相应协议,并利用模拟范例的方法证明了协议的安全性.同已有的解决方案比较,本文方案不仅取得了较高的效率,还适合云计算平台,同时,本文方案采用了NTRU 加密算法,由于其安全性是与求解最坏情况格上困难问题是等同的,因此被认为可以抵抗量子攻击,所以本文协议也可以抵抗量子攻击,最后,将协议1 应用在统计学领域中,解决了多方保密计算极差问题. 本文方案都是在半诚实模型下构造的,只能防止半诚实敌手攻击,而实际应用中会遇到恶意敌手,尽管存在从半诚实协议到恶意模型协议的通用转化方法,然而针对多方保密计算最值问题,如何设计恶意模型下相应协议,具体问题需要寻找各种可能的恶意攻击方法,进而构造恶意模型下相应的协议,这将是未来研究的工作之一.


3.3 具体协议

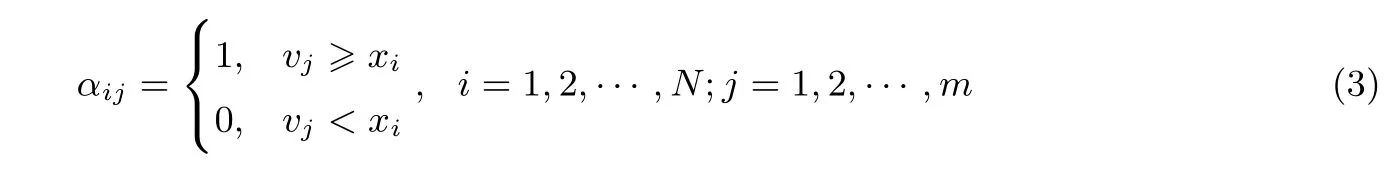


3.4 安全性分析
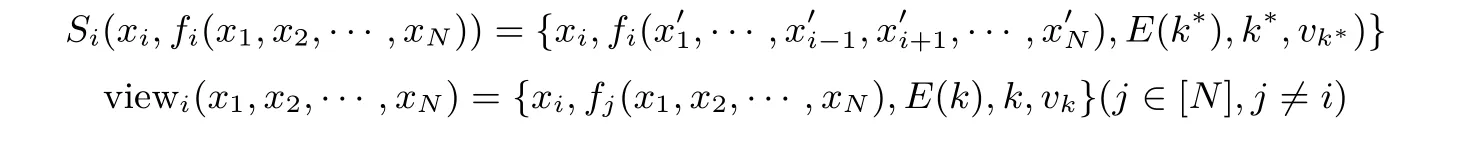

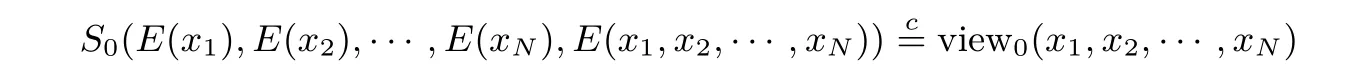
3.5 效率分析




4 最大值、最小协议在统计学上的简单应用—多方保密计算极差
4.1 问题描述
4.2 问题的转化
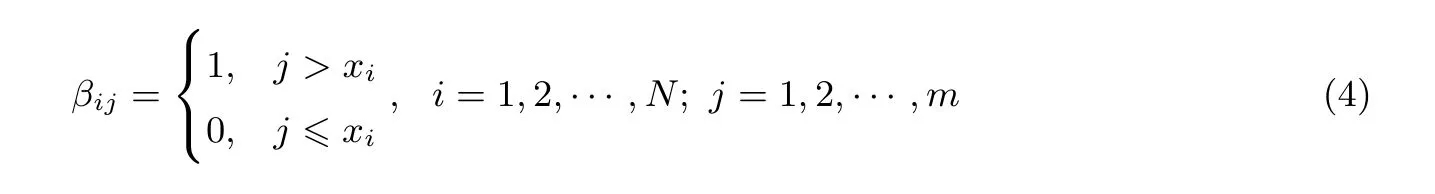


4.3 具体协议

5 总结与展望
