Piccolo算法的Biclique分析*
2019-06-10徐林宏郭建胜崔竞一李明明
徐林宏,郭建胜,崔竞一,李明明
信息工程大学,郑州 450001
1 引言
物联网的兴起带来了微型设备的大量应用,像智慧交通、智能物流等,给人们的生活带来了很大的方便,但终端资源非常有限,其中的安全问题是一个急需解决的问题,主要是未授权用户对数据的生成、访问和篡改,所以轻量级密码算法[1–3]和协议[4–6]就成了密码学术界关注的焦点.
Piccolo 算法是由日本密码学家Shibutani 等人[7]于CHES 2011 上提出的一种基于广义Feistel 结构设计的轻量级分组密码算法,适用于资源受限的环境,有较高的硬件实现效率.该算法分组规模为64 bits,根据密钥规模的不同,可分为Piccolo-80 和Piccolo-128 两类.
Biclique 分析方法由Bogdanov 等人[8]在AsiaCrypt 2011 上提出,是对分组密码以及Hash 函数的一种新型攻击方法,初始用于对全轮AES 算法进行攻击,并使得攻击复杂度低于穷举攻击.同样的,Biclique 对于其他的分组密码算法,尤其是轻量级分组密码算法这类具有简单密钥调度设计的算法也有较好的攻击效果,例如对CLEFIA[9]、LBlock[10]、PRESENT[11,12]、PRINCE[13]等算法的安全性分析.
现有的对于Piccolo 算法的安全性分析结果较多,其中,在单密钥条件下利用统计类的分析方法(差分、线性、积分分析等)以低于穷举复杂度对Piccolo 算法的最优攻击轮数[14]分别为Piccolo-80 算法14轮、Piccolo-128 算法18 轮.而基于Biclique 分析能够攻击全轮分组密码算法的特性,可对全轮的Piccolo算法进行安全性评估.在已有的对于Piccolo 算法的Biclique 攻击结果中,大多是通过构造平衡Biclique结构实施攻击.2012年,Wang 等人[15]最先给出了全轮Piccolo-80 算法和缩减轮的Piccolo-128 算法在不考虑白化密钥条件下的Biclique 分析结果;2013年,Jeong 等人[11]利用Biclique 分析方法给出了全轮PRESENT、Piccolo 和LED 算法的攻击结果;2017年,Han 等人[16]通过改进Jeong 等人的工作,降低了对全轮Piccolo 算法Biclique 攻击的复杂度;利用非平衡Biclique 结构对Piccolo 算法进行攻击体现在2014年Ahmadi 等人[17]的工作中.
本文主要使用非平衡Biclique 攻击的方法对Piccolo 算法进行安全性分析,利用文献[8,18]中构造Biclique 结构的方法,通过建立非平衡Biclique 结构以及Stars 结构,分别给出了Piccolo-80 和Piccolo-128 算法的非平衡Biclique 攻击和Stars 攻击结果,增加考虑存储方面的复杂度.与现有攻击结果相比,分别在数据复杂度和计算复杂度方面有所优化.本文攻击结果如表1 所示.
第1 节介绍本文研究背景,第2 节主要介绍Piccolo 算法和Biclique 攻击的相关知识,对Piccolo-80和Piccolo-128 算法的非平衡Biclique 分析和Stars 攻击主要在第3 节和第4 节中给出,第5 节总结全文.
2 相关知识
2.1 符号说明
:第r轮算法的第i个分块,i∈{0,1,···,7}
Pi:Biclique 结构明文状态
Ci:Biclique 结构密文状态
Sj:Biclique 结构中间状态
Vi,j:匹配向量位置
wkt:第t个白化密钥
(rk2r,rk2r+1):第r轮轮密钥
2.2 Piccolo 算法
Piccolo 算法采用广义Feistel 结构,其密钥规模有80 bits 和128 bits 两种,分组规模均为64 bits,从而可分为Piccolo-80 和Piccolo-128 两个版本,加密轮数分别为25 轮和31 轮.它的加密环节包括密钥白化、F函数和字节置换操作.密钥白化操作仅在第一轮和最后一轮存在,保证加脱密结构的一致性.轮变换主要由F函数和字节代替组成,下面具体介绍轮变换的各个环节和密钥扩展算法,完整的Piccolo 加密变换如图1 所示,其中r表示加密轮数.

表1 Piccolo算法的Biclique 分析结果对比Table 1 Comparison of Biclique analysis results of Piccolo

图1 Piccolo算法结构Figure 1 Structure of Piccolo
F 函数该变换对16 bits 数据进行操作,其主要由8 个相同的4 比特双射S 盒和一个列混合矩阵M组成,用来实现算法的混乱和扩散.列混合矩阵M的运算定义在由不可约多项式x4+x+1 生成的GF(24)上,具体形式如下.
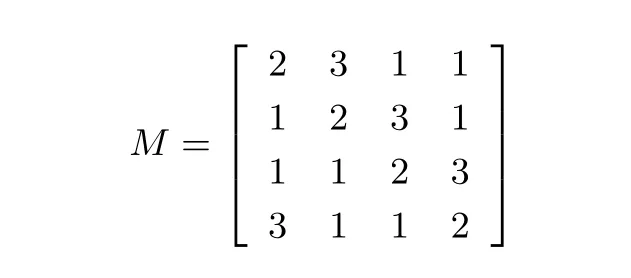
表2 给出了双射S 盒,图2 给出了F函数的具体构造.

表2 4比特双射S 盒Table 2 4 bits S-Box with bijection
轮置换RP初始将明文数据分成四部分,每部分由两个字节组成,也就是图1 中的P0到P3,则在进行轮置换时,以字节为单位进行置换操作.在本文中,为了便于攻击,根据F函数中的S 盒为4 比特,可将每一字节分割成两个半字节进行操作,即每一轮的输入状态表示为左右两个半字节具体如图3 所示.
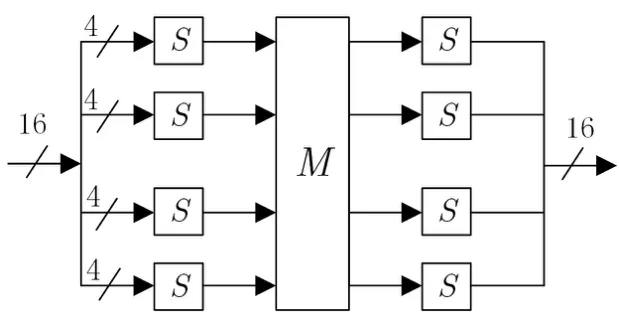
图2 F函数Figure 2 F function

图3 轮置换RPFigure 3 Round permutation
密钥扩展算法Piccolo 算法的密钥扩展根据密钥规模不同,同样分为80 bits 和128 bits 密钥两种.对于Piccolo-80,将80 bits 主密钥划分为5 个部分,每个部分包括两字节,即K=K0||K1||K2||K3||K4,其中,由于F函数中采用的是4 比特S 盒,因此,在这里,我们可以将主密钥继续作划分,对每一字节密钥再划分,即白化密钥wkj,j∈(0,1,2,3)由主密钥直接生成,也就轮密钥(rk2r,rk2r+1),r∈{0,···,24} 由主密钥与固定常数异或所得,具体对应关系见表3.对于Piccolo-128,与Piccolo-80 主要区别在于主密钥增加了6 个字节,得到K=K0||K1||K2||K3||K4||K5||K6||K7,相应的白化密钥也有所变化,即轮密钥r∈{0,···,30},具体对应关系见表4.Piccolo 算法的具体构造详见文献[7].
2.3 Biclique攻击方法介绍
Biclique 攻击本质上是基于中间相遇思想,借助算法密钥扩展的弱点给出密钥恢复方案的一种攻击方法.在文献[8]中,作者提出了两种构造Biclique 结构的方法,分别为独立Biclique 结构和长Biclique结构.由于独立Biclique 结构更易构造,所以后续的攻击一般采用此结构对密码算法进行Biclique 分析,本文中亦如此.2017年崔竞一等人[18]运用独立Biclique 结构提出了一种广义Biclique 自动攻击框架,在进行具体攻击时,根据构造所得结构维数不同,可分为平衡Biclique 攻击、Stars 攻击[19]和非平衡Biclique 攻击.本文基于文献[18]的分类方法,主要研究Piccolo 算法在非平衡Biclique 攻击和Stars 攻击下的安全性,有效利用预计算技术降低攻击所需计算复杂度.下面对一般情形下Biclique 结构的构造和攻击流程以及预计算匹配技术进行介绍.

表3 Piccolo-80 算法的主密钥与轮密钥之间的对应关系Table 3 Correspondence between master key and round key of Piccolo-80

表4 Piccolo-128 算法的主密钥与轮密钥之间的对应关系Table 4 Correspondence between master key and round key of Piccolo-128
2.3.1 Biclique结构构造
简单来说,一个Biclique 结构就是一个二分图,一般通过三元组的形式表示.令l轮子算法f在密钥K[i,j]作用下将密文状态C中的2d1个元素Ci映射到中间状态S中的2d2个元素Sj,也就是其中∀i∈{0,1,···,2d1−1},∀j∈{0,1,···,2d2−1}.将这样的三元组({Ci},{Sj},K[i,j])记为(d1,d2)维Biclique 结构.当d1=d2=d0 时,将其称为平衡Biclique 结构,当d1=0,d2=d0时称为Stars 结构,d1d2且均不为0 时为非平衡Biclique 结构.下面详细介绍非平衡Biclique 结构的构造方法,图4 为一般的Biclique 结构示意图.
基于文献[8]的方法,选择一个上述三元组(C0,S0,K[0,0])满足在此基础上,选取两组相关密钥差分和得到两条独立的差分路径∇j和∆i,构造得到一个映射关系,满足对于2d1 个元素Ci在密钥K[i,j]作用下映射到2d2个元素Sj,即S0⊕∇jC0⊕∆i.令Ci=C0⊕∆i,Sj=S0⊕∇j,K[i,j]=K[0,0]⊕⊕则三元组({Ci},{Sj},K[i,j])即所构造得到的一个Biclique 结构,其中i∈{0,1,···,2d1−1},j∈{0,1,···,2d2−1},当d1=d2=d0 时,则构造所得为一个平衡Biclique 结构.对于非平衡Biclique 结构的构造,可利用文献[18]的方法,将密钥差分相互独立的多个平衡Biclique 结构进行组合得到,如下文中3.1 节;也可以通过选取两组不平衡的密钥差分直接利用上述方法构造得到,如4.1 节.此外,在结构构造中,为了使得攻击效果更好,根据算法实际,还可选择有明文方向或密文方向两种构造方式.

图4 Biclique 结构示意图Figure 4 Biclique structure
2.3.2 Biclique 攻击流程
将一个分组密码e看成多个子算法的结合,即使得由密文状态C映射到明文状态P有如下表示:
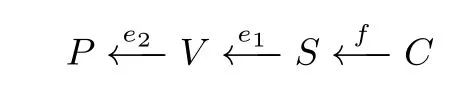
其中f表示构造Biclique 结构的子算法,进而可将Biclique 攻击分为以下四步.
1.密钥划分.敌手将分组密码e上的主密钥2n分割成不同的2n−d1−d2个密钥空间,每一个密钥空间内有2d1+d2个候选密钥K[i,j],i∈{0,1,···,2d1−1},j∈{0,1,···,2d2−1}.
2.构造Biclique 结构.敌手依据划分所得的每个密钥空间K[i,j],在子算法f上构造Biclique 结构.
3.匹配阶段.敌手通过子算法f上的Biclique 结构得到2d1个状态Ci,在正确密钥解密下得到对应的密文Pi,而后从Pi由子算法前向计算得到对应的2d1个匹配状态Vi,0,即相应的,从2d2个状态Sj后向计算得到2d2个匹配状态V0,j,即V0,j在此基础上,进行状态匹配,保留满足的K[i,j]作为正确的候选密钥予以保留,其余的筛除.
4.密钥筛选.对候选密钥集进行穷举,得到正确密钥.
这里仅以密文方向的Biclique 分析为例进行了介绍,明文方向的攻击过程与密文方向基本一致.攻击复杂度主要包括数据复杂度、存储复杂度和计算复杂度.数据复杂度由构造Biclique 结构所需的选择明(密)文数量决定,存储复杂度由构造得到的Biclique 结构的维度以及预计算过程中的非线性环节数量决定.计算复杂度主要包括三个部分,分别是Biclique 结构构造、状态匹配阶段以及密钥筛选阶段的计算复杂度,即C=CBiclique+Cmatch+Cfalse.
引理1(预计算匹配技术)[8]根据2.3.2 节中介绍的攻击中的状态匹配过程,攻击者通过检验前向和后向匹配过程得到的匹配向量值是否一致,筛选错误密钥.考虑可以发现,当固定i,对于两个不同的j,在前向匹配阶段,即中有部分状态值一直保持不变,因此我们在攻击时对这些部分仅需计算一次.同样的,在后向匹配阶段,固定j,对于密钥差分i和0,即V0,j和中那些状态值不变的部分仅需计算一次.基于此特点,在匹配阶段,选定匹配向量,预计算那些在不同的密钥差分条件下仍保持不变的状态值,并进行存储,只对状态值发生改变的部分进行重计算,再进行状态匹配,能够有效降低攻击所需计算复杂度.
3 Piccolo-80算法的Biclique分析
首先,给出Piccolo 算法的几点性质,有助于下一步实施Blicique 攻击.
性质1通过统计Piccolo-80 算法的密钥扩展算法中主密钥的每一Ki,i∈{0,1,···,5} 出现的次数可得,除白化密钥外,轮密钥中(K0,K1)与(K2,K3)组合出现的概率均为10 次,(K4,K4)出现的概率为5 次.进而想要使得攻击效果更好,在构造Biclique 结构时,应尽量选择在K4上进行密钥划分.同样的,对于Piccolo-128 算法的密钥扩展算法中的每一Ki,i∈{0,1,···,8},除白化密钥外,K0、K1出现的次数均为7 次,其余均为8 次.因此选择在这两个密钥位置进行密钥划分能使得攻击结果更优.
性质2[14]Piccolo 算法的非线性环节—F函数采用是SDS 结构,如图2 所示.由于对于单个F函数进行计算所需的复杂度远大于其他环节操作例如异或操作,因此,在本文的攻击中,计算复杂度均以所需计算的F函数的个数作为衡量指标.在状态匹配阶段,当F函数输入比特全部活动,输出比特仅有一半活动时,也就是需计算4 个输入S 盒和2 个输出S 盒,则所需的计算复杂度约为个F函数,同样的仅在输入有一半比特不活动,所需计算复杂度也为个F函数;仅在输入或输出一侧有比特活动时,另一侧比特全部活动时,所需计算复杂度约为个F函数.
下面依据上述性质,介绍对于Piccolo 算法的非平衡Biclique 攻击和Stars 攻击.
3.1 Piccolo-80算法的(4,8)非平衡Biclique分析
在该部分,利用文献[18]中构造Biclique 结构的方法,通过两个低维的(4,4)平衡Biclique 结构结合得到一个(4,8)非平衡Biclique 结构,并依此对Piccolo-80 算法进行了Biclique 分析.根据密钥扩展算法,为了得到更好的攻击效果,选择从密文方向进行Biclique 结构构造.
密钥划分借助性质1,选取为活动比特位,令K[0,0,0]为上述三个位置密钥为0,其余比特遍历的主密钥.划分80 bits 主密钥为268个集合,每一子密钥集合包含212个密钥K[i,j1,j2],(i,j1,j2∈{0,1}4).K[i,j1,j2]定义为由K[0,0,0]与三个密钥差分组成,其中
Biclique 结构构造首先依据划分的密钥空间,利用对应的轮密钥构造相关密钥差分路径∆i、∇j1、∇j2,如图5 所示.显然(∆i,∇j1)和(∆i,∇j2)中没有重合的F函数,因此构造得到了两个密文方向的6轮(4,4)平衡Biclique 结构.然后利用文献[18]中的构造方法,将这两个平衡Biclique 结构进行组合,就得到了一个6 轮(4,8)非平衡Biclique 结构({Sj1,j2},{Ci},K[i,j1,j2]).
状态匹配根据构造得到的一个6 轮(4,8)非平衡Biclique 结构,得到24个状态Ci,通过正确密钥解密得到对应的24个明文状态Pi.选择与文献[17]相同的匹配向量,即第10 轮的第6 个字节为匹配向量,也就是由Pi向下加密10 轮,定义为前向匹配过程,Sj1,j2向上解密9 轮,定义为后向匹配过程.结合引理1,在前向匹配时只需对图中2.75 个F函数进行预计算,2.25 个F函数进行24次重计算,11.25 个F函数进行28次重计算,即可完成匹配,如图6(c)所示.图6 中(a)表示前向匹配过程中使用K[i,j1,j2]和K[i,0,j2]进行加密时的差分活动情况,(b)表示前向匹配过程中使用K[i,j1,j2]和K[i,j1,0]进行加密时的差分活动情况,(c)表示两者结合,在前向匹配过程中需要重计算的活动比特情况.(d)表示后向匹配过程中重计算的活动比特情况.后向匹配过程需要对图中2.75 个F函数进行预计算,13.5 个F函数进行24次重计算即可完成匹配.图6 中黑色标识需28次重计算的活动比特块,灰色标识需24次重计算的活动比特块,白色表示非活动比特块,下文中的图中标识均与此相同.

图6 Piccolo-80 算法的非平衡Biclique 攻击匹配阶段Figure 6 Matching phase of unbalanced Biclique attack for Piccolo-80
密钥筛选由于使用的匹配向量共28个可能值,因此平均一个错误密钥通过筛选的概率为2−8.又由每个密钥子集合中含有212个密钥,所以每个密钥子集合平均有212×2−8=24个密钥通过筛选,即得到了24个候选密钥.最后,每次攻击均对剩余的24个候选密钥进行全轮加密,检验得到初始的正确密钥.定理1 给出了上述Piccolo-80 算法非平衡Biclique 攻击所需的复杂度.
定理1利用6 轮(4,8)非平衡Biclique 结构对Piccolo-80 算法进行攻击,可恢复全轮Piccolo-80 算法的主密钥,其数据复杂度为236,存储复杂度为211.12,计算复杂度为279.03.
证明:数据复杂度主要由构造Biclique 结构所需的明密文量决定,由图5 可得,对每一个Biclique结构,需要固定密文C0,,差分不活动,其余位置遍历所有可能值,因此攻击所需的数据复杂度为236个选择密文.
存储复杂度由存储Biclique 结构以及利用预计算匹配技术,存储预计算的F函数这两部分构成.对于Biclique 结构的存储,实际上就是对密文状态和中间状态之间的对应关系进行存储,也就是需要顺序存储24个密文和28个中间状态的对应关系,每个状态为8 字节,共需存储(24+28)×8 字节.另外,由于在匹配阶段使用了预计算匹配技术,需要对攻击中不受活动比特影响的F函数进行预计算并存储,共有2.75+2.75 个F函数,每个F函数状态均为8 字节,因此需要存储(2.75+2.75)×8 个字节.综上,上述攻击所需存储复杂度为211.12个字节.
攻击所需的计算复杂度主要由三部分构成.一是构造Biclique 结构所需的复杂度,本节中利用文献[18]的非平衡Biclique 结构构造方法,能够有效降低结构构造所需的计算复杂度.由图5 可知,构造过程所需的计算复杂度约为
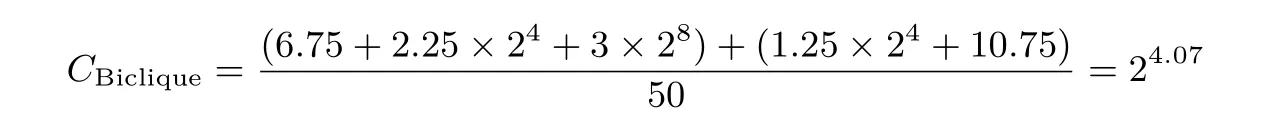
次全轮Piccolo-80 加密.二是匹配阶段的计算复杂度,主要包含前向匹配和后向匹配两个部分.根据上述攻击过程可得,前向匹配阶段需2.75 个F函数进行预计算,2.25 个F函数进行24次重计算,11.25个F函数进行28次重计算,后向匹配需要对2.75 个F函数进行预计算,13.5 个F函数进行24次重计算.即匹配阶段所需的计算复杂度总计为:Cmatch=29.87+210.13≈211.01次全轮Piccolo-80 加密.三是密钥筛选阶段的计算复杂度,由每一密钥子集合剩余24候选密钥,则Cfalse=24.因此上述攻击所需的计算复杂度总计为C=268×(24.07+211.01+24)≈279.03次全轮Piccolo-80 加密.
综上,对于Piccolo-80 算法的(4,8)非平衡Biclique 攻击所需的数据复杂度为236个选择密文,存储复杂度为211.12个字节,计算复杂度为279.03次全轮Piccolo-80 加密.
3.2 Piccolo-80算法的Stars攻击
Stars 攻击是由Bogdanov 等人[19]在ICISC 2014 上提出的一种Biclique 攻击方法,最先用于AES算法.其本质上与非平衡Biclique 攻击相似,攻击过程也基本一致,但所需数据复杂度很少,一般为2–3个已知明文,相应的攻击所需计算复杂度就有所增加.本小节中就运用此方法对Piccolo-80 算法进行了安全性分析,给出了对于Piccolo-80 算法最低数据复杂度的攻击结果.
密钥划分选取()为活动比特位,划分80 bits 主密钥为272个集合,每一子密钥集合包含28个密钥K[i,j],(i,j ∈{0,1}4).
Stars 结构构造首先依据划分的密钥空间,利用对应的轮密钥构造相关密钥差分路径∆i、∇j,该两条差分中没有重合的F函数,因此构造得到了一个明文方向的4 轮8 维的Stars 结构.具体结构见图7.

图7 Piccolo-80 算法的4 轮8 维Stars 结构Figure 7 4 rounds of 8-dimensional Stars structure of Piccolo-80
状态匹配与3.1 节介绍的状态匹配过程类似,根据构造得到的8 维Stars 结构,在第10 轮进行匹配,选取匹配向量的位置为.由图8 可得,前向匹配中需对2.75 个F函数进行预计算,2.25 个F函数进行24次重计算,11.25 个F函数进行28次重计算,后向匹配中完成匹配需要对1 个F函数进行24次重计算,19.25 个F函数进行28次重计算.

图8 Piccolo-80 算法的Stars 攻击匹配阶段Figure 8 Matching phase of Stars attack for Piccolo-80
密钥筛选由于使用的匹配向量共28个可能值,因此平均一个错误密钥通过筛选的概率为2−8.又由每个密钥子集合中含有28个密钥,则平均得到了1 个候选密钥.最后,对每一密钥子集合进行一次全轮加密,检验得到初始的正确密钥.对于Piccolo-80 算法的Stars 攻击所需复杂度由定理2 给出.
定理2利用4 轮8 维Stars 结构对Piccolo-80 算法进行攻击,能够以最低的数据复杂度恢复出主密钥,其数据复杂度为2,存储复杂度为28.12,计算复杂度为279.31.
证明:存储复杂度包括Stars 结构以及预计算的F函数这两部分.对于Stars 结构,共需存储(24+24)×8=28个字节,F函数需存储2.75×8 个字节,即上述攻击所需存储复杂度为28.12个字节.
攻击所需的计算复杂度包括构造Stars 结构、攻击匹配阶段以及密钥筛选阶段三部分.其中,结构构造所需的计算复杂度为CStars=匹配阶段所需的计算复杂度总计为Cmatch=次全轮Piccolo-80 加密,密钥筛选阶段的计算复杂度为Cfalse=1.因此上述攻击所需的计算复杂度总计为C=272×(2−0.9+27.30+1)≈279.31次全轮Piccolo-80 加密.数据复杂度方面,使用2 个明密文对,使得攻击成功率为1.
4 Piccolo-128算法的Biclique分析
本节中主要介绍对Piccolo-128 算法的非平衡Biclique 攻击和Stars 攻击.在进行非平衡Biclique攻击时,由于Piccolo-128 算法的密钥扩展方式的约束,我们不采用第3 节中Biclique 结构的构造方法,而是通过选取特定的密钥差分,基于文献[8]的方法直接构造(4,8)非平衡Biclique 结构.虽然使得构造结构所需的计算复杂度增加,但相应的降低了匹配阶段的计算复杂度,使得整体攻击所需复杂度有所优化.下面对具体攻击进行介绍.
4.1 Piccolo-128算法的(4,8)非平衡Biclique分析
基于密钥扩展算法的影响,我们从明文方向直接构造Biclique 结构,攻击步骤与第3.1 节对Piccolo-80算法的攻击相同.
密钥划分选取()为活动比特位,令K[0,0]为上述两个位置密钥为0,其余比特遍历的主密钥.划分128 bits 主密钥为2116个集合,每一子密钥集合包含212个密钥K[i,j](i∈{0,1}4,j∈{0,1}8).K[i,j]定义为由K[0,0]与两个密钥差分、组成,其中
Biclique 结构构造基于划分的密钥空间,利用对应的轮密钥构造相关密钥差分路径∆i、∇j,显然(∆i,∇j)中没有重合的活动F函数,因此构造得到了一个明文方向的5 轮(4,8)非平衡Biclique 结构({Pi},{Sj},K[i,j]),i∈{0,1}4,j∈{0,1}8.具体结构详见图9(a).
状态匹配基于上述构造得到的一个5 轮(4,8)非平衡Biclique 结构,得到24个状态Pi,在选择明文条件下,得到对应的24个密文状态Ci.选择第17 轮的第6 个字节的左半部分为匹配向量,即,前向匹配过程为由Sj向下加密12 轮,后向匹配过程Ci向上解密9 轮.结合引理1,在前向匹配时只需对图中5.875 个F函数进行预计算,14.375 个F函数进行24次重计算,即可完成匹配,完成后向匹配需要对图中9.75 个F函数进行预计算,16.5 个F函数进行28次重计算.匹配过程如图9(b)所示.
密钥筛选由于使用的匹配向量共28个可能值,因此平均一个错误密钥通过筛选的概率为2−8,即得到了24个候选密钥.最后,每次攻击均对剩余的24个候选密钥进行全轮加密,检验得到初始的正确密钥.上述对于Piccolo-128 算法非平衡Biclique 攻击所需的复杂度由定理3 给出.
定理3基于5 轮(4,8)非平衡Biclique 结构对Piccolo-128 算法进行攻击,可恢复全轮Piccolo-128算法的主密钥,其数据复杂度为220,存储复杂度为211.17,计算复杂度为2127.05.
证明:由图9 可得,对每一个Biclique 结构,需要固定明文(P0,P1,,)差分不活动,其余位置遍历所有可能值,因此攻击所需的数据复杂度为220个选择明文.攻击中需顺序存储24个明文和28个中间状态的对应关系以及匹配阶段预计算的(5.875+9.75)个F函数,因此存储复杂度为(24+28+5.875+9.75)×8 ≈211.17个字节.计算复杂度方面,在Biclique 结构构造时,需要预计算10 个F函数,0.625 个F函数进行24次重计算,8.25 个F函数进行28次重计算,即次全轮Piccolo-128 加密.匹配阶段的计算复杂度为29.93+210.10≈211.01,又由Cfalse=24,因此,计算复杂度总计为C=2116×(25.10+211.01+24)≈2127.05次全轮Piccolo-128 加密.
4.2 Piccolo-128算法的Stars攻击
该部分的攻击过程与Piccolo-80 算法的Stars 攻击相似,这里就进行简要介绍.
密钥划分利用性质1,选取()为活动比特位,划分128 bits 主密钥为2120个集合,每一子密钥集合包含28个密钥K[i,j],(i,j∈{0,1}4).
Stars 结构构造首先依据划分的密钥空间,利用对应的轮密钥构造相关密钥差分路径∆i、∇j,该两条差分中没有重合的F函数,因此构造得到了一个明文方向的4 轮8 维的Stars 结构.
状态匹配根据构造得到的8 维Stars 结构,在第16 轮进行匹配,选取匹配向量的位置为.则前向匹配过程中需对1 个F函数进行24次重计算,19.25 个F函数进行28次重计算,后向匹配中完成匹配需要对4.75 个F函数进行预计算,2.25 个F函数进行24次重计算,21.25 个F函数进行28次重计算.
密钥筛选由于使用的匹配向量共28个可能值,因此平均一个错误密钥通过筛选的概率为2−8.因此可平均得到了1 个候选密钥.最后,对每一密钥子集合进行一次全轮加密,检验得到初始的正确密钥.

图9 Piccolo-128算法的非平衡Biclique 结构和攻击匹配阶段Figure 9 Structure and matching phase of unbalanced Biclique attack for Piccolo-128
Piccolo-128 算法的Stars 攻击结构和匹配过程见图10,图10 中(a)表示4 轮8 维Stars 结构,(b)表示Stars 攻击状态匹配过程.定理4 给出了该攻击的各类指标,证明过程与定理2 类似.
定理4利用4 轮8 维Stars 结构对Piccolo-128 算法进行攻击,能够以最低数据复杂度恢复主密钥,其数据复杂度为2,存储复杂度为28.19,计算复杂度为2127.40.

图10 Piccolo-128 算法的Stars 攻击结构和匹配阶段示意图Figure 10 Structure and matching phase of Stars attack for Piccolo-128
5 结束语
本文利用Biclique 攻击方法对Piccolo 算法在非平衡Biclique 攻击和Stars 攻击下的安全性进行了评估,结合Piccolo-80 与Piccolo-128 算法的密钥扩展的相关性质,分别给出了目前对于该两种算法最低数据复杂度和最优计算复杂度的Biclique 攻击结果.分析表明,对于同一分组密码算法,使用非平衡Biclique 攻击方法所需的计算复杂度较平衡Biclique 攻击更低,使用Stars 攻击方法能够以最低的数据复杂度恢复出算法主密钥.而这三类Biclique 攻击之所以均能以低于穷举攻击的复杂度实现,主要在于密码算法具有简单的密钥扩展,并且算法本身扩散性弱,存在多条独立的差分路径,从而能够有效降低攻击复杂度.
根据轻量级密码算法扩散性强弱的不同,利用多种Biclique 攻击方法所得的攻击效果也不同,因此能否利用本文的方法,对更多的轻量级分组密码算法,特别是SPN 结构类、ARX 结构类等算法有较好的攻击效果是下一步研究的方向.
