直方图与饼形图的保密生成协议*
2019-06-10王颖囡窦家维
葛 雪,王颖囡,窦家维
陕西师范大学数学与信息科学学院,西安 710119
1 引言
网络的迅速发展为多个参与者利用各自的保密数据联合进行数据挖掘、知识发现、信息搜索以及寻求数据之间的各种统计规律、合作进行科学研究等提供了巨大的机会,同时也给参与者的信息安全带来了巨大的挑战.在互不信任的网络环境中,参与者需要保护各自所拥有数据的隐私,在联合计算过程中稍有不慎就可能导致数据的机密性丧失与隐私泄露.运用安全多方计算技术,既能充分发挥机密数据的作用,又能保护数据的机密性与隐私,这使得安全多方计算越来越受到人们的关注.
1982年姚期智[1]提出了两个参与者的安全计算问题,1988年Ben 和Goldwasser[2]引入了多个参与者的安全多方计算问题.安全多方计算是指两个或更多参与者利用各自的保密数据,联合进行的保密计算.计算结束后,没有参与方能够获得多于规定输出的信息.安全多方计算是网络空间信息安全与隐私保护的关键技术,它对于计算科学、密码学和信息安全的理论与实践都有重要的意义,是国际密码学界近年来的研究热点[3–5].Goldwasser[6]预言具有丰富理论基础和广泛应用前景的安全多方计算将成为计算科学一个必不可少的工具.Cramer[7]也指出安全多方计算将成为计算科学一个威力强大的工具.
Yao、Goldwasser 以及Goldreich 等人[8–10]奠定了安全多方计算的理论基础.他们证明了所有安全多方计算问题都是可解的,并给出了解决方案.但是他们指出这些解决方案存在的共同问题是它们的效率都太低了,利用这些通用的解决方案去解决现实生活中各种各样的问题是不切实际的.因此对具体问题应该设计具体的解决方案.
在Goldwasser,Goldreich 和Cramer 关于安全多方计算研究与论述的激励下,人们研究了各种各样的安全多方计算问题,如保密的科学计算[1,11–17]、保密的计算几何[18–20]、保密的统计分析[21,22]、保密的数据挖掘[23–25]、其他安全多方计算的应用[26,27]等,但仍有许多问题需要研究.
其中,保密的统计分析是研究如何在合作环境下进行统计分析,并确保每个参与者自身数据的安全性,这在自然科学、工程技术、社会科学的各个方面都有非常广泛的应用.本文主要研究了保密生成直方图、饼形图的问题,这是保密的统计分析中一个非常重要的问题.就目前我们所知,还没有见到关于这个问题的解决方案.直方图与饼形图是一种统计报告图,二者的优点是可以直观地看出数据整体的分布情况.与数据的排序相比,直方图与饼形图更加直观,在数据较多时,对数据进行一一进行排序是不太现实的,会耗费过多的人力物力而收益甚微.在实际生活中,直方图、饼形图有非常多的应用场景,比如:一个学校想要知道学生成绩的分布情况,但是每个班的成绩、每个同学的成绩都属于个人隐私,同学们不想对外公布,这时候就涉及到保密求直方图、饼形图的问题.另外,对于各地区隐私疾病直方图、保密投票数据的直方图与饼形图等等在现实生活中都十分常见,因此研究直方图与饼形图的保密生成问题是十分必要的.
本文的主要贡献如下:
(1)提供了一种新的编码方法,能够将参与者的保密数据隐藏在数组中.
(2)利用该编码方法结合Paillier 加法同态加密算法,设计了第一种保密生成直方图的解决方案.该方案可以抵抗P1不参与时的合谋攻击.
(3)利用该编码方法结合椭圆曲线加法同态加密算法以及门限加密算法,设计了第二种保密生成直方图的解决方案.第二种方案可以抵抗任意数量的合谋攻击,并且效率也提高许多.
2 预备知识
2.1 安全性定义
半诚实模型:所谓半诚实参与者[10]是指那些在协议的执行过程中按照协议要求忠实地履行协议的参与者,但他们可能会记录下协议执行过程中收集到的所有信息,在协议执行后试图根据记录的信息推算出其他参与者的输入.如果所有的参与者均为半诚实参与者,这样的计算模型称为半诚实模型.由于半诚实参与者不对协议实施主动攻击,所以半诚实模型又称为诚实但好奇(honest-but-curious)模型或被动模型.
设有n个参与者P1,···,Pn,分别具有保密数据x1,···,xn,记X=(x1,···,xn).他们利用协议Π保密地计算f(X)=(f1(X),···,fn(X)),其中fi(X)(i∈[n]={1,···,n})为参与者Pi得到的输出结果.在协议执行过程中,Pi得到的信息序列记为

其中,ri表示Pi在协议中产生的随机数,(j=1,···,t)表示Pi收到的第j个信息.对于部分参与者构成的子集I={Pi1,···,Pis}⊆{P1,···,Pn},记
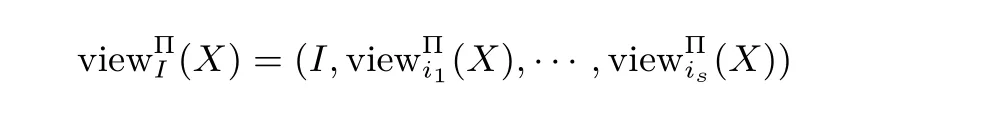
定义1(半诚实参与者的安全性[10])在参与者都是半诚实的情况下,如果存在概率多项式时间算法S,使得对于任意的I={Pi1,···,Pis}⊆{P1,···,Pn},均有下式成立:
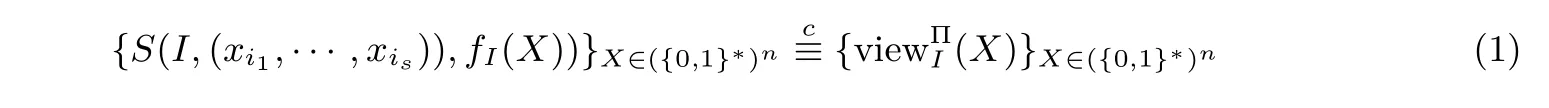
其中表示计算上不可区分,则称协议Π 保密地计算了n元函数f(X).
显然,如果对于任意n−1 个参与者构成的集合Γ,都存在满足(1)式的S,则协议Π 能够抵抗任意的合谋攻击.
2.2 Paillier同态加密算法
同态加密的概念在文献[28]中被首次提出,它可以保证在不影响明文数据机密性的情况下,直接操作密文来完成对明文的计算.简单来说,对密文的计算等价于明文计算之后再加密.
Paillier 方案[29]的具体过程如下.
密钥生成给定一个安全参数k,选择两个素数p,q,使得|p| =|q| =k,其中N=p×q,λ=lcm(p−1,q−1)是p−1 和q−1 的最小公倍数.随机选择一个g∈,使得gcd(L(gλmodN2),N)=1,定义为L(x)=.算法的公钥为(g,N),私钥为λ.
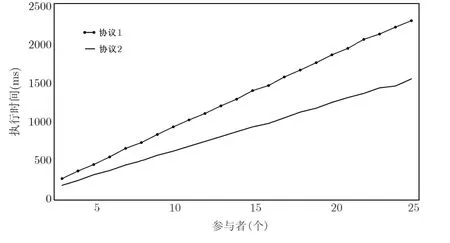
加密随机选择一个随机数r,r 解密计算 该算法是概率加密算法,具有加法同态性.假设密文为 那么 因此该算法满足如下性质: 椭圆曲线密码体制ECC(elliptic curve cryptography)是1985年由Miller 和Koblitz 共同提出的.其理论基础是定义在有限域上的某一椭圆曲线上的整数点与无穷远点可构成有限交换群.如果该群的阶包含一个较大的素因子,则其上的离散对数问题是困难的.与RSA 算法相比,ECC 具有计算量小、密钥短、对带宽和处理器要求低等优点.基于椭圆曲线实现ElGamal 密码体制[30]描述如下. 在使用椭圆曲线密码体制之前,必须设计把信息编码到椭圆曲线上的点的编码方法,具体如下[31]. (1)选择一个具有n个点的椭圆曲线. (2)选择一个辅助基本参数k,比如设k=20(加密解密双方达成一致). (3)对于每一个m,Fori=1 tok−1,令x=mk+i,利用椭圆曲线方程求y.如果找到就停止,如果找不到就令i←i+1,继续找,直到找到为止.实际上,可以找到一点(x,y),这个点就是消息m的编码. (4)解码:点(x,y)解码为的值向下取整). 密钥生成选定一条椭圆曲线EC(a,b)与其上的一个基点G,在上任意选择一个随机数h,计算H=hG.(H,G)就是公钥,h是私钥. 加密消息编码到EC(a,b)上一点M,并产生一个随机整数r,计算密文 解密对密文1,C2,用私钥h解密得到明文为 该算法是概率加密算法,具有加法同态性.假设密文 那么 因此该算法满足如下性质: 门限解密[32,33]是安全多方计算中对抗合谋攻击的一个重要工具.在门限解密密码体系中,n个参与者共同生成一个公钥,每个人持有一部分解密密钥.在加密过程中可以直接使用共同拥有的公钥加密消息,但是需要多个参与者共同合作才能对密文进行解密.如果解密一个消息至少需要t个人合作才能解密,少于t个人合作时将不能得到解密消息,这种密码体制被称为(t,n)门限密码体制. 本文需要抵抗尽可能多的合谋攻击,所以需要的是(n,n)门限密码系统用于抵抗n−1 个参与者的合谋攻击,这里可以利用椭圆曲线密码系统构造门限密码系统,具体构造如下. 密钥生成选定一条椭圆曲线EC(a,b)与其上的一个基点G,每个参与者Pi在上任意选择一个私钥hi,计算Hi=hiG,共同生成公钥 加密消息编码到EC(a,b)上一点M,并在上任意选择一个随机数r:1rn−1,计算密文C1,C2=m+rH,rG. 解密对密文C1,C2,通过下面解密过程得到明文: 问题描述:假设现有n个参与者Pi(i=1,2,···,n),每一个Pi都有多个数据记为ei={ei1,ei2,···},他们希望合作计算这些数据的直方图,同时不泄露其他任何私有信息(即参与方最后仅知道这些数据所生成的直方图与饼形图,并不知道其它参与者拥有的具体数据). 编码方法:首先每一个参与者Pi共同商定将区间分割为m份,记为 {[y1,y2),[y2,y3),···,[ym,ym+1]} ={S1,S2,···,Sm},其中Si=[yi,yi+1)(i=1,2,···,m−1),Sm=[ym,ym+1],接着按照下面的方法构造数组: 其中对于i∈{1,2,···,n},k∈{1,2,···,m}, 以此方式,每个参与者的数据ei与数组Xi一一对应.对此得到的n个数组X1,X2,···,Xn求和,即将这些数组对应元素相加,得到一个新的数组: 数组T即为所求对应区间所含元素的个数.根据区间{[y1,y2),[y2,y3),···,[ym,ym+1]} 以及数组T可绘制出相应直方图,对数组T稍加运算,计算出每个区间Si(i=1,2,···,n)所含元素个数占总数量的百分比,就可绘制出该数据的饼形图.下面以某个年级学生的数学成绩为例. 例1若将学生成绩分为[0,10),[10,20),···,[90,100]这10 个区间段,绘制表1. 表1 某个年级学生的数学成绩Table 1 Math scores of a grade 按照上述编码方式, 计算向量对应分量之和即为 则可得出对应的直方图,再稍加运算,可得到饼形图(如图1). 图1 某个年级学生数学成绩直方图与饼形图Figure 1 Histogram and pie charts of math scores of a grade 以上的编码方法就是本文计算直方图与饼形图的基本原理.直接这样计算是无法保密的,而在密文的条件下进行这样的操作就可以实现保密运算.本文用Paillier 加密算法与椭圆曲线门限加密对数组中的0和1 进行加密,使得任何参与者都无法分辨出数组中0 与1 的个数(由于求出直方图便可求出相应的饼形图,为叙述简洁,以下协议均仅求出直方图). 首先,应用具有加法同态性质的Paillier 加密算法给出一种保密生成直方图的基本方案,如协议1. 协议1直方图的保密生成协议. 输入Pi各自拥有的保密数据ei. 输出该组数据的直方图. (1)P1应用Paillier 公钥系统生成私钥sk 和公钥pk,并公布公钥pk. (2)每个参与者Pi(i=1,2,···,n)以公式(2)将自己的数据转化成数组Xi=(xi1,xi2,···,xim). (3)每个参与者Pi(i=1,2,···,n)用公钥pk 加密数组Xi得到E(Xi)=(E(xi1),E(xi2),···,E(xim)). (4)参与者Pi(i=1,2,···,n)计算如下(此处的向量相乘为E(Xi)和E(Xi+1)中对应分量相乘): (5)参与者Pn将E(Xn)发送给P1,P1计算X=Dec(E(Xn)),绘制相应的直方图并公布. 正确性分析在协议1 中,由于Paillier 加密算法的加法同态性(即对密文做乘法运算等于对相应的明文做加法运算后再加密),可得出: 安全性分析由于只有P1有私钥可以解密,所以协议可以抵抗没有P1参加的任何合谋攻击,但该协议不能抵抗有P1参与时的合谋攻击.以下是关于协议1 安全性的具体分析. 定理1直方图的保密生成协议在半诚实模型下是安全的. 证明:通过构造满足式(1)的模拟器S来证明本定理,此处选用可能参与合谋的最大合谋结构进行模拟.分为以下三种情况: (1)P1不参与合谋,P2,···,Pn合谋能获得P1的保密数据的信息. 因为只有P1才能够解密密文,如果他不参与合谋,除了P2,···,Pn的数据和他们生成的密文之外,P2,···,Pn收到的关于e1的信息只有E(X1)=(E(x11),E(x12),···,E(x1m))=(c11,c12,···,c1m).由于加密算法是语义安全的,(ci1,ci2,···,cim)和m个随机数是计算不可区分的.在此情况下, 给定输入(I,(e1,···,en),fI(X)),S随机选择使得f(X′)=fI(,···,en)=(···,)=fI(X)=f(e1,···,en)=(t1,t2,···,tm)用···,en进行模拟.首先按照协议要求构造数组=(,,···,),加密得到 模拟器S 按照协议要求进行加密运算.解密最终数组E(X′)得到 令S(I,(e1,···,en),fI(X))={I,e2,E(X2),···,en,E(Xn),fI(X′)},因为概率加密方案是语义安全的,所以E(X1)(),且fI(X1)c≡fI(),其他所有参数都是相等的,故 因此对于e1是安全的. (2)P1不参与合谋,P2,···,Pn的n−2 个合谋想得到其中一个的保密数据,因为这时P2,···,Pn的地位是平等的,能力是相同的,不失一般性假设P3,···,Pn合谋要获得P2的保密数据的信息.这种情况与第一种情况相同,用类似的模拟可以证明对于e2是安全的. (3)P1参与合谋.这种情况下的最大合谋结构仍然是包含P1的n−1 个参与者合谋,要得到某一个Pi∈{P2,···,Pn} 的某个参与者的保密数据ei所在的区间范围,无法知道ei的大小. 综上所述,该协议对于半诚实参与者是安全的. 在本文协议1 中,参与者Pi将E(Xi)先发送给Pi+1,Pi+1计算E(Xi)×E(Xi+1),并将其发送给下一个参与者,以此类推,直到Pn将最后的每个参与者加密向量对应分量的乘积E(Xn)发送给P1.P1将E(Xn)解密并公布,如果P1参与合谋攻击,比如,参与者P1和P3合谋,会恢复出P2的数据.所以需要借助门限椭圆曲线加密系统设计一个更安全、更高效的协议,以达到抵抗合谋攻击的目的.基本原理与上述相同,不再赘述. 协议2基于门限密码系统的直方图的保密生成方案. 输入Pi各自拥有的保密数据ei. 输出该组数据的直方图. (1)n个参与者P1,···,Pn首先选定一条椭圆曲线EC(a,b),G为其上基点.每个参与者分别选择一个私钥hi,计算Hi=hiG,共同生成公钥 将公钥H公开,私钥hi各自保留. (2)每个参与者P1,···,Pn分别做如下运算: (a)Pi将自己拥有的数据ei按公式(2)编码方式转化成数组Xi=(xi1,xi2,···,xim). (b)参与者Pi将数组Xi编码到EC(a,b)上作为椭圆曲线上的点Mi=(Mi1,Mi2,···,Mim). (c)Pi在上任意选择一个随机数rij:1rijn−1,计算密文 并公布. (3)参与者P1,···,Pn将加密后的数据E(Mi)依次相加(即对应分量相加),并记 (4)参与者Pi计算hiC2j(j=1,2,···,m),并公布.P1,···,Pn将其依次相加将得到 (5)最后参与者Pi只需计算 并绘制相应的直方图即可. 正确性分析在协议2 中,由于椭圆曲线密码体制具有加法同态性质(即对密文做加法运算等于对相应的明文做加法运算后再加密),可得出: 所以协议2 是正确的,可以求出数组T,并绘制相应的直方图. 安全性分析协议的安全性是基于椭圆曲线加密体制的安全性.由于门限椭圆曲线的公钥是由所有参与者共同产生的,即其中hi是参与者Pi所持有的私钥碎片,如果想解密的话,就必须拥有全部参与者的私钥碎片.所以整个解密的过程都必须要全部参与者参与,因而可以抵抗合谋攻击. 在计算过程中,每个参与者Pi对外仅公布了加密信息E(Mi),在解密过程中对外也仅公布了加密信息hiC2j(j=1,2,···,m),由椭圆曲线密码体制的安全性可知,在协议解密过程中如果Pi没有参与,将无法解密得到Mj.因此在解密过程中,Pi的数据是完全保密的.我们给出下面的定理,仅给出证明思路,详细的证明过程省略. 定理2在半诚实模型下,基于门限密码系统的直方图的保密生成协议2 是安全的. 证明:证明协议的安全性需要构造满足式(1)的模拟器S.根据语义安全的同态加密算法的性质,如果没有私钥,应用概率公钥系统加密的任何信息都是计算不可区分的,因此只要有一个参与者不合谋,对其他合谋者来说,他们实际执行协议时获得的view 和用满足生成直方图不变的任意一组输入进行模拟所得到的信息序列是计算不可区分的,所以只要在(1)式中令S(I,(xi1,···,xis)),fI(X))为模拟过程中的view,即可使(1)式满足. 本部分对上述两个保密生成直方图的协议效率进行分析比较.本文方案都是用同态加密算法解决直方图问题,基本运算都是模乘运算.(忽略各协议中所需要的乘法运算)用Paillier 加密系统加密或者解密一次需要进行两次模指数运算.应用椭圆曲线加密系统进行的是模加运算,模加运算的次数与加密过程中所选随机数r的二进制位数有关. 在本文协议1 中,每个参与者都需要对编码后的数组元素进行加密,n个参与者需要进行2mn次模指数运算,所以协议1 在加密过程中需要进行2mn次模指数运算.最后P1对E(Xn)进行解密,需要2m次模指数运算.所以协议1 共需要2m(n+1)次模指数运算,计算复杂性为2m(n+1). 在本文协议2 中,参与者都需要对编码后的数组元素进行加密,所以协议2 共加密2nm次.参与者利用自己的私钥对密文联合解密,共解密n次.加密和解密过程均需要进行模加运算,所以协议2 的计算复杂性是O(nlogr)模加运算(r表示加密过程中的随机数且0rp−1). 衡量通信复杂度的指标一般用协议交换信息的比特数,或者用通信轮数.在安全多方计算研究中通常用轮数. 在协议1 中,每个参与者需要将加密后的密文发送给Pn,Pn将收到的密文做运算后发送给P1解密,在这个过程中需要n轮通信.最后P1解密,并且将解密结果告诉Pi,需要n−1 轮通信.所以协议1 共需要2n−1 轮通信,通信复杂性为O(n). 在协议2 中,所有参与者构造公钥需要n−1 轮通信,加密过程宣布Mi,需要1 轮通信,解密过程宣布需要1 次通信,所以协议2 共需要n+1 轮通信,通信复杂性为O(n). 表2 协议性能比较Table 2 Protocol performance comparison 本节我们通过模拟实验来测试执行协议1、协议2 所用的时间,通过协议执行的时间来验证方案的效率执行情况. 实验测试环境:Windows 10 64 位操作系统,Intel(R)Core(TM)i5-6600 处理器CPU @3.30 GHz,8.00 GB 内存,用java 语言在MyEclipse 上运行实现.本文所做模拟实验均在此环境下进行. 实验方法:本实验中,我们的底层协议(Paillier 算法,椭圆曲线加密算法)是使用了现成的开源包.实验设定m=10,参与者数分别为n=3,4,···,25.为使数据准确,对n的每个设定值进行1000 次模拟实验测试,统计协议执行时间的平均值(忽略协议中的预处理时间).图2 描述了协议的执行时间随参与者个数增长的变化规律. 图2 协议的执行时间随参与者个数增长的变化规律Figure 2 Execution time of agreement varies with growth of number of participants 由图2 可知协议的执行时间随参与者个数增长而线性增加,并且很容易得出,基于椭圆门限解密的保密直方图生成方案效率要高于基于Paillier 加密算法的保密直方图生成方案. 本文设计了一种新的编码方法,以新的编码方法与同态加密算法为基础,分别利用Paillier 加法同态加密算法、门限椭圆曲线加法同态加密算法构造了保密生成直方图问题的两个安全多方计算协议.第一个协议在半诚实模型下是安全的,但不能有效地抵抗合谋攻击.第二个协议可以抵抗多达n−1 个参与者的合谋攻击.将协议加以推广可以适用于更加普遍的情形,今后将在现有的研究基础上进一步研究抗恶意参与者(主动攻击者)的直方图问题.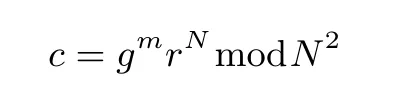
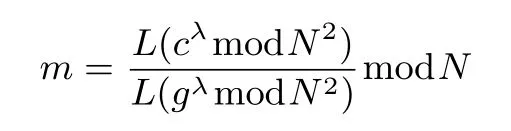
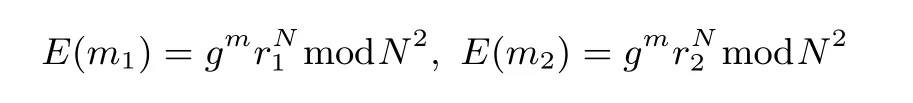
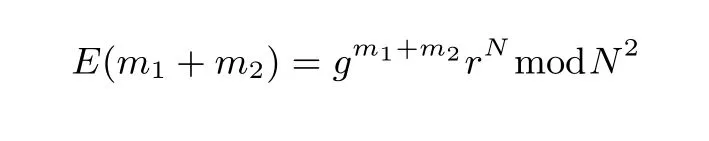
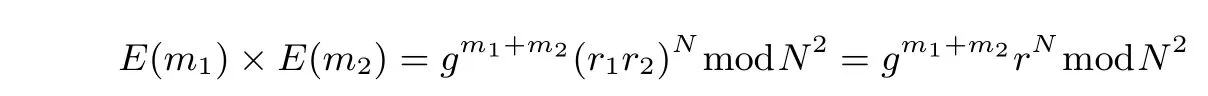

2.3 椭圆曲线同态加密算法

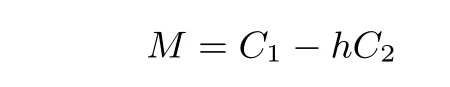
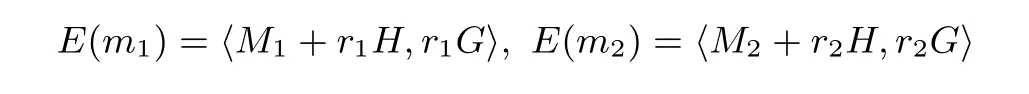

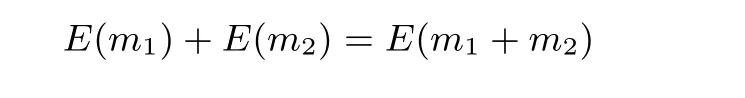
2.4 门限解密
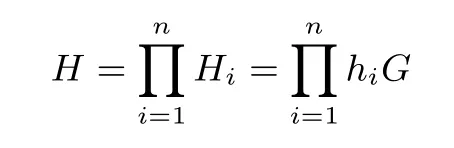
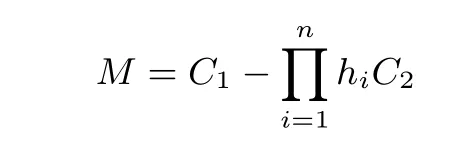
3 直方图保密生成协议
3.1 协议的基本原理






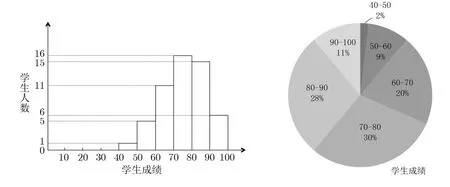
3.2 基本的直方图保密计算方案

3.3 方案分析
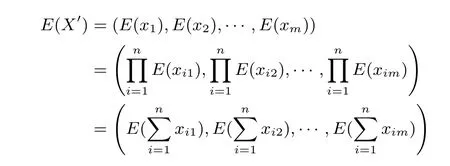

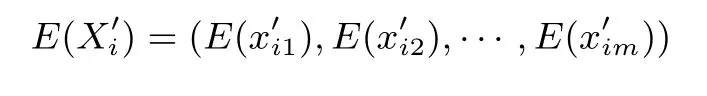
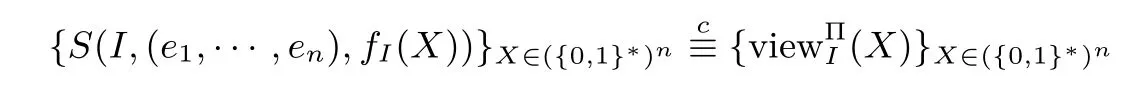
4 基于门限解密的直方图保密生成协议
4.1 基本原理与协议
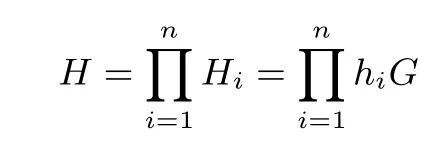
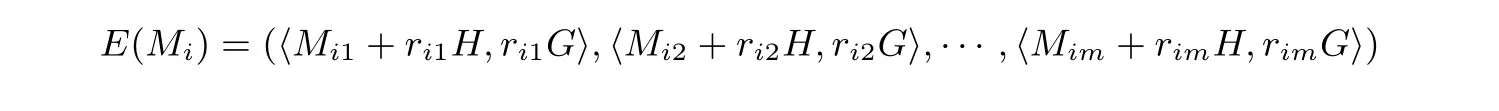
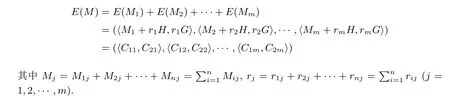
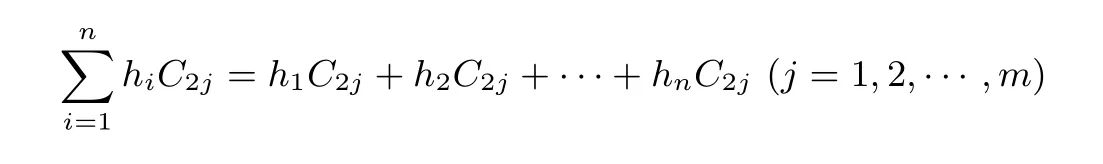
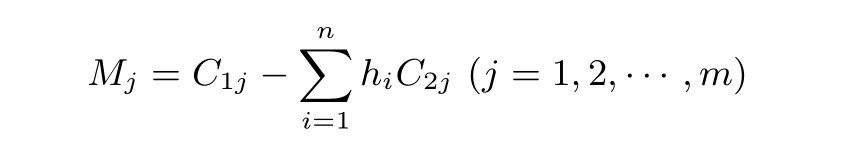
4.2 方案分析
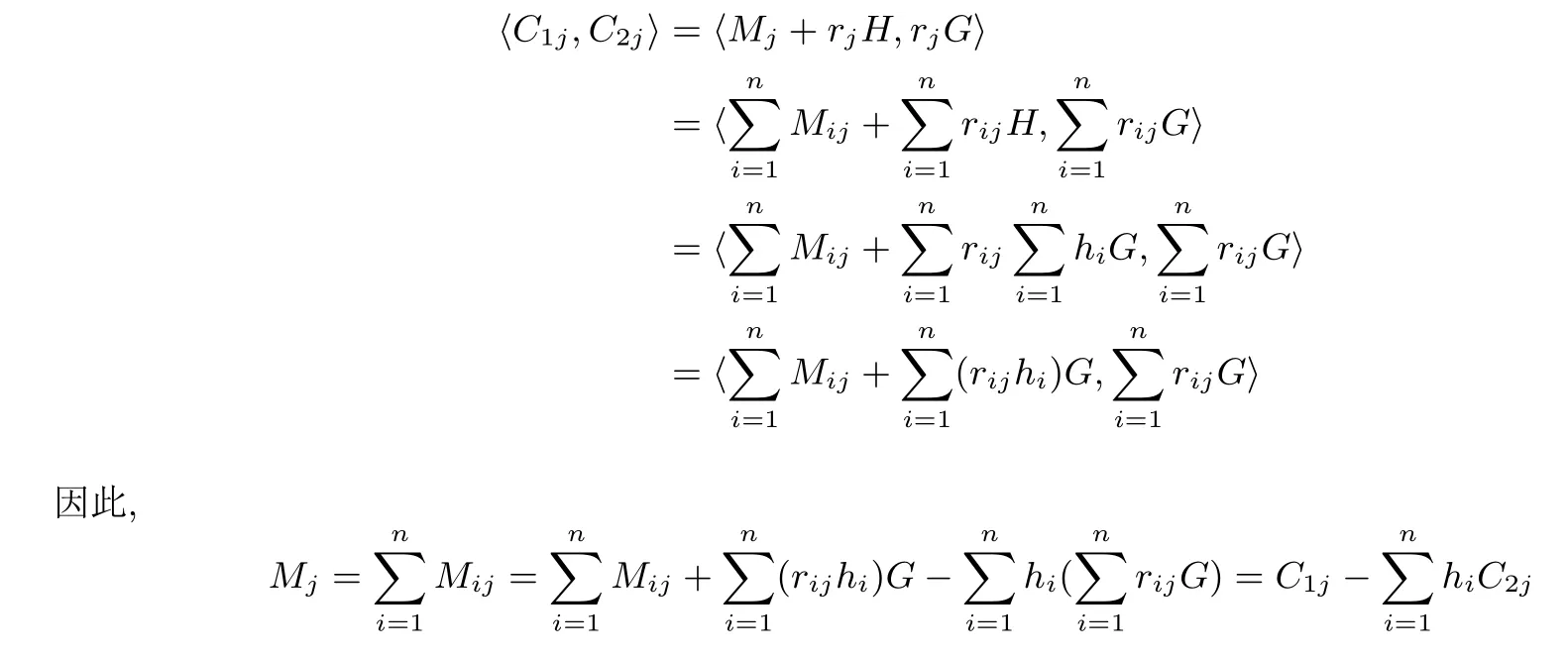
5 协议的效率分析
5.1 计算复杂性
5.2 通信复杂性

5.3 实验数据分析
6 结论
