导数在高中数学解题应用中的策略探究
2019-06-10柏雪
柏 雪
(重庆市为明学校,重庆 401122)
导数如此重要,是学习数学、研究数学的必不可少的一个工具,是初等数学和高等数学的一个连接纽带。学习导数知识可以在实际应用中快速准确求出函数的切线斜率,还可以准确又简便的求出曲线的切线方程,也可以求出函数的最大值、最小值、极大值以及极小值,即利用导数可以解决生产和生活中常见的能用数学知识解决的最优决策和最优设计问题。
一、定义法求导数
在高中数学的学习中,导数的定义是这样的:在函数f(x)中,在点x=x0处的导数就是f(x)在点x=x0处的瞬时变化率,记作当把上式式中的x0看作变量x时,即的导函数,简称导数,即
二、求解函数的切线斜率
函数的切线斜率的求解其实是利用了导数的几何意义,即:函数f(x)在点x0的导数是曲线y=f(x)在点(x0,y0)处的切线斜率。若θ表示这条切线与x轴正向的夹角,则,即这条切线的斜率是这个夹角的正切值。从而我们可以得出结论,当时,表明切线与x轴正向的夹角是一个锐角;当时,表明切线与x轴正向的夹角为一个钝角;当时表示切线与x轴平行,通过这个方法也同样可以求出曲线的切线方程,即首先要求利用导数的几何意义出函数的切线斜率,然后把已知的点坐标代入函数表达式中,即可求出函数的切线方程。具体有以下例子说明:
(1)求曲线在点P(2,4)处的切线方程;
(2)求曲线过点P(2,4)处的切线方程。
故所求切线方程为4x-y- 4 =0或x-y+2=0
三、判断函数单调性问题
我们都知道函数的单调性是指一个函数在某个区间内或者在其定义域内的单调性的变化规律,这是研究函数的图形时首先需要考虑的一个关键性问题。而且在中学的时候,我们已经学习并掌握了函数在某个区间内或定义域内的单调性的定义。现在,高中数学中导数的学习让我们更深入的了解其定义并且能更容易判断函数单调性及确定其单调区间。
我们现在可以深入挖掘一下函数导数在函数单调性中的应用涵义,假设函数y=f(x)在点区间[a,b]中可导,则会有以下三个结论:(1)若对区间(a,b)中所有的x而言f'(x)>0,则f(x)在(a,b)中递增;(2)若对区间(a,b)中所有的x而言f'(x)<0,则f(x)在(a,b)中递减;(3)若对区间(a,b)中所有的x而言f'(x)=0,则f(x)在(a,b)中不变。由此可见,只要能够求出函数的导数,即求出函数的切线的斜率,同时判断它大于0的还是小于0的,就能判断函数的单调性,这种方法不仅方便,而且更加直观。
例:已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.(1)若曲线y=f(x)与曲线y=g(x)在他们的交点(1,c)处具有公共切线,求a,b的值。(2)当a2=4b时,求函数f(x)+g(x)的单调区间.
解:(1)f′(x)=2ax,g′(x)=3x2+b,
由题知,f(1)=g(1),f ′(1)=g′(1),故a+1=1+b,2a=3+b
最后解得a=3,b=3,
(2)设,h(x)=f(x)+g(x),即h(x)=x3+ax2+bx+1,
a>0时,h(x),h′(x)的情况如下:
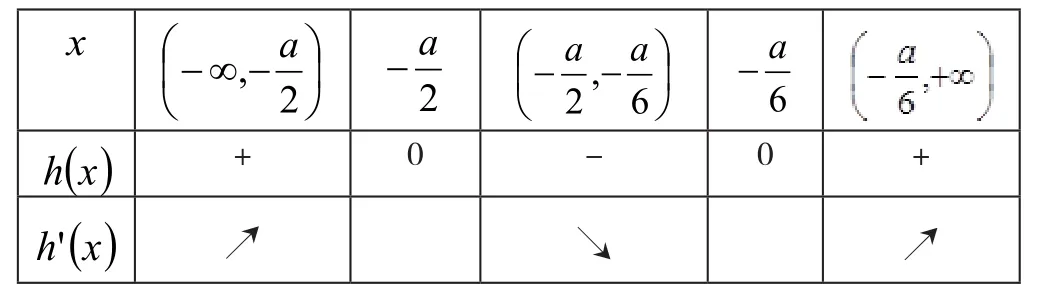
x ■■■■■-∞ -2,a■2 a-■■a■■■■- -6,2 a 6 a-()x h +0-0 +()x h'↗↘↗
所以函数h(x)的单调递增区间为单调递减区间为
四、求解函数的极值问题
函数值由增加到减少或者是由减少到增加,都经过一个转折点,即图中的“峰值”点和“谷值”点,这些点是在研究函数中是十分重要的。极值的求法是这样定义的:设函数f(x)在点x=x0及其区间左右两侧附近有定义,若对该区间内的任意点x(x≠x0)恒有f(x)<f(x0),则f(x0)为极大值;若f(x)>f(x0)成立,则f(x0)为极小值。由以下例子具体说明:

当0<x<1时,f'(x)<0,故f(x)在(0,1)上为减函数;
当x>1时,f'(x)>0,故f(x)在上为增函数;
从而f(x)在x=1处取得极小值f(1)=3,无极大值。
五、求函数的最值问题
在经济活动和日常生活中,我们常常遇到这些问题,例如:如何合理的使用原料才能达到最省,而且成本最低,效率最高或者是效益效率最好的目的的问题,这些问题在数学学习中,称为函数的最大值或最小值问题,即最值问题。假定函数f(x)在闭区间[a,b]上连续,则必存在最大、最小值,其判定的一般步骤和方法是:①求导数f'(x);②求方程f'(x)=0的根;③检验f'(x)在方程f'(x)=0的根的左右符号。若在根左侧附近大于0,右侧附近的值小于0,那么,函数y=f(x)在这个根处能够取得极大值;若在根左侧附近的值小于0,右侧附近大于0,那么函数y=f(x)在这个根处能够取得极小值。对于在闭区间[a,b]连续,在开区间(a,b)内可导的函数对f(x)的最大值和最小值,可以首先求出函数在开区间(a,b)上的极大(小)值,并与函数定义域端点值f(a),f(b)比较,即可得出最大(小)值.由以下例子具体说明:
解:f(′x)=ex+xex=(x+1)ex,令
当-2≤x<-1时,f′(x)<0,f(x)在[-2,-1]上是单调递减函数;
当-1<x≤2时,f′(x)>0,f(x)在(-1,2]上是单调递增函数;
所以,x=-1为f(x)的极小 值点,即
所以,函数f(x)在[-2,2]的最小值
最大值f(x)max=f(2)=2e2
结语:总之,高中数学中导数的学习,不仅拓展了学生学习数学和解决数学问题的思路,而且还扩展了学生的数学知识,让学生体味到数学学习的乐趣,进一步了解数学极限思想和方法,对学生是十分有帮助的。
