基于功率控制的认知无线网络能效研究

韩宾　邓冬梅　江虹

摘   要：针对Underlay频谱共享模式下的认知无线网络的能量效率问题，提出了一种双重改进的粒子群功率控制优化算法（Dual Improved Particle Swarm Optimization， DIPSO），通过最小化约束条件下认知用户的发射功率以实现网络能量效率优化.在仿真过程中，以保证认知用户基本通信的同时不对主用户正常通信构成影响为基本前提，对信道衰落及噪声干扰进行了综合考虑，搭建出多约束条件下的网络能量效率函数，实现认知无线网络中认知用户发射功率的最小化.仿真结果表明：该算法可有效提升无线网络的能量效率.

关键词：认知无线电;DIPSO;功率控制;能效优化

中图分类号：TN915.5                          文献标志码：A

Study on Energy-efficient of Cognitive Wireless

Networks Based on Power Control

HAN Bin1，2， DENG Dongmei2， JIANG Hong2

（1. State Key Laboratory of Environment-friendly Energy Materials，Southwest University of Science

and Technology，Mianyang 621010，China;

2. School of Information Engineering，Southwest University of Science and Technology，Mianyang 621010，China）

Abstract：Aiming at the problem of cognitive wireless network energy efficiency under underlay spectrum sharing mode，a double improved particle swarm optimization algorithm（DIPSO） for power control was proposed.  The optimization of network energy efficiency was realized by recognizing the transmitted power of users under the condition of minimizing constraints. In the simulation process，under the circumstance of considering channel fading and noise interference，the fuction of network energy efficiency and relevant constraints were constructed on the premise where the normal communication of main users was not affected，the basic communication of users was guaranteed， and the transmission power of cognitive users in the cognitive wireless network was minimized. The simulation shows that the proposed algorithm can effectively improve the energy efficiency of wireless network.

Key words：cognitive wireless radio;dual improved particle swarm optimization（DIPSO）;power control;energy-efficient optimization

隨着无线网络应用和需求的不断发展，无线网络对提升通信速率、提高频谱利用率的要求也日益增强.同时，通信网络的能耗也已成为必须考虑的问题，网络能量效率更是成为衡量通信网络能耗的一项重要指标[1].认知无线电技术的发展，将传统无线网络中的用户按用频优先权的不同分为：1）对频谱具有绝对优先使用权限的主用户（Primary User，PU）;2）利用频谱感知与判决结果伺机而动共享主用户频谱的认知用户（Second User，SU）[2].认知用户利用动态频谱接入技术，实现与主用户共享频谱，以提高频谱资源紧缺背景下频谱资源的利用率.频谱共享方式目前主要分为Overlay（覆盖式）及Underlay（共存式）两种.Overlay中主用户和认知用户在同一时隙中不共存，认知用户只能在主用户不占用信道时才能伺机接入并使用其信道进行传输.Underlay模式则允许认知用户在不影响主用户通信的前提下与主用户共享同一频谱[3].在Underlay频谱共享方式中，认知用户发射功率的大小将直接影响到主用户及认知用户的通信情况.发射功率过低可能无法保证认知用户的通信质量，发射功率过高又将对主用户的正常通信造成同频干扰.认知用户必须保证对主用户造成的累计干扰功率之和能在主用户允许的门限范围内，还要尽可能地满足自身的通信要求[4]，更何况还需考虑认知用户间的干扰抑制和可用频谱间的差异.因此认知无线网络中的认知用户的发射功率必须受到严格约束，功率控制问题成为了一个复杂的多维多目标的优化问题.而网络能量效率的高低与发射功率的大小密不可分，因此，Underlay频谱共享模式中，在有效保护主用户通信质量的前提下，如何实现对认知用户的发射功率进行合理有效控制，成为了认知无线网络中必须要考虑的重要问题.

近几年，针对CRN（Cognitive Radio network）功率控制策略方面的研究已取得一定的成果，这些研究可以从合作方式和算法类型上进行分类.从合作方式上分为合作式功率控制及非合作式功率控制，从功率控制算法上又分博弈论、群智能、凸优化等等. LUO等人[5]以用户信干噪比（Signal to Interference plus Noise Ratio，SINR）为目标，利用博弈论提出了两种线性成本函数功率控制算法，达到最小化发射功率的目的.诸一琦[6]通过对SU的服务质量需求（Quality of Service，QOS）和通信系统的总吞吐量进行综合考虑，提出一种非合作功率控制博弈的CRN功率控制算法来对各SU的发射功率进行控制.文献[7]在用户可接受的QOS体验约束条件下，最大限度减少传输的能量消耗，提出一种在线策略迭代算法，直接優化服务质量约束下的能量消耗.文献[8]联合遍历容量和最大限度地减少次用户网络的平均传输功率的同时提高网络能源效率，将多目标优化转化为单目标优化问题.

现有文献中，将能量效率作为效益目标而进行多约束条件下的功率控制的研究还相对较少，因此本文在考虑了无线电信号传播过程中的自由衰落的前提下，针对Underlay频谱共享模式下的认知无线网络，基于干扰温度模型提出了一种双重改进的粒子群功率控制优化算法（DIPSO），实现网络能量效率优化.

1   系统建模与分析

1.1   网络模型

图1所示为Underlay频谱共享模式下CRN传输模型，多个SU与PU共存并共用同一信道.SU1、SU2为认知用户，PU为主用户，实线箭头代表用户之间正在使用信道进行通信，虚线箭头代表正在通信的用户对使用了同一频谱的其他用户造成的通信干扰.SU用户感知外界通信环境的变化，如主用户出现与否，根据感知情况进行自身决策，当主用户未占用频谱资源下，对主用户的干扰就不必考虑，此种情况下，SU用户的功率约束就相对简单很多.当主用户出现时，SU用户则必须考虑对主用户的干扰，在综合衡量下，利用寻优决策出最优的发送功率，以达到既保证通信质量又减少不必要的能量消耗的目的.因此SU的寻优决策结果，关系着SU对外界通信环境变化自身发射功率的调整，对网络能量效率尤为关键.

假设信号传输满足自由空间衰落模型，则信号发射端发射功率与接收端接收功率之间满足

式中：pr 表示接收端接收功率;pt表示发射端发送功率;d表示接收端与发射端之间的距离，c为光速;f为电磁波发射频率;Gr、Gt分别表示接收端天线增益、发射端天线增益.

1.2   数学模型

由M个主用户PU和N个认知用户SU构成的认知无线网络中，PU和SU采用Underlay频谱共享模式.该模型中认知用户SU必须满足不能对主用户PU的正常通信产生影响，因此，PU接收机端接收到的来自SU发射机端的总干扰有以下的约束条件，即

式中：pi表示第i个认知用户发射机的发送功率，i∈[1，N];Gik代表第i个认知用户发射机和第k个主用户接收机之间的信道增益;P kth代表第k个主用户发射机的干扰功率允许的最大阈值.由于认知用户必须满足自身的通信质量要求，因此每个认知用户接收机的信干噪比值（SINR）需满足以下约束条件：

γ i   th≤ γiγ i   th > 0               （3）

式中：γ i   th表示在链路i上认知用户接收机最小的信干噪比阈值;γi表示在链路i上认知用户的实际信干噪比值.γi的计算方式如下：

式中：pi表示认知链路i上发射机的发射功率;Gi代表认知链路i上SU发射机与接收机之间的信道增益;δ2代表认知链路i上的加性高斯白噪声;pjGji表示认知链路i上接收机接收到来自认知链路j的干扰;pj代表认知链路j上发射机发送功率;Gji表示从认知链路j上发射机到认知链路i上接收机之间的干扰增益;pkGki表示认知链路i上接收机接收到来自主链路k的干扰;pk表示主链路k上发射机的发射功率;Gki表示从主链路k上发射机到认知链路 上接收机之间的干扰增益.

根据香农公式，认知链路i上的最大传输速率 si必须满足：

si = Wi log2（1 + γi）         （5）

式中：Wi表示每个子信道的带宽，根据公式（5）可以得出功率与传输速率之间的关系.

每个认知用户发射机传输功率不能够超过其发射机所允许的最大功率阈值，设pmaxi      为每个认知用户发射机的最大传输功率，因此有

0 ≤ pi ≤ pmaxi                  （7）

利用网络吞吐量与能量消耗的关系，以单位功耗内的吞吐量构造网络能量效率

为提升网络的能量效率，本文拟在满足上述约束条件下，最小化链路的平均传输功率.最后，优化问题可以归纳为下面约束条件下的联合优化.

2   改进的粒子群功率控制优化算法

生物启发式算法中的粒子群优化算法（PSO，Particle Swarm Optimization）由于搜索速度快、寻优效率高而被广泛用于解决优化问题.通过种群中不同个体间的相互协作实现最优解的搜索.算法初始时在可行空间解中随机初始化m个粒子组成的种群 Z = {Z1，Z2，…，Zm}，其中每个粒子的位置代表待优化问题的一个解.然后每个粒子根据目标函数计算自身的适应度值，根据所得出的适应度值，粒子在空间中不断调整自身位置以搜索新解.每一次迭代中，粒子将跟踪粒子本身经过搜索得到的最优解 pid（局部极值）和整个种群目前搜索到的最优解pgd（全局极值）这两个“极值”来更新自己[9].此外，每个粒子都有一个速度Vi = {Vi1，Vi2，…，Vim}，当两个最优解都找到后，每个粒子根据公式（10）更新自身的速度，根据公式（11）更新自身位置.

vid（t + 1） = ωvid（t） + η1rand（）[pid - zid（t）]

+ η2rand（）[pgd - zid（t）] （10）

zid（t + 1） = zid（t） + vid                   （11）

式中：vid（t + 1）表示第i个粒子在t + 1次迭代中第d维上的飞行速度;ω为飞行速度的惯性权重;η1、η2 为加速常数;rand（）为0～1之间的随机数;zid（t + 1）表示第i个粒子在t + 1次迭代中第d维上的位置.此外，为使粒子速度不至于过大，对飞行速度设置上限阈值vmax，即当v id（t + 1） > vmax時，根据式（12）进行粒子速度限制.

vid（t + 1） = vmaxvid（t + 1） = -vmax             （12）

从式（10）（11）粒子的飞行速度和位置更新公式可以看出，粒子的移动主要受自身当前飞行速度 vid、自身当前位置与局部遍历过的最优位置的距离 pid - zid（t）和自身当前位置与群体最优位置的距离pgd - zid（t） 三部分影响.分别由权重系数ω和η1、η2决定其相对重要性.当达到了最大迭代次数或找到足够好的最优解时算法结束.

PSO算法在优化早期能够迅速向最优值靠近，但是由于缺少种群的多样性，在最优值附近收敛较慢，容易出现所谓的早熟现象的缺点.为了有效平衡PSO算法的全局搜索能力和局部搜索能力，权重线性递减粒子群算法和自适应惯性权重粒子群算法[10]分别被提出，它们均采用式（10）更新粒子速度.

针对PSO算法收敛速度慢和容易陷入局部最优的缺点，本文从改进惯性权重ω及增加种群多样性两个方向对算法进行改进.将改进后的算法称为双重改进粒子群算法（DIPSO）.

1）惯性权重参数修改.由于权重线性递减粒子群算法中，惯性权重参数 关系到算法在全局搜索能力和局部搜索能力上的平衡.考虑到指数函数的函数单调性，将指数函数y = ex引入权重线性递减粒子群算法的惯性权重表达式中，令自变量x=.由于迭代次数t满足0≤t≤tmax，因此自变量x的变化范围为x∈（-∞，0]，函数y则在区间（0，1）上呈指数函数性质的单调递增函数，因此改变了原来ω的线性变化规律，将其引入权重线性递减粒子群算法的惯性权重表达式，得到：

ω = ωmax - （ωmax - ωmin）×exp（（t - tmax）/t） （13）

式中：ωmax、ωmin分别表示惯性权重ω的最大值和最小值;tmax代表最大迭代次数;t为当前迭代次数.

2）增加种群多样性.本文引入种群初始化的混沌优化算法，它比随机搜索更有利，能够提高粒子群算法的局部寻优能力.其基本思想是采用Logistic映射生成混沌变量，如式（14）所示：

cxt+1id    = μ × cxtid  × （1 - cxtid ）            （14）

式中：μ代表控制参数;cxtid 代表整个混沌序列中的第i个混沌变量在第t次混沌搜索中的第d维中的分量.然后通过线性变换将混沌变量映射为粒子的位置变量，如式（15）所示：

xt+1id    = xminid    + cxt+1id   × （xmaxid    - xminid   ）       （15）

式中：xminid   和xmaxid   分别表示搜索空间中每一维度的最大值和最小值;cxt+1id   是整个混沌序列中的第i个混沌变量在第t+1次混沌搜索中第d维中的分量.

DIPSO算法流程图如图2所示.

3   仿真结果与分析

假设在Underlay频谱共享模型的CRN中存在1个PU链路和3个SU链路，即M=1，N=3.仿真过程中节点采用随机分布，采用仿真中模拟的节点间的测量距离.参数值部分依据文献[11-12]进行类似设置，仿真参数设置如表1所示.

表中：pi     max代表每个SU发射机的最大发射功率;pk   th代表每个PU接收机能允许的最大干扰功率;γi   th表示每个SU接收机的最小信干噪比;加性高斯白噪声为δ2;子信道带宽为Wi;认知链路i的发射极到主链路k的接收机之间的干扰增益为Gik;认知链路j的发射机到认知链路i的接收机之间的干扰增益为Gji;所有PU发射机对活跃SU接收机的干扰功率为Q.

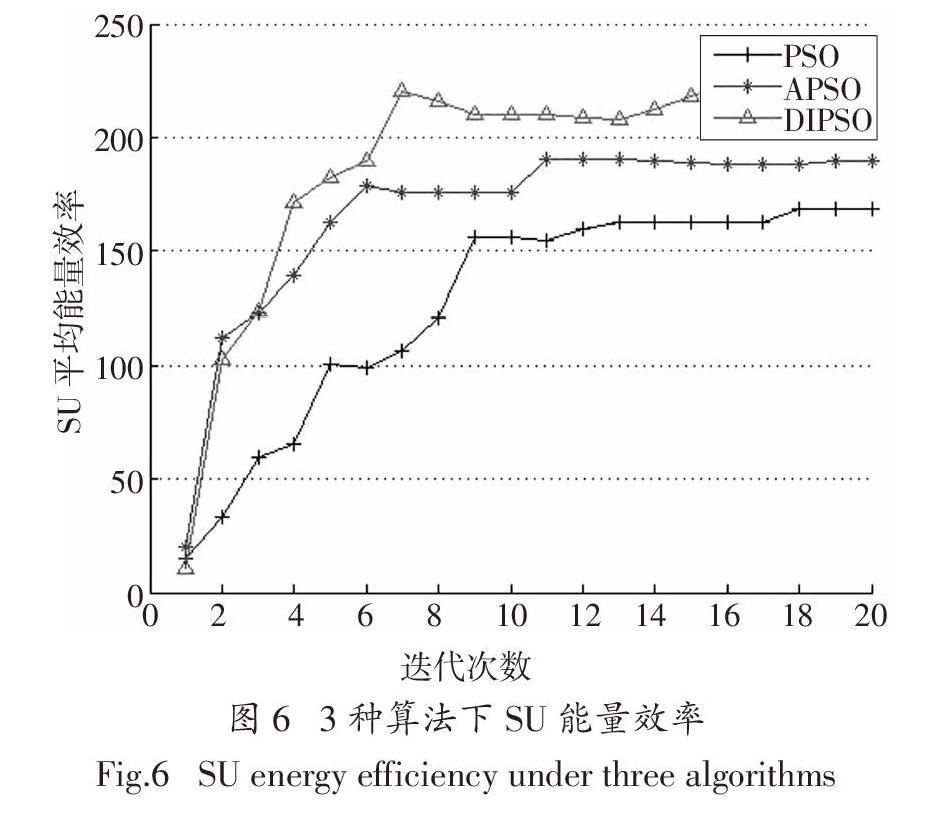
本文提出的DIPSO算法中，粒子个数是20个，迭代次数是20次，加速常数为η1、η2.在APSO算法中最小惯性权重ωmin，最大惯性权重ωmax.在PSO算法中，惯性权重ω = 0.9，设粒子速度上下限为[Vmin，ωmin]=[1，-1].仿真结果如图3～图6所示.

由图3可知，无论是采用DIPSO、APSO还是采用PSO算法，认知无线网络中SU的信干噪比（SINR）均大于门限阈值，足以说明SU可以获得良好的通信.

图4表明认知无线网络中的认知用户在每一次迭代过程中的总发射功率.能量消耗等于发射功率与单位时间的乘积，因此功率最小化是本文优化的主要目标.从图中可以看出DIPSO算法的SU总发射功率小于APSO算法和PSO算法，因此相比之下DIPSO算法耗能更低而且DIPSO相较于另外两种算法能更快地趋于稳定且稳定性能相对略高.