基于响应面模型的滑移门动力学特性多目标优化

陈梓铭　郭鹏程　熊勇　李会玉　李落星

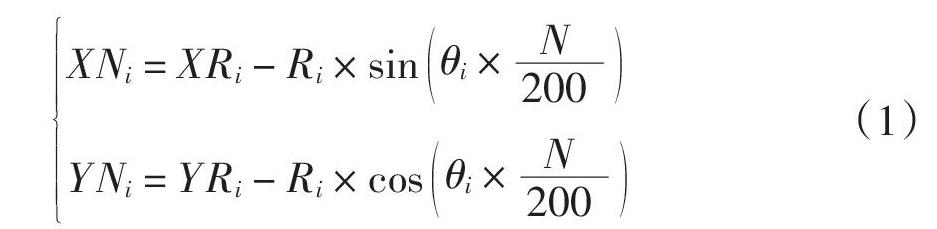
摘   要：为了在满足开启轻便性的条件下提升滑移门的运动平顺性，提出了基于响应面模型的滑移门动力学特性多目标优化方法.基于刚柔耦合多体动力学方法建立某MPV车型的滑移门模型，对其运动平顺性及开启轻便性的评价指标进行分析，并通过滑移门台架试验验证了该仿真方法的可靠性.对滑移门运动机构进行参数化设计，结合拉丁超立方采样法进行试验设计，通过对滑移门动力学特性指标进行灵敏度分析，得到了结构参数对性能的影响规律.建立精度可靠的滑移门动力学特性二阶响应面模型，各项指标的复相关指数R2 均高于0.9.采用NSGA-Ⅱ遗传算法对滑移门运动机构进行多目标优化，滑移门中导向轮载荷峰值与质心加速度峰值分别降低39%和24.4%，全开所需时间低于1.8 s，在满足开启轻便性要求的同时，显著提升了滑移门的运动平顺性.

关键字：滑移门;动力学分析;结构参数;响应面方法;多目标优化

中图分类号：TB21                            文献标志码：A

Multi-object Optimization on Dynamic Characteristics

of Sliding Door Based on Response Surface Model

CHEN Ziming1， 2，GUO Pengcheng1， 2，XIONG Yong3，LI Huiyu1，2，LI Luoxing1，2

（1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University，Changsha 410082，China;

2. College of Mechanical and Vehicle Engineering，Hunan University，Changsha 410082，China;

3. Changan Oushang Automobile Institute，Chongqing 400023，China）

Abstract： In order to optimize the ride comfort of the sliding door under the condition of meeting the handiness requirement，a respond surface method-based multi-object optimization method of the sliding door′s dynamic characteristics was proposed. The rigid-flexible coupled multi-body dynamic model of a MPV′s sliding door was established to investigate its ride comfort and handiness，and the results were verified by experiment based on a test rig. The motion mechanisms of the sliding door system were parametrically modeled and combined with the Latin hypercube sampling method. The sensitivity analysis was performed to study the effects of structural parameters on the sliding door's dynamics characteristics. Second-order response surface models of the dynamic indexes were established，in which correlation coefficients R2 are above 0.9. Finally，a multi-objective dynamic optimization on the sliding door was conducted by using NSGA-II algorithm. After optimization，the peak values of the middle guide roller load and acceleration of the door center mass were reduced by 39% and 24.4% respectively，and the time required for full opening was below 1.8 second. The ride comfort of the sliding door was improved significantly，while the requirement of handiness was met.

Key words： sliding door;dynamic analysis;structural parameter;response surface method;multi-object optimization

運动平顺性和开启轻便性是汽车滑移门重要的动力学特性，对客户在使用滑移门时的主观感受及产品的使用寿命有重要影响.在传统的滑移门运动机构的设计过程中，由于缺乏对滑移门动力学特性的管控，往往是在实车下线后才暴露出其运动平顺性差和开启困难的问题.因此，在前期设计阶段对滑移门系统的动力学特性进行分析和优化，有利于降低问题整改成本，缩短开发周期，提升车型的产品竞争力.

随着配置有滑移门的MPV车型在市场上的占有率逐步提升，国内外学者对汽车滑移门系统开展了研究.Muneer等[1]基于试验方法对滑移门最小关闭速度的影响因素进行了探究，研究表明气压阻力是其中最主要的因素. Suzuki等[2]提出了一种应用位置传感器和开度控制系统的推拉绳索式电动滑移门系统，显著减小了驱动装置的尺寸和重量.近年来，一些学者对滑移门的动力学特性开展了研究.刘鹏飞等[3]建立了滑移门的运动学数学模型和多刚体动力学模型，通过仿真分析揭示了滑移门在过弯时平顺性降低的机理.蒋东升等[4]基于滑移门动力学模型，研究了各滚轮在运动过程中的受力情况，发现中铰链的前导向轮载荷远大于后导向轮.为优化滑移门性能，廖鸿胡等[5]运用正交试验设计方法，研究中导轨和中铰链销的布置对滑移门平顺性的影响规律，实现了针对滑移门运动轨迹曲率的优化.高云凯等[6]采用刚柔耦合动力学方法对滑移门系统进行建模，考虑滑移门在运动过程中的弹性变形，提升了动力学特性的仿真分析精度.文献[7]对滑移门平顺性的多目标优化方法开展研究，提出了基于正交试验设计和分级解密方法的铰链销位置优化方法，以及基于评价函数方法的导轨结构优化方法.在这些优化工作中，由于滑移门动力学特性的非线性程度极高，以及正交试验设计的样本数量较少，所以无法构建精确的代理模型，导致难以运用常规多目标优化算法找到兼顾运动平顺性与开启轻便性的滑移门运动机构方案.

本文针对滑移门动力学特性优化困难的问题，提出基于响应面的多目标优化方法.建立滑移门导轨的参数化建模方法，显著提升滑移门动力学仿真试验设计的效率，为构建可靠的滑移门动力学特性拟合模型提供充足的样本数据.随后基于高精度拟合模型，实现了滑移门动力学特性的多目标优化，在满足开启轻便性要求的同时，显著提升了运动平顺性，对滑移门运动机构的结构设计和布置有重要指导意义.

1   滑移门动力学特性分析及试验验证

1.1   滑移门系统刚柔耦合多体动力学建模

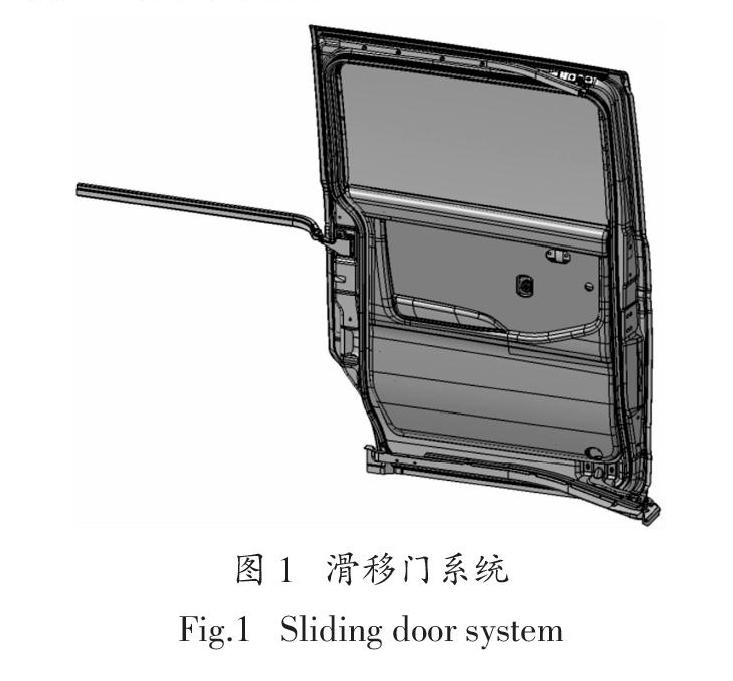
滑移门系统一般由滑移门、铰链和导轨组成.滑移门主体包括门体焊接总成、门锁机构、内外饰及玻璃升降器等部件，通过上、中、下支撑臂与3条导轨进行配合，以实现其运动导向和支撑自重.对于一般的MPV车型，滑移门上支撑臂为钣金冲压件，臂上安装有1个导向轮;滑移门的中、下支撑臂则为铰链结构，在阳铰链上安装有2个导向轮与1个承重轮.图1所示为一款紧凑型MPV车型的滑移门系統，该滑移门的质量为31.3 kg.为研究该滑移门系统的动力学特性，需基于Adams/View软件平台对其进行刚柔耦合动力学建模.

为了提升动力学仿真的精度，需对滑移门和铰链进行柔性化处理，因此在有限元前处理软件Hypermesh中对滑移门主体结构和铰链进行建模，再提交给有限元分析软件Nastran求解，生成它们的MNF（模态中性文件）[8].MNF可由Adams/View在动力学仿真时调用，以实现滑移门和铰链在运动过程中的弹性变形行为.为了减少计算成本，在有限元建模时将滑移门的锁体、内外饰和电器简化为质量点，并根据实际连接情况，通过RBE2或RBE3与门体进行连接，装配完成的滑移门有限元模型如图2所示.

滑移门系统的导向轮、承重轮及导轨均采用刚性建模，以降低计算资源消耗，以及避免仿真中出现由于网格粗糙而导致的异常接触力.

如图3所示，在Adams/View中通过旋转副对门体、铰链和各个滚轮进行装配，以实现铰链和滚轮的旋转运动.需要注意的是，直接将CAD（计算机辅助设计）数据导入Adams/View生成的导轨，由于其几何特征粗糙，会导致仿真中的滚轮接触力出现较多的毛刺.采用Adams/View中的Extrusion挤出功

能进行建模，可以获得几何平滑的导轨刚体模型，如图4所示.最后建立了各滚轮与导轨之间的接触关系，形成完整的滑移门系统刚柔耦合多体动力学模型，如图5所示.

1.2   滑移门系统动力学特性分析

以滑移门在关闭过程中的中导向轮载荷峰值和质心合加速度峰值作为其运动平顺性的评价指标.其中，中导向轮是指滑移门中铰链的前导向轮，其载荷远大于后导向轮[4]，对滑移门运动过程中的抖动、异响和导向轮的磨损有极大影响.滑移门的质心合加速度变化情况则反映其在运动过程中抖动的强弱程度，直接影响使用者的操作手感和观感.另外选择滑移门全开所需时间作为开启轻便性的评价指标，滑移门在特定加载方式下由关闭状态运动至全开状态所需的时间，可以反映其开启的难易程度.

基于已建立的滑移门系统动力学模型进行关闭过程仿真，在门把手处施加沿车长方向朝车头，初值为40 N的拉力.通过函数step（time，1，40， 1.1，0）对该拉力进行控制，以模拟使用者在滑门关闭前松开把手的过程.经过仿真分析，该滑移门系统的中导向轮载荷和门体质心合加速度分别如图6和图7所示，它们在运动过程中存在极大的突变，该突变出现在中导向轮进入过弯处时，峰值分别为552.6 N和1.63g.研究表明，过高的峰值会对滑移门的运动平顺性和使用寿命有不良影响[9].另对该滑移门的开启过程进行仿真分析，加载工况为在门把手处施加沿车长方向朝车尾，大小50 N的恒定拉力，该滑移门从关闭位置运动至全开状态所需时间为1.95 s.

1.3   滑移门系统动力学特性试验验证

为验证滑移门系统动力学仿真分析结果的准确性，需对其进行试验对标.为了规避车身装配误差对滑移门运动性能的影响，将滑移门安装在试验台架上进行测试.由于直接测量中导向轮载荷较困难，且定制力传感器的成本较高[10]，本试验选择的测量项为滑移门外板上的测点在关闭过程中的加速度，以及滑移门的全开所需时间.滑移门测试台架如图8所示，滑移门外板上共有5个测点，其中，B测点与滑移门的几何中心和质心都非常接近，其加速度变化情况可以反映滑移门整体的抖动情况.在各测点处安装加速度传感器，传感器局部坐标系中的Xs、Ys和Zs轴的正方向分别为竖直向上、沿车长方指向车头和沿车宽指向外侧，该局部坐标系会跟随滑移门的运动而移动.

基于台架进行多次滑移门开启和关闭试验，全开所需时间的平均值为2.1 s，仿真试验误差为7.1%.在试验中，滑移门在过弯时有明显的抖动和异响现象，与仿真分析结果中的中导向轮和加速度出现突变的现象一致.由于采集加速度信号时伴隨有噪声及干扰，需要对加速度信号进行低通滤波和去趋势化处理.图9所示为B测点在关闭过程中的加速度变化情况，由于中导向轮进入中导轨圆弧段时，滑移门的运动轨迹发生了突变，导致测点处各方向的加速度都发生剧烈变化.其中Zs方向加速度的突变情况最严重，峰值达到-1.722g.

图10所示为B测点加速度的仿真试验对标情况，仿真分析得到该测点Xs、Ys与Zs 3个方向加速度曲线与试验测量结果趋势一致.在加速度突变最剧烈的Zs方向，仿真分析的加速度峰值为-2g，与实测结果的误差约为16.1%.其它测点的加速度对标情况与B测点类似，各方向的加速度曲线仿真结果与实测曲线趋势一致，且Zs方向加速度峰值的误差低于18%.根据滑移门全开所需时间和外板测点加速度的对标情况，该滑移门刚柔耦合动力学模型能反映滑移门在运动过程中的动态特性，可用于指导滑移门系统的性能优化工作.

2   滑移门系统动力学特性灵敏度分析

滑移门运动机构的结构参数较多，如果对这些参数与其动力学特性之间的关系缺乏认识，就无法在前期设计阶段对滑移门运动机构进行合理设计，导致后期优化困难.因此，需要对滑移门动力学特性的影响因素进行灵敏度分析.

2.1   滑移门运动机构参数化设计

滑移门系统的动力学特性非线性程度高，因此对其运动机构的结构进行参数化设计，有利于增加试验设计的样本量，以提升灵敏度分析结果的可靠性.滑移门系统的导轨一般由两条直线段与它们之间的圆弧段组成，其中圆弧段的半径和两直线段的夹角为导轨的主要结构参数.该仿真模型中的导轨是由Extrusion功能创建，因此通过对执行该功能时所需的导轨轨迹线进行参数化设计，就能实现对导轨结构的控制.在Adams/View中，通过Polyline样条线功能建立导轨轨迹线，并对样条线上各点的坐标进行参数化设计.其中，导轨圆弧段的轨迹线由200个等分点和相邻点之间的连线组成，其中任意第N个点PN的坐标如式（1）所示：

式中：XRi、YRi、Ri和θi分别为第i条导轨轨迹线的圆弧段圆心Oi的X坐标、圆心Y坐标、圆弧半径和直线段夹角（如图11所示），i的取值为1、2、3，分别表示滑移门系统的上、中、下导轨;设计变量di，表示滑移门关闭状态下，铰链前导向轮与导轨前端的距离，通过改变该参数可以调整导向轮和铰链的初始位置.

如图12所示，对中、下臂的阳铰链结构进行参数化设计，drj为导向轮的间距;wlj为铰链销距导向轮中垂线的距离;wkj表示铰链销与导向轮中心连线的距离.下标j的取值为2、3，分别表示滑移门系统的中、下铰链.值得注意的是，由于下臂铰链销一般位于导向轮中垂线上，因此wl3的值为0，不需要进行参数化设计.

通过对滑移门系统的导轨和铰链进行参数化设计，共得到滑移门运动机构的14个结构参数.

2.2   灵敏度分析

采用多目标优化软件Isight与Adams/View进行集成进行试验设计（DOE），选择合适的试验设计方法有利于提升灵敏度分析的效率和准确性.常用的试验设计方法包括全因子设计、部分因子设计、正交数组设计和拉丁超立方设计.其中，拉丁超立方设计是一种多维分层抽样方法，能够使各个因素相对均匀地填满整个试验区间，而每个试验变量的水平只出现一次（如图13所示）.

采用拉丁超立方设计方法对滑移门运动机构的14个结构参数构造样本点矩阵，并进行多体动力学仿真分析，样本数量为600个.如图14所示，分别为该14个结构参数对滑移门中导向轮载荷峰值F、质心加速度峰值A及全开所需时间T的Pareto图，图中只展示影响最大的前10个一阶因素.根据各指标的结构参数影响排序可知，对中导向轮载荷峰值影响最大的结构参数是中铰链销至中导向轮中垂线的距离wl2和中导向轮间距dr2;对滑移门质心加速度影响最大的结构参数是上、下导轨的直线段夹角θ1和θ3;对滑移门开启所需时间影响最大的是结构参数是中铰链销至中导向轮中垂线的距离wl2和中导轨倾斜角θ2.而下导轨的半径R3及导向轮轮距dr3对滑移门系统的各项动力学特性指标的影响均极小.

3   滑移门动力学特性多目标优化

3.1   响应面拟合模型

根据所得的样本点数据，采用式（2）对滑移门的3个动力学特性指标进行二阶响应面拟合：

式中：y为响应输出;xi和xj为不同设计变量;c0、ci 和cj为常系数.另随机选取100个新样本点，运用R2误差分析方法对拟合模型的精度进行分析.分析结果如图15所示，中导向轮载荷峰值F、滑移门质心加速度峰值A和全开所需时间T的决定系数R2分别为0.98、0.916和0.966，说明该二阶响应面拟合模型的可信程度较高，可以取代滑移门系统的刚柔耦合动力学模型进行优化工作.

3.2   基于遗传算法的滑移门系统多目标优化

为了改善滑移门的运动平顺性和导向轮磨损情况，以中导向轮载荷峰值F最小，以及滑移门质心加速度峰值A最小作为优化目标;同时要满足滑移门的开启轻便性要求，以全开所需时间T低于

1.8 s作为约束条件.将滑移门运动机构的14个结构参数作为设计变量，建立的多目标优化数学模型

如下：

Variable： Ri，θi，di，drj，wlj，wkj

Objective： min F，A

s.t： T ≤1.8 s

i = 1，2，3; j = 2，3

采用NSGA-II（第二代非支配遗传算法）优化方法对该数学模型进行迭代寻优求解[11]，群体规模为16，最大遗传代数为30，而交叉率设置为0.9.对基于响应面模型进行优化所得到的滑移門系统结构参数进行规整化处理，并代入滑移门系统动力学分析模型中进行计算，优化效果如表1所示.

滑移门的中导向轮载荷峰值和滑移门质心加速度峰值分别由552.6 N和1.63g降低至337.1 N和1.23g，降幅分别为39%和24.4%;滑移门全开所需时间由1.95 s降低至1.78 s，满足了开启轻便性的要求.对该优化方案进行运动干涉分析，滑移门在过弯阶段与侧围的距离大于1 cm，无干涉风险.但是由于滑移门运动机构优化方案与原方案差异较大，导致试验样件制造成本过高，因此暂未对优化方案进行试验验证.

4   结   论

1）在Adams/View软件中建立某MPV车型滑移门系统的刚柔耦合仿真模型，并对其运动平顺性和开启轻便性指标进行分析.基于台架开展滑移门测试，验证了该建模仿真分析有较高的精度.

2）提出滑移门运动机构，尤其是导轨结构的参数化设计方法，显著提升了试验设计的效率.根据大量样本点数据进行灵敏度分析，找到了滑移门平顺性和开启轻便性的主要影响因素.

3）结合二阶响应面方法与NSGA-II遗传算法，对滑移门系统的动力学特性进行多目标优化.优化后，关闭过程中的中导向轮载荷峰值及质心加速度峰值分别降低39%和24.4%，且开启所需时间低于1.8 s，在满足开启轻便性要求的情况下，显著提升了滑移门的运动平顺性.

4）由于制造试验样件的成本较高，未对优化后的滑移门运动机构方案进行试验验证.该滑移门动力学特性多目标优化方法的效果将在后续新MPV车型的开发过程中进行验证.

参考文献

[1]    MUNEER M，SHARMA Y. Study of sliding door closing speed for a manually operated sliding door[C]// SAE 2015 World Congress & Exhibition.Detroit： SAE international，2015-01-1318.

[2]    SUZUKI S，FUKUMOTO R，OHHASHI M，et al. Development of power sliding door（PSD）system with push-pull cable driving method[C]// SAE 2000 World Congress.Detroit： SAE international，2000-01-0080.

[3]    刘鹏飞，王义柏，郑辉，等.车用滑移门系统多体运动动力学分析建模[J].机电一体化，2013，19（5）：18—22 ，61.

LIU P F，WANG Y B，ZHENG H，et al. Kinematic and dynamic modeling and analysis of automobile sliding door[J]. Mechatronics，2013，19（5）：18—22，61.（In Chinese）

[4]    蒋东升，杜国省，李永生，等.基于Adams/View的汽车滑移门动力学仿真分析[J].计算机辅助工程，2013，22（S1）：8—10，20.

JIANG D S，DU G X，LI Y S，et al. Dynamic simulation analysis on automotive sliding door based on Adams/View [J]. Computer Aided Engineering，2013，22（S1）：8—10，20.（In Chinese）

[5]    廖鸿胡，赵云飞，成艾国，等.基于正交试验的汽车滑移门平顺性优化研究[J].机电工程，2010，27（12）：49—52.

LIAO H H，ZHAO Y F，CHENG A G，et al. Optimization on ride performance of automotive sliding door based on orthogonal experiments[J]. Journal of Mechanical & Electrical Engineering，2010，27（12）：49—52.（In Chinese）

[6]    高云凯，马干干，杜倩倩.滑移门系统刚柔耦合多体动力学特性研究[J].汽车技术，2016（9）：1—3，8.

GAO Y K，MA G G，DU Q Q. A study on dynamic characteristics of sliding door system based on rigid-flexible coupling multi-body model[J]. Automobile Technology，2016（9）：1—3，8.（In Chinese）

[7]    LI Y J，GAO Y K，MA G G，et al. A study on optimization of the ride comfort of the sliding door based on rigid-flexible coupling multi-body model[C]// SAE World Congress Experience.Detroit： SAE International，2017-01-0417.

[8]    周长江，胡波，祝智斌.某型包装机推手机构刚柔耦合系统动力学研究[J].湖南大學学报（自然科学版），2014，41（5）：39-43.

ZHOU C J，HU B，ZHU Z B. Dynamic study of pusher device system with rigid-flexible coupling in packing machine [J]. Journal of Hunan University（Natural Sciences）， 2014， 41（5）： 39—43. （In Chinese）

[9]    周五峰，陈梓铭，缪利锋，等.基于缓和曲线曲率修正的中滑门平顺性提升[C]//2016中国汽车工程学会年会论文集.北京：中国汽车工程学会，2016：1463—1465.

ZHOU W F，CHEN Z M，MIU L F，et al. Optimization for the smoothness of automobile sliding door based on curvature modification with transition curve [C]// 2016 SAE-China Congress Proceedings. Beijing： SAE-China，2016： 1463—1465.（In Chinese）

[10]  刘鹏飞.汽车滑移门系统的运动学和多刚体动力学建模与参数优化[D].上海：上海交通大学机械与动力工程学院，2013：36—40.

LIU P F. Multi-rigid-body kinematic and dynamic modeling and optimization of sliding door[D]. Shanghai： School of Mechanical Engineering，Shanghai Jiao Tong University，2013：36—40.（In Chinese）

[11]  程军圣，余.基于响应面法的听小骨消声器的优化设计[J].湖南大学学报（自然科学版），2017，44（2）：60—65.

CHENG J S，YU H. Optimal design of ossicular silencer based on response surface methodology [J]. Journal of Hunan University （Natural Sciences），2017，44（2）：60—65.（In Chinese）