曲面结构的表面电荷反演计算方法

杜志叶　易凡　金颀　邹建明　姚勇

摘  要：研究高压直流输电线路下绝缘材料表面电荷积聚与消散规律时，只能根据绝缘材料表面静电电位反演计算得到电荷密度，但当材料表面为曲面时，很难准确计算出材料表面电荷密度.提出了一种针对曲面的电荷密度反演计算方法，针对曲面的绝缘材料，合理、密集地选择电位测量点，通过多轴运动控制器得到电位测量点的相对位置坐标，再按测量点将曲面划分为三角形的网格，求出各点处的法向量，进而反演出表面电荷密度.测量得到的3D打印的曲面圆盘和悬式绝缘子表面电位，以此为算例计算其表面电荷密度.计算结果同理论分析趋势一致，绝缘材料表面的静电电位与电荷密度相关性较强，电位高的区域对应的电荷密度也大;电荷分布按照离放电电极距离的远近，呈现“同心圆”分布;但靠近悬式绝缘子钢帽的区域电荷难以积聚，电荷密度小.

关键词：曲面电荷反演计算;绝缘子;表面电位;振荡Kelvin探头

中图分类号：TM851                               文献标志码：A

Surface Charge Inversion Calculation Method for Curved Surface Structures

DU Zhiye1，YI Fan1，2，JIN Qi1，ZOU Jianming3，YAO Yong3

（1.School of Electrical Engineering and Automation，Wuhan University，Wuhan 430072，China;

2. Wuhan Metro Group Co Ltd，Wuhan 430017，China;

3. Central China Branch of State Grid Corporation，Wuhan 430075，China）

Abstract： When studying the surface charge accumulation and dissipation law of insulating materials under HVDC transmission lines，the charge density can only be calculated by surface electrostatic potential inversion of insulating materials. However it is difficult to accurately calculate the surface charge density when the insulating material surface is curved. In this paper，a charge density inversion method for curved surface was proposed. The potential measurement points were selected reasonably and intensively，and then curved surface was divided into triangular meshes according to the selected measurement points. The normal vectors at each point were obtained，and the surface charge density was then inverted. As an example，the surface potential of 3D printed curved surface and suspended insulator was measured，and the surface charge density was calculated. The calculated results are in accordance with the theoretical analysis trend. The electrostatic potential of insulating material surface has a strong correlation with the charge density，and the charge density corresponding to the high potential area is also large. The charge density presents a“concentric circle” distribution according to the distance from the discharge electrode，but the charge near the suspended insulator cap is difficult to accumulate，and the charge density is small.

Key words： surface charge inversion calculation;insulator;surface potential;oscillating Kelvin probe

高压直流输电线路运行时，电晕产生的空间电荷在电场力的作用下会作定向运动，影响线路下方的电场分布[1-2].电晕电荷积聚到电气设备绝缘表面，如绝缘子、直流分压器等设备的绝缘伞裙表面，使得绝缘表面的电位分布和沿面電场发生畸变，引发闪络等严重后果[3].随着电压等级的提升，特别是特高压直流输电工程，电晕电荷对电气设备外绝缘性能的影响不容忽视.近年来，国内清华大学、重庆大学、西安交通大学等在绝缘材料电荷积聚问题方面进行了大量试验研究[4-9]，但要研究绝缘材料表面电荷积聚与消散规律，就必须准确定量计算出绝缘材料表面电荷密度分布.

目前，常见的绝缘材料表面电荷密度测量方法主要有3种，分别为：粉尘图法[10]、电容探头法[11]以及基于普尔克斯（Pockels）效应的光学测量方法[12].其中，粉尘图法只能对表面电荷进行定性的测量分析，无法得到其具体的数值.基于普尔克斯（Pockels）效应的光学测量方法只能针对一些透明的绝缘薄膜材料，而电力系统中电气设备绝缘表面使用的绝缘材料大多数都是不透明的.所以，目前国内外学者在对绝缘材料表面电荷进行试验测量研究时，都采用电容探头法先对表面电位进行测量，再利用静电场理论，计算反演得到绝缘材料表面电荷密度.

在20世纪90年代，日本学者Ootera等人[13]在研究绝缘子表面电荷的积聚分布规律时，提出了利用表面视在电荷法将试验测得的绝缘子表面电位转换为表面电荷，也即进行电荷反演计算.随后，清华大学对电荷反演方法进行了简化[14]，但是面对复杂的曲面结构，在不知道曲面具体尺寸时，依旧不能精确计算出其表面电荷密度.

本文基于振荡Kelvin探头测量的电位结果[15]，提出一种能计算任意曲面尺寸的电荷反演方法，通过合理的网格划分，计算出复杂曲面的电荷密度.

1   电荷反演方法简介

通过振荡Kelvin探头测量得到了绝缘表面的电位分布，为了进一步得到绝缘表面的电荷分布，采用表面电荷反演计算方法，将试验得到的电位值转换为电荷密度值.

视在电荷法认为：在电晕放电之后，绝缘子表面存在着极化电荷和自由电荷，根据叠加定理，空间中任意一点P的电位φ（P）和电场强度E（P）都由这两种电荷在该点产生的电位和电场强度叠加形成.因此，引入绝缘表面视在电荷密度的概念：

σa = σ + σ′   （1）

式中：σ为自由电荷密度;σ′为极化电荷密度.则点P的电位和电场强度的积分表达式分别为[16]：

式（2）～式（3）中：ε0为真空中的介电常数;r为点P到空间中任意一点的距离;S为空间中的所有表面.

根据有限元的思想，将绝缘表面划分成n个网格，当网格数n足够大的时候，可以认为每个网格内的电荷均匀分布，此时对于每个单元网格，其电位和电场强度的表达式可以进一步改写成如下

形式：

由式（4）便可以得到绝缘表面视在电荷密度与绝缘表面电位之间的矩阵方程如下：

定义电位系数矩阵P如下：

则可以求得绝缘表面各个单元的表面视在电荷密度为：

对于任意一个单元格，其自由电荷密度的计算表达式为：

式中：ε1和ε2分别指绝缘材料和空气的介电常数;Ei1和Ei2分别为交界面处绝缘表面和空气表面的场强;ni为第i个单元格由分界面指向空气侧的单位法向量.

可以认为Ei2和Ei1大小相等，而Ei2的数值可由式（5）计算得到，将其代入式（9）则可以得到关于自由电荷密度σ和视在电荷密度σa的矩阵表达式：

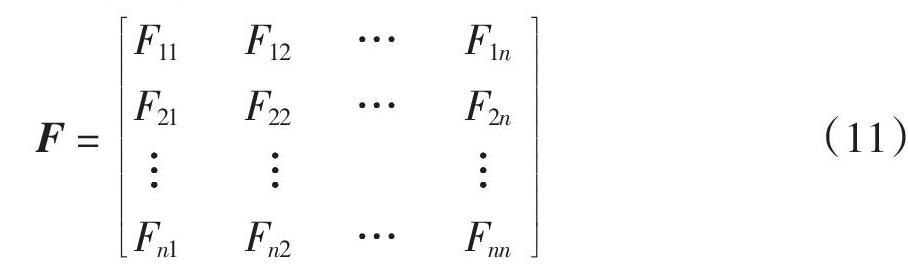
定义矩阵F如下：

矩阵F中的每个元素的计算表达式如（12）所示.

在式（7）中，电位系数矩阵P的每个元素可由式（2）计算得到，但涉及到积分过程，计算过程较为复杂，因此本文对其进行如下处理.

当i≠j时，Pij的积分表达式如下：

式中：rij为第i个点到第j个单元的距离.当网格的划分足够密的时候，两个单元格之间任意两点的距离相差很小，因此可以使用2个单元格中心之间的距离来代替在积分过程中变化很微弱的rij.此时式（13）可以简化为式（14）.

式中：Si为第i个网格单元的面积.当i=j时，会使得rij→0，此时式（14）不再成立，无法使用其计算Pij.将第i个网格单元的Si等效为半径Ri的圆盘，并带有均匀的视在电荷面密度σ（a），其中Ri可由下式计算得到：

由于圆盘和原网格的面积相等，因此沿圆盘的轴线z方向上任意一点的电位可以表达为：

式中：z0为沿轴线方向上任意一点与圆盘的垂直距离.为了计算紧挨网格表面的电位，令z0→0，计算式（16）的极限可得

因此，当i=j时，Pij的计算表达式为

由式（14）和式（18）可以得到，绝缘表面视在电荷与表面电位之间的电位系数矩阵P的任意一个元素计算表达式如下

2   曲面结构电荷反演计算

2.1   曲面电荷反演和平面的区别

根据上一节介绍的反演计算原理可知，平面与曲面材料进行反演计算时，主要存在两点区别：

1）平面材料在进行表面网格划分时，所有单元位于同一平面上，因此可以简化为二维模型，只需用x和y两个坐标即可表示每个单元的位置;而曲面材料进行单元划分后则需要用x、y、z这3个坐标才能表示出每个单元的位置.

2）在计算时，式（12）表达形式不一样.具体而言，当i≠j时，对于平面材料Fij=0;而对于曲面材料，则需要计算出对于整个曲面各个单元中心点处单位法向量nk，然后算出两个向量rik和nk之间的夹角;将rik和nk之间的夹角记为θ，在实际的电荷密度计算过程中，Fij表达式可以简化成如下形式：

2.2   曲面表面电荷密度反演方法

由2.1节可知，曲面和平面在进行电荷反演计算时，主要区别就在于表面法向量的计算.平面向量的乘积为0;曲面由于面上各點处的法向量互不相同，向量乘积不为0，需要求解出面上各点处的法向量.

对于已知其曲面方程的曲面结构，在求解各点的法向量时，可以直接通过曲面方程求导获得，但在实际的工程中，测量绝缘子等未知其表面曲面方程的试品时，曲面方程求导的方法无法适用.因此，应当选取一种适用于所有曲面结构的通用求解方法.

根据空间几何，3点确定一个平面，如图1所示，△ABC是曲面试品表面进行网格划分之后的一个网格，由于网格划分很小，认为每个网格所在区域内为平面，点A、B、C为该网格的3个顶点，O为该网格的中心点，n为该网格所在平面的法向量（当网格划分为四边形或者多边形时，只需选取3个顶点用于计算即可）.A、B、C三点的坐标可由具体的网格划分获得，当A、B、C的坐标分别为A（x1，y1，z1），

根据相关空间几何可知：

因此，反演计算方法式（23）中的第一项可以用已知坐标数据写成如下形式：

式中：Si為该网格的面积;r1、r2和r3分别为向量rij的3个坐标;rij为向量rij的模长.对于确定的网格划分，每个网格面积Si都已确定且已知，向量rij的坐标也可以通过每个网格的中心坐标求得.因此，式（24）中的量都已知，可以直接求出Fij的值.

3   算   例

3.1   表面电位测量平台

搭建试验测量平台来测量绝缘材料表面静电电位，如图2所示.该系统由高压部分和低压部分组成，高压部分包括负极性直流电压发生器、调压器、电极支架、球电极和板电极构成，低压部分由有源静电探头、传动机构、运动控制系统、静电电位计、数据采集卡及计算机等构成[17].

ig.2   Schematic diagram of measurement test platform

试验测量平台中，试品放置在金属圆盘上，金属圆盘可以自由旋转.球电极放置在试品的几何中心位置，通过给球电极加压让其产生电晕，使球电极下的试品表面积聚电荷.运动控制系统由步进电机、步进电机驱动器以及多轴运动控制器组成，可编程精确控制有源静电探头的位置，实现对整个试品全表面电位的测量.通过多轴运动控制器上显示的相对坐标可以知道每一个电位测量点相对于探头起点的位置，通过换算可以得出每个电位测量点相对于金属圆盘中点的坐标.电位测量点合理、密集的分布，就可以覆盖整个绝缘材料表面，知道每个测量点的电位值和对应的坐标，再按测量点将曲面划分为三角形的网格，求出各点处的法向量，进而反演出表面电荷密度.有源静电探头与静电电位计相连，通过数据采集卡将采集到的电位信号输入至计算机，由LabVIEW平台自动保存测量结果.

试验过程中，使用步进电机控制静电探头的仰角，使探头始终与被测曲面保持垂直，探头距离绝缘材料表面距离为0.5～1 cm.由于试验中使用的是有源静电探头，探头通过内置电压源反馈得到绝缘材料表面电位值，在测量范围内，测量结果不受探头到绝缘材料距离影响.在试验平台中，球电极的半径为1 cm，试验中的金属圆盘和试验的金属桌可靠接地，模拟实际工况.

3.2   3D打印的曲面圆盘表面电荷反演计算

采用3D打印技术，制作了表面带有一定曲率的伞形绝缘圆盘，其直径均为20 cm，最大厚度为2 cm，圆盘截面取的是一个圆弧，截面示意图如图3所示.将截面绕旋转轴旋转一周，即可形成一个上表面为曲面的圆盘，曲面圆盘的实物图如图4所示.

采用3D打印技术，能精确地控制曲面圆盘表面的形状，这为电荷反演计算时的网格剖分、坐标计算等提供了精确的坐标数据.

试验中，球电极放置在曲面圆盘的几何中心位置，球电极加压60 kV产生电晕，球电极放电结束后测量曲面圆盘表面静电电位.选择静电探头测量点，探头的测量轨迹从远离圆盘的位置移动到圆盘中心，测量完第一圈电位后向圆盘边缘移动1 cm，再次测第二圈圆周上的表面电位，如此循环直至移动到圆盘边缘.从中心到边缘一共有10个圆周，每个圆周上测点数分别为4个、10个、16个、16个、16个、20个、20个、20个、24个、24个，共计170个测点，扫描整个圆盘共需要7 min.静电探头的运动轨迹如图5（a）所示，有限元网格划分如图5（b）所示.

以曲面圆盘的中心为原点，建立三维直角坐标系，由几何关系可计算出每一个测量点的X、Y、Z坐标，测得的圆盘表面静电电位如图6所示.根据上文的曲面电荷密度反演方法，计算得到曲面圆盘表面的电荷密度如图7所示.

观察圆盘表面电位分布以及电荷密度的分布，可以发现：静电电位与电荷密度相关性较强，静电电位高的区域电荷密度会比静电电位低的区域大;绝缘曲面圆盘表面电荷分布趋势为中心电荷密度大，边缘电荷密度小，且沿着径向由中心向边缘递减.由于试验中电极和曲面圆盘呈现轴对称分布，电荷密度的分布也近似呈现出轴对称的特征，电荷密度大小按照离球电极的距离近似呈现“同心圆”的分布.

3.3   悬式绝缘子表面电荷密度反演计算

以工程中常见的悬式绝缘子为例，反演计算绝缘子表面电荷密度[18].选择涂PRTV涂料的XHP-

210陶瓷悬式绝缘子，绝缘子公称直径为170 mm，结构高度为300 mm，其外表面形状无法用曲线来拟合，绝缘子表面电位测量平台如图8所示.在试验平台中，球电极加压50 kV，放电持续3 min，球电极距离绝缘子钢帽距离为5 cm.球电极放电结束后，测量绝缘子表面静电电位，用上述方法来反演计算绝缘子表面电荷密度.

从外向里测量绝缘子表面电位，每一圈测量点之间的间距是相等的，一共测量7圈，每一圈都选择24个点，每一圈的位置示意图如图9（a）所示，探头的运动轨迹如图9（b）所示.

通过多轴运动控制器得到每一个电位测量点的坐标，测量得到绝缘子表面电位如图10所示.试验过程中测量到绝缘子钢帽上静电电位为0，在反演时可以认为钢帽部分没有积聚电荷，直接镂空绝缘子钢帽部分.根据上文的曲面电荷密度反演的方法，计算绝缘子表面电荷密度如图11所示.

由图10和图11可知，绝缘子中心钢帽的存在很大程度地影响了绝缘子表面电荷的积聚.由于钢帽的存在，靠近绝缘子钢帽的区域电荷难以积累，对应区域电荷密度低.绝缘子表面电荷分布并不是越靠近球电极电荷密度越高，反而是绝缘子中间部分电荷密度最大，喷涂PRTV涂料的绝缘子表面电荷积聚时，电荷密度的峰值约为-1.2 μC/m2.

4   结   论

本文提出一种计算曲面电荷密度反演算法，通过多轴运动控制器显示的相对坐标，合理、密集地选择电位分布點，能计算出曲面表面的电荷密度.

1）提出将曲面划分为三角形网格的方法，利用向量乘积的形式求出面上各点处的法向量，求出F矩阵，进而反演得到曲面电荷密度.

2）通过多轴运动控制器上显示的相对坐标，结合合理、密集的选择电位测量点，可以知道覆盖整个绝缘材料表面的电位测量点的电位值和对应的坐标值，能反演出曲面材料表面电荷密度，从而能定量研究各种形状绝缘材料表面电荷积聚与消散规律，指导高压直流条件下绝缘设计.

3）以3D打印的曲面圆盘和悬式绝缘子为算例，能通过其表面测量的电位值，反演计算出表面电荷密度，其中喷涂了PRTV涂料绝缘子表面电荷密度的峰值约为-1.2 μC/m2.

参考文献

[1]    DU Z Y，HUANG G D，RUAN J J，et al. Calculation of the ionized field around the DC voltage divider [J]. IEEE Transactions on Magnetics，2013，49（5）：1933—1936.

[2]    HUANG G D，RUAN J J，DU Z Y，et al. Highly stable upwind FEM for solving ionized field of HVDC transmission line [J]. IEEE Transactions on Magnetics，2012，48（2）：719—722.

[3]    舒印彪. 中国直流输电的现状及展望[J]. 高电压技术，2004，30（11）： 1—2.

SHU Y B. Present status and prospect of hvdc transmission in china [J]. High Voltage Technology，2004，30（11）： 1—2.（In Chinese）

[4]    王强，张贵新，王新新. 直流电压下气固交界面表面电荷积聚现象的实验分析[J]. 高电压技术，2011，37（3）： 594—598.

WANG Q，ZHANG G X，WANG X X. Surface charge accumulation phenomenon at the gas-solid interface under dc voltage [J]. High Voltage Technology，2011，37（3）： 594—598.（In Chinese）

[5]    王邸博，唐炬，刘凯.直流高压下GIS支柱绝缘子表面电荷积聚特性[J].高电压技术，2015，41（9）：3073—3081.

WANG D B，TANG J，LIU K. Charge accumulation on post insulator surface under HVDC in GIS [J]. High Voltage Technology，2015，41（9）： 3073—3081.（In Chinese）

[6]    张贵新，张博雅，王强，等. 高压直流GIL中盆式绝缘子表面电荷积聚与消散的实验研究[J]. 高电压技术， 2015，41（5）： 1430—1436.

ZHANG G X，ZHANG B Y，WANG Q，et al. Experiment study of surface charge accumulation and decay on a cone-type insulator in HVDC GIL [J].High Voltage Technology，2015，41（5）： 1430—1436. （In Chinese）

[7]    张博雅，王强，祁■，等. 直流电压下聚合物表面电荷测量方法及积聚特性[J]. 中国电机工程学报，2016，36（24）： 6664—6676.

ZHANG B Y，WANG Q，QI Z，et al. Measurement method and accumulation characteristics of surface charge distribution on polymeric material under DC voltage [J]. Chinese Journal of Electrical Engineering，2016，36 （24）： 6664—6676.（In Chinese）

[8]    高文强，张博雅，张贵新. 硅橡胶材料表面电荷消散现象[J]. 高电压技术，2017，43（2）： 468—475.

GAO W Q，ZHANG B Y，ZHANG G X. Surface charge dissipation of silicone rubber materials [J]. High Voltage Technology，2017，43（2）： 468—475.（In Chinese）

[9]    王蓓，张贵新，王强，等. SF6及空气中绝缘子表面电荷的消散过程分析[J]. 高电压技术，2011，37（1）： 99—103.

WANG B，ZHANG G X，WANG Q，et al. Analysis of surface charge decay process on insulators in SF6 and air [J].High Voltage Technology，2011，37（1）：99—103.（In Chinese）

[10]  HAMA H，HIKOSAKA T，OKABE S，et al. Cross-equipment study on charging phenomena of solid insulators in high voltage equipment [J]. IEEE Transactions on Dielectrics & Electrical Insulation，2007，14（2）： 508—519.

[11]  PEDERSEN A .On the electrostatics of probe measurements of surface charge densites [J]. Gaseous Dielectrics V，1987：235—241.

[12]  王友功，川崎俊之，高田達雄. 普克尔斯效应反射法测量绝缘膜表面放电电荷的分布[J]. 西安交通大学学报，1996，30（11）：53—59.

WANG Y G，KAWASAKI J，TAKADA T. Puckers effect reflection method for measuring the distribution of discharge charge on the surface of insulation films [J]. Journal of Xi'an Jiaotong University，1996，30 （11）： 53—59.（In Chinese）

[13]  OOTERA H，NAKANISHI K. Analytical method for evaluating surface charge distribution on a dielectric from capacitive probe measurement-application to a cone-type spacer in ±500 kV DC-GIS [J]. IEEE Transactions on Power Delivery，1988，3（1）： 87—89.

[14]  付洋洋，王强，张贵新，等. 基于表面电位测量的表面电荷反演计算[J]. 高电压技术，2013，39（1）： 88-95.

FU Y Y，WANG Q，ZHANG G X，et al. Inverse calculation of surface charge based on surface potential measurement [J].High Voltage Technology，2013，39（1）：88—95.（In Chinese）

[15]  王力伟，杜翠薇，刘智勇，等. 扫描Kelvin探针的电化学原理分析[J]. 腐蚀科学与防护技术，2013，25（4）： 327—330.

WANG L W，DU C W，LIU Z Y，et al. Analysis of electrochemical principle of scanning Kelvin probe [J]. Corrosion Science and Protection Technology，2013，25 （4）： 327—330.（In Chinese）

[16]  倪光正，杨仕友，钱秀英，等. 工程电磁场数值计算[M]. 北京： 机械工业出版社，2006：209-211.

NI G Z，YANG S Y，QIAN X Y，et al. Engineering electromagnetic field numerical calculation [M]. Beijing： Machinery Industry Press，2006：209-211.（In Chinese）

[17]  WANG Q，ZHANG G，WANG X. Characteristics and mechanisms of surface charge accumulation on a cone-type insulator under DC voltage [J]. IEEE Transactions on Dielectrics and Electrical Insulation，2012，19（19）：150—155.

[18]  ZHANG B，ZHANG G，WANG Q，et al. Suppression of surface charge accumulation on A12O3-filled epoxy resin insulator under DC voltage by direct fluorination [J]. AIP Advances，2015，5（12）： 127207-1—127207-12.