基于空间笛卡尔坐标系转换的三轴一体光纤陀螺标定数学建模*

赵桂玲,姜雨含,李 松

(辽宁工程技术大学测绘与地理科学学院, 辽宁阜新 123000)

0 引言

光纤陀螺(fiber optic gyroscope,FOG)以其启动时间短、动态范围大、抗冲击、寿命长、测量精度高等优点在捷联惯性导航系统(strap-down inertial navigation system,SINS)中得到快速发展和广泛应用[1-2]。作为捷联惯性导航系统的核心部件,光纤陀螺标定精度直接影响惯性导航系统的工作精度[3-4]。光纤陀螺标定精度取决于三轴一体光纤陀螺标定数学模型精度以及基于数学模型的标定路径设计与参数估计方法。国内外对光纤陀螺标定技术的研究主要集中在:利用惯性测试转台提供的速率和位置进行分立式标定[5]；利用Kalman滤波技术进行标定参数估计的系统级标定方法[6-9]；利用GPS、磁传感器、光电成像系统等提供的外界辅助信息进行在线标定[10-12]。无论哪类载体、哪种方法进行光纤陀螺标定,都是在假设光纤陀螺标定模型固定已知的前提下进行理论推导和实验,鲜有对标定模型本身精确性、可靠性及适用性的分析,部分探讨与研究也只是分析具体参数对固定模型的影响[13],缺乏对模型严格准确的推导,而标定模型在一定程度上决定了标定方法的选择和标定参数误差分配,并对系统性能评估具有重要的指导意义。

如果光纤陀螺标定模型过于简化,参数估计简单,工程易于实现,但不能满足系统精度的要求；如果将所有认知的模型参数都考虑在内,又会给实验室标定或系统在线标定带来困难,况且有些系数在激励不够的情况可以忽略。针对以上关键工程应用问题,从光纤陀螺标定模型的物理意义出发,以光纤陀螺坐标系相对载体坐标系之间的安装误差角为切入点,提出基于空间笛卡尔坐标系转换矩阵的三轴一体光纤陀螺标定数学建模方法,建立3种工程常用的光纤陀螺标定线性数学模型,并给出模型中各个参数的物理意义和模型的适用条件。最后通过仿真和一套光纤陀螺捷联惯性导航系统标定与导航试验结果对3种模型进行比较和分析。

1 数学建模

文中从三轴一体光纤陀螺的工程安装结构出发,兼顾惯性导航系统补偿精度和标定试验难度,对三轴一体光纤陀螺进行数学建模。

1.1 单轴光纤陀螺数学模型

由于光纤陀螺具有标度因数线性度好、动态和静态误差小等优点[14],一般情况下单轴光纤陀螺标定常采用线性输入输出模型。光纤陀螺没有与g和g2相关的误差项,且忽略随机误差的影响,单轴光纤陀螺脉冲输出与角速率之间的转换模型为:

Ng=Kgωg+D0

(1)

式中:Ng为光纤陀螺脉冲输出;ωg为光纤陀螺输入角速率;Kg为光纤陀螺标度因数;D0为光纤陀螺零偏。

1.2 空间笛卡尔坐标系变换

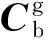
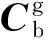
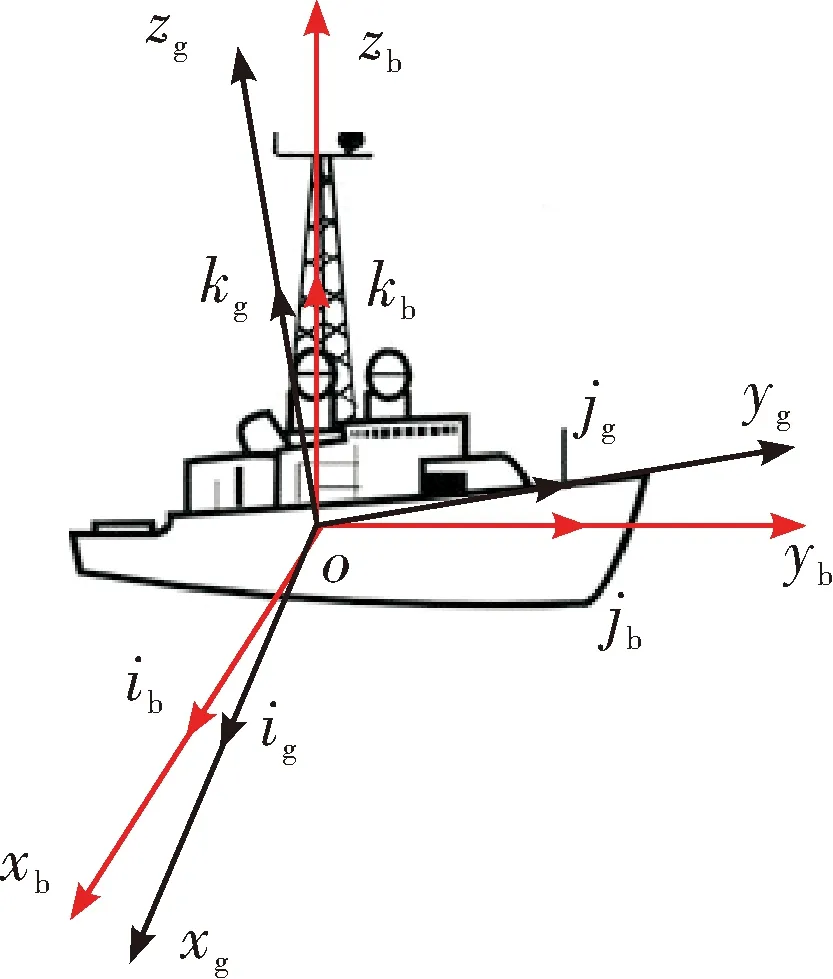
图1 两坐标系安装示意图

根据空间笛卡尔坐标系基变换公式,可得b系到g系的基变换公式:

(2)

b系到g系的坐标变换矩阵:

(3)

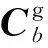
2)式(3)是在3个光纤陀螺任意安装下求得的坐标系变换矩阵,一般情况下,g系3个轴与b系对应轴在空间笛卡坐标系内成小角度安装,此时:

(4)

式(3)可简化为:

(5)

3)式(5)是式(3)下的一种特例与简化,更进一步,假设g系3个轴与b系对应轴在空间笛卡坐标系内不但成小角度安装,且g系3个轴正交安装,即g系构成空间笛卡尔直角坐标系,则:

cosθmgnb=-cosθngmb;m≠n;m,n=i,j,k

(6)

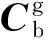
(7)

此时,b系到g系的坐标系变换,也可以通过图2的3次旋转实现。

图2 b系到g系的坐标系旋转

将3次旋转表述成3个独立的方向余弦阵,b系到g系的变换用3个独立的方向余弦阵乘积表示。

(8)

当旋转角ψ、θ、φ为小角度时,对式(8)进行化简,并忽略二阶以上小量,可得:

(9)

对标定而言,式(7)和式(9)具有相同的表现形式,但两矩阵元素Cij(i≠j)表达的物理意义却不同,对于小角度转动,

(10)

1.3 三轴一体光纤陀螺数学模型

三轴一体光纤陀螺是一种将惯性导航所需3个正交方向的陀螺设计成一体化的光纤陀螺,根据单轴光纤陀螺数字量与角速率之间的转换模型,将三轴一体光纤陀螺模型写成矢量形式:

Ng=Kgwg+D0

(11)

式中:

(12)

式中：wg是角速率矢量在陀螺坐标系g系下的投影,而惯性导航解算需要的是角速率矢量在载体坐标系b系下的投影wb,由于安装误差的存在,wb与wg之间存在如下关系:

(13)

将式(13)代入式(11),可得三轴一体光纤陀螺静态输入输出标定数学模型为:

(14)

(15)

(16)

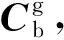
2 六位置光纤陀螺标定

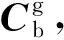
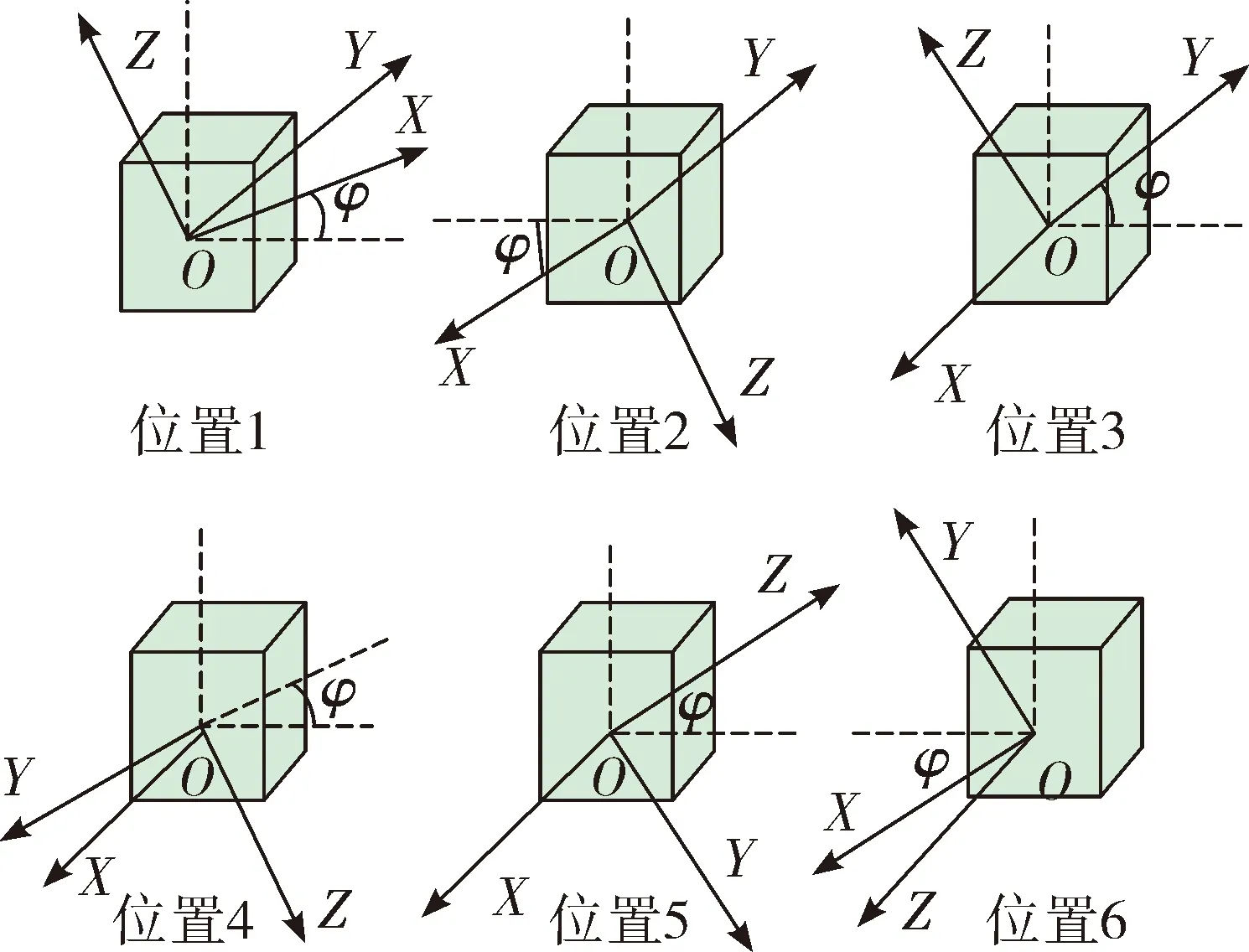
图3 光纤陀螺标定路径设计

(17)

根据6个位置的光纤陀螺脉冲输出,可以计算出三轴一体光纤陀螺标定数学模型参数:

(18)

(19)

(20)

将式(19)～式(20)计算出的标定模型参数代入式(16),则可以根据任意的光纤陀螺脉冲输出计算光纤陀螺的输入角速率wb。

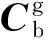
(21)

(22)

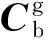
(23)

3 仿真及实验分析

3.1 计算机仿真

采用六位置标定方法对三轴一体光纤陀螺进行标定,忽略转台定位误差、加速度计误差、初始对准误差等对系统的影响,在静止条件下分析光纤陀螺简化模型标定数学模型对系统的影响。仿真条件如下:

简化的光纤陀螺标定数学模型对姿态、速度、位置的影响如图4～图9所示:

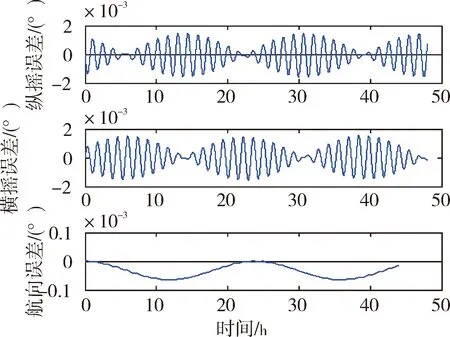
图4 3个安装误差角简化模型对姿态的影响

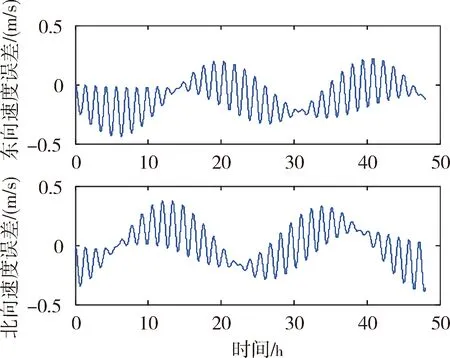
图5 3个安装误差角简化模型对速度的影响

图6 3个安装误差角简化模型对位置的影响

从仿真图可以看出:在0.1o随机安装误差条件下,简化的三轴一体光纤陀螺标定数学模型引起捷联惯性导航系统速度误差、位置误差和姿态误差。简化为3个安装误差角形式的标定数学模型引起的系统导航误差大于6个安装误差角形式的标定数学模型引起的系统导航误差。两种简化形式的标定数学模型均引起随时间增长的位置误差。

3.2 转台实验

将光纤陀螺捷联惯性导航系统置于三轴惯性测试转台,转台角位置精度3 ″。控制转台按照图3设计的光纤陀螺标定路径进行旋转,每个位置停留2 min,采集光纤陀螺输出,按照式(17)～式(23)分别对3种数学模型进行参数分解,并将计算结果代入捷联惯性导航系统进行导航解算,导航结果如图10所示。

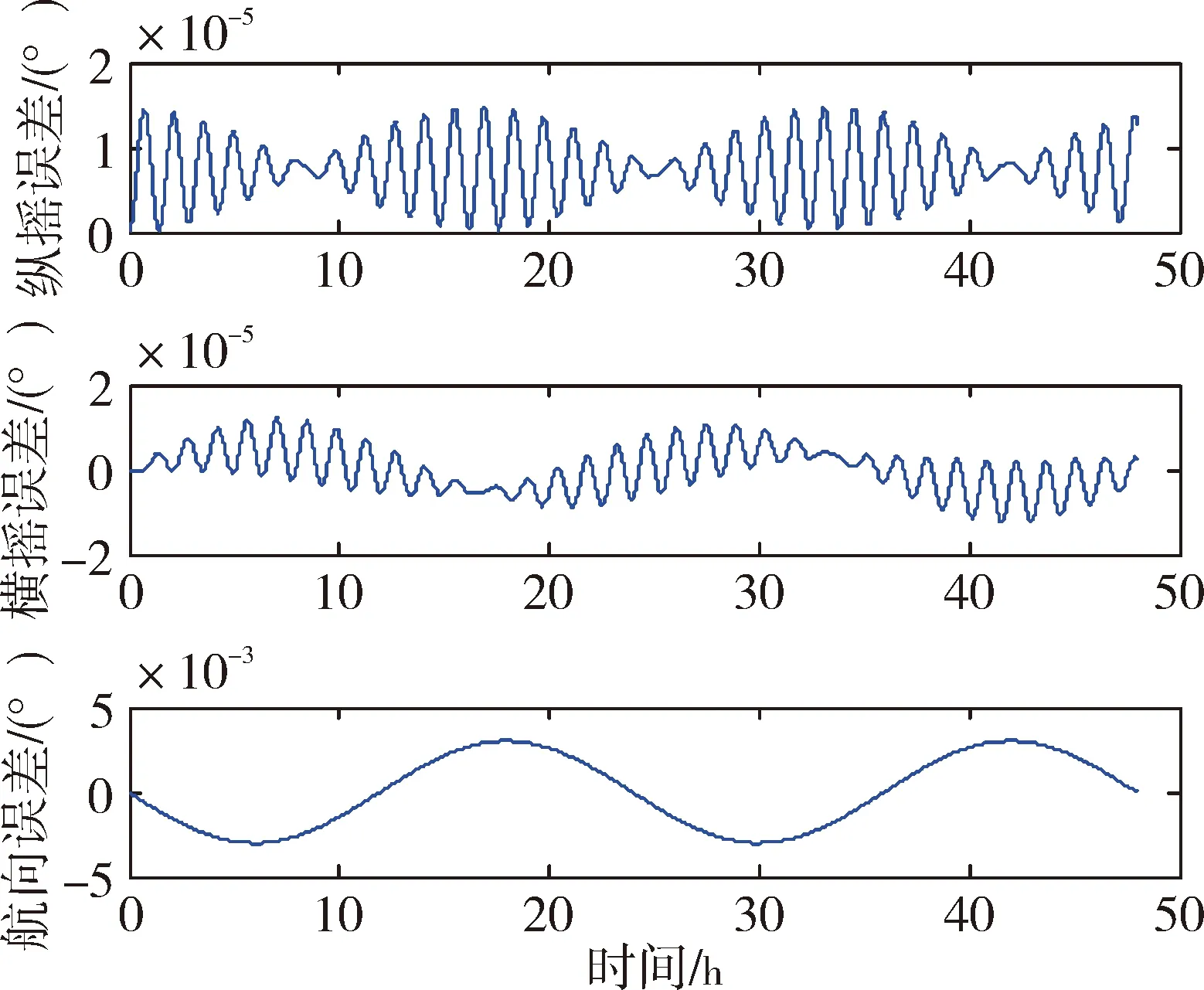
图7 6个安装误差角简化模型对姿态的影响

图8 6个安装误差角简化模型对速度的影响

图9 6个安装误差角简化模型对位置的影响

三轴一体光纤陀螺标定数学模型采用的安装误差角为9个、6个和3个时,静态导航定位误差分别为4.15 nmile/40 h、6.02 n mile/40 h合20.21 n mile/40 h。3个安装误差角形式的光纤陀螺标定数学模型引起的定位误差远大于6个安装误差角形式的标定模型和9个安装误差角形式的标定模型引起的定位结果。实验误差大于仿真结果,这是因为在标定实验和导航实验中,不可避免的会存在加速度计误差、转台定位误差、初始对准误差等,这些都对导航结果产生一定的影响。

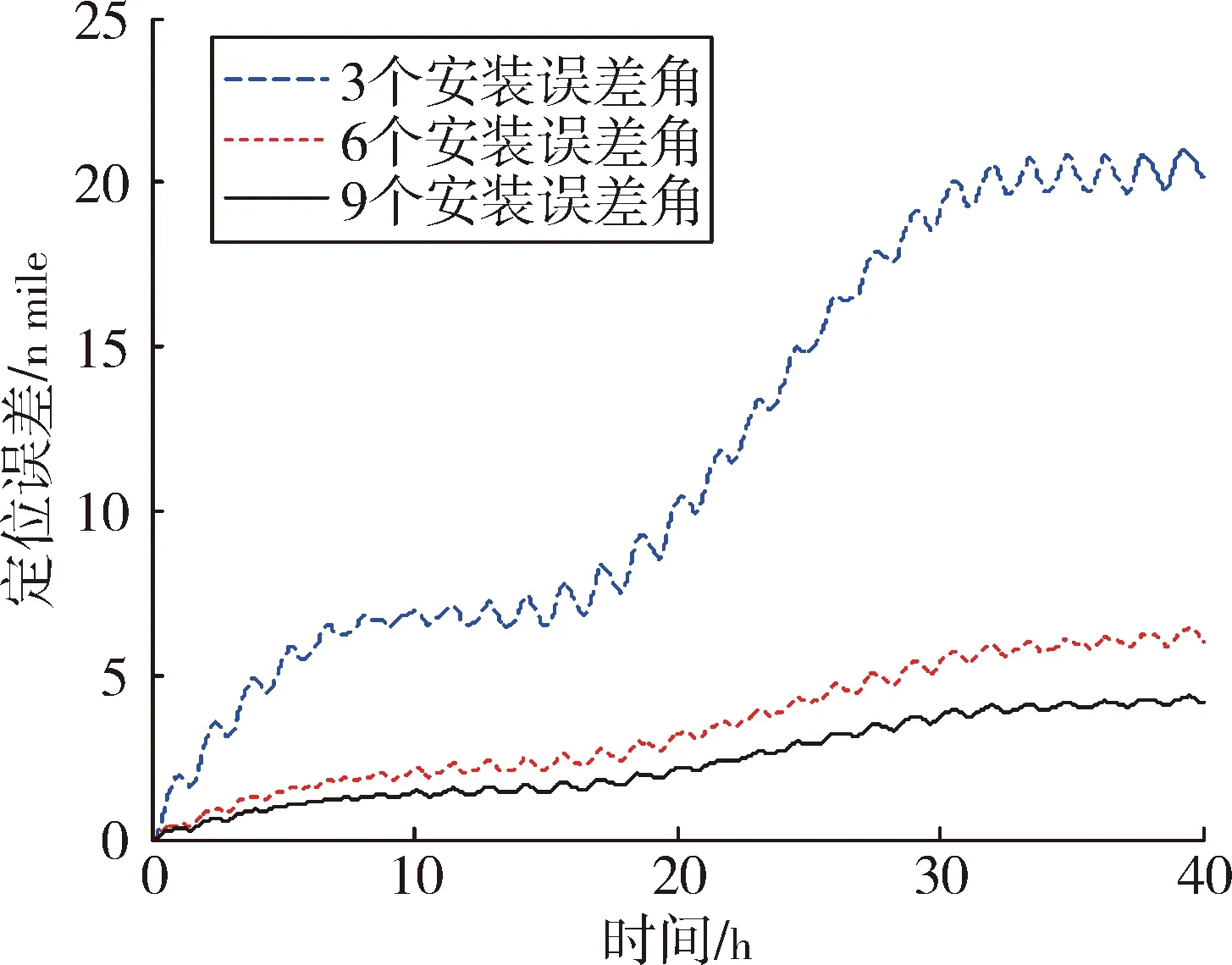
图10 导航定位误差

4 结论

文中提出一种基于空间笛卡尔坐标系转换矩阵的三轴一体光纤陀螺标定数学建模方法,建立了3种光纤陀螺标定数学模型,给出模型中各个参数的物理意义,并通过六位置标定方法对3种数学模型中的参数进行标定。计算机仿真及实验结果表明:简化的光纤陀螺标定数学模型对系统速度、位置、和姿态都有影响,影响的大小与光纤陀螺标定误差模型参数有关,模型参数越多,模型越精确,引起的导航误差越小,越能满足精度要求。