紧邻高边坡道路基坑土压力的能量法分析

张家林　张可能　陈骏　左文贵　王彦之　贺勇　金福喜

摘要：基于能量法原理，明确场地斜坡不利作用下紧邻边坡进行基坑开挖时的主动土压力，并提出一种适用于紧邻边坡条件下的基坑土压力计算模型，通过数学推导，得出主、被动土压力计算公式。同时，以郴州某公路基坑工程为例，采用能量法原理以及数值模拟分别计算土压力，对比计算结果，检验能量法计算公式的准确性。研究结果表明：两种方法边坡各位置的主动土压力计算结果差距在5%以内，被动土压力计算结果一致;数值模拟结果较于能量法结果偏小，最大误差不超过10%，表明该计算公式基本正确;同时，研究表明坡高和倾角的增加均使得主、被动土压力增大，被动土压力较主动土压力受边坡倾角的影响更为明显。

关键词：道路工程;计算模型;能量法;主动土压力;边坡参数

中图分类号：U417文献标识码：A文章编号：1006-8023（2019）03-0078-09

Analysis of Earth Pressure on Foundation Pit Adjacent

to High Slope by Energy Method

ZHANG Jialin1，2， ZHANG Keneng1，2*， CHEN Jun3， ZUO Wengui1，2， WANG Yanzhi1，2，HE Yong1，2， JIN Fuxi1，2

（1.Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring，

Ministry of Education， Changsha， 410083; 2.School of Geoscience and Infophysics， Central South University，

Changsha， 410083; 3.China Construction Fifth Bureau Civil Engineering Co.， Ltd.， Changsha 410083）

Abstract：Based on the principle of energy method， this paper defines the active earth pressure when the foundation pit is excavated next to the slope under the adverse effect of the site slope， and puts forward a model for calculating the earth pressure of the foundation pit next to the slope. Through mathematical deduction， formulas for calculating active and passive earth pressure are obtained. Taking a highway foundation pit project in Chen Zhou as an example， the results of earth pressure is calculated and compared by energy method and numerical simulation respectively to verify the accuracy of the formula of energy method. The results show that the difference between the two methods is less than 5%， and the results of passive earth pressure are consistent. The result of numerical simulation is smaller than that of energy method， and the maximum error is less than 10%. At the same time， the research shows that the passive earth pressure increases with the increase of slope height and inclination. And the passive earth pressure is more obviously affected by the slope inclination than the active earth pressure.

Keywords：Road engineering; calculation model; energy method; active earth pressure; slope parameters

0引言

緊邻边坡条件下进行基坑开挖是各类基坑工程乃至岩土工程中的一类典型问题。在此情况下，边坡荷载对基坑的影响对基坑工程的设计和施工提出了更高的要求，边坡或基坑的问题，直接影响相邻结构的受力情况。国内外学者[1-5]针对基坑和边坡之间的影响做出许多研究。其中，大部分针对计算土压力修正系数展开。由于边坡的旁压作用对基坑侧壁的影响，侧壁土压力的计算需要更加精确才能衡量边坡所带来的影响。尽管在土压力计算理论的发展过程中也获得了许多的成果，也比较了计算方法和计算模型的精确性[6-15]，但针对紧邻边坡基坑的土压力研究并不多见，传统的朗肯、库仑土压力理论在这种复杂条件下的无法满足计算的精确度。

本文基于能量法[16-22]理论，对已有的数学模型进行扩展延伸并引入边坡参数，研究边坡荷载对基坑侧壁土压力的影响。并基于工程实例利用能量法计算主动土压力，将计算结果与有限元模拟结果以及传统的朗肯法、库伦法结果对比，发现该方法能够较为准确地计算紧邻高边坡时基坑侧壁土压力。

1能量法理论推导

1.1能量法计算土压力原理

能量理论在土压力计算中的运用是建立在库仑理论的基础上。在极限平衡状态下，土体不但要满足应力场中力的平衡条件与强度条件，还需要满足速度场中的能量守恒定理。在对真实工况进行土压力计算时，通常要考虑动荷载与静荷载两种作用。

土在进入流塑状态时，满足米塞斯提出的流动法则[23]。通过流动法则的分析，流塑状态土体中，土体内摩擦角余切的相反数为剪应变速率与发向应变速率之比。土体在流塑过程中伴随着体积的膨胀。从微观角度看，存在宽dx、高dy的单元土体，在竖向应力σn作用下达到塑性流动状态时，土体表面各点产生剪切速度和竖直方向的变形速度，分别为：νdy-εndy=tgφνdy。水平剪切速度和竖向变形速度的矢量和为应变速度矢量ν，与受剪面夹角为β，如图1所示。

根据图1中几何关系，有：

tg β=εnν。（1）

根据流动法则，有：

tgβ=εnν=tg φ。（2）

因此有：

β=φ。（3）

公式（3）表明，土处于流塑状态时，滑动面上任意一点处应变速度矢量ν与该点处滑动线夹角呈φ。

土体在塑流中的能量变形在剪应力作用下所做的功为：

τ·ν=cν+σntg φ·ν。（4）

将产生的体积膨胀所吸收的功σnεn代入公式（4），有：

σnεn=σntg φν。（5）

因此单位土体消耗的能量为：

N=τ·ν-σntg φν=cν=c·νcos φ。（6）

式中：v 为剪切面上的应变速率。

1.2计算模型构建和土压力方程推导

1.2.1计算模型构建

由于经典土压力计算理论的局限性，本文提出一种新的计算紧邻边坡条件下基坑侧壁土压力的计算方法。

建立基坑达到主动状态时的计算模型（图2），AB为假设的挡土墙墙面，垂直高度为H，墙面与竖向夹角为ε，与土体摩擦角为δ。墙后边坡坡角为η，垂直高度为h。坡后土体向上倾斜并无限延伸，倾斜面与水平面夹角为θ。假定滑动面为直线BD，与水平方向夹角为α，土体单层且均匀，并在图2中构建如下的几何关系：过A点作辅助线AC∥ED交BD于C点;过E作辅助线EG⊥AC，垂足为G;过C作辅助线CF⊥DE，垂足为F，最后连接EC。

几何关系构建后不规则四边形土体ABDE重量即分为△ABC、△AEC、△ECD三部分，可得出土重W的表达式为：

W=W△ABC+W△AEC+W△EDC

=12γH2cos（ε-θ）cos（α-ε）cos2εsinα-θ+hHcos-ε-αsinη-θsinηcosεsinα-θ+h·sinη-θsinη·

hsinη-θsinηtanα-θ+Hsin90+ε-αcosεsinα-θ-hsinη-θsinηtanη-θ。（7）

1.2.2主动土压力方程推导

主动土压力的方向与挡墙面法线夹角为δ。土体处于流塑状态时，面BD上方滑动土体的速率为ν，方向与BD面夹角为φ。作用在滑动土体上的外力为重力W与挡墙对土体反力Pa，模型中重力及土体反力做功之和等于假定滑动面处所消耗的能量，即：

N=NW+NPaH+NPaV=M。（8）

重力可由公式（7）计算，因W作用方向与v竖直分量的方向一致，故W做功为正。土压力Pa在计算过程中可以分为两块处理，其竖直分量和水平分量分别为Pasinε+δ与Pacosε+δ，按照土压力分量计算各自方向做的功NPaH与NPaV。由于Pa水平分量与竖直分量方向皆与υ相反，故相应所做的功为：

NPaH=-Pacosε+δ·υcos（α-φ）。（9）

NPaV=-Pasinε+δ·υsin（α-φ）。（10）

外力所做功为以上几者之和，整理可得公式（11）。

内力做功主要表现形式为土体在滑动面BD上滑动所产生的能量损耗，可按摩擦理论来进行求解，如公式（12）所示。

N=NW+NPaH+NPaV=12γυsin（α-φ）H2cos（ε-θ）cos（α-ε）cos2εsinα-θ+hHcos-ε-αsinη-θsinηcosεsinα-θ+

h·sinη-θsinη·hsinη-θsinηtanα-θ+Hsin90+ε-αcosεsinα-θ-hsinη-θsinηtanη-θ-Pacosε+δ·υcos（α-φ）-Pasinε+δ·υsin（α-φ）。（11）

M=cυcosφ·BC+CD=cυcosφ·Hsin（90+θ-ε）cosεsin（α-θ）+hsin（η-θ）sinηsin（α-θ）。（12）

根據能量守恒建立平衡关系，有：

12γυsin（α-φ）H2cos（ε-θ）cos（α-ε）cos2εsinα-θ+hHcos-ε-αsinη-θsinηcosεsinα-θ+h·sinη-θsinη·

hsinη-θsinηtanα-θ+Hsin90+ε-αcosεsinα-θ-hsinη-θsinηtanη-θ-Pacosε+δ·υcosα-φ-

Pasinε+δ·υsinα-φ=cυcosφ·Hsin（90+θ-ε）cosεsin（α-θ）+hsin（η-θ）sinηsin（α-θ）。（13）

消去公式中速率υ，得：

Pa=12γH2sin（α-φ）cos（ε-θ）cos（α-ε）cos2εsinα-θcosε+δ-α+φ+12γhHsin（α-φ）cos-ε-αsinη-θsinηcosεsinα-θcosε+δ-α+φ+

12γh2sin（α-φ）sinη-θsinη·hsinη-θsinηtanα-θ+Hcos（ε-α）hcosεsinα-θ-hsinη-θsinηtanη-θcosε+δ-α+φ-

ccosφ·Hcos（θ-ε）cosεsin（α-θ）+hsin（η-θ）sinηsin（α-θ）cosε+δ-α+φ。（14）

整理得：

Pa=12γH2Ka1+hHKa2+h2Ka3-Ka4。（15）

其中：

Ka1=sinα-φcos（ε-θ）cos（α-ε）cos2εsinα-θcosε+δ-α+φ。

Ka2=sinα-φcos-ε-αsinη-θsinηcosεsinα-θcosε+δ-α+φ。

Ka3=sin（α-φ）sinη-θsinη·hsinη-θsinηtanα-θ+Hcos（ε-α）hcosεsinα-θ-hsinη-θsinηtanη-θcosε+δ-α+φ。

Ka4=ccosφ·Hcos（θ-ε）cosεsin（α-θ）+hsin（η-θ）sinηsin（α-θ）cosε+δ-α+φ。

此時在满足能量守恒的条件下，方程中仅有α未知。之后可依据极值条件，求出Pa的最大值，得到主动土压力的计算结果。

1.2.3被动土压力方程推导

被动土压力的计算与主动土压力计算的原理类似，主要区别在于被动土压力Pp的大小和作用方向与主动土压力不同，被动土压力计算时假设土体滑动方向（即应变速率υ的方向）与主动土压力不同。因此对主动土压力的计算模型进行调整，如图2所示。此时滑动土体四边形ABDE的重力W与主动土压力相同，可按主动土压力求解方法进行计算。而外力做功的计算上与主动土压力的不同之处在于一些力做功正负的变化。具体为应变速率的竖直方向分量与重力方向相反，重力做负功;应变速率水平方向分量、竖直方向分量分别与被动土压力水平方向分量Ppcos（ε-δ）、Ppsin（ε-δ）相同和相反，因此分别做正功和负功。推导过程如下：

Pp=12γH2sinα+φcosε-θcosα-εcos2εsinα-θcosε-δ+α+φ+12γhHsinα+φcos-ε-αsinη-θsinηcosεsinα-θcosε-δ+α+φ+

12γh2sinα+φ·sinη-θsinη·hsinη-θsinηtanα-θ+Hcosε-αhcosεsinα-θ-hsinη-θsinηtanη-θcosε-δ+α+φ+

ccosφ·Hcosθ-εcosεsinα-θ+hsinη-θsinηsinα-θcosε-δ+α+φ=12γH2Kp1+hHKp2+h2Kp3+Kp4。（16）

其中：

Kp1=sinα+φcos（ε-θ）cos（α-ε）cos2εsinα-θcosε-δ+α+φ。

Kp2=sinα+φcos-ε-αsinη-θsinηcosεsinα-θcosε-δ+α+φ。

Kp3=sinα+φ·sinη-θsinη·hsinη-θsinηtanα-θ+Hcos（ε-α）hcosεsinα-θ-hsinη-θsinηtanη-θcosε-δ+α+φ。

Kp4=ccosφ·Hcos（θ-ε）cosεsin（α-θ）+hsin（η-θ）sinηsin（α-θ）cosε-δ+α+φ。

同理，满足能量守恒的条件下式中仅有α未知，通过导数为0来求出Pp的最大值，得到被动土压力的计算结果。

2能量法计算紧邻边坡的基坑侧壁主动土压力的应用

2.1工程概况

湖南省某公路基坑工程位于郴州市城东郊，基坑长约97 m，东西宽约45 m，最大深度约为12 m，工程面临基坑开挖的问题。场地平面示意图如图3所示，基坑右侧匝道b设计位置将经过原边坡坡脚，边坡高度约为37 m。同时，在下穿匝道a设计位置紧邻场地西南侧山体边坡，坡高约为21 m。由于场地地形起伏特点及煤系地层的不良条件，需结合排水设施的修筑以保证基坑开挖过程中的稳定性。

2.2能量法计算土压力的特解

朗肯及库仑土压力理论在土压力计算过程中不能很好地处理边坡荷载的影响，因此在边坡高度为0 m的特殊条件下传统理论计算土压力才较为准确。为了印证能量法计算主动土压力的合理性，通过取h与η同时为最小值时，能够满足能量法和库伦土压力的假设条件相同，从而得到能量法计算主动土压力结果的特解。将此时的计算结果与传统的土压力计算理论进行对比，可以反映出各种计算方式的差异。假设在边坡高度h = 0 m时运用三种理论计算主动土压力，假定墙高H = 11 m;土体采用砂土，重度γ=19 kN/m3，摩擦角φ=20°，墙背摩擦角δ=0°，几何条件为墙面与竖直方向夹角ε=15°。边坡后无限延伸土体水平。参数α为土压力极限值确定的滑动面与水平面夹角，由公式（11）计算得到夹角值α= 34.731°。

不同计算方法的结果见表1。结果表明推导所得能量法计算结果介于朗肯、库仑土压力理论所得主动土压力计算结果之间。经典土压力理论中，朗肯法计算主动土压力较实际偏大[19]，而库仑土压力计算结果也会有2%～10%的偏差。因此能量法介于两者之间的结果可以较为真实的反映实际主动土压力的大小。被动土压力结果的对比反映出能量法的计算值与朗肯法结果相近，三种方法计算的差异较小故具有较高的可信性。

2.3能量法计算结果与数值模拟结果比较

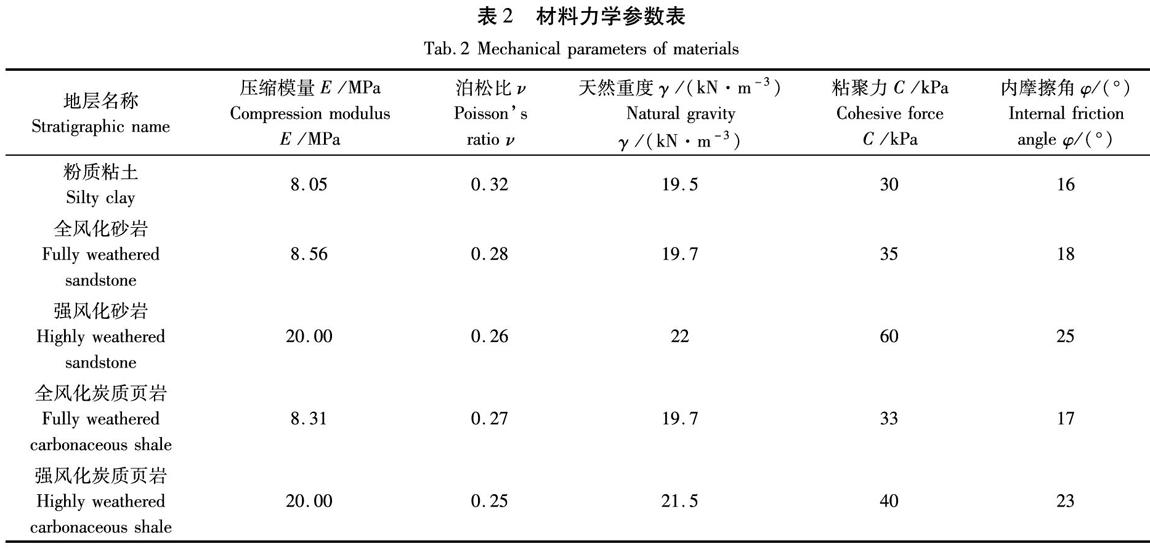
根据上文所推得的主动土压力计算公式，选取西南侧基坑侧壁与高边坡相邻最近处为计算截面，计算不同开挖深度下基坑侧壁的主动土压力，工程概况如上所述，具体模型参数见表2。采用Midas有限元模拟软件对开挖过程进行模拟网络划分示意图如图4所示。数值模型采用标准边界条件，即假设模型右侧无水平位移，底部固定约束，顶部则为自由边界。为方便计算，地层重度等数据选取勘察报告中各地层数据的加权平均值。其中能量法计算结果见表3。

根据上述步骤得出了基坑侧壁在不通开挖深度下的主动土压力结果，圖5表示用有限元方法和能量法计算的结果对比。结果显示当开挖深度小于1.1 m时，模拟结果相对于能量法公式计算结果偏小，随着开挖深度的增加，能量法公式计算结果相对于数值模拟结果所得曲线较为平缓;在-4 m深度下，模拟结果相对于能量法结果偏小;在-4 ～ 8 m段差距较大，但最大误差不超过10%。因此在整体开挖深度下，能量法计算结果具有高度的可信性，将其运用到紧邻边坡的基坑主动土压力计算中能够得到合理的结果。

3边坡几何参数对基坑土压力影响分析

能量法计算得到的紧邻边坡下基坑主动土压力结果与模拟结果有着很好的契合，但在实际计算中，还需要研究模型与公式中边坡几何参数影响。

选取边坡几何参数——倾角η与坡高h，探索两者的值对基坑土压力的作用规律。研究模型以上述工程案例为基础建立，通过Python软件呈现不同几何参数对基坑侧壁土压力的影响和规律。土体指标选取基坑工程中场地土参数，假设条件中除墙背摩擦角δ=35°、粘聚力c=35 kPa外，其他参数与2.2节中一致。边坡后无限延伸土体倾角θ=12°。边坡竖直高度h取0 m至10 m不等。受几何关系限制，边坡倾角需大于土体倾角，即η≥tan-1（hHtanε+H+htanα）。因此当h<5.77 m时η最小值为η=θ;当5.77

根据图6和图7显示的主、被动土压力随边坡参数的变化关系。图中颜色由浅到深表示土压力数值逐渐增大。沿主动土压力轴（z轴）正向提升曲线对曲面进行切割，图像颜色由蓝变红表示土压力逐渐增加。可见基坑主动土压力受坡高和坡脚的影响变化十分显著，且主动土压力随着坡角和坡高的增大而增大，被动土压力也表现出相同的变化趋势。坡高从0 m增加至10 m，主动土压力由855 kPa增至1 780 kPa，而被动土压力增幅要大于主动土压力的增幅。这是由于边坡高度的增加引起紧邻基坑边坡土体的增多，土体增多引起的边坡重度增大间接地增加了基坑侧壁的旁压，变化趋势符合一般规律。

压缩h轴后，边坡倾角η与主动土压力关系如图8所示。倾角在0.25 rad至0.6 rad之间时，随着倾角的增加，主动土压力增加极为明显。倾角超过0.6 rad时，主动土压力增加幅度减小，几乎呈线性增加。因此主动土压力在一定范围内受边坡坡角的影响较为显著。对被动土压力而言，其变化趋势也呈现出对数增长趋势，在0.2～0.4 rad阶段增长较快，后逐渐进入稳定增长状态，倾角大于一定弧度后增长趋势不再明显。

在相同的假设条件下将计算后的基坑的主、被动土压力结果与两个不同的几何因素置于同一坐标系下观察，如图9所示。对比发现主、被动土压力在变化趋势方面反映出了一致性，即坡高和倾角的增加均使得主、被动土压力产生增加效果。但被动土压力较主动土压力受边坡倾角的影响更为明显，尤以0.2 ～ 0.4 rad段最为明显。

4结论

（1）能量法原理创建的紧邻边坡条件下的基坑土压力计算模型，推导出主、被动土压力的计算公式，适合分析解决工程问题。

（2）能量法计算土压力得到的特解与传统土压力计算方法所得结果进行对比，发现能量法计算主动土压力的值介于朗肯法与库仑法之间，更接近于库仑土压力，而对于被动土压力，三者的值十分接近。

（3）通过能量法计算结果与有限元模拟结果的对比，发现两者除了在个别区段有少许差异外，整体结果十分接近。边坡坡高、坡角对基坑的土压力计算的影响程度不同。

（4）坡高与基坑主动土压力呈大致线性关系，与被动土压力呈高度线性关系。坡角的增大对主动土压力和被动土压力的影响均表现出了先趋于对数后趋于线性的增长趋势，即坡度在0.25～0.6 rad时，土压力增幅较大，之后其呈现出线性增长趋势。两者对比反映出土压力对坡脚更为敏感，且被动土压力的受影响程度大于主动土压力的受影响程度。

【参考文献】

[1]孙凯，方宗新，苏魁聪. 高陡边坡下基坑边坡的稳定与变形控制设计[C]. 中国岩石力学与工程学会第七次学术大会论文集，西安： 2002.

SUN K， FANG Z X， SU K C. Stability and deformation control design of foundation pit slope under high and steep slope[C].

The Seventh Conference Proceedings of the China Society of Rock Mechanics and Engineering， Xian， China， 2002.

[2]刘继强，田志强，林志斌，等. 高边坡对邻近基坑稳定性的影响研究[J]. 隧道建设， 2011，31（3）：294-300.

LIU J Q， TIAN Z Q， LIN Z B， et al. Influence of high slope on stability of adjacent foundation pits[J]. Tunnel Construction， 2011， 31（3）： 294-300.

[3] HWANG Y S， LEE S D. The earth pressure on the rigid wall depending on the separation distance during the adjacent ground excavation[J]. International Journal of Geo-Engineering， 2015， 6（1）： 3.

[4]许美. 基坑设计中将既有边坡作为等效荷载处理的合理性研究[J]. 中国水运， 2017，39（9）： 40-42.

XU M. Research on rationality of treating existing slope as equivalent load in foundation pit design[J]. China Water Transport， 2017， 39（9）： 40-42.

[5]张菊连，沈明荣. 福建高速公路边坡岩土体质量评价方法[J].哈尔滨工业大学学报，2011，43（10）：113-118.

ZHANG J L， SHEN M S. Fujian highway slope rock mass quality evaluation method[J]. Journal of Harbin Institute of Technology， 2011， 43（10）： 113-118.

[6]姚国圣. 考虑位移的土压力计算方法在基坑工程中的应用[J]. 岩土工程学报， 2013，31（S2）： 693-696.

YAO G S. Application of earth pressure calculation method considering displacement in foundation pit engineering[J]. Chinese Journal of Geotechnical Engineering， 2013， 31（S2）： 693-696.

[7]鄧子胜，邹银生，王贻荪. 考虑位移非线性影响的深基坑土压力计算模型研究[J]. 工程力学， 2004，21（1）： 107-111.

DENG Z S， ZOU Y S， WANG Y S. Study on soil pressure calculation model of deep foundation pit with nonlinear displacement effect[J]. Engineering Mechanics， 2004， 21（1）： 107-111.

[8]徐日庆. 考虑位移和时间的土压力计算方法[J]. 浙江大学学报（工学版）， 2000，34（4）： 370.

XU R Q. Calculation method of earth pressure considering displacement and time[J]. Journal of Zhejiang University （Engineering Science）， 2000， 34（4）： 370.

[9]孙玉永，周顺华，庄丽. 考虑残余应力的基坑被动区土压力及强度计算[J]. 土木工程学报， 2011，44（9）：94-99.

SUN Y Y， ZHOU S H， ZHUANG L. Calculation of soil pressure and strength in passive area of foundation pit considering residual stress[J]. China Civil Engineering Journal， 2011， 44（9）： 94-99.

[10]金亚兵，刘吉波. 基坑支护设计中的若干问题探讨[J]. 岩石力学与工程学报， 2009，28（S2）：3844-3849.

JIN Y B， LIU J B. Discussion on some problems in foundation pit support design[J]. Chinese Journal of Rock Mechanics and Engineering 2009， 28（S2）： 3844-3849.

[11]王文杰，曾进群，陈小丹.深基坑开挖中有限土体土压力计算方法探讨[J].矿产勘查，2005，18（3）：30-31.

WANG W J， ZENG J Q， CHEN X D. Discussion on the calculation method of soil pressure of finite soil mass in deep foundation pit excavation[J]. Mineral Exploration， 2005， 18（3）： 30-31.

[12]王洪亮，宋二祥，宋福渊. 紧邻既有建筑基坑有限土体主动土压力计算方法[J]. 工程力学， 2014，31（4）： 76-81.

WANG H L， SONG E X， SONG F Y. Calculation method of active soil pressure of finite soil mass adjacent to existing foundation pits[J]. Engineering Mechanics， 2014， 31（4）： 76-81.

[13]白琦，肖明. 基于能量法的地下隧洞动静力稳定性分析[J].工程科学与技术，2018，50（3）：247-255.

BAI Q， XIAO M. Dynamic and static stability analysis of underground tunnel based on energy method[J]. Advanced Engineering Sciences， 2008， 50（3）： 247-255.

[14]张可心，孙全胜.拉索损伤对斜拉桥静力性能影响分析[J].公路工程，2016，41（3）：35-39.

ZHANG K X， ZHANG Q S. The impact analysis of cable damage on the static performance of cable-stayed bridge[J]. Highway Engineering， 2016， 41（3）： 35-39.

[15]李玉飞，叶义成，胡南燕，等. 基于能量法的露天开采下采空区顶板安全厚度研究[J].金属矿山，2018，43（2）：35-40.

LI Y F， YE Y C， HU N Y， et al. Research on safety thickness of goaf roof under open pit mining based on energy law[J]. Metal Mine， 2018， 43（2）： 35-40.

[16]李辉. 大型基坑支护体系计算模型的分析与比较[D]. 上海：同济大学， 2007.

LI H. Analysis and comparison of calculation model of large foundation pit support system[D]. Shanghai： Tongji University， 2007.

[17]刘成清，倪向勇，杨万理，等. 基于能量法的被动柔性棚洞防护结构设计理论[J].工程力学，2016，33（11）：95-104.

LIU C Q， NI X G， YANG W L， et al. Design theory of passive flexible shelter structure based on energy method[J]. Engineering Mechanics， 2016， 33（11）： 95-104.

[18]蒋峻峰，姚顺忠，吴永红. 深大基坑空间内支撑结构整体受力性能研究[J]. 森林工程， 2013， 29（4）：124-127.

JIANG J F， YAO S Z， WU Y H. Research on the overall mechanical performance of supporting structure in deep and large foundation pit space[J]. Forest Engineering， 2013， 29（4）：124-127.

[19]赵康，鄢化彪，冯萧，等. 基于能量法的矿柱稳定性分析[J].力学学报，2016，48（4）：976-983.

ZHAO K， YAN H B， FENG X， et al. Stability analysis of pillar based on energy method[J]. Chinese Journal of Theoretical and Applied Mechanics， 2016， 48（4）： 976-983.

[20]刘胜来，李全旺. 从数学推导过程讨论能量法的适用条件[J].力学与实践，2014，36（4）：497-499.

LIU S L， LI Q W. Discussion on the applicable conditions of energy method from the mathematical derivation process[J]. Mechanics in Engineering， 2014， 36（4）： 497-499.

[21]文芬. 基于能量理论的挡土墙土压力计算分析与研究[D]. 长沙：长沙理工大学， 2008.

WEN F. Calculation， analysis and research on earth pressure of retaining wall based on energy theory[D]. Changsha： Changsha University of Science and Technology， 2008.

[22]顾慰慈. 挡土墙土压力计算手册[M]. 北京：中国建材工业出版社， 2005.

GU W C. Calculation manual of earth pressure of retaining wall[M]. Beijing： China Building Materials Industry Press， 2005.

[23]姚仰平. 土力學[M] .北京：高等教育出版社，2001.

YAO Y P. Soil mechanics[M]. Beijing： Higher Education Press， 2001.