学情分析与教学预设

李珍

在日常教学过程中，我们有时会遇到这样的情况：备课时感觉学习内容比较简单，但在课堂教学中却意外频出，倍感煎熬。这正是我最近上《分桃子》，即商是两位数的笔算除法的真实感受。

我的备课思考

北师大版三年级下册第一单元的笔算除法，是在列竖式计算表内除法和两位数除以一位数商是两位数的口算基础上进行教学的。本课时就是把两位数除以一位数商是两位数的口算用列竖式的方式计算。学生已经会口算68÷2，笔算68÷2和口算的计算过程完全一样，只是要书写成竖式的形式罢了。需要注意的是，以前学生写的竖式都是一步计算，而今天的竖式是两步计算，仅此而已。

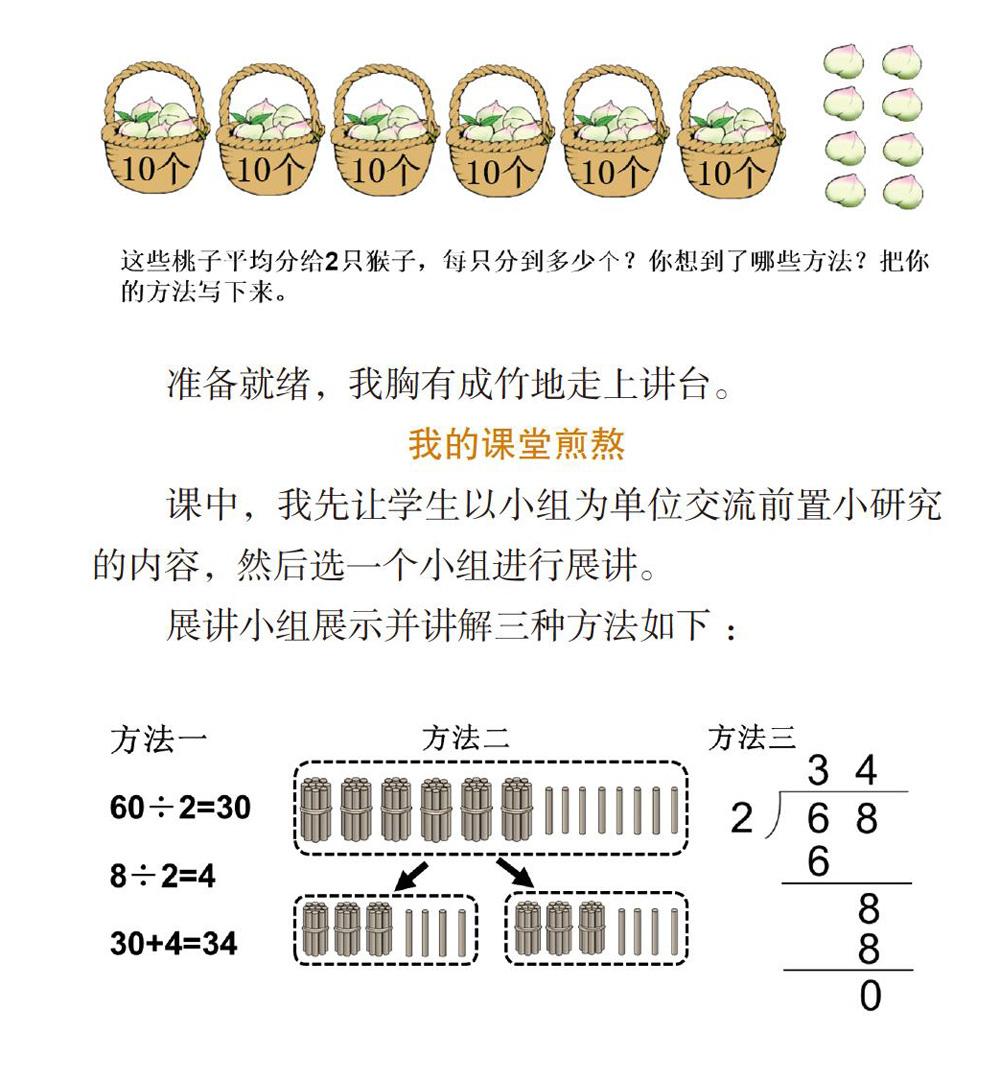
基于以上考虑，我把例题设计成前置小研究（如下图），让学生在家里完成。

准备就绪，我胸有成竹地走上讲台。

我的课堂煎熬

课中，我先让学生以小组为单位交流前置小研究的内容，然后选一个小组进行展讲。

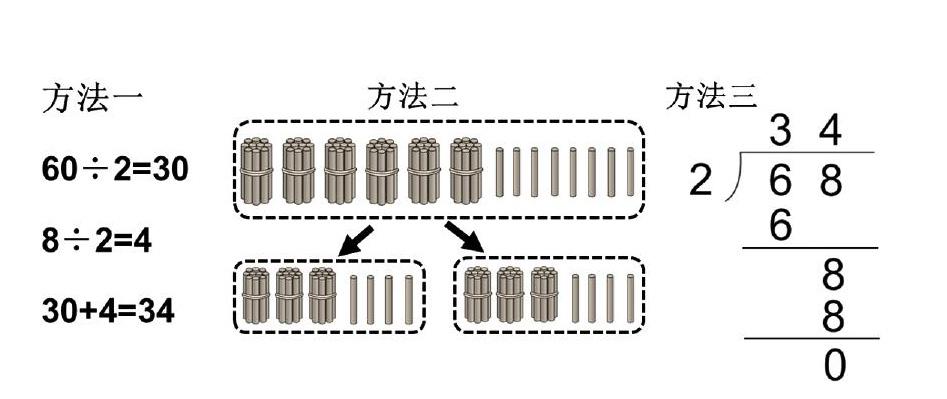
展讲小组展示并讲解三种方法如下：

展讲生：哪位同学对我们的方法有疑问？

质疑生A：我对你们的竖式有疑问，以前的除法竖式都是一条横线（等于号），今天这个竖式怎么是两条横线？

展讲生：因为我们是先算 60÷2=30，然后再算 8÷2=4，所以是两条横线。

生A 懵懵懂懂地坐下，不太理解，但不知从何问起。

质疑生B：以前竖式的商是一位数，今天为什么是两位数？

展讲生：因为 60÷2=30， 8÷2=4，30+4=34。所以商是两位数。

显然学生的回答并没有触及到竖式的核心，所以老师介入。

师：第二种方法，先分的是谁？（60根），然后呢？（又分 8 根），因为分了两次，所以商是两位数。

展讲生：谁还有补充？

下面的学生小手如林。

一学生上台补充（如右图）：

下面的学生：我也是……我也是……认同之声不绝于耳。

真是大写的尴尬，原本以为学生会否定，结果学生好像都非常赞同。

无奈之下，我再次强调：比较一下这两种竖式，你更喜欢哪一种？

生C：我喜欢方法四，因为它比较简单。

师：那其他同学呢？

仅有少数几个同学举手。

生D：我喜欢方法三，因为它能清楚地看出我们是怎么分的。

我仿佛抓到了救命的稻草：就像这位同学说的，这样的竖式能清楚地看明白我们分小棒的过程。下面请同学们把这个竖式在练习本上写一遍。

学生在自己的练习本上写了一遍，又在我的要求下同桌之间互相说了说是怎么算的。

我觉得学生已经理解得差不多了，就让学生试做：96÷3。

结果让人大跌眼镜，情况如下：

更有学生向我提出：“老师，明明口算可以很快得出结果，为什么要用这么麻烦的竖式，不用竖式行不行？”

面对学生的提问我哭笑不得……

后续的情况，大家也可以想到，我极其痛苦与艰难地“说服”学生用标准竖式，并反复强调竖式书写的格式和顺序，但收效甚微，此时下课铃声已然响起，只好草草收场。

很显然，原本以为很简单的课，让我给上砸了。

我的课后反思

回顾整个教学过程，显然教师没有理解学生的困惑是两部分，一部分是这道除法竖式为什么是两条横线，另一部分是商为什么是两位数。所以无论是学生的解釋还是教师的介入都是无效的，如果教师引导学生理解了以上两个问题，就不会出现学生补充的错误例子了。这充分说明了教师充分准备的重要性，更说明课堂学习进程中教师要随时把准学生误入歧途的原因，才能对症下药，有效设置思维训练点和思维激活点，才能把教学推入高潮。

诚然，由于教师的备课不到位，没有对学情深入分析，只是一味地用“标准竖式”否定学生，所以才会把一节课上得“苦不堪言”，这节课的学习质量因此降低了。由此可见，教师在课堂教学质量的保障方面起着多么重要的作用。

所以，从学生认知需要出发对课堂主体部分进行改进，在另一班执教时取得了良好的效果。

我的课堂再“实践”

师选一组代表展讲，展讲小组展示并讲解三种方法如下：

展讲生：关于我们的方法大家有什么不明白的吗？

质疑生A：以前的除法竖式都是一条横线，这个除法竖式为什么是两条横线？

展讲生：因为计算了两次，先算60÷2=30，再算8÷2=4，所以是两条横线。

师引导：结合以前的除法竖式大家想想，一条横线表示什么？

片刻思考后有学生举起了手。

生：我觉得就是算了一次，也就是分了一次。

师：你真会思考，那么两条横线表示什么？

生（迫不及待）：我知道我知道，分了两次，第一次是分60个桃子，第二次是分8个桃子。

师：那么大家发现除法竖式有什么作用？

生：我觉得除法竖式一个很重要的作用是把平均分的过程表示出来了。

师：大家同意吗？（同意）我们把掌声送给她。

展讲生：谁还有疑问吗？

质疑生B： 以前竖式的商是一位数，今天为什么是两位数？

展讲生：刚才不是说了吗？分了两次，不就是两位数吗？

生B懵懵懂懂地坐下。

师再次介入。

师：第一次分60个桃子，每只猴子分到多少个呢？

生：每只猴子分到30个桃子。

师：也就是3个十，那么3应该写在哪一位上？

生：十位上。

质疑生B：老师我明白了，第二次分8只桃子，每只猴子4个桃子，也就是4个一，因此1写在个位上。所以是两位数。

师：触类旁通，你很会学习。

质疑生C：我还有一个问题，这道题这么简单，为什么要用这么麻烦的竖式？

生：是呢，我也这么觉得！

好多学生也纷纷点头。

师：是啊，没有这么麻烦的竖式，我们也过得挺好的，对于我们的数学学习好像也没什么影响，是不是我们真的就不用学了？

生：我觉得需要学，这道题是能用口算知道结果，但是如果以后遇到三位数或者四位数这样不容易口算出结果的，就需要用到竖式了。

生：竖式是为不容易直接算出的大数据计算做准备的。

……

师：是啊，有的知识着眼于眼前，能快速解决问题。有的知识着眼于以后，为我们的日后学习做准备。随着学习的深入，你们会不断感受到除法竖式的魅力！

……

从知识角度看，除法竖式是一种抽象的计算过程，它用最简洁的数学语言记录了“平均分”的过程，具有简洁性。由于学生需要按照“商、乘、减、比”等一系列程序步骤才能完成，计算过程本身的复杂性决定了它是整个计算教学的重点和难点，因此除法竖式的建构不是一蹴而就的，尤其是两层竖式，学生需要重新改造原有的认知结构，这在一节课中是无法实现的。作为教师，我们要充分了解学情，基于学生的认知需要，通过各种途径，为学生的知识建构提供一个更加坚实的平台，使其心甘情愿、自然而然地接受。