浅谈发展空间观念的几个策略

许丽荔

摘 要：空间观念是《义务教育数学课程标准（2011年版）》提出的十大核心概念之一。课堂教学中要让学生经历观察、操作、想象、抽象、综合分析、运用的过程，以帮助学生建立空间观念。

关键词：核心概念;空间观念;观察;操作;想象;联系;运用

中图分类号：G623.5 文献标识码：A 收稿日期：2019-02-18 文章编号：1674-120X（2019）10-0079-02

《義务教育数学课程标准（2011年版）》提出了十个核心概念，空间观念是十大核心概念之一，也是空间与图形学习内容的核心目标之一，它是形成数学核心素养的重要能力，是学生将来进一步深入学习平面几何、立体几何的基础，对培养学生的创新精神和实践能力有重要的作用。

一、在有目标的观察中发展空间观念

小学生的思维正处于直观形象思维向抽象逻辑思维的过渡阶段，他们对几何图形的认识多是从观察活动开始。教师可引导学生从不同的角度细致地观察图形的外形特征等，帮助学生逐步建立图形的表象，从而让其明确图形的特征，促进学生形成“空间观念”。教师要引导学生全面、有目的、有序地观察，还要与想象、推理、表达、思考有机融合。

在教学三角形的分类一课时，教师可出示一些不同形状的三角形让学生观察应该怎样分类，学生一时没有头绪，不知从何入手，教师可以引导学生思考：三角形有哪些特征？让学生领会可以从三角形的三条边的长短和三个角的大小方面来观察，思考给三角形分类的方法。学生虽然有了初步的思维方向，但对怎样分类还是没有方向，这时教师可再给学生出示这些三角形的每条边的长度以及每个角的度数，让学生进行细致的观察及交流，并动手分一分。有了这些具体的数据，三角形的三条边和三个角在学生的头脑中就鲜活起来，学生在观察边的长短中发现可以把三条边都不相等的三角形分为一类，两条边相等的三角形分为一类，三条边相等的三角形分为一类。在观察角的大小中发现，可以把有一个钝角的三角形分为一类，有一个锐角的三角形分为一类，三个都是锐角的三角形分为一类。学生在教师的引导下确立观察目标，从三角形的表象入手，在具体的数据中建立按角分的各类三角形和按边分的各类三角形的模型，从而顺利完成三角形的分类，发展空间观念。

二、在有意义的操作中发展空间观念

空间观念的形成，不能只靠观察，学生必须有自己独立动手操作的过程。教师要让学生的视觉、听觉、触觉等多种感官协同参与活动，使学生在画一画、比一比、折一折、叠一叠、剪一剪、拼一拼的过程中获得大量的感性知识，同时进行观察、尝试、想象、比较、综合、抽象分析，从而把握空间图形的本质，建立空间观念。

在教学三角形的面积时，教师可利用学生已有的知识经验，将学过的长方形、正方形、平行四边形的面积引入，出示面积分别为80cm2、100 cm2、120 cm2的长方形、正方形和平行四边形，并用一条对角线把每个图形分割成两个完全一样的三角形。学生通过观察发现：每个三角形的面积都是原图形面积的一半，分别是40cm2、50cm2、60cm2，初步感知三角形的面积与长方形、正方形、平行四边形的面积之间的关系，同时感悟用两个完全一样的三角形可以拼成以前学过的图形。但此时学生对三角形面积计算公式的理解并不深刻，教师需要进一步引导学生进行有意义的操作活动，给学生提供三角形学具让学生动手操作。为了让操作更有意义、更有效，教师在学生操作前要给学生温馨提示：①两个完全一样的三角形能够拼成已学过的什么图形？②请把拼成的图形画出来。③拼成的图形的各部分与原来的图形的各部分有什么关系？学生在尝试着拼一拼的过程中把两个完全一样的三角形转化成了长方形、正方形或平行四边形。这其中渗透了转化的数学思想。学生在画一画的过程中把直观的实物抽象成几何图形，在观察、比较、分析的过程中会发现三角形的各部分与拼成的图形之间的关系，并根据拼成的已知图形的面积计算公式推导出三角形的面积计算公式。这时教师可以再提出一个具有挑战性的问题：“还有其他方法能推导出三角形面积的计算公式吗？”学生的思维再次活跃起来，拿起学具，有的画，有的拼，有的剪……学生在动手操作过程中会发现用一个三角形也能剪拼成平行四边形或长方形，应用不同的思路、不同的方法同样能推导出三角形的面积计算公式。学生在经历观察、操作、比较、讨论、综合归纳等有意义的数学活动的基础上，可进一步体会转化思想的价值，发展空间观念。

三、在深刻的想象中发展空间观念

在学生经历一定的目的，有顺序、有重点观察建立图形的表象及在多种活动中获得大量的感性知识的基础上，我们要引导学生在脑海里想象，想象是建立在大量的实践的表象上的。我们要为学生插上想象的翅膀，让学生在深刻的想象中发展空间观念。学生对正方体的展开图的学习需要有一定的空间想象能力。在学生理解与掌握了什么是正方体的展开图之后，教师再给学生提供一些由六个小正形组成的图形，让学生来判断哪些图形折叠后能围成正方体。学生通过合作探究发现了两种研究方法：一种是动手折叠，一种是头脑想象。动手折叠比较容易，但是有一定的局限性，因此利用空间想象来解决问题就很有必要了。然后要求学生任选一个图形，利用空间想象来判断，并把每个面用“上”“下”“前”“后”“左”“右”标注出来。学生全员参与，展开想象的翅膀，在操作与想象中找到了先确定以相邻面比较多的一个面为下面，再确定前、后、左、右，最后再确定上面的巧妙方法。在对每个图形的折叠情况进行汇报的过程中概括总结出有6个在一排的，而6个在一排的展开不能折成正方体，中间一列（或一行）应该等于或小于四个才有可能拼成一个正方体。有田字、凹字也不能拼成正方体。在操作中想象，在想象中领悟，在领悟中概括，有了如此深刻的活动，学生既发展了空间观念，又提升了核心素养。

四、在沟通知识的联系中发展空间观念

小学数学知识的系统性很强，要让学生认识到知识是联系的、有结构的，这种结构具有整体性。几何知识也是一个互相联系的整体。教学中要让学生学会用自己的知识经验进行建构，把孤立、静止的知识联系起来。

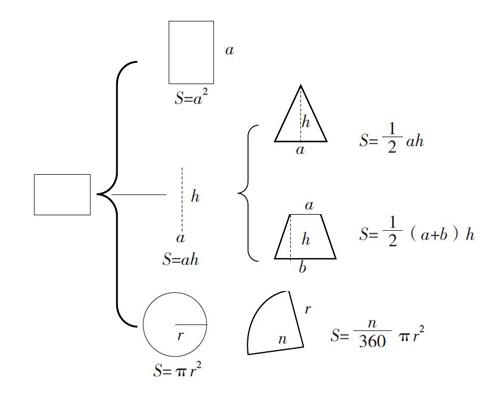
在进行面积的整理复习时，教师要让学生回顾各种图形面积计算公式的推导过程，并加以整理和归纳，把面积知识串成一片，形成条理化、系统化的知识网络。如以长方形的面积为主线、为旧知，把正方形、平行四边形和圆这些新知转化为旧知推导出正方形、平行四边形和圓的面积计算公式，再运用平行四边形的面积计算公式推导出三角形和梯形的面积计算公式，运用圆的面积计算公式推导出扇形的面积计算公式，突出长方形的面积这个核心知识的中心作用。这样既可认识到知识之间的共通性和差异性，又可提升空间观念。

五、在沟通理论知识与实际运用关系中发展空间观念

数学源于生活，离开了生活，数学就成了无源之水、无本之木。数学知识的生命在于应用。对空间与图形知识的学习不仅要求学生掌握形体的特征，领会形体的概念，理解形体的计算公式，更要求学生把这些知识运用于实际生活中，加深对知识概念的理解，丰富几何形体的空间形象，提高解决实际问题的能力，在沟通理论知识与实际运用关系中发展空间观念。教师要结合教学内容，引导学生用所学知识解决实际问题，让学生体会到生活中处处充满数学，数学就在身边。

学习了长方体和正方体的表面积和体积计算公式之后，教师可以设计替厂家设计新型饮料的包装箱的活动：每三盒装一箱，每盒长8厘米、宽6厘米、高12厘米。并引导学生进行讨论，初次设定方案：①每盒饮料必须正放;②要放得下3盒饮料，空隙不能太多，接缝处可以不计;③不管怎样设计，数量不变就是总体积不变。要求学生们算出自己所设计的包装箱的长、宽、高分别是多少，做出这样一个包装箱需要多少材料？学生分小组活动，有的画，有的记录，有的计算，找到了三种设计方法：第一种设计是把三盒饮料叠成三层，长8厘米，宽6厘米，高36厘米，表面积是1104平方厘米;第二种设计是把三盒饮料排成一排，把长12厘米、宽8厘米的面贴在一起，包装箱的长18厘米，宽8厘米，高12厘米，表面积是912平方厘米;第三种设计还是把三盒饮料排成一排，把长12厘米、宽6厘米的面贴在一起，包装箱的长24厘米，宽6厘米，高12厘米，表面积是1008平方厘米。第一种设计占地面积最小，但不够美观，并且容易把下面的饮料压坏，表面积也最大，所用的材料是最多的。第二种和第三种设计的占地面积一样大，外观也相差不大，但第三种设计的表面积比第二种大，所需要材料相对要多些，第二种设计所需要的材料是最少的。进一步追问：三盒饮料叠在一起，体积一样，为什么第二种设计的表面积是最小的呢？学生讨论交流发现：把最小的面拼在一起，拼成的长方体表面积最大，最大的面拼在一起，拼成的长方体的表面积最小。最后选择以第二种设计来确定设计方案。这个设计需要用到长方体、正方体的表面积和体积知识来解决，学生在探究并建构知识结构和能力结构的过程中可以体会数学知识之间、数学与生活之间的紧密联系。在设计过程中既有对学生数学知识与空间观念的检验，又有对学生人文精神的渗透。

总之，空间观念的形成是一个长期的过程。观察、操作、想象、运用等策略并不是孤立存在的，而是互相伴随、相互渗透，因而教师一定要按照学生的认识规律，让学生在操作中观察，在观察中想象，在想象中领悟，在领悟中概括，并注意在实际中运用，才能更好地培养和发展学生的空间观念。

参考文献：

[1]华 文.论如何培养小学生的空间观念[J].读写算（教师版），2015（29）：140.

[2]林凤蓉 .培养空间观念“六感”——空间与图形策略谈[J]. 小学教学参考（数学版），2011（26）：6-7.

[3]黄伟星.对“综合应用”领域的思考——“表面积的变化”教学实践与反思[J].复印报刊资料（小学各科教与学），2009（1）：17-21.