铁路圆端空心墩拟静力试验研究

李吉林，李明清，邵长江，王翔，漆启明



铁路圆端空心墩拟静力试验研究

李吉林1，李明清2，邵长江3，王翔4，漆启明3

(1. 中国铁路总公司 工程管理中心，北京 100844；2. 中铁二院工程集团有限责任公司，四川 成都 610031；3. 西南交通大学 土木工程学院，四川 成都 610031；4. 成兰铁路有限责任公司，四川 成都 610032)

针对圆端空心桥墩进行拟静力试验有助于了解该类桥墩的地震损伤机理，丰富铁路空心墩的抗震构造设计，进而完善铁路抗震设计理论和方法。以配箍率和轴压比为设计参数，进行5个1/6缩尺比的铁路空心墩拟静力试验，通过试验观测详细描述桥墩加载过程中的裂缝开展及损伤行为，分析桥墩的损伤机理，阐释加载过程中滞回特性的变化规律及影响因素，基于骨架曲线得到构件的最大水平抗力和位移延性系数，同时研究设计参数对构件抗震性能的影响规律，并对圆端空心墩的抗震设计提出意见和建议。

圆端空心墩；拟静力试验；滞回特性；骨架曲线；抗震性能

铁路桥墩一般采用截面刚度较大的圆端形截面[1]，对于高度大于30 m的铁路桥墩，为达到减小恒载、降低墩身基础经济投入并优化动力特性的目的，通常采用圆端空心截面[2]。然而，现行铁路桥梁抗震规范[3]尚未明确具体给出圆端空心截面铁路桥墩的抗震设计方法，而地震作用下空心墩相对于与实心墩在受力机理上的显著差异[4]，无法直接借鉴和引用实心墩的设计计算原理。为此，本文以实际工程项目为基础，针对工程中铁路圆端形空心墩抗震性能的开展相关理论分析和试验研究，可以为准确评估高烈度地震区的圆端形空心墩抗震性能以及铁路行车安全性提供理论依据和指导意义。目前，国内外针对空心墩的拟静力试验研究主要集中在矩形、方形和圆形空心截面[5−10]，基于这些试验，研究人员取得了大量成果，为丰富和完善矩形、方形以及圆形空心墩的抗震设计理论和方法提供了重要支撑。而关于铁路空心墩的试验研究主要成果相对较少，主要集中在国内几位研究人员的文献中。刘林[11]对配筋率较低的已有普通铁路空心墩进行了无轴压下的拟静力试验，并对铁路高墩的抗震设计提出了合理意见；夏修身[12]分别采用试验与数值模拟研究了铁路空心高墩的抗震性能，并提出合理配筋率及布置方式；蒋丽忠等[13]结合当前新建的高速铁路圆端截面空心墩，设计制作了10个大比例模型，研究了剪跨比、轴压比、纵筋率及配筋率对桥墩抗震性能的影响，但试验主要是横桥向加载。上述关于铁路空心墩的试验研究在一定程度上提升了我国铁路桥梁的抗震设计水平。然而仍然存在模型数量有限、缩尺比例较小，关于塑性铰区破坏机理、塑性铰的非线性行为等的分析有待深入，现有成果尚未集成为理论和方法体系。可见为了对于铁路圆端形空心墩的试验研究仍需加强。本文基于铁路中常采用的圆端空心30 m高墩为原型，以轴压比和配箍率作为变化参数，设计制作5个1/6缩尺的圆端形空心墩模型，进行拟静力试验，探究圆端空心墩受力过程中的裂缝分布规律，系统分析塑性铰区损伤行为及破坏机理，研究桥墩轴压比、配箍率对滞回特性、承载力及延性性能的影响规律。在此基础上，针对铁路圆端形空心墩的抗震设计提出一些建议，为今后的实际工程抗震设计提供一定的参考。

1 试验概况

1.1 模型设计

根据成兰铁路沿线工点设计图纸，选取简支梁桥墩高30~45 m范围内的代表性桥墩为原型。桥墩墩底固结，墩身为变截面。试验模型原型墩高为30 m，根据相似比理论取1:6进行缩尺模型设计。模型桥墩高为5 m，空心墩身为变截面，外壁坡度为40:1，内壁70:1，墩底倒角处壁厚11.3 cm，墩顶倒角处壁厚7.4 cm，所有模型的混凝土标号为C35，纵筋采用直径12 mm的HRB400带肋钢筋，箍筋为直径6 mm的HPB235光圆钢筋，具体桥墩尺寸构造及设计参数如图1和表1所示。模型设计时着重考虑配箍率和轴压比对于铁路圆端空心墩抗震性能的影响。另外，考虑到缩尺后墩身性能的对称性和配筋的可行性，缩尺模型的配筋率与原型桥墩略有差异。桥墩模型主要设计参数如表1所示，截面配筋设计如图1所示。

表1 桥墩模型参数特性

单位：cm

1.2 试验装置及测试方案

试验在西南交通大学陆地交通地质灾害防治技术国家工程实验室进行，竖向轴向压力采用液压千斤顶施加，水平荷载由MTS1000kN高性能全动态作动器提供，加载装置如图2所示。加载初始采用力控制，当墩身混凝土开裂后采用位移控制。各桥墩在测试过程中的直观表象和测试数据。直观表象包括裂缝的发展过程、保护层混凝土的剥落、箍筋的屈曲以及纵筋的屈曲、断裂等损伤情况。测试数据包括：墩顶总位移的弯曲变形、剪切变形和滑移变形分量和墩底截面的平均曲率、纵筋应变、截面曲率沿墩身高度的分布以及墩身侧向位移等。位移变形和曲率变形通过位移传感器测试，纵筋及箍筋应变通过钢筋应变计获取。

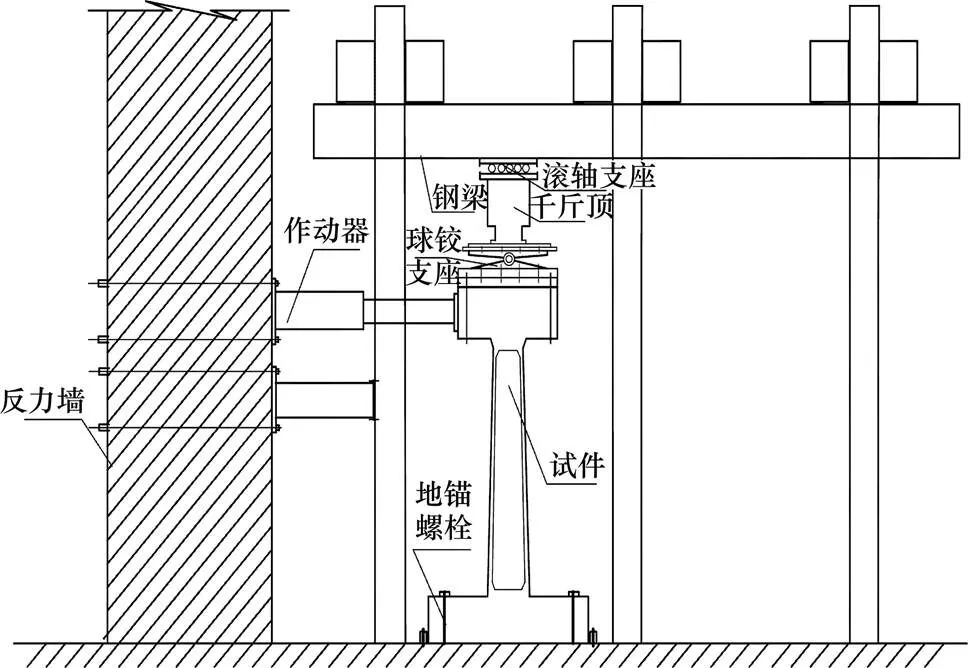
图2 加载系统示意图

2 试验结果

2.1 试验现象描述

5个桥墩均为弯曲破坏，并表现出了较好的延性性能。所有试件在加载过程中均经历了诸如弯曲裂缝的出现与发展、侧面斜裂缝的出现与发展、保护层混凝土的初始剥落与最终压溃等现象表现出的混凝土损伤全过程；而塑性铰区域纵向钢筋则出现了屈服、裸露变形等现象。

在试验加载过程中，由专门试验人员采用裂缝观察仪观察裂缝现象。1) 在构件即将开裂初期，构件根部、墩底实心段与空心段的交界处以及空心段截面突变处作为主要的观测区域；2) 在中低水平荷载作用下，潜在塑性铰区域作为重点观测区域；3)在高水平荷载作用下，潜在塑性铰区域的裂缝宽度、侧面斜裂缝、沿墩身高度产生的新裂缝以及纵筋屈曲作为重要的观测对象。

以S-A1为例，图3给出了桥墩底部塑性铰区域的最终损伤情况，图4给出墩身裂缝的分布情况，桥墩的详细损伤历程描述如下：

在第1次施加75 kN推力时，桥墩受压侧离墩底约5 cm处实心段出现竖向微小裂缝。可能原因：由于施工误差，造成此处混凝土保护层太薄，在自重、轴力和推力产生的多重压力下，此处保护层混凝土达到了极限压应变，由于泊松效应出现了受压竖向裂缝。施加第1次110 kN拉力时，在受拉侧离墩底约32 cm处混凝土因达到受拉极限应变出现微小的弯曲裂缝。位移加载时，第1次施加12 mm受拉位移时，受拉侧离墩底约40 cm处(空心端与实心墩交界处附近)出现横向贯通弯曲裂缝。

位移达到24 mm时弯曲裂缝快速延伸，从距离墩底40 cm处往上沿墩高方向几乎按等间距(约60 cm)往上出现数条新裂缝。墩身侧面斜裂缝开始发展且较为明显。原因在于此墩配箍率(0.325%)较低，抗剪能力较弱，在该水平荷载等级作用下，抗剪需求大于抗剪能力，故而斜裂缝出现时间早，且发展较快。第2次施加24 mm位移时，距离墩底45cm的空心段变截面倒角处的纵向钢筋首次屈服，并出现全截面贯通裂缝。

施加48 mm荷载水平时，原有裂缝宽度继续扩展的同时，正面出现8条新裂缝，侧面斜裂缝发展速度亦有所加快，斜裂缝较长较宽，斜裂缝已然穿过中性轴位置。荷载达到72 mm时，弯曲裂缝发展速度大幅度下降，仅有1~2条新裂缝出现，混凝土损伤情况主要体现在塑性铰区域的弯曲裂缝宽度的发展上。在施加第2次72 mm荷载时，受压侧距离墩底约50 cm处出现保护层混凝土初始剥落现象。水平位移达到96 mm时对应的最大承载力242.5 kN，方向施加96 mm时的最大承载力235.0 kN。在120 mm时，几乎没有新裂缝产生，塑性铰区域的裂缝宽度持续增大，承载力逐渐下降。140 mm时，受压侧混凝土压溃明显，纵筋裸露变形，承载力继续下降。位移达到168 mm时，受压侧混凝土进一步崩溃，裸露纵筋受压屈曲，承载力急剧下降至最大水平力的83%，达到极限状态，停止加载。

(a) 正面；(b) 背面

图4 S-A1墩身裂缝分布

2.2 滞回耗能特性分析

滞回耗能特性反映了桥墩耗散地震能量、抵抗地震力的能力，对于桥梁延性抗震设计尤为重要。桥墩的滞回耗能定义为力-位移滞回曲线中封闭滞回环包围的面积，滞回环面积越大桥墩的耗能能力越强(5个桥墩的滞回曲线如图5所示)。

5个试件的滞回曲线均较为饱满，表现出良好的耗能性能，各墩单周循环加载及累计的耗散能量，桥墩滞回耗能有如下特点：

1) 桥墩开裂以前，加载与卸载曲线近似直线，经过完整一次循环加载后滞回环所包围的面积很小，因此可认为其处于弹性状态，通过滞回耗散的能量极少；

2) 桥墩开裂后，试件的截面刚度与整体刚度逐渐下降，滞回环的面积开始逐渐扩大，当力卸载为0时的出现残余位移，并且该位移随着加载循环周次的增加而急剧增大；

3) 随着纵筋屈服、塑性铰的形成，滞回环愈发饱满，体现出良好的滞回耗能；

4) 在相同的位移水平下，由于损伤的累积，后一循环加载耗散的能量较前一循环加载耗散的能力小，特别是加载后期，这一特点愈为明显；

5) 随着控制位移的增加，虽然桥墩的承载力可能下降，但其耗散的能量仍可能增加；

6) 当纵筋发生屈曲时，桥墩的耗散的能量有明显的降低，特别是纵筋断裂时耗散的能量骤降。

上述试验表明，随着箍筋用量的增加滞回耗能稍有增加；随着轴压比的增大，桥墩滞回耗能有所增强，但轴压比过大时会使得墩底混凝土区域提前出现剥落压溃等现象(如试件S-B2)。当然配箍率及轴压比对试验现象的影响是否合理还需要更多圆端空心墩试验的验证以及相关理论的深入研究。

2.3 承载力及延性分析

将桥墩每一级荷载工况第1次循环所得的力-位移曲线达到最大峰值荷载点的轨迹作为此墩的骨架曲线，图6给出了各试件的骨架曲线。通过的骨架曲线，可以得到各桥墩试件的屈服位移/荷载、极限位移/荷载，从而获得桥墩实际的最大承载力以及延性。表2给出了各试件的承载力及位移试验值。其中，开裂位移cr是试验过程中墩身出现明显弯曲裂缝时对应的位移，由此可以避免因为施工质量及养护等原因造成的细微裂缝。屈服位移y由Park法[14]确定，同时可以确定相应的屈服强度。极限位移u是试件承载力下降至承载力最大强度85%时对应的位移。u/y为桥墩屈强比，u/y为延性系数。由图6及表2分析可知：

1) 通过比较配箍率不同的试件(S-A1，S-A2和S-A3)发现，虽然空心墩相对实心墩而言，截面严重削弱，箍筋约束效应减弱，然而随着配箍率的提高，试件的极限承载能力有了一定的提高，且表现出较好的延性。

2) 不同轴压比试件(S-A2、S-B1、S-B2)的抗震性能有较大差异。随着轴压比的增大，桥墩的承载力有了较大的提高，试件S-A2比S-B1的峰值荷载提高了近58%；但需要注意的是，轴压虽然一定程度上可以提高侧向承载力，但过大的轴压会使得桥墩提前出现压溃现象，导致期延性的降低(如S-B2)。

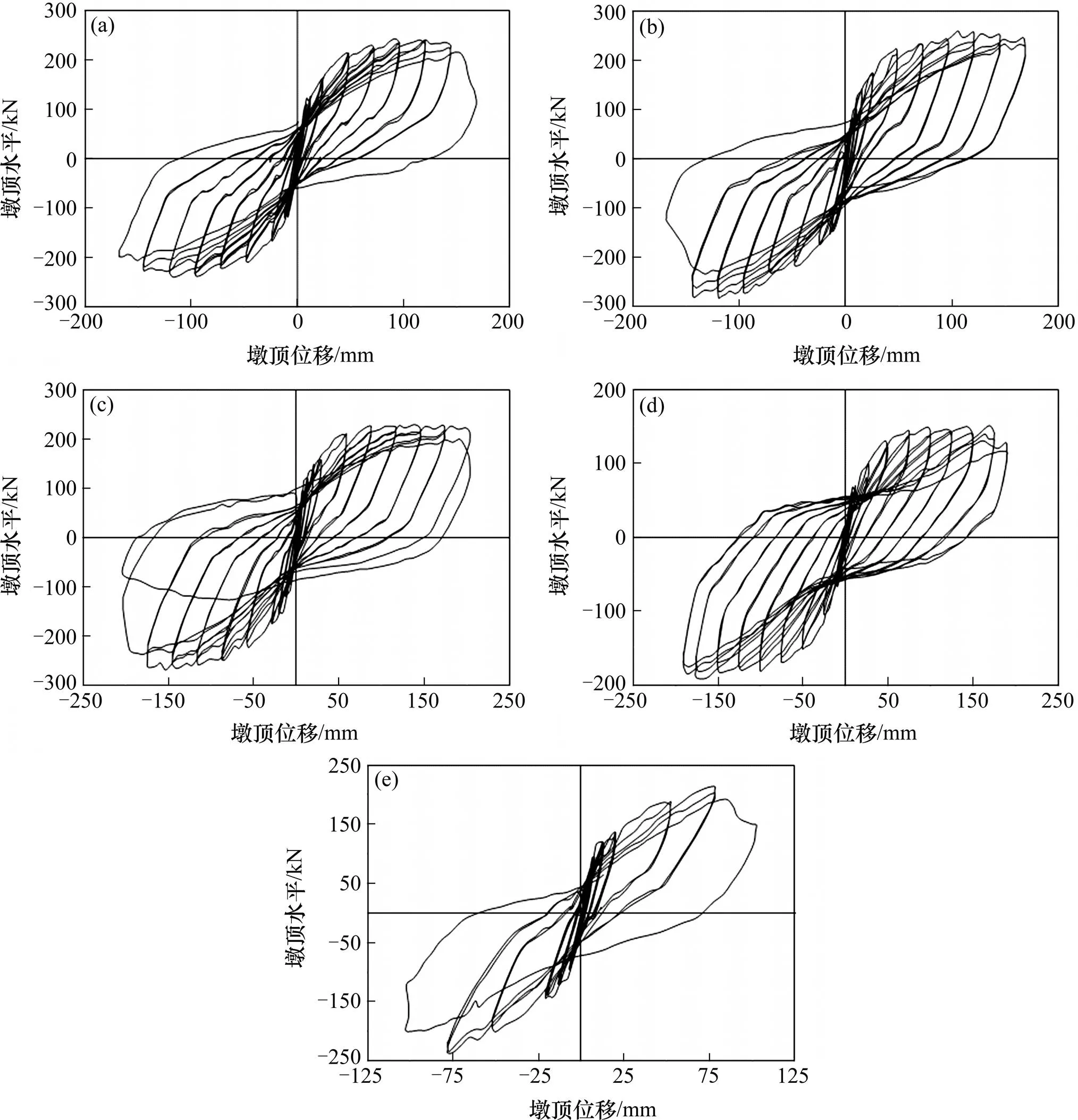
(a) S-A1滞回；(b) S-A2滞回；(c) S-A3滞回；(d) S-B1滞回；(e) S-B2滞回

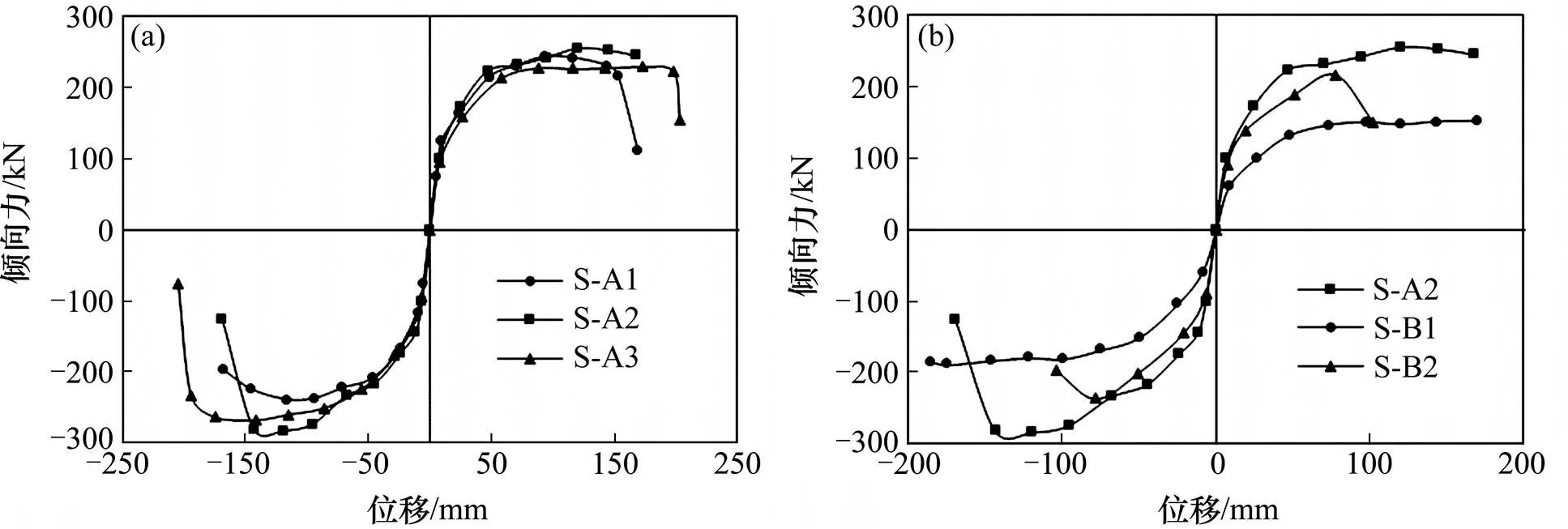
图6 各墩骨架曲线

表2 桥墩承载力及位移试验值

注：cr以桥墩出现明显弯曲裂缝时的位移为准，以略去由于施工养护等原因造成的细微裂缝

3 结论

1) 按照规范配筋的空心桥墩在地震下具有较大的塑性耗能能力，由于桥墩均为弯曲破坏，且S-A1，S-A2和S-A3的设计参数除了箍筋之外，其它均相同，实测滞回曲线非常接近。

2) 正交设计的S-A2，S-B1和S-B2设计参数除了轴压比不同外，其他参数均相同，三者之间的滞回曲线差异显著。

3) 配箍率对于桥墩侧向承载力影响较小，但可以提高其延性性能；轴压虽然一定程度上可以提高侧向承载力，但过大的轴压可能使得桥墩出现压溃现象，导致延性降低，在工程中应特别注意。

4) 箍筋用量对桥墩滞回耗能影响不显著，而轴压比的影响较大。

[1] 蒋丽忠, 邵光强, 姜静静, 等. 高速铁路圆端形实体桥墩抗震性能试验研究[J]. 土木工程学报, 2013, 46(3): 86−95.JIANG Lizhong, SHAO Guangqiang, JIANG Jingjing, et al. Experimental study on seismic performance of solid piers with round ended cross-section in high-speed railway[J]. China Civil Engineering Journal, 2013, 46(3): 86−95.

[2] 陈慧. 铁路桥梁圆端形空心墩的设计[J]. 铁道标准设计, 2009(4): 77−79.CHEN Hui. Design of round-ended hollow pier of railway bridge[J].Standard Design of Railway, 2009(4): 77−79.

[3] GB 50111—2006(2009), 铁路工程抗震设计规范[S]. GB 50111—2006(2009), Seismic design code for railway engineering[S].

[4] Vassilis K, Papanikolaou, Andreas J. et al. Numerical study of confinement effectiveness in solid and hollow reinforced concrete bridge piers: Analysis results and discussion[J]. Comput & Struct, 2009, 87(6): 1440−1450.

[5] Yeh Y K, MO Y L, YANG C Y. Seismic performance of rectangular hollow bridge columns[J]. J Struct Eng, 2002, 128(1): 60−68.

[6] Calvi G M, Pavese A, Rasulo A, et al. Experimental and numerical studies on the seismic response of RC hollow bridge piers[J]. Bull Earthq Eng, 2005, 3(3): 267−97.

[7] Shin M, Choi Y Y, SUN C H, et al. Shear strength model for reinforced concrete rectangular hollow columns[J]. Eng Struct, 2013(56): 958−969.

[8] 宗周红, 陈树辉, 夏樟华. 钢筋混凝土箱型高墩双向拟静力试验研究[J]. 防灾减灾工程学报, 2010, 30(4): 369−374.ZONG Zhouhong, CHEN Shuhui, XIA Zhanghua. Bi-axial quasi-static testing research of high hollow reinforced concrete piers[J].Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(4): 369−374.

[9] 孙治国, 王东升, 郭迅, 等. 地震作用下RC薄壁空心墩抗剪能力比较研究[J]. 土木工程学报, 2013, 46(12): 81−89.SUN Zhiguo, WANG Dongsheng, GUO Xun, et al Comparative study on shear strength of RC thin-walled hollow bridge piers under seismic effect[J]. China Civil Engineering Journal, 2013, 46(12): 81−89.

[10] 韩强, 周雨龙, 杜修力. 钢筋混凝土矩形空心桥墩抗震性能[J]. 工程力学, 2015, 32(3): 28−40.HAN Qiang, ZHOU Yulong, DU Xiuli. Seismic performance of reinforced concrete rectangular hollow bridge columns[J]. Engineering Mechanics, 2015, 32(3): 28−40.

[11] 刘林. 高墩大跨铁路桥梁抗震设计与减震控制研究[D].北京: 北京交通大学, 2004. LIU Lin. Seismic design and control of high pier long-span railway bridge[D]. Beijing: Beijing Jiaotong University, 2004.

[12] 夏修身. 铁路高墩抗震设计方法研究[D]. 兰州: 兰州交通大学, 2012. XIA Xiushen. Seismic design approach for high piers of railway bridge[D]. Lanzhou: Lanzhou Jiaotong University, 2012.

[13] 蒋丽忠, 邵光强, 王辉, 等. 高速铁路圆端形空心桥墩抗震性能试验研究[J]. 工程力学, 2014, 31(3): 72−82. JIANG Lizhong, SHAO Guangqiang, WANG Hui, et al. Experimental study on seismic performance of hollow piers with rounded rectangular cross section in high- speed railways[J]. Engineering Mechanics, 2014, 31(3): 72−82.

[14] Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1989, 22(3): 155−166.

(编辑 蒋学东)

Semi-static test of round-end hollow-section railway piers

LI Jilin1, LI Mingqing2, SHAO Changjiang3, WANG Xiang4, QI Qiming3

(1. China Railway General Co., Ltd, Engineering Management Center, Beijing 100844, China; 2. China Rail Eryuan Engineering Group Co., Ltd, Chengdu 610031, China; 3. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 4. Chengdu-Lanzhou Railway Co., Ltd, Chengdu 610031, China)

The semi-static experimental research will help us to understand the damage mechanism and update seismic detail design of round-ended hollow piers, which will also help to optimize the seismic design method of hollow piers in the current code of railway engineering. Therefore, five 1/6-scale specimens were tested by semi-static loading with lateral rebar ratio and axial compression ratio being the design parameters. The crack development and damage behaviors were investigated during the loading course. The damage mechanism of the piers was investigated in depth. The rules and effects of hysteretic curves were analyzed. The maximum lateral forces and displace ductility ratio were obtained based upon skeleton curves. The effects of the design parameters on the seismic performances of the specimens were studied at the same time. Several instructions were proposed for the seismic design of the round-ended hollow railway bridge piers.

round-end hollow-section columns; quasi-static tests; hysteretic property; skeleton curve; seismic performance

10.19713/j.cnki.43−1423/u.2019.05.017

U442.55

A

1672 − 7029(2019)05 − 1237 − 07

2018−07−08

邵长江(1970−)，男，山东临沂人，副教授，博士，从事桥梁抗震理论与试验研究；E−mail：shao_chj@swjtu.edu.cn