基于随机骨料投放的沥青混凝土细观模型研究
2019-06-06张富强滕旭秋李斌斌
张富强,滕旭秋,李斌斌
基于随机骨料投放的沥青混凝土细观模型研究
张富强,滕旭秋,李斌斌
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
为从细观角度研究沥青混合料,用ABAQUS内置脚本语言python建立一种考虑集料的棱角性、粗集料占比和混合料空隙率的随机骨料投放模型。在建模过程中,以椭圆为基准,引入旋转坐标,用椭圆短轴和随机区间控制骨料的形状。用卡罗蒙特法根据集料级配生成与实际情况较为相符的不规则多边形骨料的沥青混合料二维数字模型。在骨料重叠判定上,直接以多边形骨料本身为目标进行判断而舍弃以椭圆为目标的判断方法。用体视学方法得到沥青混合料的二维级配,制作二维数字试件。通过模拟单轴压缩和单轴拉伸试验,与真实形状的骨料模型进行对比,表明本文生成的二维随机沥青混凝土模型与真实骨料模型较为接近。
细观;python;随机骨料投放;体视学;多边形骨料
沥青混合料是一种集石料、矿粉和胶结料于一体的复合材料。为了检测沥青混合料的性能,一般需要成型马歇尔试件、小梁试件和车辙板试件。目前基于试验来研究沥青混合料性能的方法已相当成熟,一方面,这些试验只能从宏观角度反映试件的整体性能,而不能从细观角度深入分析混合料内部的受力特点及变形情况;另一方面,有时候试验量大短期内难以完成或因设备昂贵难以实现。为此,本文建立了能够反映沥青混凝土细观特征的随机骨料投放模型。在混凝土随机骨料数值模拟方面,部分学者已取得了一些进展,Milad等[1]提出了一种图像扫描与集料混合的随机生成沥青混凝土二维数字试样的方法。CHEN等[2]采用蒙特卡洛随机骨料模型,通过单轴拉伸模拟,研究了试件尺寸、粗集料面积占比和孔隙率对混凝土名义抗拉强度的影响。CAO等[3]利用随机骨料有限元模型预测沥青混凝土材料的动态模量。WANG等[4]提出了一种二维非均质细观混凝土试件的生成过程,在柔性实体网格中预先插入具有软化牵引分离关系的零厚度黏结界面单元,以模拟复杂裂纹的萌生和扩展。MA等[5]实现了用细观有限元模拟研究全级配混凝土的弯曲破坏过程。李坛等[6]将椭球体方程进行改造,在方程中引入随机变量及控制参数,生成了不规则多面体骨料。梁建等[7]用AUTOCAD内置语言VBA分别生成二维和三维多面体骨料,并运用交点法判断骨料是否相交,但此种方法要想将生成的模型导入有限元软件,还需处理转换成SAT格式,通用性不强。屈瑾等[8]用MATLAB软件生成了圆形、多边形及椭圆形随机骨料,但要想在有限元中计算,需借助MATLAB与AUTOCAD接口转换成SAT格式,过程相当繁琐。程一磊等[9]用生成的随机骨料模型进行三点弯曲试验模拟并验证了与试验结果的一致性。谢军等[10]用数字图像处理技术获取沥青混合料的截面图,通过二值化等图像处理技术得到沥青混合料粗集料轮廓进行数值分析。但这种方法必须以试验为基础才能进行。目前,现有的随机骨料模型大多是借助第三方编程软件实现随机骨料模型的建立,或直接通过图像处理,然后再导入有限元软件实现计算,在骨料重叠判定方面和骨料随机旋转分布等方面还不足。本文在椭圆方程的基础上引入旋转坐标和随机角度分布,以椭圆长轴为骨料直径,利用椭圆短轴控制集料高度,更加真实地再现了骨料的棱角、形状以及随机分布等特征。
1 二维随机骨料模型级配
1.1 二维级配的转化
陈俊等[11]提出运用体视学方法将三维体积级配转换为二维数量级配的方法,见式(1)~(5)。

为二维截面上所有截面圆的直径;为三维集料直径的所有组数;表示级配矩阵。
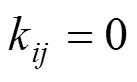
(3)
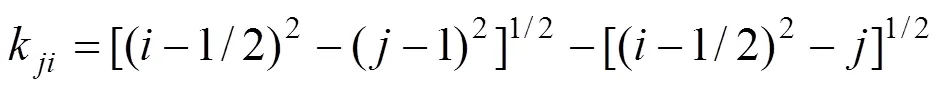


1.2 集料个数的确定
沥青混合料试件是由沥青、粗集料和细集料等组成的,由于生成粒径较小的颗粒时数量非常庞大难以实现,本文以2.36 mm为界,将沥青以及2.36 mm以下的细集料作为沥青砂浆形成一个整体,将2.36 mm以上的集料以随机投放的方式生成。为了得到2.36 mm以上各档集料颗粒数量,需要知道这部分集料的所占比例。陈俊等[11]通过成型不同级配的沥青混合料试板,将得到切片图像进行二值化处理得到了集料的面积和沥青砂浆的面积,表1为不同级配的沥青混合料对应的粗集料占试件的面积比值。

表 1 不同沥青混合料的粗集料占比
为了方便计算出各档二维集料的数量,需计算出各档集料的等效粒径面积,表2为各筛孔的等效粒径面积。

表2 各筛孔的等效粒径面积
为简化计算,以等效圆面积作为不规则多边形骨料的面积,由式(1)及式(6)可计算得到各档集料粒径范围内的数量,为后面生成随机骨料模型做 准备。
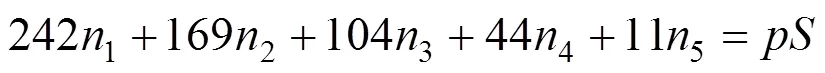
式中:1~5为各档集料的数量;为不同级配类型的粗集料占比;为二维沥青混合料数字试件的 面积。
2 二维随机骨料模型的生成
2.1 不规则多边形骨料的生成
为使沥青混合料中集料的形状更接近实际状况,本文采用极坐标的方式生成了随机不规则多边形,如图 1所示,按式(7)~(9)来以实现。首先以骨料粒径大小为长轴,为短轴的椭圆为基础,然后将该椭圆平均分成等份,在每个区间内随机生成一点作为该多边形的一个顶点。在0°~36°范围内随机生成个这样的顶点,然后依次连接即可生成所需多边形骨料。


(=1, 2, 3,…,) (9)
式中:为多边形的边数;,为多边形骨料极坐标原点;,为多边形顶点的角度取值范围;为在区间(,)上随机取一个角度;x,y为多边形顶点坐标值。

图1 不规则骨料生成示意图
2.2 多边形骨料干涉判断
在建立沥青混凝土二维细观结构时必须考虑集料之间是否重叠的问题,从而接近沥青混合料的骨架嵌挤结构。王江洋等[12−13]用2集料各边相交的点是否在集料边上判断集料是否相交,本文利用python内置函数min( )与max( )得到当前投放集料的各控制点坐标x~x,y~y的最小值与最大值,然后与已投放各集料的X~X,Y~Y进行比较判断。如果满足式(10)~(12)中的1个条件并且满足式(13)~ (14)中的1个条件则重叠,否则生成当前骨料,直到生成所有的所需骨料。各骨料重叠情况如图 2~6 所示,其中(a)表示已投放骨料,(b)表示当前投放 集料。

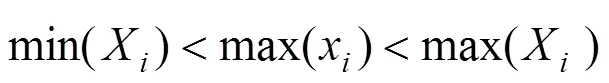
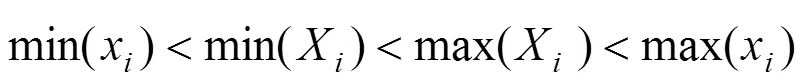
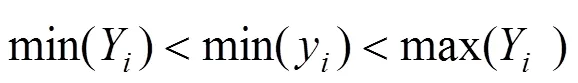
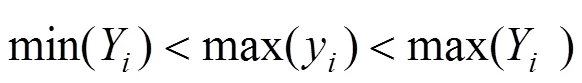

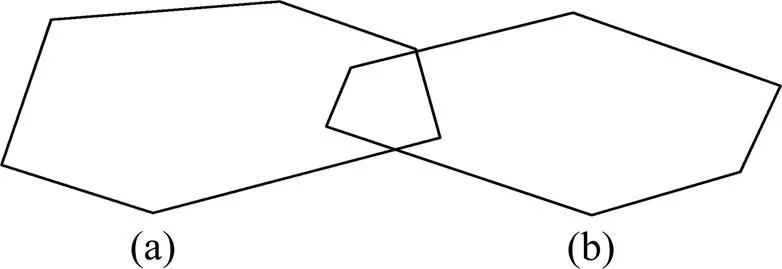
图2 当前投放集料的xmin在已投放骨料内
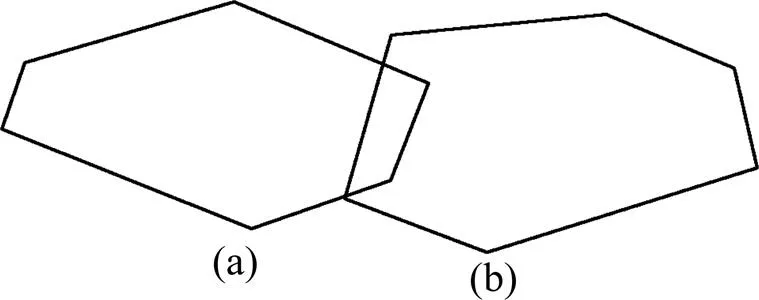
图3 当前投放集料的xmax在已投放骨料内

图4 已投放集料的xmin和xmax在当前投放骨料内
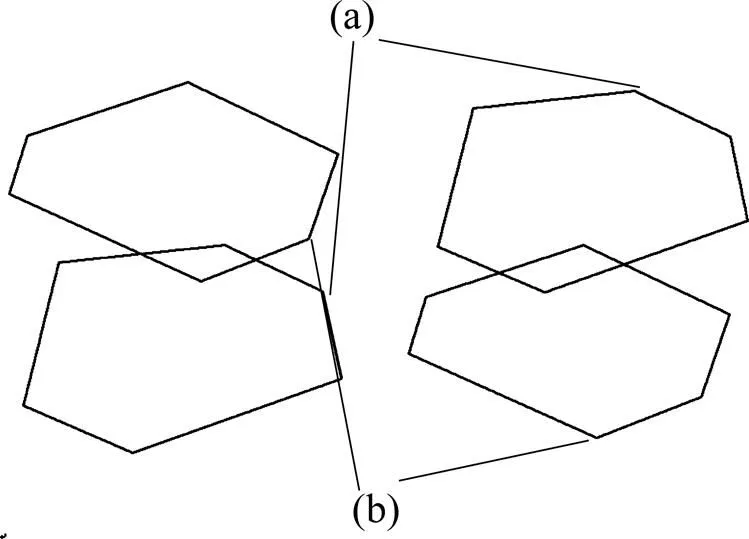
图5 当前投放集料的ymin或ymax在已投放骨料内
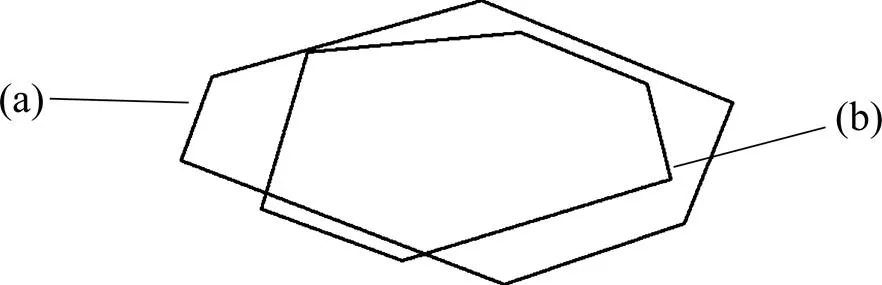
图6 已投放集料的ymin和ymax在当前投放骨料内
2.3 多级配随机投放

1) 给定矩形区域的宽度最小值min,宽度最大值max,长度最小值min,长度最大值max。
2) 按照各档集料个数比例计算各组粒径的投放数量。
3) 按照各组粒径的投放数量用随机函数random. uniform(r~r+1)生成各档集料的半径。
4) 在矩形区域内随机生成一点(,)作为椭圆极坐标的原点,并生成所需控制点。
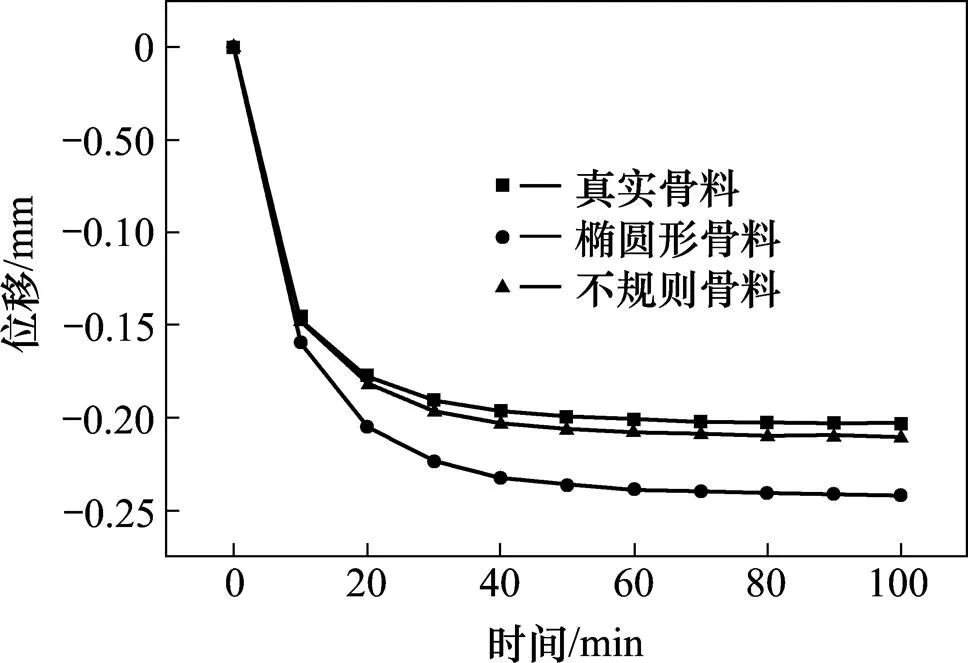
5)如果(−>min) and (+ 6) 判断当前生成骨料与已生成骨料是否重叠,如果重叠则跳出循环,否则生成当前骨料。 7) 根据已有的不规则多边形各控制点坐标,运用python语言在abaqus中实现不规则多边形随机骨料模型的建立。 图7 多边形骨料生成流程图 以AC-13为例,采用数字图像技术得到图8所示的真实骨料模型,用随机骨料投放方法生成图9所示的不规则多边形骨料模型,对这2种模型分别进行单轴压缩、单轴拉伸数值计算,根据沥青混合料时间与位移的关系来验证本文生成的不规则骨料。模型尺寸为60×60。在模型顶部加1个5 mm厚的钢板以保证各点位移变化均匀,钢板和模型为完全黏结。根据文献[14]的研究,本文将单轴压缩与拉伸荷载均取为0.12 MPa。骨料为玄武岩,弹性模量40 GPa,泊松比为0.2,矿粉为石灰岩,沥青为基质沥青。钢板弹性模量取为210 GPa,泊松比为0.3,沥青砂浆选用Burgers蠕变模型,其本构方程为 式(17)中:1和2为弹性模量;1和2为黏性系数,可将其转换为prony级数。 由文献[14]得到20 ℃时沥青砂浆的Burgers模型参数的prony级数见表3。 表3 沥青砂浆的prony级数 图8 真实骨料模型图 图 9 不规则多边形骨料模型图 图 10 椭圆形骨料模型图 数值计算结果表明,本文生成的不规则随机多边形骨料和真实骨料模型具有良好的一致性。由图11的单轴压缩试验结果可知,真实骨料和不规则骨料模型的最大压缩位移差值仅为7.995×10−6 m,其中不规则骨料的最大压缩位移为2.11×10−4 m,真实骨料的最大压缩位移为2.03×10−4 m。椭圆形骨料的最大压缩位移为2.41×10−4 m。不规则骨料与真实骨料的误差为3.8%,而椭圆形骨料与真实骨料的误差为14.21%。由图12的单轴拉伸试验结果可知,真实骨料和不规则骨料模型的最大拉伸位移差值仅为5.821×10−6 m,不规则骨料的最大拉伸位移为4.20×10−4 m,椭圆形骨料的最大拉伸位移为4.83×10−4 m。真实骨料的最大拉伸位移为4.08×10−4 m。不规则骨料与真实骨料的误差仅为1.4%,而椭圆形骨料与真实骨料的误差为18.4%。这说明骨料的形状与分布对试验结果影响很大。本文生成的不规则骨料模型在一定程度上和真实骨料模型具有相同的分布规律。 图11 单轴压缩数值模拟 图12 单轴拉伸数值模拟 1) 建立二维沥青混凝土细观数值模型,能够通过混合料级配随机生成二维沥青混合料数字试件,为沥青混合料数值模拟提供简洁有效的途径。 2) 以椭圆坐标方程为基准,以椭圆的长短轴为指标控制集料的长宽比,并引入旋转坐标,使生成的集料在二维平面可以以任意姿态分布。在集料交叉判定上直接以生成的不规则多边形为判定基准,摒弃了传统的以椭圆为基准的方法,使随机投放更加接近真实状况。 3) 将生成好的二维数字试件应用于模拟单轴压缩与单轴拉伸试验,与真实骨料模型进行对比分析,生成的不规则骨料模型在一定程度上和真实骨料模型相接近。其中单轴压缩试验的不规则骨料与真实骨料的误差为3.8%,单轴拉伸试验的不规则骨料与真实骨料的误差为1.4%。 [1] Milad S, HAO W. Image-aided random aggregate packing for computational modeling of asphalt concrete microstructure[J]. Construction and Building Materials, 2018, 177: 467−476. [2] CHEN Changhong, ZHANG Qian, Kerr L M, et al. The multi-factor effect of tensile strength of concrete in numerical simulation based on the Monte Carlo random aggregate distribution[J]. Construction and Building Materials, 2018, 165: 585−595. [3] CAO P, JIW F, CHANG J Z, et al. Investigation on statistical characteristics of asphalt concrete dynamic moduli with random aggregate distribution model[J]. Construction and Building Materials, 2017, 148: 723−733. [4] WANG X F, YANG Z J, Yates J R, et al. Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores[J]. Construction and Building Materials, 2015, 75: 35−45. [5] MA Huaifa, XU Wenxiang, LI Yuncheng. Random aggregate model for mesoscopic structures and mechanical analysis of fully-graded concrete[J]. Computers & Structures, 2016, 177: 103−113. [6] 李坛, 朱慈勉. 混凝土随机多面体骨料模型的生成方法[J]. 结构工程师, 2011, 27(4): 23−27. LI Tan, ZHU Cimian. Method for generating random polyhedron aggregate model of concrete[J]. Structural Engineer, 2011, 27(4): 23−27. [7] 梁建, 娄宗科, 韩建宏. 基于AUTOCAD的混凝土骨料建模分析[J]. 水利学报, 2011, 42(11): 1379−1383. LIANG Jian, LOU Zongke, HAN Jianhong. Modeling and analysis of concrete aggregate based on AUTOCAD [J]. Journal of Hydraulic Engineering, 2011, 42(11): 1379−1383. [8] 屈瑾, 娄宗科, 刘兆松. 基于细观层次的混凝土随机骨料建模[J]. 长江科学院院报, 2015, 32(4): 129−132, 138. QU Jin, LOU Zongke, LIU Zhaosong. Random aggregate modeling of concrete based on meso level[J]. Journal of Yangtze River Academy of Sciences, 2015, 32(4): 129− 132, 138. [9] 程一磊, 杨新华, 张川川. 沥青混合料三点弯曲断裂的扩展有限元模拟[J]. 固体力学学报, 2017, 38(3): 281− 286. CHENG Yilei, YANG Xinhua, ZHANG Chuanchuan. Expansion finite element simulation of three point bending fracture of asphalt mixture[J]. Journal of Solid Mechanics, 2017, 38(3): 281−286. [10] 谢军, 袁畅. 蠕变剪切试验前后粗集料运动轨迹的数字图像分析[J]. 土木工程学报, 2016, 49(9): 123−128. XIE Jun, YUAN Chang. Digital image analysis of coarse aggregate movement track before and after creep shear test[J]. Civil Engineering Journal, 2016, 49(9): 123−128. [11] 陈俊, 张东, 黄晓明. 离散元颗粒流软件(PFC)在道路工程中的应用[M]. 北京: 人民交通出版社, 2015.CHEN Jun, ZHANG Dong, HUANG Xiaoming. Application of discrete element particle flow software (PFC) in road engineering[M]. Beijing: People’s Transport Press, 2015. [12] 王江洋, 钱振东. 沥青混合料非均质多层次结构数字试件的二维随机生成算法[J]. 公路, 2016, 61(2): 17−21. WANG Jiangyang, QIAN Zhendong. Two dimensional random generation algorithm for asphalt mixture heterogeneous multi-layered digital specimen[J]. Highway 2016, 61(2): 17−21. [13] 任志刚, 徐彬, 李培鹏, 等. 二维混凝土骨料随机生成与投放算法及程序[J]. 土木工程与管理学报, 2015, 32(1): 1−6. REN Zhigang, XU Bin, LI Peipeng, et al. Algorithm and program for stochastic generation and delivery of two-dimensional concrete aggregate and program[J]. Journal of Civil Engineering and Management, 2015, 32(1): 1−6. [14] 李阳. 含非规则骨料的混凝土细观建模与分析[D]. 合肥: 合肥工业大学, 2017.LI Yang. Meso modeling and analysis of concrete containing irregular aggregates[D]. Hefei: Hefei University of Technology, 2017. (编辑 涂鹏) Meso mesoscopic model of asphalt concrete based on random aggregate placement ZHANG Fuqiang, TENG Xuqiu, LI Binbin (College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China) In order to study asphalt mixture from a micro perspective, a random aggregate delivery model was built by using ABAQUS built-in script language python. The model considered the Aggregate Angularity, coarse aggregate proportion and mixture porosity. In the process of building the model, the rotating coordinates were introduced with ellipse as the reference, and the shape of the aggregate was controlled by the elliptical short axis and the random interval. Two dimensional digital model of asphalt mixture material card remount method according to the aggregate gradation and the actual situation was consistent with the formation of irregular polygon aggregate. It was more close to the actual situation that the objective of the polygon aggregate itself was judged on the aggregate overlap and the ellipse as the target. The two-dimensional gradation of asphalt mixture was obtained by stereological method, and a two-dimensional digital specimen was made. Through the simulated uniaxial compression and uniaxial tensile test, the comparison with the real shape aggregate model shows that the two dimensional random asphalt concrete model is close to the real aggregate model. microview; python; random aggregate delivery; stereology; polygon aggregate 10.19713/j.cnki.43−1423/u.2019.05.014 U416 A 1672 − 7029(2019)05 −1216 − 07 2018−07−16 滕旭秋(1975−),女,黑龙江双鸭山人,副教授,博士,从事道路与铁道工程研究;E−mail:85461272@qq.com
3 模型验证与分析
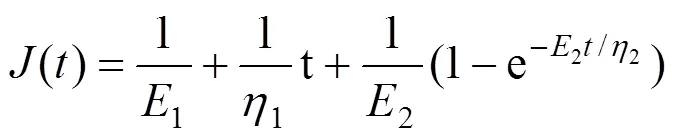





4 结论
