混合目标场景多点协同定位可定位性探讨

郭名静 ，边少锋 ，熊 鑫 ，单潮龙 ，张 伟

（1. 海军工程大学 电气工程学院，武汉 430033；2. 东华理工大学 理学院，南昌 330013；3. 海军工程大学 研究生院，武汉 430033）

0 引言

卫星定位是利用已知卫星的精确位置坐标和距离确定目标位置的方法，其基本原理是空间后方交会，即以卫星和用户接收机天线之间的距离的观测值为基础，根据已知的卫星瞬时坐标来确定用户接收机所对应的点位[1]。卫星定位技术在大地测量、高速铁路、精细农业、防灾监测、车辆导航、物流运输、位置服务等领域有广泛的应用需求的问题，但是在人口聚集、环境特殊的恶劣场景中都会存在由于缺少足够多的可见卫星而无法满足定位需求。协同思想为特殊环境中的卫星定位提供了一条新的解决思路。协同学（synergetics）的概念最早由联邦德国斯图加特大学教授、著名理论物理学家赫尔曼·哈肯（Hermann Haken）于1969年提出[2]，为生物学，乃至以后的计算智能、通信等领域研究提供了新的思路。

协同定位（cooperative positioning）是指在特定时刻的某一个定位场景中，如果未知的待测节点之间能够具备通信功能实现节点自身信息、定位场景环境信息等的交互，或者是待测节点之间可以通过通信等方式进行测距，也就是说具备节点之间的测量功能，或者是待测节点能够利用以前的定位信息，就可以协助完成当前时刻的定位需求任务。协同定位的发展历史开始于20世纪90年代，文献[3]在多机器人定位的研究中引入协同学的方法，并第一次提出了“协同定位”的概念。2000年，文献[4]通过给机器人安装摄像头和激光测距仪等设备来发现其他机器人，提出了基于采样的多机器人马尔科夫定位算法，可以计算得到移动机器人在任何时间的位置。

在“卫星协同定位”研究领域，最早是在2004年瑞典国防研究院在美国导航学会国家技术会议(national technical meeting of institute of navigation，ION-NTM)上首次提出在卫星定位中引入协同的概念[5]；文献[6]也在本次会议上提出了将协同理念应用到卫星定位；2012年，文献[7-8]从卫星定位视角出发，研究了协同定位对终端平均捕获时间的影响，及一些特定场景下定位性能和定位算法。

综上所述可以看到，协同定位被越来越多地应用在各种定位场景，作为一个贯穿多种定位研究需求的横断研究领域，其实用性不断得到认可，并正逐渐成为一个充满前景的研究领域。尽管相关研究已经取得了部分进展，但还有许多地方值得进一步研究，例如：协同定位数据处理算法，影响定位精度的因素分析，对多种场景下的协同定位体制的抽象建模，以及对协同定位场景下的可定位性、定位理论研究等[9-13]。本文假设不同收星条件的具体场景，分别构建卫星多点协同定位模型，对可定位性和定位算法进行研究。

1 协同定位的可收星节点数判定

一般情况下，只要地面节点能够接收到4颗及4颗以上卫星的信号，则待测定位节点就能够实现单点定位[14-15]。卫星单点定位算法要求得的是终端节点的 3维坐标（x,y,z）和钟差t，至少需要有 4个方程组成方程组，所以当该终端用户节点能够接收到至少4颗卫星信号时，才能够获得该节点的位置坐标信息。但是，在一些恶劣定位场景下，如室内、城市峡谷隧道以及森林等被遮蔽的复杂环境中，则会由于缺少足够多的可见卫星而无法实现单点定位，由此引入协同定位的理念。

“协同定位”的核心思想就是通过允许待测的未知节点之间以数据交换方式共享各自的先验条件信息，弥补单个待测未知节点先验已知条件信息不足造成的无法实现卫星定位的问题，从而实现参与协同的多个待测未知节点均可以获取位置信息实现定位。通过协同共享，原本缺少卫星信号不能实现单点定位的节点就有可能实现定位。

构建定位场景，假设待测节点接收到的卫星数目不足4颗，要实现每个待测未知节点的定位则需要判定单个待测未知节点接收到的卫星信号数目与参与协同的待测未知节点数目的关系。根据全球定位系统（global position system，GPS）的伪距方程和距离方程，在节点之间的距离信息可以测得，时钟信息先验已知的前提下，假设单个待测未知节点接收到的GPS卫星数目为M，能够实现定位的最少节点数为N。可以发现，方程组的未知数的个数为4N，需要的方程组中的方程个数也为4N，而方程组由所构建的个伪距方程个节点间距方程及个接收机钟差关系方程共同组成，即有

简化得到收到的卫星数目M与最少节点数N之间的关系式为

1）单个待测未知节点接收到的 GPS卫星数目M=4颗。根据卫星的伪距方程为

式中：待测未知节点A的坐标为（xA，yA，zA）；接收到的 4 颗 GPS 卫星的坐标为（xi，yi，zi）（其中i=1，2，3，4）；b为节点A与各卫星之间的钟差；ρi为第i颗卫星到节点A之间的伪距。因节点A收星数目为4颗，可得到以下伪距方程组求解得到4个未知数（xA，yA，zA，b）为则当收到的卫星数目M=4时，最少节点数N=1。

2）单个待测未知节点接收到的 GPS卫星数目M=3颗。节点A和B的坐标分别为（xA，yA，zA）和（xB，yB，zB），b1和b2为节点A和B与各卫星之间的钟差，且b1-b2为一个常数a。ρi(其中i=1，2，3)为第i颗卫星到节点A之间的伪距，为第i颗卫星到节点B之间的伪距。根据卫星的伪距方程可以得

若方程组有解，则2个待测定位节点A和B可协同定位；如果方程组没有解，则节点A和B不可以协同定位。

则当收到的卫星数目M=3时，最少节点数N=2。

3）单个待测未知节点接收到的 GPS卫星数目M=2颗。节点A、B和C的坐标分别为b1、b2和b3为节点A、B和C与各卫星之间的钟差，且差值均为常数ai(其中( 其 中i=1，2)为第i颗卫星到节点A之间的伪距，ρi′(其中i=34 )，为第i颗卫星到节点B之间的伪距，(其 中i=5，6)为第i颗卫星到节点C之间的伪距。可以列方程组为

则当收到的卫星数目M=2时，最少节点数N=3。

2 混合定位目标场景中的可定位性判定

基于北斗卫星导航系统（BeiDou navigation satellite system， BDS）的伪距单点定位原理，即通过让待测节点（接收机）接收4颗及以上的卫星信号，利用卫星导航电文与星历数据解算出卫星的坐标位置，再利用卫星与用户的空间几何关系构造出4个方程求解得到待测节点（接收机）的位置坐标，即

式中：c为光速；tA为待测节点（接收机）的时钟差；toi为第i颗卫星的时钟差，则（7）可以简化为

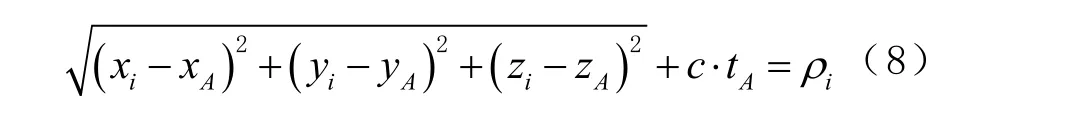
若待测节点都可以接收到相同数目的卫星信号，则根据式（2）可以判定BDS的收星数目M与最少节点数N之间的关系。

若待测节点并非都可以接收到卫星信号，比如有节点由于某些原因，如在室内或遮挡等，无法收到任何卫星信号，但所有待测节点之间均能通过通信或激光测距获取相互间的距离信息，且可以接收到的卫星时钟差信息都先验已知，则需要判定多点协同可定位性。

假设可收星节点数为N，不可收星节点数为N′，若每个不可收星节点的位置坐标为3维坐标可以发现，要求解不可收星节点数，则距离方程未知数的个数为 3N′与需要的方程个数之间可以建立关系式为

简化得到可收星节点数N与不可收星节点数N′之间的关系式为

因此，根据式（2）和式（10）判定混合协同定位场景下的可定位性如下：

1）当收到的卫星数目M=4、可收星节点数N=1、不可收星节点数为N′=5时，可定位。

则根据前文可知，可收星节点的位置坐标可得。同时，当不可收星节点数N′≥3时，在相同高程条件（即待定位节点具有相同高程值，按照2维坐标求解）下利用距离方程可以得到不可收星节点位置坐标，即也可定位。

2）当收到的卫星数目M=3、可收星节点数N=2、不可收星节点数为N′=3时，可定位。

则根据前文可知，可收星节点的位置坐标可得。同时，当不可收星节点数为N′≥1时，在相同高程条件下利用距离方程可以得到不可收星节点位置2维坐标，即也可定位。

3）当收到的卫星数目M=2、可收星节点数N=3、不可收星节点数N′=1时，可定位。

3 混合定位场景下多点协同定位算法

根据前文可知，如果节点收星数量少于4颗时，单点定位无法实现，需要判断是否能够实现协同定位。假设某混合目标定位场景，有′个节点终端，其中有N个节点可以接收到M个卫星信号，N′个节点不可以接收到卫星信号。

1）当收到的卫星数目M=3，可收星节点数N=2，设不可收星节点数为N′=3（如图1所示）。

图1 接收3颗卫星的多点协同定位

假设分别有A、B节点各自都只能接收到3颗BDS的卫星信号，有节点P、Q、S由于某些原因无法收到任何卫星信号。设（其中i=a，b，p，q，s）(其中j=1，…，n)表示节点可收到的卫星的坐标。ρji表示第j颗可收到的卫星到节点i之间的伪距，且先验已知。A、B节点的时钟差分别为ta、tb和tc且未知，卫星的瞬时钟差为tj，且先验已知。同时A和B之间的距离为dab，A和P、Q、S节点之间的距离dap、daq、das，B和P、Q、S节点之间的距离为dbp、dbq、dbs，P、Q、S节点之间的距离dpq、dps、dqs都分别可以测量得到，c为光速。分别标识节点A、B、P、Q、S节点的 3维坐标，

根据式（7）可以分别得到节点A、B的伪距方程为

将对于节点A方程式（11）移项变换可得到

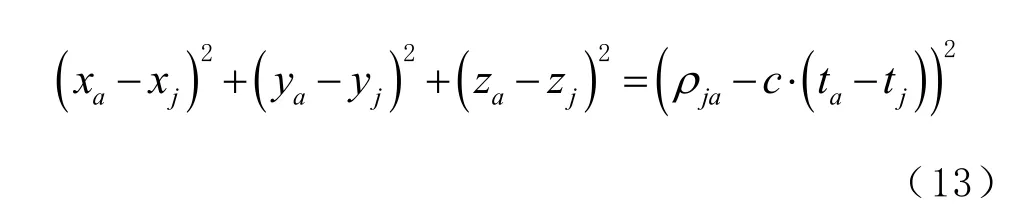
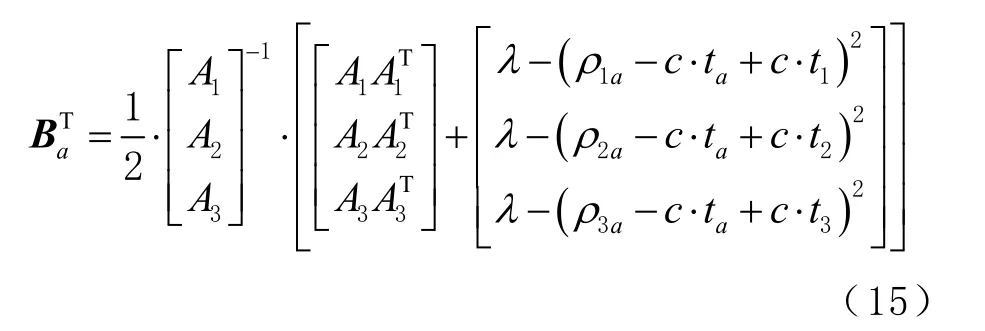
在式（15）中，节点A的坐标值是否可得，需要判断所接收到的3颗卫星坐标位置矩阵的逆矩阵是否存在。如果不存在，可判定该节点所收到的3颗卫星组成的星座结构不理想，节点A和B不能实现协同定位。若3颗北斗卫星坐标位置矩阵可逆，则由可以得到节点坐标值与节点A终端接收机时钟差的关系式同样的，也可以得到节点B终端的位置坐标与终端接收机时钟差的关系式又因为节点A、B相互之间的距离dab已知，联立节点之间的距离方程可以分别求得节点A、B的位置坐标值以及接收机时钟差和

又因为不可收星节点P、Q、S之间的距离及与A、B节点之间的距离都可以通过通信获得，因此，对于节点A与节点P、Q、S的距离方程组为

同理可以列出节点B与节点P、Q、S的距离方程组和P、Q、S之间的距离方程组，从而可以分别求得节点P、Q、S的坐标。至此，全部的可收星节点A、B和不可收星节点P、Q、S的定位完成。

2）当收到的卫星数目M=2，可收星节点数N=3，设不可收星节点数为N′=1（如图2所示）。

假设分别有A、B、C3个节点各自都只能接收到2颗BDS的卫星信号，有节点P由于某些原因无法收到任何卫星信号。设（其中i=a，b，c，p）分别标识节点A、B、C、P节点的3维坐标，C节点的时钟差为tc，同时A、B、C之间的距离为dab、dbc、dac，C和P节点之间的距离为dcp，且都可测量得到。

图2 接收2颗卫星的多点协同定位

根据式（7）可以分别得到节点A、B、C的伪距方程为

在卫星坐标位置矩阵可逆的前提下，由前面算法可以分别得到A、B、C节点坐标值与各节点终端接收机时钟差的关系式和又因为节点A、B、C之间的距离已知，联立关系式和节点之间的3个距离方程，则可以求得收星数都是仅为2颗的3个节点A、B、C的位置坐标值以及各节点终端接收机时钟差。

又因为不可收星节点P和A、B、C节点之间的距离分别可以测量得到，因此根据式（16）可得节点A、B、C与节点P的3个距离方程，从而可以求得节点P的坐标值(xp，yp，zp)。至此，全部的可收星节点A、B、C和不可收星节点P的3维坐标都可以得到，定位完成。

4 结束语

随着卫星导航系统的快速发展，卫星定位也在各行各业诸多领域中得到广泛应用。从单纯依靠卫星导航系统实现户外环境下的定位，到依靠卫星、移动通讯网络等信息载体的融合实现复杂环境下的位置信息获取，为基于位置服务和智慧城市的建设提供必需的数据来源，开创天地一体化、信息融合化、应用智能化、服务泛在化的新阶段。以“协同”学为基础的多点协同定位研究的重点是协同方式和协同内容的研究。在收星条件不佳的情况下，通过待测目标终端节点之间的数据通信实现信息的共享，在满足一定的节点数目条件下是可以实现混合定位目标场景中所有待测点的定位的，而且较其他混合定位方法，本文提出的协同方法因为不用添加额外设备、不用设置标签节点，还具有成本低和定位效率高的特点。下一步还将对多点协同定位的定位精度和可靠度等方面进行深入研究。