数字化变电站无线监测系统信道分析*
2019-06-05何怡刚
黄 炎, 李 兵, 何怡刚
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引 言
数字化变电站具有性能高、安全性高、可靠性高和经济性高的优点,已成为了现在的趋势[1]。无线通信具有覆盖范围广、接入点多、投入及维护成本低、扩展性好等特点,适合在数字化变电站中的控制中心与现场设备之间采用[2]。同时无线通信的传播信道是开放的空间,易受到外界环境干扰,而数字化变电站内存在数量众多的电气设备,且通常为金属材质,金属材质对于电磁波是强反散射体,会改变电磁波的传播路径。因此,有必要研究金属散射体空间分布对于无线信道的影响。
文献[3]从无线通信标准的层面分析无线通信在数字化变电站中的可行性,指出IEEE 802.11标准满足数字化变电站的通信速率要求[3]。文献[4]从安全性角度对无线通信在数字化变电站的运用展开研究[4],给出3种保障信息安全的方法。文献[5]从传输速率和安全性出发,指出无线通信在数字化变电站中的运用前景良好[5]。文献[6]详细介绍了短距离无线通信在数字化变电站中的运用[6],指出其存在电磁兼容问题以及复杂电磁环境下短距离无线通信尚无整体解决方案。文献[7]探讨了无线自组织网在数字化变电站中的自组网结构和路由协议[7]。可以看出,目前学者们的主要研究方向是数字化变电站中无线通信的网络架构、通信协议以及信息安全等问题。而对于数字化变电站这一具体场景中的无线通信信道特性的研究比较少。考虑到数字化变电站复杂的环境条件,有必要研究数字化变电站内散射体的分布对于无线信道特性的影响。
本文根据数字化变电站内发射天线、接收天线以及设备之间的相对位置关系,将数字化变电站划分为斜对角区域、底角区域和中心区域。通过比较数字化变电站不同区域下圆形模型、半圆模型和椭圆模型中到达角的概率密度函数,给出每种模型适用的环境条件,为描述数字化变电站无线通信信道提供了新思路。
1 变电站散射体分布模型
1.1 变电站模型
考虑到实际应用中变电站在选址内部结构与配置方面的特点,本文假设变电站为矩形,控制中心设置在矩形的顶点,发射天线在矩形内部任意位置。散射体分布在矩形区域内,理论计算中不考虑矩形区域以外的散射体影响。为了简化计算,认为散射体是均匀分布的。假设非直达路径的电波传播以在散射体上的单次反射为主,且散射体区域内每个散射体都以恒等于1的相同概率产生一条电波反射路径。假设每个散射体都是全辐射元件,且都具有相同的反射系数。发射天线发射的电波信号经过每个散射体单次反射到接收天线上,如图1(a)所示。
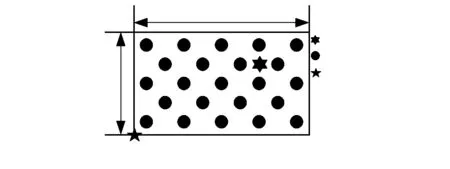
图1 变电站模型
1.2 散射体分布模型与概率密度函数
在二维模型中,接收端到达角度可以用接收天线波达信号方位角来描述。
1.2.1 圆形模型
圆形模型中,发射天线位于圆心位置,接收天线在圆外部,散射体均匀分布在圆形内部,如图2所示。
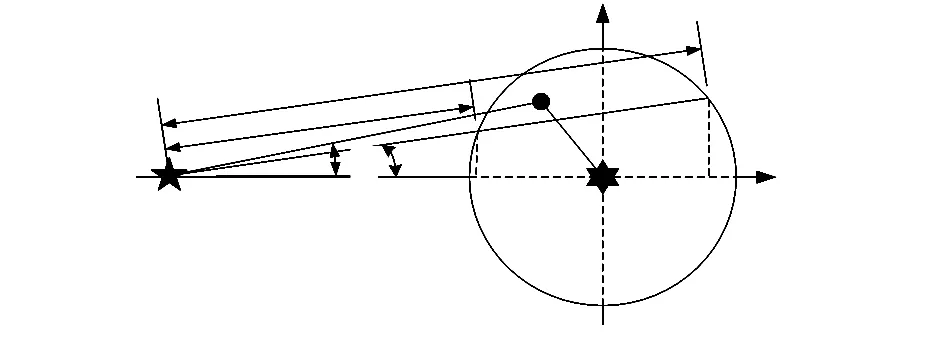
图2 圆形模型示意
接收天线波达信号的方位角为θ,当方位角θ=α时,散射体与接收天线之间的连线会与圆有两个交点,ρ1和ρ2为接收天线到两个交点的距离。根据几何关系可得
ρ1,2(α)sinα=y1,2,ρ1,2(α)cosα=x1,2+D
(1)
式中R为圆形模型中圆的半径,D为数字化变电站内接收天线和发射天线的距离。
接收天线波达信号方位角θ的累积分布函数[8]
(2)
求解关于ρ(α)的一元二次方程组,得到ρ(α)只包含自变量α的表达式,代入式(2)解得
(3)
对累积分布函数F(θ)求关于θ的导数得到方位角的概率密度函数
(4)
式中k=R/D,θ∈[-arcsink,arcsink]。
1.2.2 半圆模型
半圆模型中,发射天线和接收天线分别位于半圆直径的两个端点,散射体均匀分布在半圆内部,如图3所示。
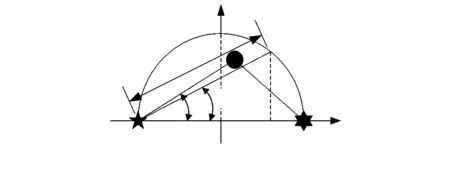
图3 半圆模型示意
接收天线波达信号方位角为θ,当方位角θ=α时,散射体与接收天线的连线与半圆交于一点,ρ为接收天线与该交点的距离。根据几何关系可得
ρ(α)sinα=y,ρ(α)cosα=x+R
(5)
式中R为半圆模型中圆的半径。
接收天线波达信号方位角θ的累积分布函数为[9]
(6)
根据式(5)、式(6)可以解得
(7)
对累积分布函数F(θ)求关于θ的导数得到方位角的概率密度函数
(8)
1.2.3 椭圆模型
椭圆模型中,发射天线和接收天线分别位于椭圆的2个焦点上,散射体均匀分布在椭圆内部,如图4所示。椭圆模型内部散射体关于x轴对称,为了简化计算,先只考虑椭圆上半部分内的概率密度函数。
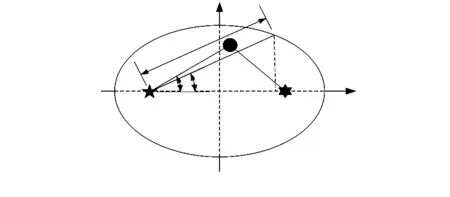
图4 椭圆模型示意
接收天线波达信号方位角为θ,当θ=α时,散射体与接收天线的连线与椭圆有一个交点,ρ为接收天线与该交点的距离。根据几何关系可以得到
(9)
式中a和b分别为椭圆的长半轴和短半轴长度。
接收天线波达信号方位角θ的累积分布函数为[10]
(10)
根据式(9)、式(10)解得
(11)
对累积分布函数F(θ)求关于θ的导数得到方位角的概率密度函数
(12)
式中k=a/b,θ∈[-π,π]。
2 仿真与结果分析
根据数字化变电站内发射天线位置的不同,将变电站划分为几个区域:斜对角区域、底角区域、中心区域,如图5。斜对角区域距离接收天线的距离比较远,周围环境中散射体主要分布在发射天线的周围;底角区域距离接收天线的距离比较远,周围环境中散射体主要分布在发射天线与接收天线连线的一侧;中心区域接收天线的距离适中,周围环境中散射体主要分布在发射天线与接收天线连线的两侧。
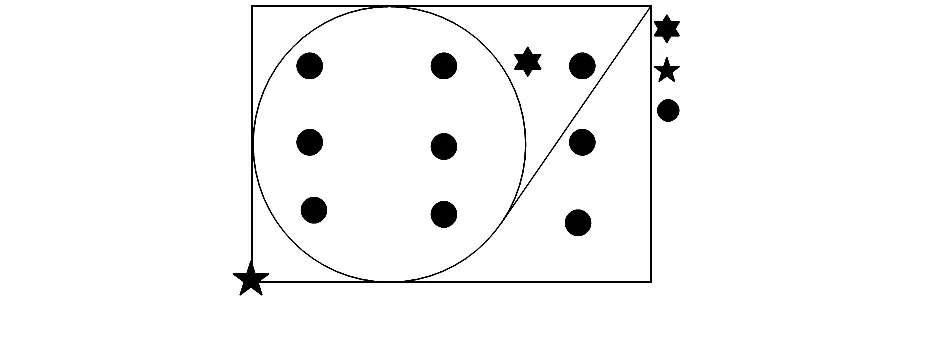
图5 斜对角、底角和中心区域示意
2.1 斜对角区域
数字化变电站内发射天线位于斜对角区域时,散射体分布在以发射天线为圆心的圆内,根据数字化变电站实际环境中散射体的位置以及数量,算出实际环境中接收天线波达信号方位角的概率密度,具体数据如表1所示。

表1 发射天线在斜对角区域时接收端方位角统计数据
根据式(4)、式(8)、式(12)以及表1中的数据画出发射天线在斜对角区域时接收天线波达信号方位角的概率密度函数图像,如图6所示。
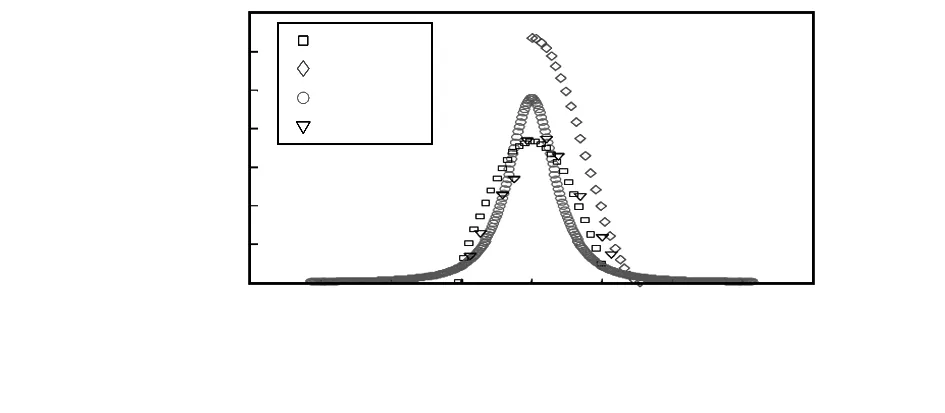
图6 斜对角区域下3种模型的方位角分布
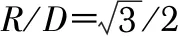
2.2 底角区域
数字化变电站内发射天线位于底角区域时,散射体分布在发射天线与接收天线连线的一侧,根据数字化变电站实际环境中散射体的位置以及数量,算出实际环境中接收天线波达信号方位角的概率密度,具体数据如表2所示。

表2 发射天线在底角区域时接收端方位角统计数据
根据式(4)、式(8)、式(12)和表2中的数据画出数字化变电站内发射天线在底角区域时接收天线波达信号方位角的概率密度函数图像,如图7所示。
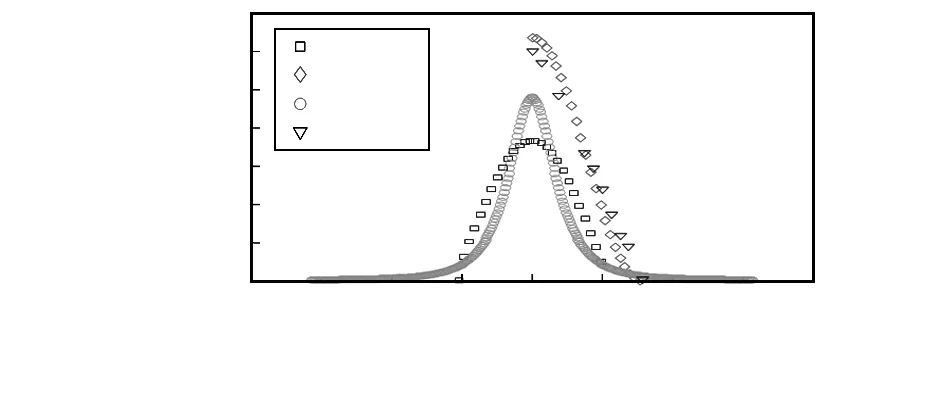
图7 底角区域下3种模型的方位角分布
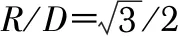
2.3 中心区域
数字化变电站内发射天线位于中心区域时,散射体分布在发射天线与接收天线连线的两侧,根据数字化变电站实际环境中散射体的位置以及数量,算出实际环境中波达信号方位角的概率密度,具体数据如表3所示。

表3 发射天线在中心区域时接收端方位角统计数据
根据式(4)、式(8)、式(12)和表3中的数据画出数字化变电站内发射天线在中心区域时接收天线波达信号方位角的概率密度函数图像,如图8所示。
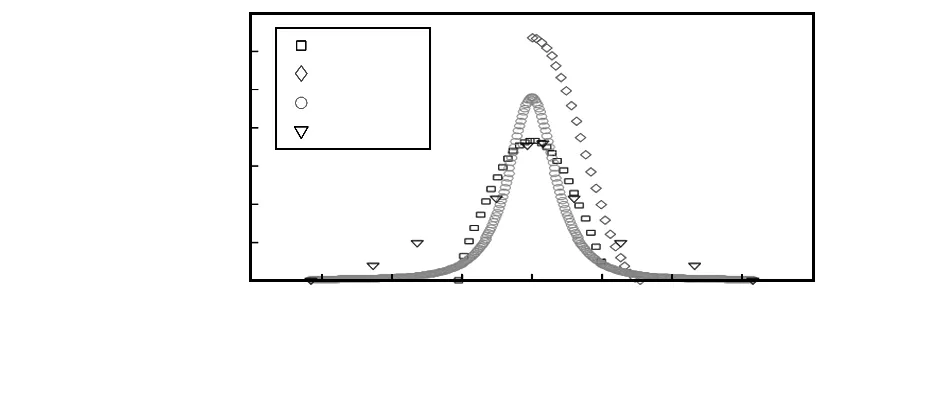
图8 中心区域下3种模型的方位角分布
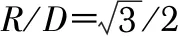
3 结束语
本文依据数字化变电站内发射天线周围散射体的分布规律提出“斜对角区域”、“底角区域”和“中心区域”三个概念。根据数字化变电站内发射天线和接收天线的相对位置关系以及方位角的概率密度函数得出:当发射天线分别位于数字化变电站斜对角区域、底角区域和中心区域时,其对应的散射体分布规律可以用圆形模型、半圆模型和椭圆模型准确描述。本文拓展了空间模型在具体场景下的运用研究。
