不同类型卫星影像区域网平差方法

周平华，李英成，刘晓龙，钱赛男

(1. 江西省地理国情监测遥感院，江西 南昌 330209; 2.中测新图(北京)遥感技术有限责任公司，北京 100039； 3. 中国测绘科学研究院，北京 100830)

随着遥感技术的快速发展，高分辨率卫星在轨数量不断增加，其上的定轨、定姿和授时测量系统等也取得了重大突破[1]。国外，相继发射的SPOT5、IKONOS等卫星，与高精度的定轨及定姿系统(GPS/恒星/惯性组合导航系统)的结合应用，实现了区域范围同轨或异轨立体影像的获取[2]。国内，资源三号卫星的成功发射，提高了我国高分辨率对地观测的能力，促进了基于国产卫星遥感影像的测绘和大比例尺地形图更新的发展[3]。

本文研究了卫星影像的区域网平差方法，该方法利用卫星影像间的连接点进行前方交会、平差，从而有效减少了控制点数量，并大大提高处理效率。通过试验，验证分析不同控制点布设方案下的检查点精度。

1 卫星影像区域网平差

1.1 RFM模型

RFM(rational function model)模型是一种经典的卫星影像成像几何模型，以卫星遥感影像附带的辅助参数为基础，通过拟合获得处理结果，具有平台无关性和良好的内插特性。由于该模型误差在模型估计点之间平滑过渡，因此可根据给定的控制信息，基于控制点、影像之间的约束关系，补偿RFM模型的系统误差，从而提高模型的拟合精度。

RFM模型是将地面点大地坐标D(P,L,H)(经度，纬度，高程)与对应的像点坐标d(s,l)通过比值多项式关联起来。为了增强参数求解的稳定性，通常把地面坐标和像点坐标正则化到(-1.0～1.0)之间。RFM模型表达式如下

(1)

Nums(P,L,H)=a1+a2L+a3P+a4H+

a5LP+a6LH+a7PH+a8L2+a9P2+a10H2+

a11LPH+a12L3+a13LP2+a14LH2+a15L2P+

a16P3+a17PH2+a18L2H+a19P2H+a20H3

(2)

Dens(P,L,H)=a21+a22L+a23P+a24H+

a25LP+a26LH+a27PH+a28L2+a29P2+a30H2+

a31LPH+a32L3+a33LP2+a34LH2+a35L2P+

a36P3+a37PH2+a38L2H+a39P2H+a40H3

(3)

式中，三次有理多项式Nums(P,L,H)、Dens(P,L,H)、Numl(P,L,H)、Denl(P,L,H)由RPC参数和大地坐标D(P,L,H)对应的像点坐标d(s,l)组成。多项式中，一次多项式表示光学投影系统产生的误差；二次多项式表示地球曲率、大气折射和镜头畸变等产生的误差；三次多项式表示由于相机震动等产生的一些未知的、具有高阶分量的误差。

1.2 基于仿射变换的RPC参数精化

在RFM模型参数求解时，常加入一定数量的地面控制点来提高RFM模型的精度。常用的参数求解方法有两种，第一种方法是利用大量地面控制点直接对RPC参数进行校正。由于RPC参数间相关性不确定，在实际应用中难以实现。第二种方法是利用稀少的地面控制点和适当的联结点解算影像的仿射变换参数。这种方法只需少量控制点，而且不需要校正RPC参数，计算简单。因此，本文在对RPC参数求解时采用了第二种方法。具体步骤如下：①量测控制点的像点坐标；②利用RFM模型分别计算控制点对应的像点坐标；③利用前方交会计算连接点对应的物方坐标，利用RFM模型计算连接点对应的像点坐标；④利用控制点的量测像点坐标，以及连接点匹配得到的像点坐标、RFM模型计算的像点坐标分别构建仿射变换公式，联合解算仿射变换参数。仿射变换公式定义如下

x+f0+f1y+f2y-RPCx(P,L,H)=0

(4)

y+e0+e1y+e2y-RPCy(P,L,H)=0

(5)

式中，(x,y)为控制点在影像上的像平面坐标；(f0,f1,f2,e0,e1,e2)为仿射变换参数。式(1)中的RFM模型参数为卫星遥感影像严格成像模型的系统参数。

按泰勒级数展开得到连接点线性方程，以矩阵形式表示为

V=AΔ+lp

(6)

式中

(7)

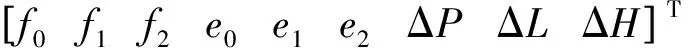
(8)

(9)

(10)

(11)

(12)

(13)

3a12L2+a13P2+a14H2+2a15LP+2a18LH

(14)

a33P2+a34H2+2a35LP+2a38L2H

(15)

a15L2+3a16P2+a17H2+2a19PH

(16)

2a17PH+a18L2+a19P2+3a20H2

(17)

(18)

每个控制点和连接点都可列出一组如式(6)所示的误差方程，再根据最小二乘法原理将误差方程转化为法方程(如式(19)所示)，并解出成像模型参数(f0,f1,f2,e0,e1,e2)。

(ATA)Δ=ATl

(19)

根据成像模型求解的RPC参数的精度与成像模型的精度一致。当有1个控制点时，求解影像与地面间的平移参数(f0,e0)只能消除平移误差；当有2个控制点时，可求解平移参数(f0,e0)和影像行方向的纠正系数(f1,e1)。对于单线阵推扫式卫星遥感影像而言，行方向(CCD线阵)的变形较列方向(卫星运动方向)的变形小，因此利用2个控制点就可以得到较高的精度。

1.3 基于RFM模型的卫星影像前方交会

由两张卫星影像匹配得到的连接点，需要利用基于RFM模型的卫星影像前方交会法计算其物方坐标，进而加入到区域网平差模型中。

左、右影像的有理多项式系数分别为RPC和RPC′，地面点在左、右影像上的行列值坐标分别为(ROWl,COLl)和(ROWr,COLr)，根据影像像素坐标标准化公式可以得到标准化之后的行列值坐标(rl,cl)和(rr,cr)，则有

Fs=Nums(P,L,H)-sDens(P,L,H)=0

(20)

Fl=Numl(P,L,H)-lDenl(P,L,H)=0

(21)

对Fs取全微分，得到线性化之后的RPC模型为

(22)

(23)

式中

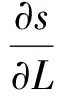
(24)

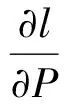
(25)

对左、右影像的RPC参数分别进行线性化，取全微分则可以得到下列方程组

(26)

写成矩阵形式，其误差方程式为

(27)

(28)

在建立立体影像的空间前方交会模型时，由于左、右影像RPC系数不同，其各自的标准化参数也不同，加之左、右影像的标准化参数各不同，从而导致左、右影像所对应的标准化之后的物方空间坐标(X,Y,H)在表达形式上也存在差异，因此不能直接对误差方程式解算求出(P,L,H)。考虑到形式统一，需要将物方空间未标准化的原始坐标(Pu,Lu,Hu)代入到方程组中计算，而不是直接用标准化坐标(X,Y,H)计算，从而避免左、右影像标准化坐标不一致的现象。

假设(Pu,Lu,Hu)是未标准化的物方空间坐标，(P0,L0,H0)是标准化参数中的偏移因子，(Pk,Lk,Hk)是标准化参数中的比例因子。用原始物方空间坐标代替标准化坐标之后，左、右影像各自线性化之后的RPC参数如下

(29)

方程组的误差方程式如下所示

(30)

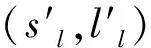
(31)

由于采用原始物方空间坐标代替标准化坐标，因此误差方程式的系数矩阵中的各项线性化系数也发生了改变。

2 试验与结论

选取河北保定地区八景遥感影像进行区域网平差试验，影像分布如图1所示。

每2景影像重叠区匹配得到的同名点可作为连接点，3度重叠区则相应匹配得到了三度重叠点。

单景影像选取了10个左右控制点，但两景之间重叠区均未选取控制点，因此需要选择更多的控制点。

控制点布设方法包括以下3种方案：方法1中每张影像布设5个控制点，分布在影像四角和中心；方法2中每张影像布设4个控制点，分布在影像四角；方法3则根据空间分布进行布点，中间片至少1个点，四角片至少3个点，剩余控制点作为检查点用于分析评价每种方案的结果精度。结果精度分析见表1。

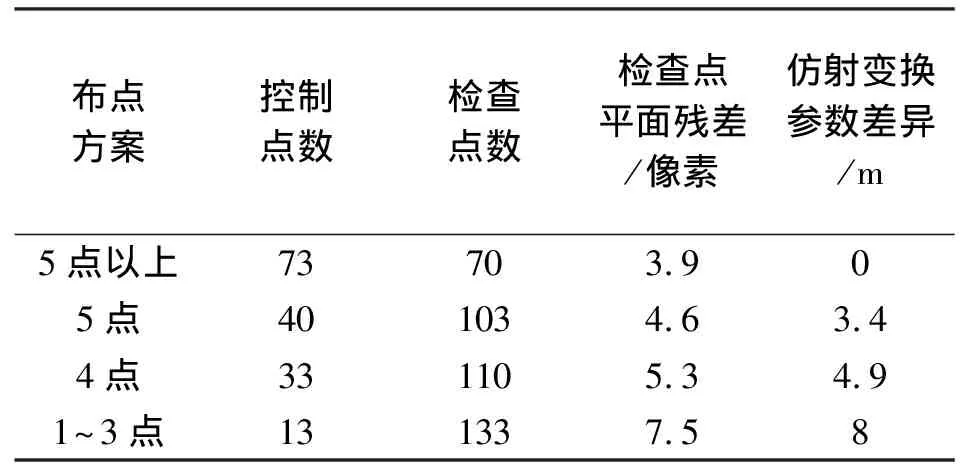
表1 精度分析对比

通过表1试验结果可以看出：当每片控制点降到4个时，结果比较稳定；每片控制点降到3个时精度略降低。因此通过区域网平差，至少可以减少一半的控制点数量，同时减小了重叠区的连接点误差。可以通过试验进一步研究定向点及平面控制点对区域网平差的作用，从而更有效地减少外业控制点数量，提高区域网平差的效率。

3 结 语

本文通过区域网平差方法，利用影像间的多度连接点进行RPC模型的前方交会，并用稀少控制点进行仿射变换，实现了多轨多景卫星影像几何纠正。经试验测试，可减少一半以上单景纠正时需要的外业控制点，极大地提高了卫星影像正射纠正效率。

由于本文试验数据有限，控制点选取的合理性尚有不足，下一步有待通过更加系统的试验进行验证。