高静低动隔振系统的双时延反馈混沌化

2019-06-04楼京俊杨庆超

船舶力学 2019年5期

柴凯，楼京俊，杨庆超，俞翔

（海军工程大学a.舰船与海洋学院；b.科研学术处，武汉430033）

0 引言

舰船动力机械周期性运转产生的水下辐射噪声主要有两个危害，其一是线谱特征，其二是线谱强度，利用非线性隔振系统处于混沌状态时其响应功率谱呈连续谱的特点，可以改变和重构动力机械振动传递到艇体基座的线谱特征，提高舰船的声隐身性能。朱石坚等[1]系统地提出了线谱混沌化控制方法；楼京俊等[2]深入研究线谱混沌化的基本原理，提出了Duffing 隔振系统的性能评估指标，通过实验证明了混沌隔振原理的有效性；俞翔等[3]采用数值仿真和实验方法研究了非线性隔振系统在混沌状态的隔振性能；刘树勇等[4]对准周期激励非线性隔振系统的混沌进行了研究。基于混沌的隔振系统研究重点和难点在于如何实现小振幅、宽频域和持续的混沌，很多学者开展了非线性系统的混沌化技术研究。张振海等[5]利用Lyapunov 指数配置，提出了离散脉冲混沌化方法；曾强洪等[6]对投影混沌同步在隔振系统中的应用进行了深入研究；张敬等[7]提出了非线性时延反馈控制的混沌化方法；李盈利等[8]利用时延反馈实现了双层非线性隔振系统的持续小振幅混沌化。混沌化方法虽然能有效改变线谱特征，但在削弱其线谱强度上作用不大，降低动力机械振动向船体传递最有效的方法是提高隔振系统的隔振性能。高静低动隔振系统是一种将正负刚度弹性元器件并联在静平衡位置获得低刚度的组合隔振系统，能有效解决大承载力和超低频隔振、超低刚度和位置稳定性、低频振动传递率和高频振动衰减率不可兼顾的矛盾，具有高的静载支撑能力和低频隔振性能，且有利于实现小能量混沌化控制，引起了诸多学者极大的关注。郑宜生等[9]对基于永磁铁和电磁铁的高静低动隔振器进行了深入研究；Zhou 等[10]通过电磁铁、永磁体和屈曲梁得到了半主动的高静低动隔振系统；孟令帅等[11]研究了等厚和变厚蝶形弹簧提供负刚度的高静低动隔振系统。高静低动隔振器负刚度实现机制主要有以下三种形式：（1）储备了一定能量或发生了一定形变的机构；（2）几何非线性机构；（3）微小扰动后能减小回复力的机构。本文通过双时延反馈控制实现高静低动隔振系统的混沌化，实现线谱混沌化控制技术与舰船动力装置隔振的有机结合，达到了降低线谱强度和隐匿线谱信息的双重目的。

1 系统建模和问题描述

1.1 高静低动隔振系统动力学建模

典型三弹簧高静低动系统的原理如图1所示。主要由一根正刚度竖直弹簧和两根完全相同的负刚度斜弹簧组成，其中竖直弹簧刚度为k2，斜弹簧刚度为k1，三根弹簧的一端在C 点连接，另一端分别铰接在A、B 和O 点；斜弹簧水平时的长度a，此时竖直弹簧处于静平衡位置，相应压缩量为h，x 表示系统在外力f 作用下产生的位移。

在外力f 作用下，高静低动系统在竖直方向上的力：

设y=x-h，并将（1）式无量纲化可得

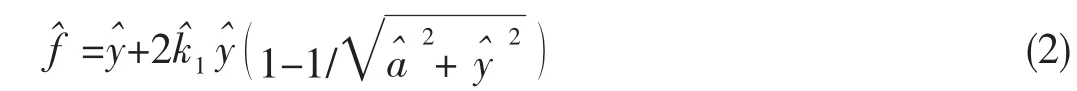
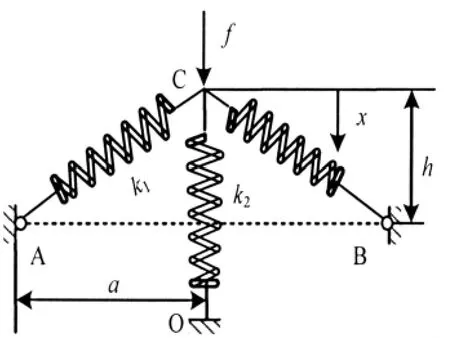
图1 高静低动隔振系统的结构示意图Fig.1 Schematic representation of an isolator based on HSLDS

（2）式依据三阶Maclaurin 公式展开，可得

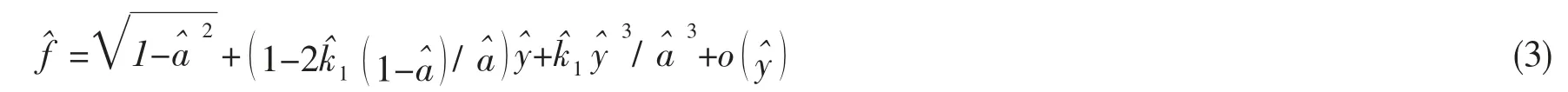
因此，水平弹簧不仅能够降低系统的正刚度，从而减小系统的固有频率，扩大隔振频带的宽度；而且能够产生非线性立方刚度，具有硬弹簧的特性，从而使系统的共振曲线骨架向高频弯曲，发生共振频率转移现象。

1.2 双时延反馈控制的高静低动隔振系统动力学建模

考虑的高静低动隔振系统，控制器设计为含有位移和速度的双时延反馈控制器，具体如图2所示。被隔振物体质量为M，它由一个含一次刚度系数k1和三次刚度系数k3的弹簧和一个线性阻尼组成的隔振器支撑，在被隔振物体和基座之间有两个作动器，用来施加双时延反馈控制，Kt1和Kt2分别为位移和速度反馈的控制增益，τ1和τ2分别为位移和速度反馈的延迟时间，且τ1=τ2。

M 处于静平衡位置时弹簧压缩量为h，令X=Z-h，在简谐力Fcos（ωnt）激励下，系统动力学方程为：

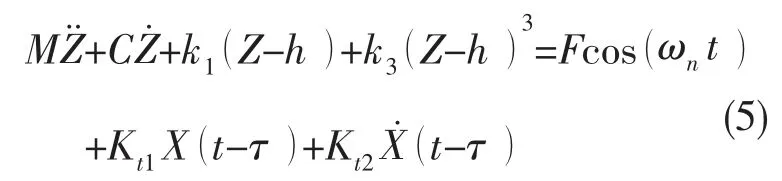
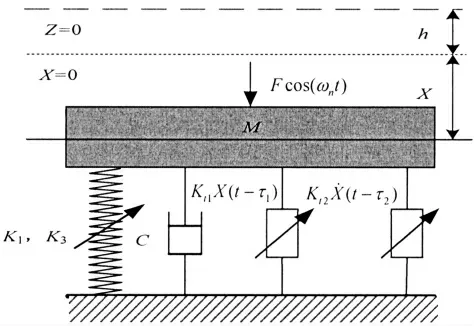
图2 双时延反馈控制的高静低动隔振系统模型Fig.2 Vibration isolation system based on HSLDS with dual time-delay feedback control

其中：Mg=k3h3-k1h，则（5）式可进一步改写为

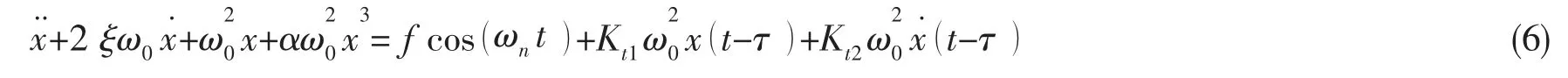
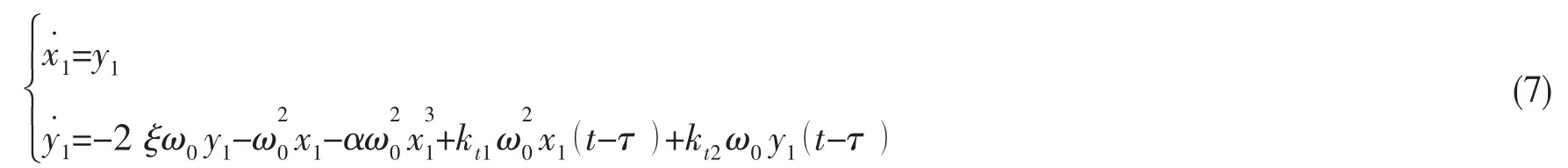
在kti=0（i= 1，2）时，求得（7）式的平衡点A（0，0）。为了分析（7）式在平衡点附近的稳定性，在A 点处施加一个无限小的扰动（Δx1，Δy1），则其满足如下线性化方程：

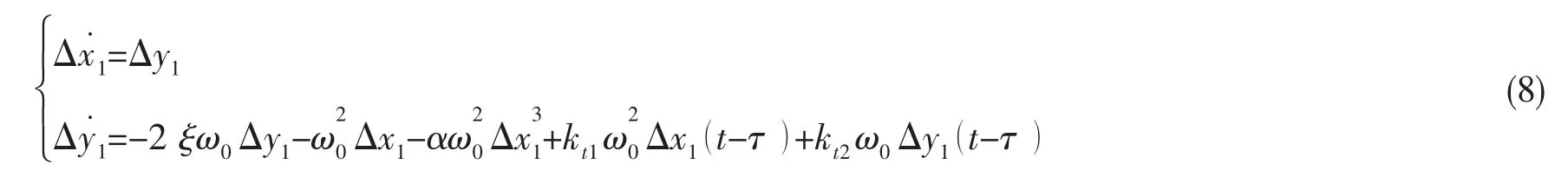
2 稳定性分析

系统稳定性分析主要分为全时延稳定性和稳定性切换。系统全时延稳定是指对于任意给定的时延τ 系统均稳定[12]；而在实际系统中，系统全时延稳定的控制增益区间较小，实际控制增益常位于全时延稳定区域之外。稳定性切换是指当控制增益位于全时延稳定区域之外时，随着参数的变化，系统稳定性会有由不稳定变为稳定，或者由稳定变为不稳定的现象[13]。

线性时延系统（8）的特征方程为：

定理1：方程（8）零解全时延稳定当且仅当它满足以下两个条件：

（1）当τ=0 时，P（λ）+Q（λ）是Hurwitz 稳定的；

（2）对于所有的τ≥0，D（iω ，τ）=0 无非零实数根ω。

当τ=0 时，由Routh-Hurwitz 稳定性判据可知系统零解全时延稳定应满足kt1＜1，kt2＜2ξ。在上述前提下，假设式具有纯虚根λ=iω（ω≥0），则有

分离（10）式的实部和虚部，可得关于谐波函数的方程组：

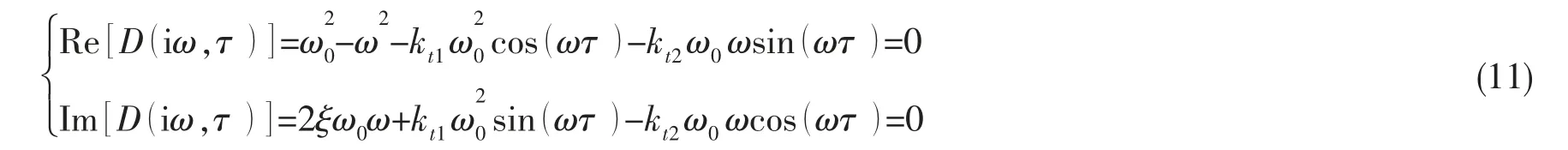
由此得到：

消去方程（12）中的谐波项，可得一个关于ω 的四次代数方程如下：

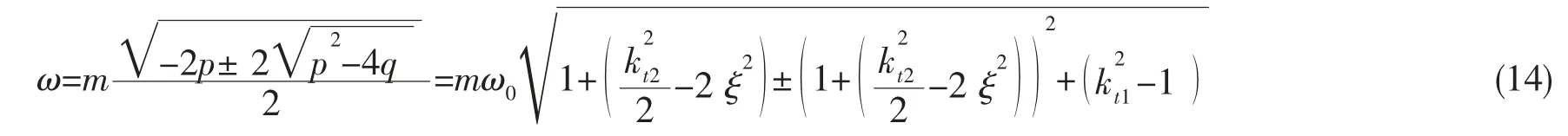
根据不同的参数组合形式，可以得到D（iω ，τ）=0 无正实根的条件为：p≥0，q≥0 或p＜0，p2-4q＜0，即：

由（14）式可知方程（10）最多有两个正实根ω1和ω2，将其代入（12）式可求出两组临界时延：

其中：c=1，2，k=0，1，2，L，arccos（·）是反余弦函数。

特征根λ 是时延τ 的函数，求出一对纯虚根±iωc和相应临界时延τk后，纯虚根的变化趋势就可由确定，其中sgn 为符号函数。在ω1和ω2处，有

采用如下定理[15]分析系统的稳定性切换：

定理2：假设P（iω）和Q（iω）无公共实根，且P（0）+Q（0）≠0，且F（ω）=0 无非零重根，则有：

（1）若F（ω）=0 无实根或仅有零根，则系统稳定性与无时延时的稳定性一致；

（2）若F（ω）=0 仅有1 个正单根，且τ=0 时稳定，存在临界时延τ0，使得系统在τ∈[0，τ0）内稳定，而τ≥τ0时不稳定，发生一次稳定性切换；而τ=0 时不稳定，则系统全时延不稳定；

（3）若F（ω）=0 有两个或两个以上的正实根，随着τ 的增大，发生有限次数的稳定性切换，最终系统不稳定。

表1 不同参数组合下临界时延的计算公式Tab.1 Computational formula of critical time delays with different parameter combinations

3 数值仿真与分析

将无量纲控制增益kt1、kt2和τ 作为控制参数，若无特殊说明，设定系统的参数为：ξ=0.2，ω0=1，α=0.1，初始条件为（0.001，0）。为验证稳定性分析结论的准确性，进行下列算例仿真。

算例①：kt1=-1.5，kt2=0.1

F（ω）=0 有一个实根ω2=1.541 5＞ω0，且满足F′（ω2）=8.947 1＞0，相应临界时延为：

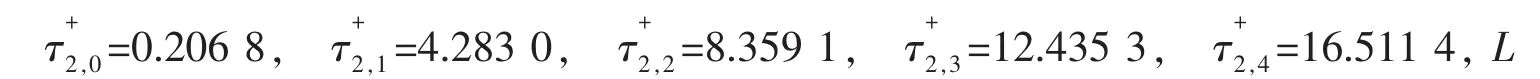
算例②：kt1=-0.5，kt2=0.1

F（ω）=0 有两个不同实根ω1=0.776 4＜ω0＜ω2=1.118 0，且F′（ω1）=-1.007 0＜0，F′（ω2）=1.435 4＞0，相应临界时延和为：

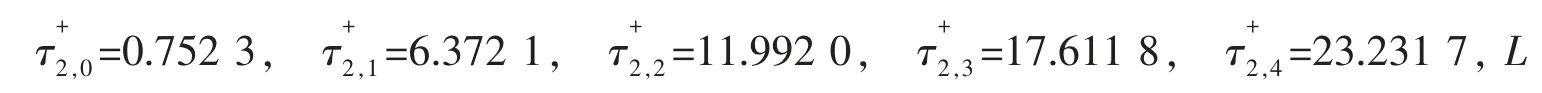
图3 隔振设备的响应（kt1=-1.5，kt2=0.1）Fig.3 Response of the isolated equipment when kt1=-1.5 and kt2=0.1

图4 隔振设备的响应（kt1=-0.5，kt2=0.1）Fig.4 Response of the isolated equipment when kt1=-0.5 and kt2=0.1

算例③：kt1=0.1，kt2=0.1

易知kt1=0.1 和kt2=0.1 满足全时延稳定性条件：，因此系统对任何时延均稳定。高静低动隔振系统的响应如图5所示，由图可知，系统在τ=4.5、τ=7.5 和τ=12.5 时均稳定。

图5 隔振设备的响应（kt1=0.1，kt2=0.1）Fig.5 Response of the isolated equipment when kt1=0.1 and kt2=0.1

4 双时延反馈混沌化

稳定性分析表明，通过调整控制增益和时延，可以使高静低动隔振系统稳定或者失稳。设谐波力激励的幅值f =0.5，ωn=3，隔振系统的参数为ξ=0.2，ω0=1，α=0.1，下面分析时延τ、位移控制增益kt1和速度控制增益kt2对系统混沌化控制的影响，对系统混沌化过程中控制参数进行优化。图6（a）是kt1=-1.5，kt2=0.1 时系统响应随时延变化的分岔图，无特殊说明，云点代表混沌运动或准周期运动，单线点或多线点代表周期运动。由图可知，系统在τ=0.2 时第一次发生Hopf 分岔，这与算例①的临界时延吻合，当时，系统作持续的混沌运动；图6（b）是kt1=-0.5，kt2=0.1 时系统响应随时延变化的分岔图，由图可知系统周期与混沌运动交替出现，出现阵发性混沌，这与算例②的稳定性切换结论一致；图6 表明：不稳定区域相比稳定区域，更容易实现时延混沌化；较大的时延可以降低混沌响应峰值。

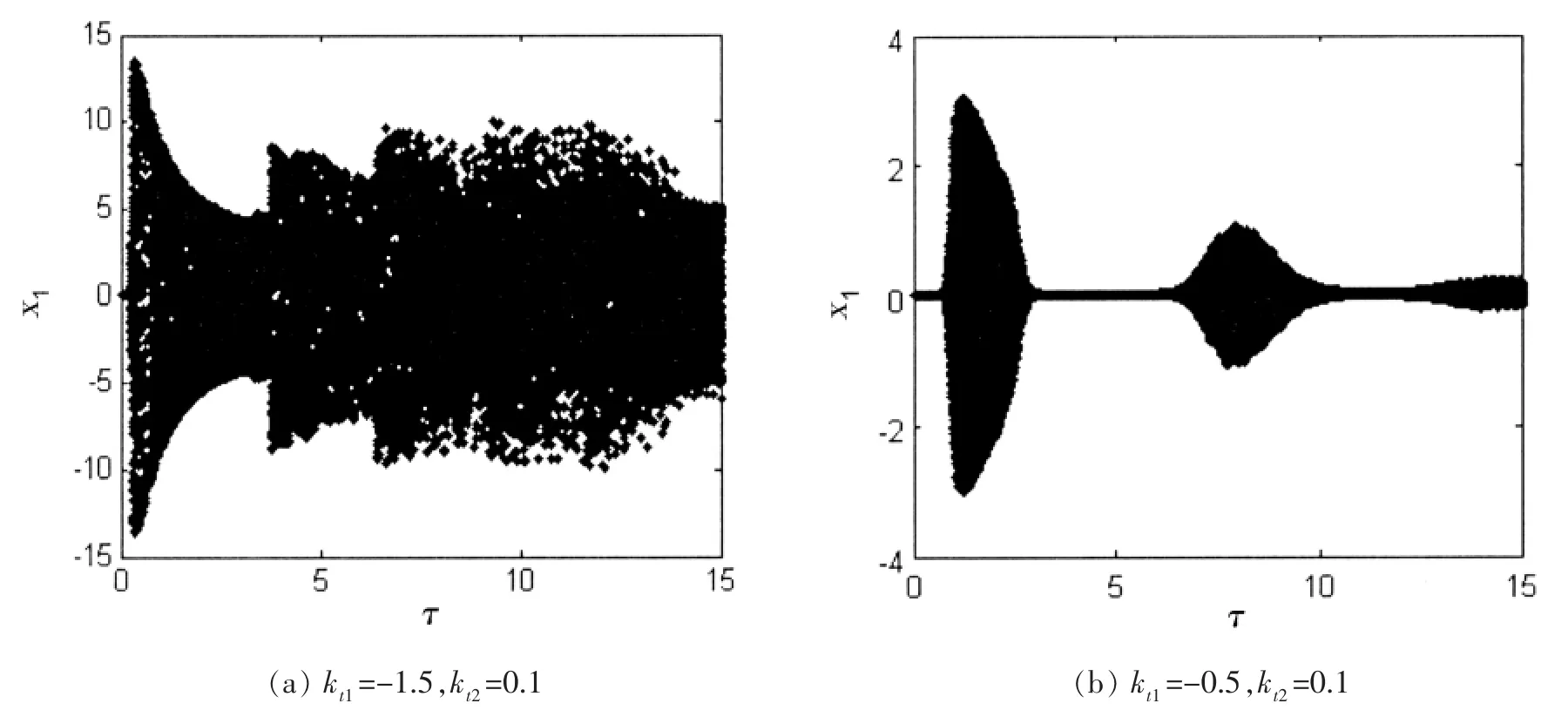
图6 关于时延τ 的分岔图Fig.6 Bifurcation diagrams of the HSLDS-VIS with the time delay τ

图7 是时延取τ=50 时系统随控制增益的分岔图，由图可知：正反馈（kt1＞0）可以降低系统响应幅值。图7（a）中kt2=0.1，kt1∈[-2，2]，由图可知：当控制增益位于全时延稳定区域时，即使时延取较大值，系统也未出现混沌；图7（b）中kt1=kt2=k，kt∈[-2，2]，由图可知：含时延位移和时延速度的双时延反馈高静低动隔振系统相比仅含时延位移反馈的高静低动隔振临界控制增益更小，混沌云点更稠密，表明双时延反馈控制器更容易实现系统混沌化，且混沌化品质更高。

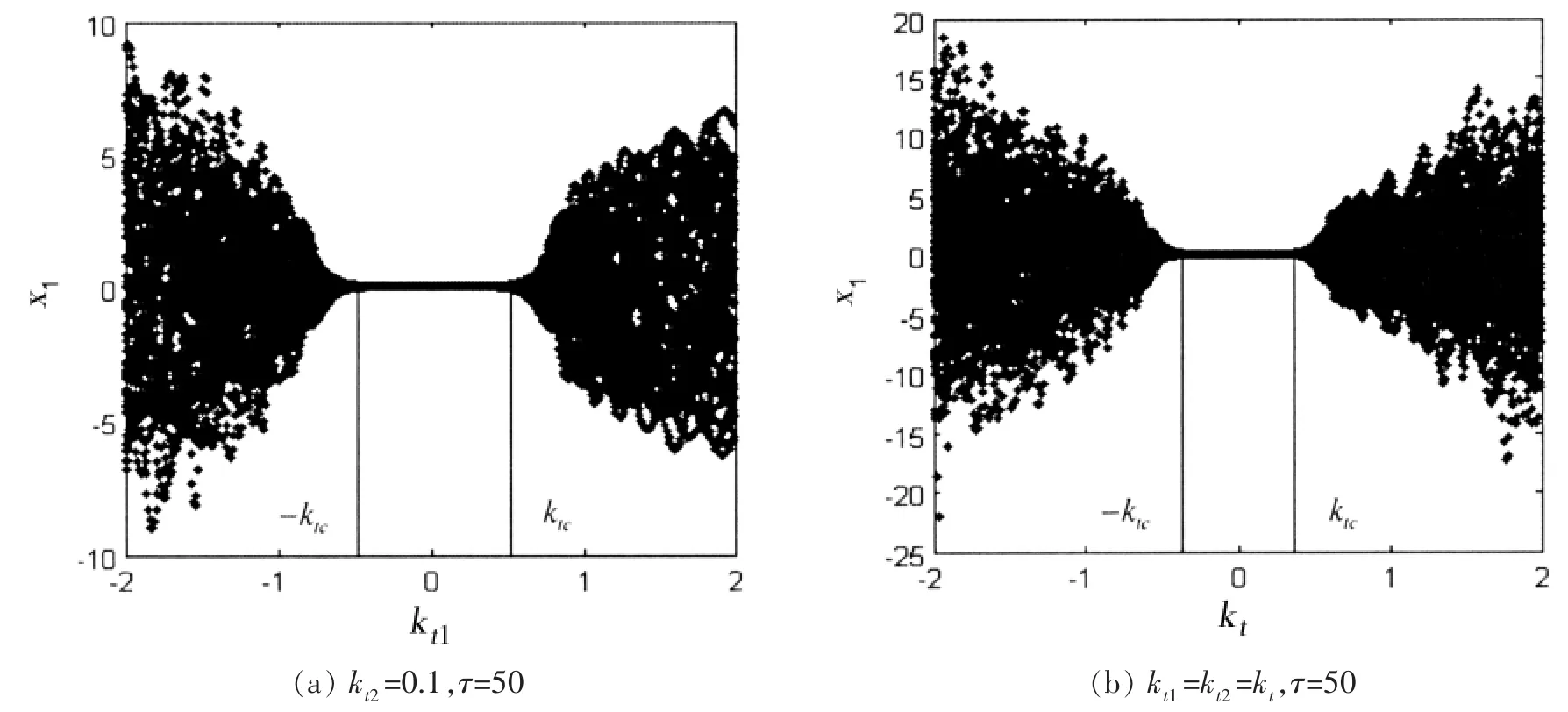
图7 关于控制增益kt 的分岔图Fig.7 Bifurcation diagrams of the HSLDS-VIS with control gain kt

图8 是不同时延和不同控制增益隔振设备的相图，当时延控制参数在全时延稳定区域时，系统对应周期运动图8（a）或准周期运动图8（c），当时延控制参数在不稳定区域时，系统对应混沌运动图8（b）和图8（d）。

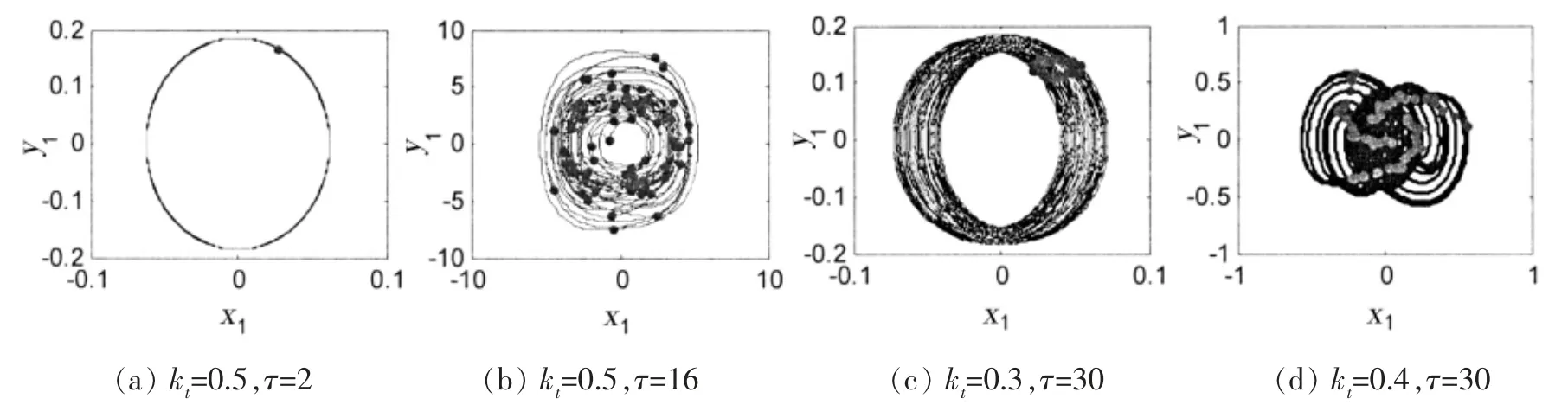
图8 隔振设备的相图Fig.8 Phase diagrams of the isolated equipment

图9 不同系统的功率谱对比Fig.9 Comparison of the power spectra with the different systems

图9 是不同系统双时延反馈控制时的功率谱对比，由图9（a）可知，未受控系统作周期运动，最高线谱位于2.997 Hz 处，幅值为1.596 dB；施加控制后的一般非线性系统和高静低动系统，特征线谱变为连续的响应功率谱，说明施加双时延反馈进行线谱混沌化是有效的；图9（b）和（c）对比可知，一般非线性系统功率谱峰值为8.31 dB，而高静低动隔振系统的功率谱峰值为-3.75 dB。因此，相比一般非线性隔振系统，高静低动隔振系统混沌化所需控制增益小，低频隔振性能更优越，使得双时延反馈控制的高静低动隔振系统不仅能改变线谱特征，而且可以降低线谱强度，具有更好的混沌化效果。