船舶辅机浮筏半主动非线性隔振系统振动特性分析
2019-06-04方媛媛夏兆旺Waters左言言
方媛媛,夏兆旺,Waters T P,左言言
(1.江苏大学 汽车与交通工程学院,江苏 镇江212013;2.江苏科技大学 能源与动力学院,江苏 镇江212003;3.Institute of Sound and Vibration Research,University of Southampton,SO17 1BJ,UK)
0 引言
船舶动力机械运行引起的振动不仅使船体结构和设备产生疲劳损坏,影响声呐等精密仪器设备的正常工作,也会使舰船、特别是潜艇的水下辐射噪声增大,降低舰船的隐身性能[1-3]。采用隔振装置将船舶设备进行弹性安装,是舰船减振降噪最常用的技术手段之一[4-6]。
为了进一步提高船舶动力装置的减振降噪效果,在传统单层隔振和双层隔振的基础上,发展了浮筏隔振技术,其作为一种有效的舰船设备隔振装置已经在多种船型上得到广泛使用[7-9]。浮筏技术的采用使得国内外舰艇的隐身性能不断取得进展,目前浮筏系统面临着如何将其隔振效果继续提高的问题。过去的仿真及实验研究表明,被动隔振装置可以降低全频段振动总量级,但很难消除低频振动。因此各国学者开始进行船舶动力机械的主动隔振[10]、半主动隔振[11-12]及主被动联合隔振装置[13-14]的研究。其中半主动隔振技术因为其能耗低、响应迅速、价格低等优点而被广泛使用。磁流变阻尼器是一种典型的半主动隔振装置,在汽车、机械装置、桥梁以及土木建筑等领域得到广泛应用,并展现出了良好的应用前景[15-18],一些学者也探索了其在船舶隔振领域的应用[19]。
本文以基于磁流变阻尼技术的船舶辅机半主动浮筏隔振系统为研究对象,以含滞后特性的改进的Bingham 模型[20]描述磁流变阻尼器的阻尼力,进而建立了含磁流变阻尼器的船舶辅机浮筏半主动隔振系统的非线性动力学方程,采用平均法分析了系统的稳态响应,并通过数值模拟方法验证了平均法的正确性。以力传递率为评价指标,研究了半主动隔振系统的参数对隔振效果的影响规律,为船舶辅机非线性半主动系统的隔振设计奠定了基础。
1 浮筏半主动隔振系统动力学模型
本文采用两台船舶动力机械共用一个中间质量,浮筏半主动非线性隔振系统如图1所示,系统的动力学方程为
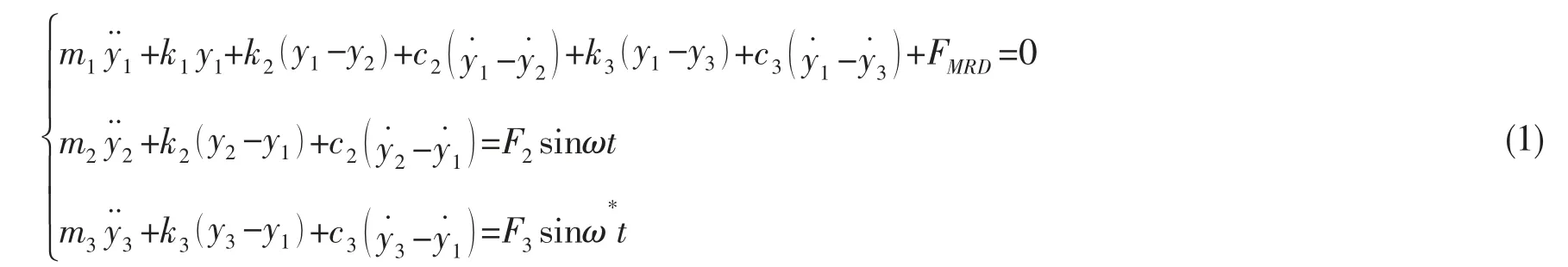
式中:m1、m2、m3分别为筏架和上层动力机械设备的质量;y1、y2、y3分别为m1、m2、m3的垂向位移;k1、k2、k3分别为支撑m1、m2、m3的隔振器刚度;c2、c3分别为机组下的隔振器阻尼;F2sinωt 和F3sinω*t 为动力机械设备激振力;FMRD为磁流变阻尼器的阻尼力。
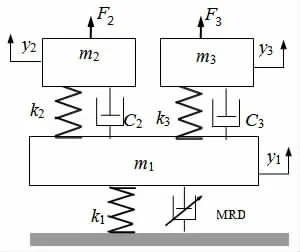
图1 船舶浮筏半主动隔振系统Fig.1 Floating raft semi-active isolation system for ship
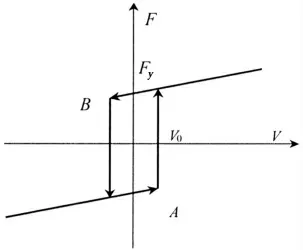
图2 MR 阻尼器的修正Bingham 模型Fig.2 The revised Bingham model of MRD
采用改进Binghan 模型描述磁流变阻尼控制系统的滞后特性,如图2所示,其表达式为

式中:Fy为控制力,V0为磁流变阻尼器的零力速度,c1为磁流变阻尼器粘性阻尼系数。
2 浮筏半主动隔振系统的力传递率
取无量纲位移x1=y1k2/F2,x2=y2k2/F2,x3=y3k2/F2,γ= ω*/ω,无量纲时间τ= ωt,对(1)式进行无量纲化可得
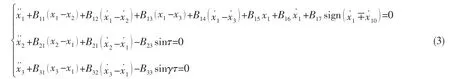
为了对浮筏隔振系统的振动传递特性进行数值和解析研究,可以将(3)式变换成一组一阶微分方程组的形式:
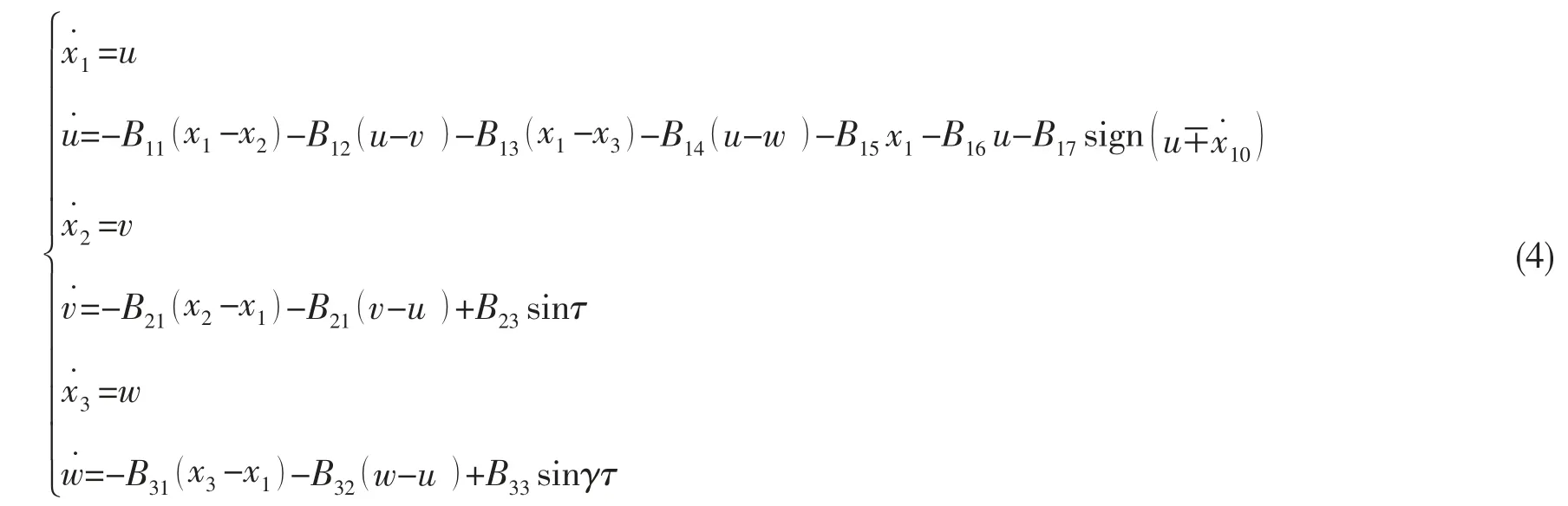
如果(4)式中非线性系数B17与其它项系数相比是小值,那么该系统是弱非线性系统。用非线性振动理论中的平均法求解系统主共振响应,设其解为

式中:φi=τ-θi,ai为系统响应的幅值,θi为响应的相位。根据平均法的假设,(5)式可以转换为

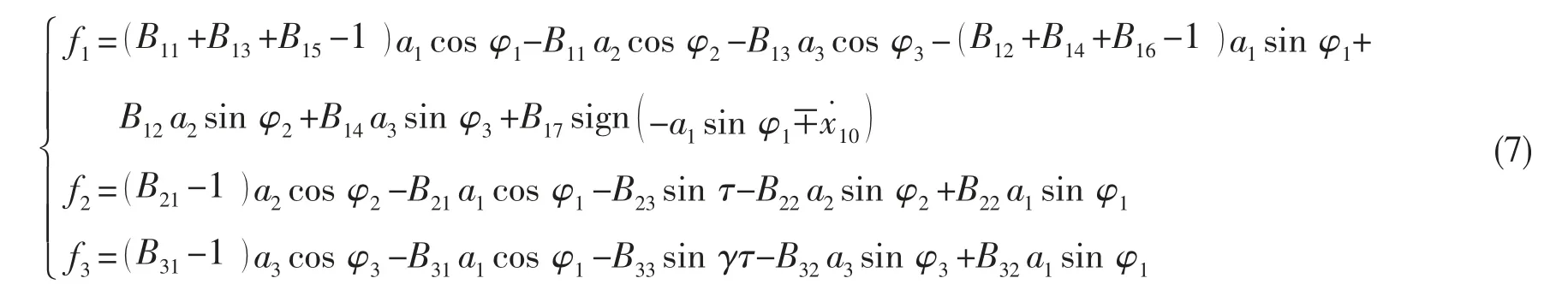
由(6)式可解得
李克强总理在今年4月27日国务院第一次廉政工作会议上说,公共工程事关国计民生,决不能把民生工程搞成劳民伤财沽名钓誉的“形象工程”和“政绩工程”。如果一些地方能够多关心百姓民生,多了解民间疾苦,恐怕就不会有那些只顾形象与政绩的工程了。

对(8)式进行K-B 变换,利用φ1-φ2=θ2-θ1,并将其在[0,2π]上平均积分,可得系统响应幅值和相位的时间变化率的表达式:

式中:
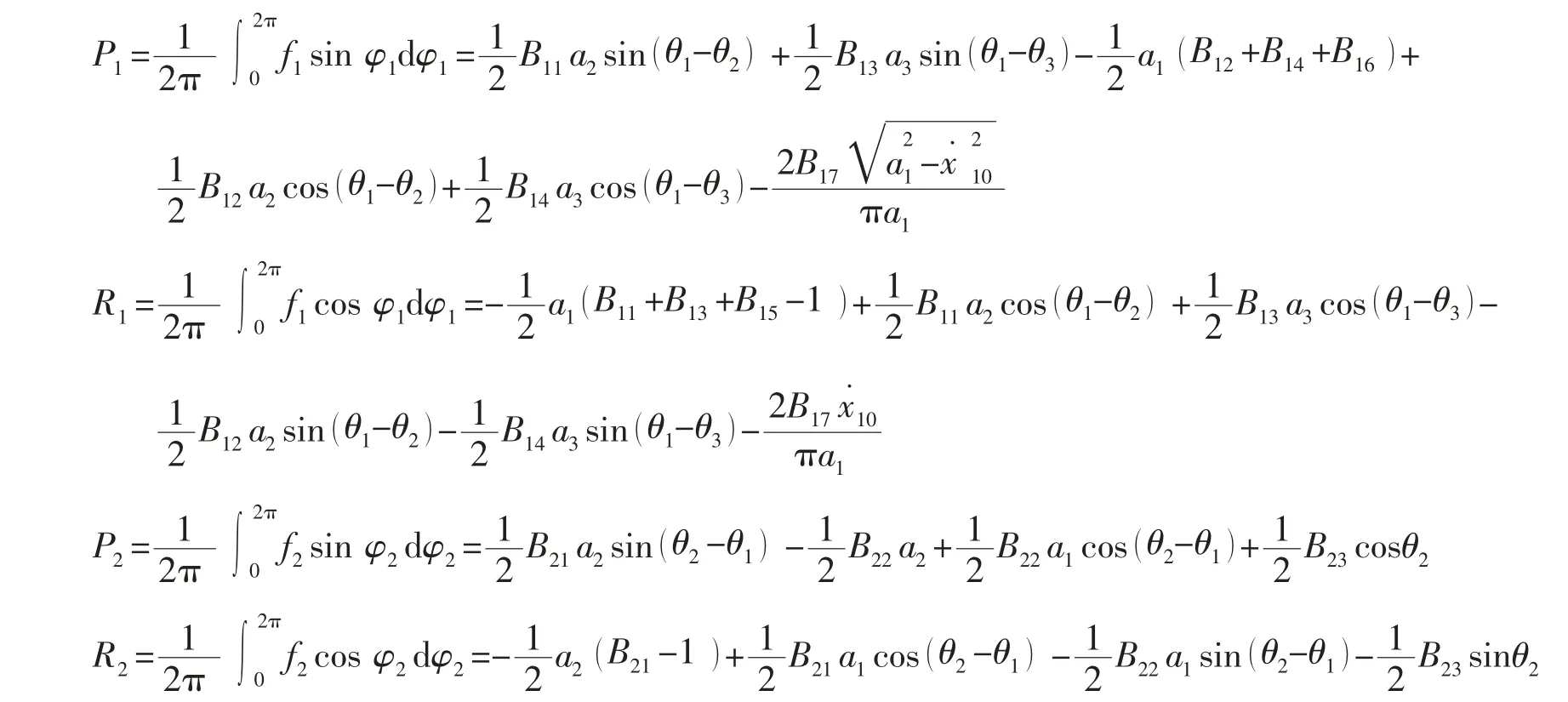
当ω*= ω,即γ=1 时,
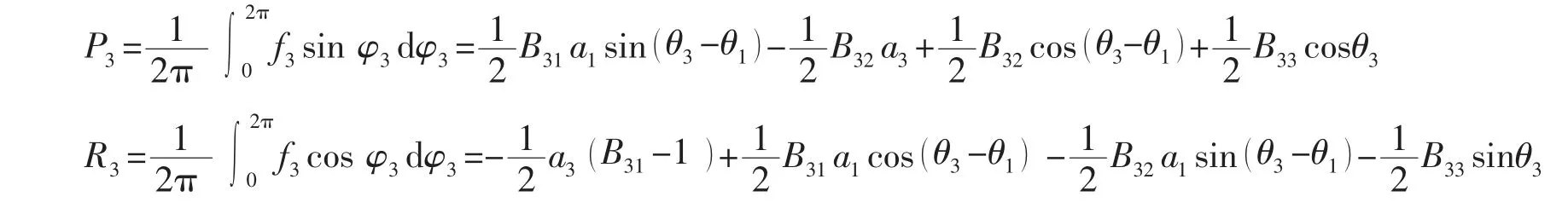
当ω*≠ω,即γ≠1 时,
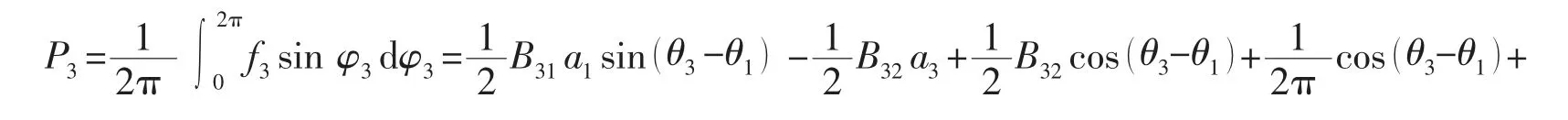
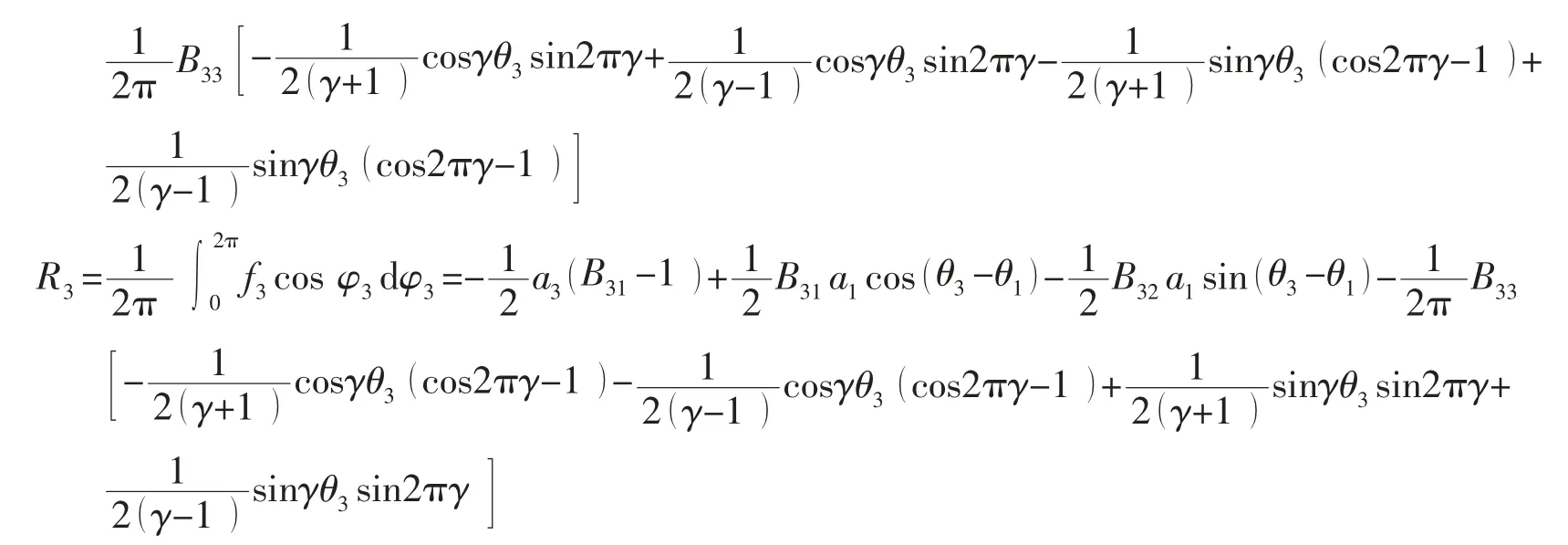
平均法用于求解非线性方程的一阶近似解,当非线性项为小量时,ai和θi是缓变函数,在一个周期的量级内变化很小,求平均值时可看作常量,因此。根据两台机组转速是否相同,可以选取不同状态下的P3,R3和P1,R1,P2,R2联立,即得关于ai,θi的六元非线性方程组。当γ=1 时,可得:
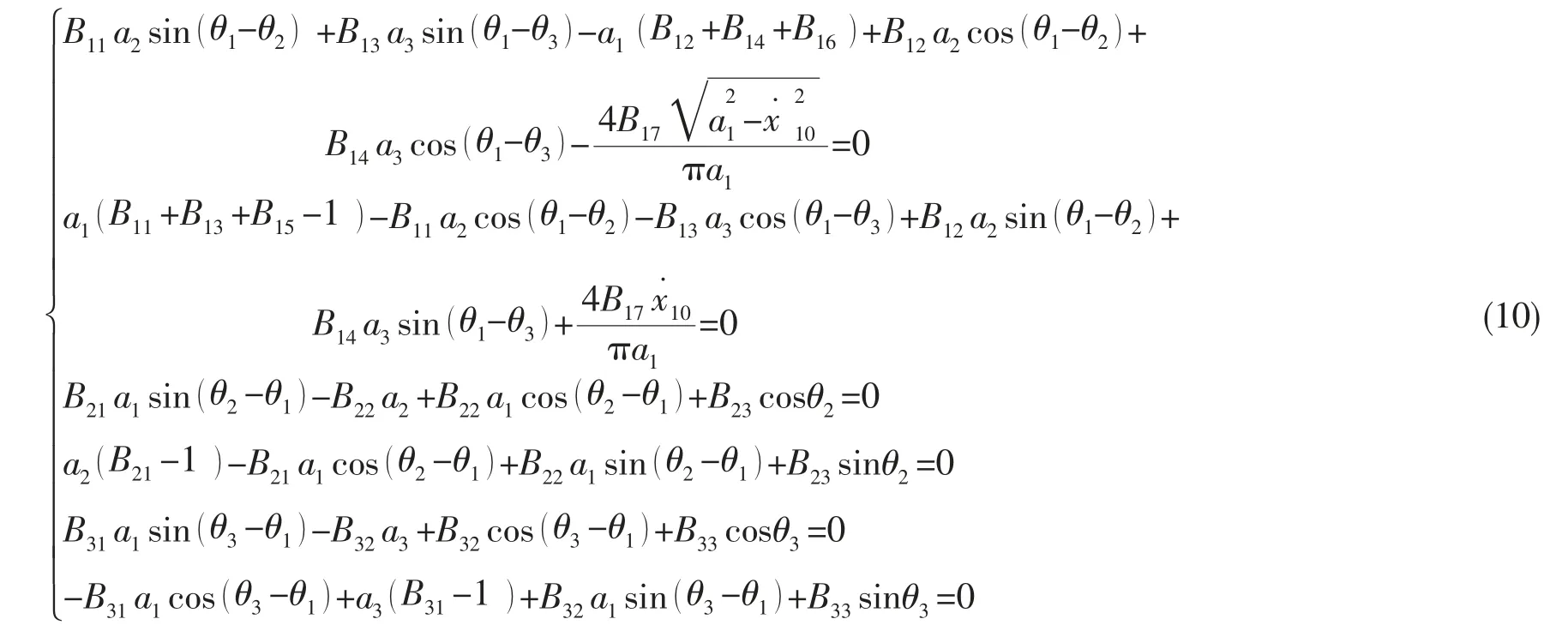
根据六元代数方程式(10),将解得的ai,θi代入(5)式,可以得到半主动浮筏隔振系统的一阶近似解析解:
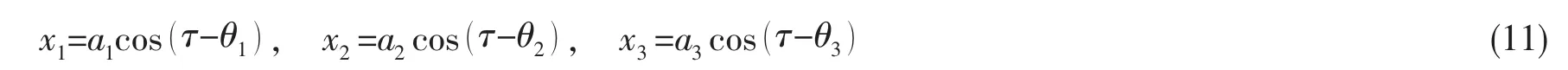
由于浮筏隔振系统同时有多个激振力作用,忽略不同机组之间激励力的相互作用,假设两台隔振机组完全相同,则此时的浮筏隔振系统的力传递率为:
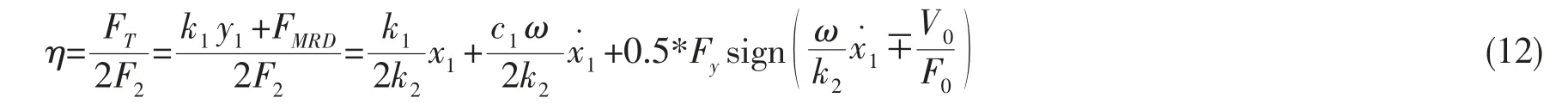
3 浮筏半主动隔振系统振动特性数值分析
为验证采用平均法得到的浮筏半主动非线性隔振系统理论解的正确性,可根据浮筏半主动非线性隔振系统的动力学方程和初始条件得到其数值解。将平均法得到的理论解与数值解进行对比,如图3所示。从图3 可以看出理论解和数值解具有很好的一致性,表明本文采用平均法得到的理论解是准确的。
动力装置与船舶基座的振动传递不仅会影响隔振系统的动力学性能,还会导致船舶产生辐射噪声,甚至损坏船上的仪器仪表设备。采用力传递率来评价隔振系统的隔振性能。根据得到的浮筏半主动隔振系统的力传递率公式(12)可以研究浮筏半主动隔振系统主要参数对隔振效果的影响规律。本文分析了磁流变阻尼器的主要参数包括阻尼系数c1,零力速度V0和控制力Fy对隔振的影响规律,其结果分别如图4-6所示。这三个参数与磁流变液的可压缩性有关。磁流变液体的可压缩性越大,阻尼越大,控制力越大,零力速度也越大。
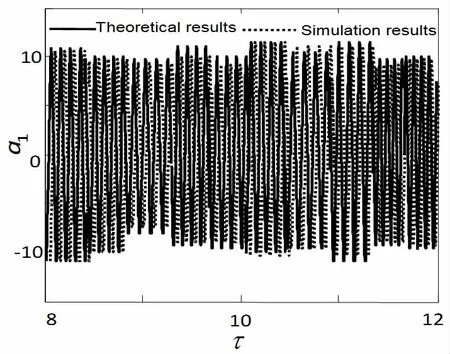
图3 浮筏半主动隔振系统响应的理论解与数值解Fig.3 Theoretical and numerical simulation solution of floating raft system
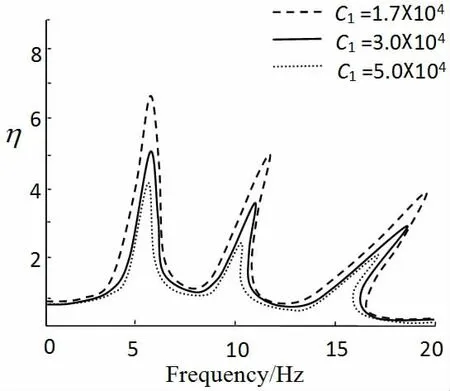
图4 c1 对力传递率的影响Fig.4 The effect of c1 on the vibration transmissibility
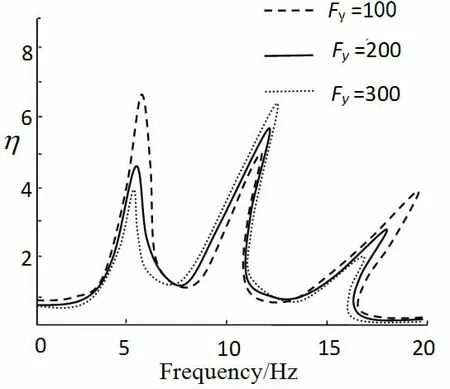
图5 Fy 对力传递率的影响Fig.5 The effect of Fy on the vibration transmissibility
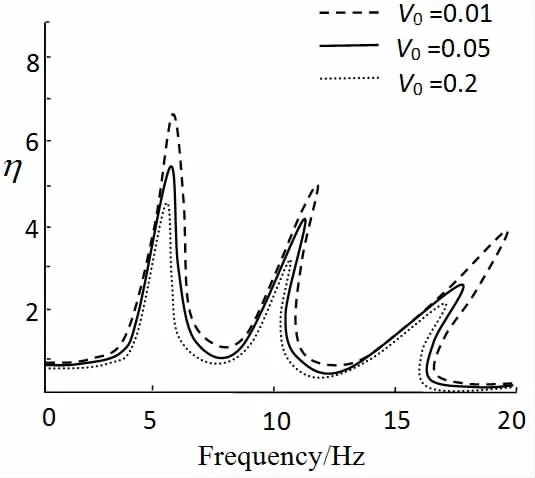
图6 V0 对力传递率的影响Fig.6 The effect of V0 on the vibration transmissibility
由图4 可以看出,浮筏系统一阶响应基本保持线性特征,二阶响应曲线和三阶响应曲线向右弯曲表现出明显的非线性特性。增加磁流变液的阻尼系数c1,可以减小系统的力传递率,从而降低传递到基座的力,其对非共振区域的减振效果影响较小,对共振区域减振效果影响明显。
由图5 可以看出,控制力Fy的变化对传递率曲线影响规律复杂。随着控制力Fy的增加,有效地降低了一、三阶力传递率,但是增加了二阶力传递率,幅值比较发现其对二阶共振影响较小;二阶响应曲线和三阶响应曲线向右弯曲主要是由控制力Fy引起的,半主动浮筏隔振系统在磁流变阻尼器控制力Fy的作用下,使非线性系统的响应表现出明显的硬刚度特性;Fy对低频响应影响较大,对高频响应影响较小,这和磁流变阻尼器的时滞特性有关。
零力速度V0对系统振动传递的影响如图6所示。随着V0的增加,各个共振区域的力传递率均减小,相对于阻尼系数c1和控制力Fy,零力速度V0对浮筏半主动隔振系统的力传递率影响较小。
从以上的力传递曲线可以看出:浮筏半主动隔振系统发生主共振时,系统的力传递率迅速增大,系统的隔振效果变差;磁流变阻尼器的各主要参数对力传递率影响规律各不相同;辅机浮筏半主动隔振系统发生共振时力传递率具有典型的非线性特性,其主要原因是磁流变阻尼器力学模型中具有典型的非线性项。
4 结论
本文为了改进船舶动力机械隔振系统的振动传递特性进而降低其辐射噪声,研究了半主动磁流变阻尼器浮筏隔振系统的隔振性能。采用改进的Bingham 模型描述磁流变液阻尼器的非线性阻尼力,该模型形式简单,参数意义明确,适合于理论研究。
通过平均法得到了半主动浮筏隔振系统响应的理论解,并通过数值结果进行了验证,结果表明得到的理论解是准确的。通过对系统力传递率特性分析,可以发现:浮筏半主动隔振系统发生主共振时,系统的力传递率迅速增大,系统的隔振效果变差;浮筏系统一阶响应基本保持线性特征,该频率附近系统的非线性特性对浮筏系统振动响应影响很弱,磁流变阻尼力主要表现为粘弹性特性,接近线性粘弹性阻尼器,因此固有频率与线性系统固有频率基本一致;浮筏系统的二阶响应曲线和三阶响应曲线向右弯曲表现出明显的非线性特征,且三阶响应曲线的非线性特性更加明显,这是因为该阶模态反映了浮筏下层的固有特性,因此其受非线性磁流变阻尼器的影响更大。改变磁流变阻尼器参数时,三阶的固有频率改变也最大。
通过磁流变阻尼系数c1、控制力Fy和零力速度V0对隔振效果的影响规律研究发现,在共振区域随着阻尼系数和零力速度的增加,可以有效降低系统各阶力传递率,从而提高系统隔振效果;控制力Fy的增加,能有效地降低一、三阶力传递率,但是增加了二阶力传递率;发生共振时阻尼系数c1和控制力Fy对力传递曲线影响较大,而零力速度V0对力传递曲线影响较小。因此,在实际工程应用中为了控制系统在低频时的主共振,可通过增加c1和Fy减小力传递率,从而减小传递到基座上的力,提高浮筏隔振系统的隔振效果。
