水面小尺度漂浮平台动力学响应分析

谢克峰，查冰婷，张 合，桂福坤，李豪杰

（1.湖北航天技术研究院设计所总体设计所，武汉430043；2.南京理工大学 智能弹药技术国防重点学科实验室，南京210094；3.浙江海洋大学 海洋科学与技术学院，浙江 舟山316000）

0 引言

水面小尺度平台是指漂浮在水面上的具有一定承载能力的小尺寸平台，能够实时动态地获取平台系统的运动信息，并根据这些信息动态地调整基座的状态[1]。水面小尺度漂浮平台[2]依靠系统浮力漂浮在水面上，属于多浮体系统范畴，通过稳定机构为负载系统提供稳定基座，抑制海浪引起的平台摆动，具有体积小、易投放的特点。为了实现小尺度漂浮平台的高精度、快速性，需对由小尺度平台形成的多浮体系统的水动力响应进行研究。

多浮体系统问题最早由Ohkusu 提出，主要针对求解波浪与多个直立圆柱的相互作用；郑艳娜、桂福坤等[3-4]对圆形重力式网箱浮架结构在波浪作用下的运动响应进行了研究，建立了浮架结构的数值仿真模型，分析了水动力系数的影响因素及在波浪下的运动响应。王冬娇[5]对浮式直立圆柱体辐射问题进行研究，采用特征函数展开等方法，分析了截断项数对计算结果的影响；李彬彬等[6]建立了时域内多立柱平台的数值预报模型，并通过模型试验考察了薄板对平台水动力性能的影响；王桂波、Fang、Kashiwagi 等[7-9]也对多浮体的运动响应特性进行了一定的研究；金振逸、李珂翔等[10-11]对海上浮动平台的受力和运动情况进行研究，分析了多体浮动平台的水动力相互作用规律。以上工作对多浮体系统研究作出了重要的贡献，然而在尺度和连接关系上，针对弹性连接件和小尺度多浮体平台尚需进一步研究。

本文基于修正的莫里森公式推导了弹性连接的主平台和浮囊的受力模型，建立了水面小尺度漂浮平台的动力学方程，通过实验对模型进行了验证，同时分析了连接件刚度和浮囊直径对主平台幅值运动响应的影响。

1 水面小尺度漂浮平台

水面小尺度漂浮平台采用立柱式方案。平台由浮囊系统（充气浮囊，弹性连接件）、主体系统（系统电源、航行电机、配重等）、稳定机构（驱动电机、支杆机构、减速器）、负载系统（探测系统，制导系统）、位姿测量系统和姿态控制与处理单元组成。平台组成示意图如图1所示。

小尺度漂浮平台的运动属于多浮体运动。小尺度平台被释放后展开浮囊系统，主平台利用浮囊系统的浮力漂浮在水面上。在海浪的作用下，主体系统和浮囊将产生一定的摇荡和垂荡运动。由于主体系统和浮囊之间为柔性连接件连接，因此两者在运动过程中会存在耦合作用，浮囊通过柔性连接件对主体系统产生一定的回复力矩，完成初级减摇稳定。主体系统通过姿态测量系统反馈倾斜角度，通过稳定机构进行调平，因此主体系统在浮囊和海浪作用下的运动响应是系统调平稳定的重要输入，运动响应特性影响了系统的调平稳定性能。

图1 水面小尺度漂浮平台结构示意图Fig.1 Structure diagram of offshore small floating platform

2 小尺度平台受力特性分析

小尺度平台受力主要包括重力、浮力、弹性力和波浪力。除重力为常量外，其余作用力均会随着时间的变化而变化。针对小尺度平台的运动特性，进行如下假设：

（1）忽略浮囊的柔性，假设为刚性体；

（2）忽略小尺度平台对流场的影响；

（3）假设波浪正向传播，小尺度平台对称布置在水域中。

基于上述假设，线性波浪条件下，小尺度平台为轴对称结构，主要包括三个自由度的运动，分别是纵移、升沉、纵倾。为便于分析，将小尺度平台的运动简化为平面的二维问题。作用在小尺度平台上的波浪力较为复杂，为了降低计算难度，进行适当的模型简化。

2.1 坐标系的建立

在研究水面小尺度漂浮平台的波浪运动响应时，将主体系统、稳定机构和负载平台简化为一个圆柱体主平台，如图2所示。建立固定坐标系O-XYZ，X 轴方向为波浪方向，Z 轴方向垂直向上，Y 轴由右手坐标系确定。分别建立与浮囊和平台固连坐标系Of-XYZ 和Op-XYZ,其中Of-XYZ 坐标系的原点Of位于浮囊中心，Op-XYZ 坐标系的原点Op位于主平台的重心。

小尺度平台受力主要分为主平台和浮囊两个构件来考虑。主平台受到浮力Ff1、重力Gp、弹性力F11和F12、分布式波浪力Fb1的作用；浮囊受到浮力Ff2、重力Gf、弹性力F11′和F12′、波浪力Fb2的作用。主平台和浮囊分别有3 个方向的自由度，即纵移x、升沉z 和纵倾θ。

图3 主平台微元波浪力作用示意图Fig.3 Wave force diagram of the host platform unit

2.2 主平台波浪力分析

小尺度平台在波浪的作用下会随波浪一起运动，主平台与波浪水质点的运动方向会产生一定的夹角，因此波浪作用在主平台上的水阻力和升力随时间在不断变化。对于倾斜圆柱体上的波浪力的计算，采用修正的莫里森公式。小尺度杆件的波浪力分析中，冲角被定义为浪向和杆件轴线的最小夹角，其范围为[0，pi/2]。结合本系统特点，将冲角定义为浪向的法向和主平台轴线的夹角。如图3所示，图中x 正方向为波浪传播方向，z 轴正方向垂直波浪传播方向向上，主平台轴线和z 轴夹角为系统的摇摆姿态角，将此角定义为上述冲角，同时定义由z 轴顺时针转动到主平台轴线为正，反之，则为负。

在分析主平台的波浪力时，将主平台离散为多个微元，分别计算每个微元上的波浪力，然后沿主平台轴线进行积分，可以得到主平台的波浪力。图3 是微元段在波浪作用下的受力示意图。微元直径为d，姿态角为θ。将波浪水质点的速度u 分解为ux和uz，加速度分解为ax和az。法向速度un和切向速度ut可以表示为：

式中：Ux和Uz分别表示微元的运动速度沿固定坐标系的分量。

单位长度微元的水阻力和升力可以表示为：

式中：An为垂直于波浪速度方向的微元的投影面积；CD1为法向水阻力系数，对于小尺寸光滑圆杆其变化幅度不大，其变化范围大约为（1.0～1.38）；CD2为切向力系数，其中CD2=Cf·CD1，对于小尺寸光滑圆杆，Cf=0.02。

由坐标转换关系，可得固定坐标系内的阻力fDx和fDz为：

主平台的长度为l0，水阻力力矩为z（t），则整个主平台的阻力矩为

同理，将加速度进行分解，根据Brebbia 关于惯性力的计算公式有：

式中：V0为微元入水体积；fMx、 fMz为x 和z 方向的惯性力分量；Ax、Az为x 和z 方向的微元的加速度分量；Cm为附加质量系数，文中由于主平台直立于水中，惯性力系数较大，取Cm为常数1.0。

主平台受到的惯性力矩为

则主平台在固定坐标系内受到的合力为Fx、Fz。

则主平台受到的完整波浪力矩为

2.3 弹性力分析

主平台通过四根弹性连接件连接到浮囊上，连接件尺寸较小，且重量轻，忽略连接件的重力、浮力、波浪力，只考虑弹性力的作用。连接件在初始状态时有一定的预拉力，作用在连接件的拉力大小与连接件的伸长量有关。连接件的伸长量可以根据连接点的坐标来计算，连接点分别位于浮囊和主平台上，通过小尺度漂浮平台的运动方程得到。

弹性作用力如图4所示。Ak1、Ak2、Ak3、Ak4分别是连接件的连接点，则弹性力可以表示为：

式中：K1为连接件的刚度，x0为连接件初始长度，弹性力与主平台轴线的夹角分别为θ1、θ2。

则作用在主平台坐标系中的弹性力为

作用在系统固定坐标系的弹性力为

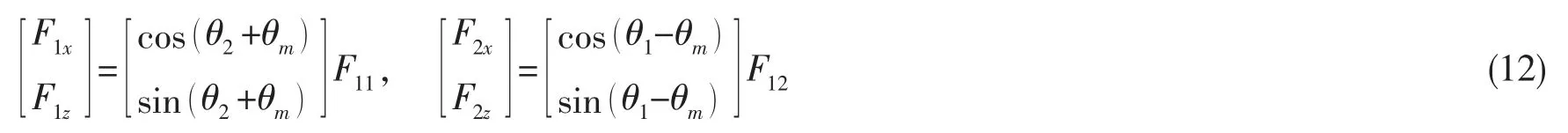
作用在主平台的力矩为

式中：xk为连接件连接点距主平台底部的距离。

以上分析为作用在主平台上的弹性力，作用在浮囊上的弹性力与作用在主平台的弹性力互为作用力与反作用力。

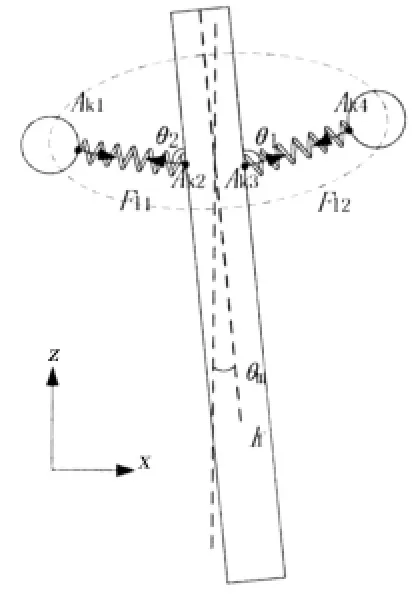
图4 连接件作用力示意图Fig.4 Force diagram of connection

图5 浮囊微元受力示意图Fig.5 Force diagram of the floating air bag unit

2.4 浮囊受力分析

小尺度平台简化到二维平面内，但是浮囊的受力分析仍需要在空间内进行，图5 是波浪作用下的浮囊状态示意图，取浮囊周长方向的微元段，定义系统坐标系xyz，x 轴方向为波浪传播方向，z 轴垂直向上；定义nτυ 为微元局部坐标系，n 为沿微元径向法线方向，τ 为沿微元径向的切线方向。其载荷主要包括波浪力、浮力和弹性力，弹性力已在前文描述。

将波浪水质点的速度和加速度沿固定坐标系x 轴和z 轴分解，假设水平速度分量ux在微元局部坐标系中的方向为｛θn，θτ，θυ｝，垂直速度分量uz的方向为｛φn，φτ，φυ｝。波浪水质点的速度在微元局部坐标系的方向由浮囊的倾角α 和微元的方向角β 决定。浮囊呈轴对称，y 方向受到的波浪力分量相互抵消。分别求得水平速度和垂直速度在局部坐标系的分量｛uxn，uxτ，uxv｝和｛uzn，uzτ，uzv｝。

由上式可以得到局部坐标系的速度分量｛un，uτ，uv｝为

则作用在浮囊微元上的波浪力可以通过Morison 公式计算。波浪条件下，修正的Morison 方程为

则作用在微段上的波浪阻力为：

式中：Ci（i= n，τ，v）为i 方向的阻力系数，Ai（i= n，τ，v）为i 方向的对应的有效投影面积。

将浮囊坐标系中的微元波浪力转换到固定坐标系中，于是有：

作用在微元上的惯性力由莫森公式知：

式中：fflx和fflz为固定坐标系x 和z 方向的惯性力分量；ax和az为波浪水质点的加速度分量；U˙x和U˙z为浮囊微元对应点的加速度分量；Cmx和Cmz为x 和z 方向的附加质量系数，si为入水横截面积。

作用于微元上的浮力为

将微段波浪力和浮力进行积分，即可得到整个浮囊受到的波浪力矩和浮力矩。

3 水面小尺度漂浮平台的动力学方程

以上分析分别求得了作用在主平台和浮囊上的力和力矩。应用牛顿第二定律，小尺度平台包括主平台和浮囊两部分，两部分之间有弹性连接件连接，在波浪的作用下，两部分的运动情况不相同，分别定义广义自由度，可得到小尺度平台在时域的运动方程：

式中：Mkj为6×6 阶的广义质量，Fk（t）为波浪场外力合力，ξ¨（t）为小尺度平台的广义加速度。k=（1，2，3）表示主平台的横荡、垂荡和纵摇，k=（4，5，6）表示浮囊的横荡、垂荡和纵摇。

上述方程解析解较难求出，采用四阶龙格库塔方法求解二阶动力学微分方程（22）即可得到小尺度平台的动态响应。

4 数值分析与试验

水面小尺度漂浮平台在波浪下的运动响应受多个因素共同影响，本文主要对关心的连接件刚度和浮囊半径进行了分析。平台分析过程中采用线性波浪理论，波高1 m，波浪频率0.785 rad/s。小尺度平台的主要参数为：主平台直径0.5 m，主平台高度7 m，平台总质量1 400 kg，吃水深度5.5 m，浮囊初始直径1.5 m。

4.1 模型验证

为了验证上述时域运动方程的正确性，在浙江海洋大学的拖曳水池进行了缩比模型试验，试验水池长度130 m，宽度6 m，深度4 m，缩比模型几何相似比尺取为1：4，按照JTJ/T234-2001《波浪模型试验规程》进行其余设置。模型布置如图6所示，在距离造波机25 m 处，漂浮系统对称布置在水池中间。试验如图7所示，姿态传感器安装在浮囊和负载系统上，数据传输线通过移动导轨与数据采集系统连接，移动导轨可以沿底座滑动，波浪方向沿导轨底座方向，浪高仪由于空间限制布置在漂浮平台的右后方。

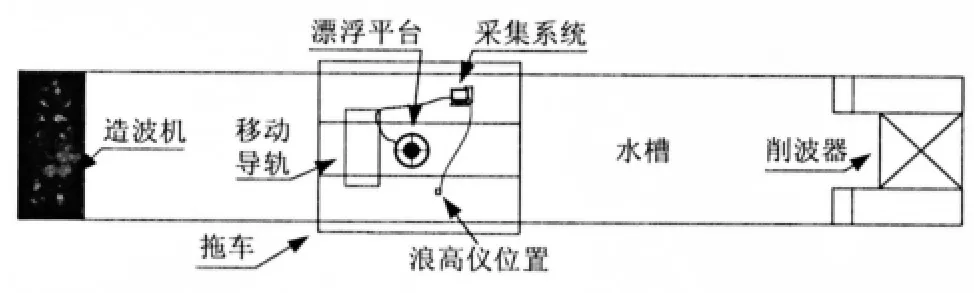
图6 模型平面布置示意图Fig.6 Sketch of the model configuration

图7 模型试验图Fig.7 Model experiment

分别对不同波高下的平台幅值响应进行数值仿真和试验，每组试验重复3 次，结果如图8所示。图8（a）给出了波高1.04 m、周期4 s 对应模型波高26 cm、周期2 s 的运动响应对比图，图8（b）给出了四组不同波高条件下幅值响应的对比图。

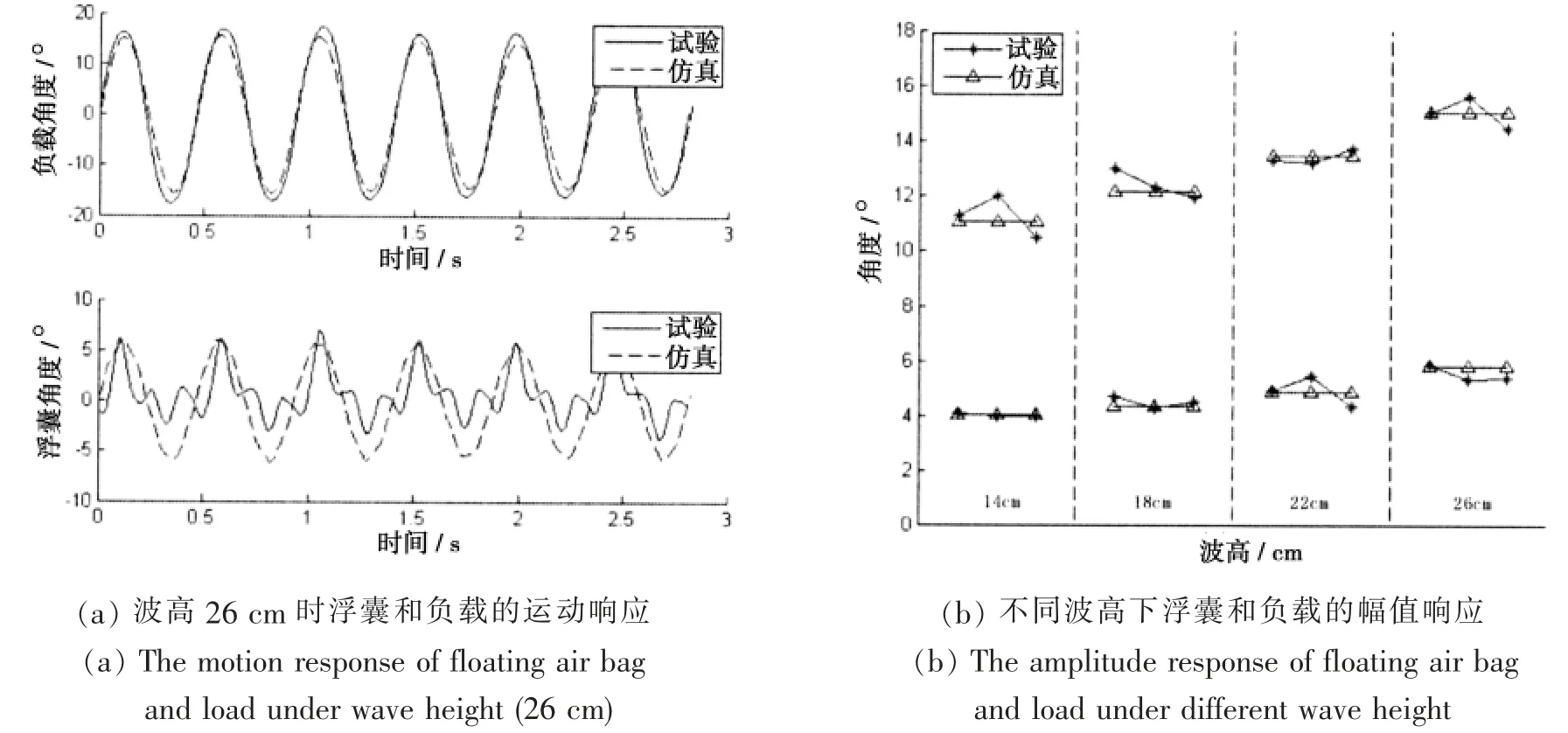
图8 不同波高下平台运动响应的仿真和试验对比图Fig.8 The comparison of motion response between the simulation and the experiment under different wave height

从图中可以看出，仿真结果与试验结果在整体上吻合较好，其中在波高为26 cm 时，负载的实际角度与仿真基本一致，而浮囊的响应曲线与仿真有一定的差别。这主要是因为在试验时，浮囊和主平台之间的四边弹性连接设置存在一定误差，同时主平台响应角度大于浮囊，对浮囊有一定的拉力作用，使浮囊响应偏向一边，而在其余情况下能够较好吻合，不同波高下，试验和仿真结果都基本吻合。这在一定程度上验证了所建立的数值模型的正确性。

4.2 连接件刚度对小尺度平台运动响应的影响

连接件分别沿x 轴和y 轴对称布置在浮囊和主平台之间，预拉伸长度为10 mm，刚度取值从5×104N/m 到500×104N/m，其中取值在拐点处较为密集，其余地方稀疏。41 次仿真结果如图9 和图10所示。图11 为连接件刚度为40×104N/m 时，浮囊和主平台的幅值响应曲线。

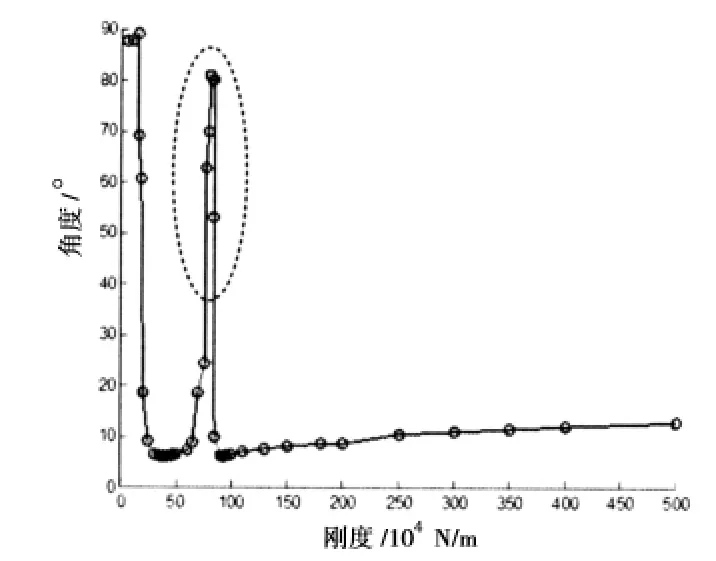
图9 幅值随刚度变化的响应曲线Fig.9 The response curve of amplitude along with stiffness

图10 频率随刚度变化的响应曲线Fig.10 The response curve of frequency along with stiffness

图9 为主平台幅值随连接件刚度变化图，从图中可以看出，连接件刚度对主平台幅值响应影响较大，主平台幅值响应随连接件刚度呈“W”变化，幅值响应最小值点分别在40×104N/m 和95×104N/m 处取得。其中连接件刚度在小于20×104N/m 时，主平台的响应幅值大于60°，最高达到了90°，此时主平台运动状态剧烈，响应幅值过大，数值结果已经不能代表真实结果，仅能显示此刻主平台的状态。

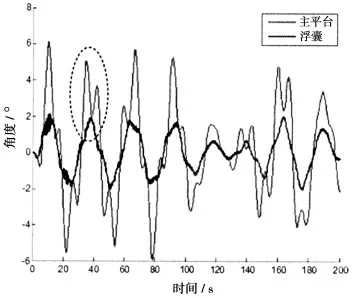
图11 最优刚度时幅值响应曲线Fig.11 The response curve of amplitude at best stiffness

主平台幅值随刚度的变化曲线主要是因为刚度太小，弹性连接件振动频率增加，在外力的作用下容易改变变形量，同时浮囊作用在主平台的回复力较弱，平台的运动响应较大；随着刚度的增加，弹性力对主平台运动的作用逐渐变大，具体表现为回复力，主平台的运动响应逐渐变小，两者的运动响应也逐渐趋于一致；刚度继续增大，弹性连接件的变形量很小，两者之间趋于固定连接，弹性力主要提供竖直向上的浮力，两者的响应频率相同，负载系统的固有频率增加，在波浪下的幅值响应有一定程度的增加。其中“W”曲线的中间凸起部分的响应频率与平台的共振频率接近，因为共振引起平台响应的急剧变化。

刚度在40×104N/m 和95×104N/m 时，均能取得最优幅值响应，但是从图10 可以看出随刚度增加，主平台的响应频率有一定的升高，高频率表示平台运动过程中抖动的增加，对平台内工作器件和高精度控制提出更高的要求，同时在30×104N/m 和65×104N/m 之间，主平台均表现稳定的幅值响应，稳定性较好，因此文中选择平台的最优刚度值为40×104N/m。40×104N/m 刚度的小尺度平台幅值响应曲线如图11所示，此时的连接件刚度适中，主平台的响应幅值大于浮囊的响应幅值，浮囊有一定程度的抖振，浮囊的回复力在主平台响应的最大幅值处表现最为明显。由于连接件作用力，主平台的幅值曲线在顶点处出现一定程度的凹下，而浮囊的幅值在此刻有明显的凸起，与实际情况一致。

4.3 浮囊直径对小尺度平台运动响应的影响

浮囊通过连接件与主平台连接到一起，不同浮囊直径，连接件的初始长度不同，保持连接件的预拉伸长度10 mm 不变，浮囊直径取值从1 m 到7 m，20 次仿真结果如图12所示。图13 为浮囊直径为2.5 m 时，浮囊和主平台的幅值响应曲线。

图12 幅值随直径变化的响应曲线Fig.12 The response curve of amplitude along with diameter

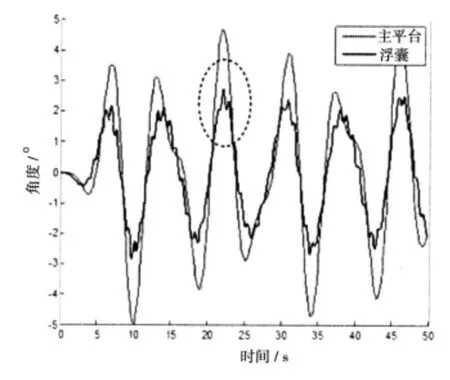
图13 最优直径时幅值响应曲线Fig.13 The response curve of amplitude at best diameter

图12所示为主平台的幅值响应随浮囊直径的变化曲线。从图中可以看出，主平台的响应幅值随浮囊直径的增大表现出变大的趋势，但是变化范围最大为51%，从最初的4.97°变化为7.52°，变化幅度较小，特别是浮囊直径从1 m 变化到3.5 m 的过程中，主平台的响应幅值最大变化范围为3.8%。因此，浮囊直径对主平台的响应幅值影响较小。

在浮囊直径变化过程中需要保持整体浮力不变，因此浮囊直径越大，浮囊越细，则连接件的初始长度越长；小尺度平台为折叠式弹开机构，在初始阶段浮囊收缩在小尺度平台内部，后经外部信号触发，打开浮囊系统，弹性连接件初始长度越长，对内部空间的要求越严格，同时，打开过程需要的时间也越长，因此，弹性连接件的长度不宜过长。弹性连接件过短对加工精度和安装要求越高，根据主平台长度为7 m，直径为0.5 m，文中选择合适的浮囊直径为2.5 m。图13 为浮囊直径2.5 m 时小尺度平台的运动响应曲线，从图中可以看出，主平台的最大响应幅值为5°，连接件作用力对主平台运动响应的影响较弱，没有明显地改变主平台的幅值响应，但是连接件作用力明显地改变了浮囊的幅值响应，在浮囊响应的最值处，受连接件作用力的影响，幅值响应出现明显的凸起。

5 结论

本文针对水面小尺度漂浮平台的特点，对小尺度平台模型进行了适当简化，简化为浮囊、弹性连接件和主平台三部分，基于修正的莫里森公式采用微元法分别推导了主平台和浮囊的受力模型，建立了水面小尺度漂浮平台的二阶动力学方程；采用四阶龙格库塔法进行数值仿真，分别对连接件刚度和浮囊直径进行了分析。仿真和试验结果表明，所建立的数值模型能够正确计算平台的运动响应；主平台的运动响应受连接件刚度影响较大，主平台随连接件刚度呈“W”变化，结合频率变化曲线，最优的连接件刚度为40×104N/m；而主平台的幅值响应受浮囊直径影响小，随浮囊直径呈微弱的增大趋势，结合结构设计特点，最优的浮囊直径为2.5 m。本文结果可为进一步研究水面小尺度漂浮平台的参数设计提供基础。