耦合激励下的液舱晃荡新型数值解法

王庆丰，徐 刚，王树齐，田 超

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江212003；2.中国船舶科学研究中心，江苏 无锡214082）

0 引言

频域理论的应用可以说已经相当成熟，但是频域法存在一个本质上的限制，即它通常只适用于周期稳态问题，对于瞬变或者强非线性问题往往无法处理。但是时域理论是频域理论的超集，是一种时间项不可分离的方法。理论上可以解决完全非线性以及物体任意运动的问题，具有相当大的自由度。本文采用基于简单格林函数的时域边界元方法，对于传统边界元方法，奇异点的处理一直是难点。本文使用的去奇异边界元法（Desingularized Boundary Integral Equation Method）将传统方法中直接布置于流体计算域表面节点上的所有奇点移至计算域外部，很好地解决了奇异积分问题。为了能够更好地模拟液舱内的运动，本文利用FORTRAN 研发了一套可以模拟任意尺度液舱晃荡的程序。

目前，基于去奇异边界元法对势流问题的研究已越来越多。Jensen 等[1]利用去奇异方法来分析在稳定入射波情况下求解阻力的问题；Cao，Schultz 和Beck[2]和Lee[3]基于时间步进技术和去奇点边界积分方程，结合二者来模拟简单潜体及浮体运动的完全非线性效应问题；李宗翰等[4]使用去奇异积分方程方法仿真了任意三维浮体的完全非线性流场；Scorpio 和Beck[5]，王大国等[6]对完全非线性数值水池进行了探索；Kara 等[7]利用去奇异边界元方法研究了完全非线性波物相互作用三维时域问题；Zhang 等[8]基于去奇异方法研究了双体船的耐波性；徐刚等[9]进行了随机波浪下三维液舱的全非线性数值分析。

1 去奇异边界元理论

1.1 控制方程及初始条件

根据势流理论，基于流体运动的连续性条件和无旋条件，速度势φ 在流体域D 中满足Laplace 方程，定解条件如下：

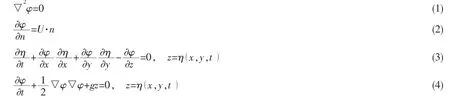
给定初始条件如下：

1.2 自由面条件差分格式

自由表面上的速度势φ 时间步进求解一般采用有限差分法。这种处理方法的缺点是相对比较复杂，而且在此过程中容易出现数值发散。本文采用一种新的积分格式的自由面条件（Integral form of free surface boundary condition[10]，IFBC）。通过此积分格式，可以由（3）式和（4）式得到自由面上一阶速度势的表达式，见（7）式。这种积分格式的自由面条件稳定性高，误差小，不会出现结果发散的现象。

对线性自由面条件采用先积分后离散的处理方法，在等式两边对t 在（0，τ1）重积分，然后再对τ1在（0，τ）中积分，可得到：

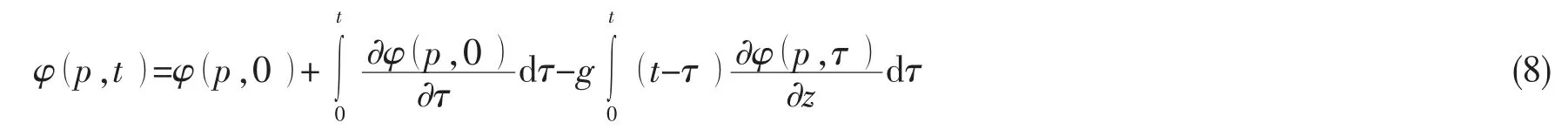
再由初始条件，上式可以写为：

然后采用如下的离散模型将（9）式进行离散：在空间上把自由面划分成若干小平面单元，并假定每个单元中心点上的物理量为常数分布；在时间上以时间Δt 为步距，等间隔前进。采用梯形公式离散（9）式，可以得到：

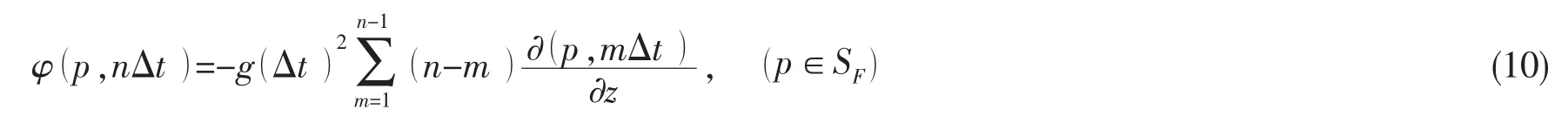
1.3 去奇异边界元积分方法

采用边界元方法的关键一步是积分方程的离散。本文基于分布源法，流场中的速度势可以表达为：

式中：p（x，y，z）为场点，即流体域内的动点；q（ξ，η，ζ）为源点，即点源所在固定点；rpq为p 和q 两点间距离，即；S1为流体域上积分表面。

因此上节提到的边界条件可改写成如下形式：

将上述二式代入（11）式，那么关于未知量σ0（q，t）的积分方程可表示为：

对于（14）式和（15）式的积分方程，传统的边界元方法都是将源强直接分布在物体及自由表面上，也就是说积分表面S1即为流域的边界。这样往往会出现由于格林函数1/rpq的分母趋于零所带来的奇异积分的问题。本文采用的方法为去奇异边界元方法，即将传统作法中原本直接布置于流体计算域表面节点上的所有奇点，移至计算域外面，也就是将传统作法中叠在一起的节点和奇点分开了。在积分边界SF和SW每个单元上分别布置强度为σF和σW的点源，SF和SW是实际流体域外距离流体域很近的积分表面，则：

将（14）-（15）式代入上式，则：

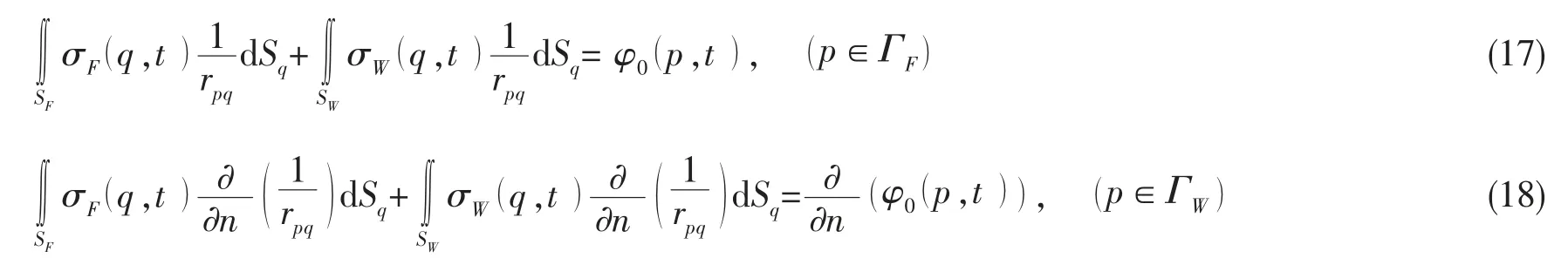
假设研究的问题中总共有N 个孤立的点源构成，则（17）式和（18）式可简化成如下的N 个孤立点源的代数和的形式：

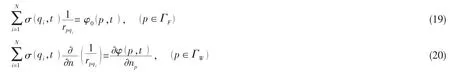
当采用上述离散方法对总共N 个配置点列写方程后，可最终得到如下N×N 的线性代数方程组：

式中：Aij为影响系数矩阵；bi为边界条件所形成的确定矩阵；σj为待求的未知源强。

求解线性代数方程组（21）后即可得出未知源强。由（10）式求得速度势，可以通过以下（22）-（24）式求得水动压力p、波高η 和水动力F。

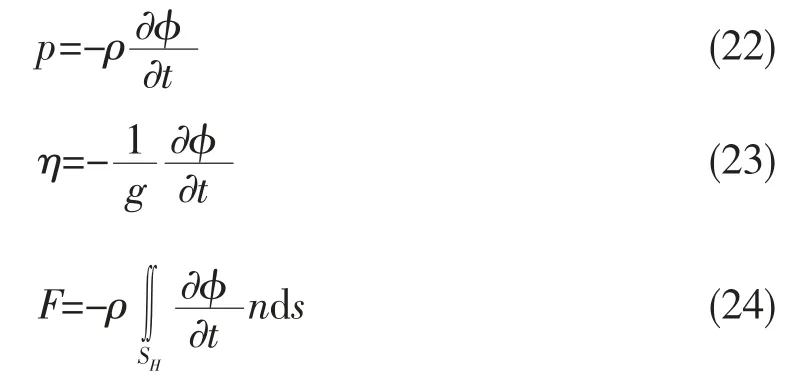
1.4 基于DBIEM 晃荡程序的流程

基于DBIEM 理论，以FORTRAN 语言为工具，本文编写了一套能够模拟任意尺寸任意形状液舱晃荡的程序。图1 是晃荡程序的基本流程图。

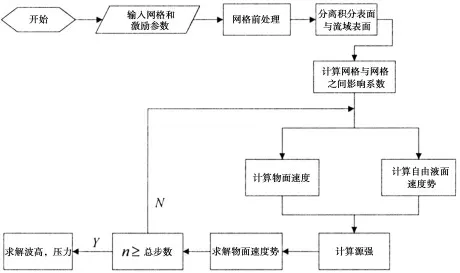
图1 晃荡程序基本流程Fig.1 The basic process of sloshing program

2 数值方法有效性验证

2.1 线性晃荡解析解

2.1.1 水平方向激励液舱晃荡

对于周期性激励ue= Acosωt，其中ue是液舱激励速度，A=bω 为速度幅值，b 为位移幅值，ω 为激励频率，Faltinsen给出了求解速度势φ 的线性解析方法，通过下式可以很容易地将求得的φ 值转化为自由液面的分布[11]（液舱水深h、长度2a、宽度2w，且原点位置在液面中心处）。

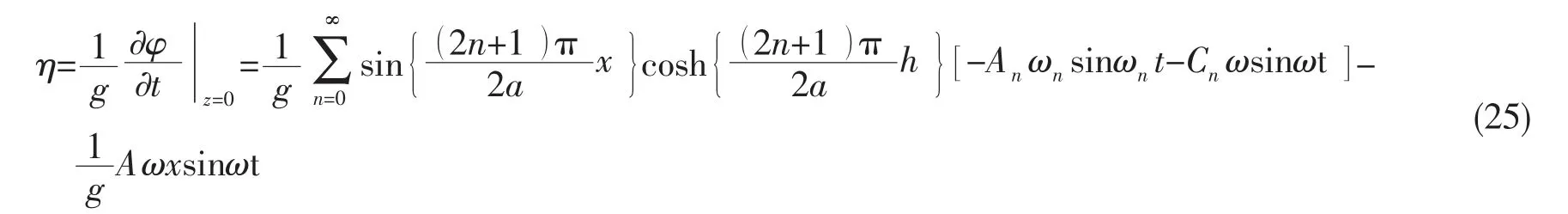
2.1.2 横荡纵荡耦合线性激励液舱晃荡

对于周期性振动ue= Acosωt，我们将振动速度ue投影到x 与y 方向并将此类问题当作横荡与纵荡耦合问题考虑。将一维线性激励下x 与y 方向的Faitinsen 解析解进行结合，即得到横荡与纵荡耦合线性激励下三维液舱液面升高解析解（液舱水深h、长度2a、宽度2w，且原点位置在液面中心处）。

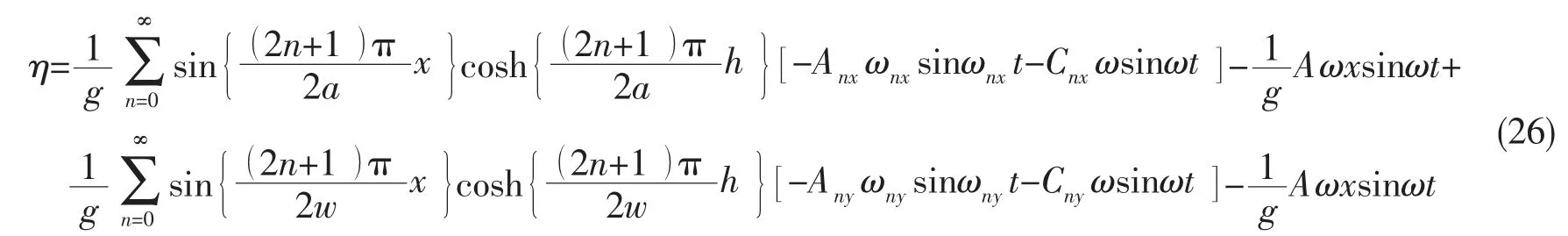
2.2 数值解与解析解对比

在数值模拟中，取坐标系O-XYZ，OXY 平面与静水面重合，Z 轴垂直向上。液舱的长和宽分别为L和B，h 表示液舱内液体高度。表1所示为液舱的主要参数。

表1 液舱主要模拟参数Tab.1 Main simulation parameters of tank

为验证程序是否准确，本文在网格收敛性分析的基础上，选取合适的网格大小、时间步长以及去奇异距离（如表2所示），模拟不同激励频率作用下液舱晃荡问题。

表2 主要计算参数Tab.2 The main calculation parameters

表2 中Nx 为液舱长度方向的划分网格个数；Ny 为液舱宽度方向的划分网格个数；Nz 为液舱高度方向的划分网格个数；dt 为时间步长；T 为激励周期；ld为去奇异距离，相当于一参数，取值范围为0～1；A 为激励幅值，单位为m。

2.2.1 单向激励下晃荡数值解法验证

考虑到微幅运动，单向激励幅值取为0.01h，h 为液舱内液面高度，入射频率分别为0.5ω0（ω0为液舱在激励方向上的固有频率，此处即为液舱的纵向固有频率），0.999 9ω0和1.1ω0。计算结果如图2所示，图中点划线为数值解，实线为解析解。

图2 不同激励频率下计算点波高时历曲线Fig.2 Time history of free surface elevation at different frequencies

从图2 可以看出，各液舱激励频率下，数值解都能够很好地与解析解吻合，误差仅在1%以内，验证了去奇异边界元法求解液舱晃荡问题的有效性。由以上各图还可以看出计算点处波高时历曲线随着激励频率的不同其变化规律也出现变化，激励频率远离液舱固有频率时如图2（a）所示，曲线变化较快，有一定规律性，波高最大值在0.006 m 左右；当激励频率接近液舱固有频率时，计算点处波峰首先随时间不断增加达到最大值后又开始下降，并以此规律不断循环，有很强的规律性，图2（c）显示了这一特征。不难看出越接近液舱固有频率波高峰值就越大，如图2（b）所示。

2.2.2 横荡纵荡耦合激励作用下液舱晃荡数值分析

针对单向微幅激励下液舱内流体运动模拟，程序已经可以达到很高的精度。当液舱受到双向耦合激励时流体运动模式会有很大的不同，程序中也要加入相应的耦合模块。因此，对于耦合激励时液舱内流体运动也要进行相应的对比分析。图3-5给出了不同耦合激励频率组合下，液舱四个角点处波高时历曲线。

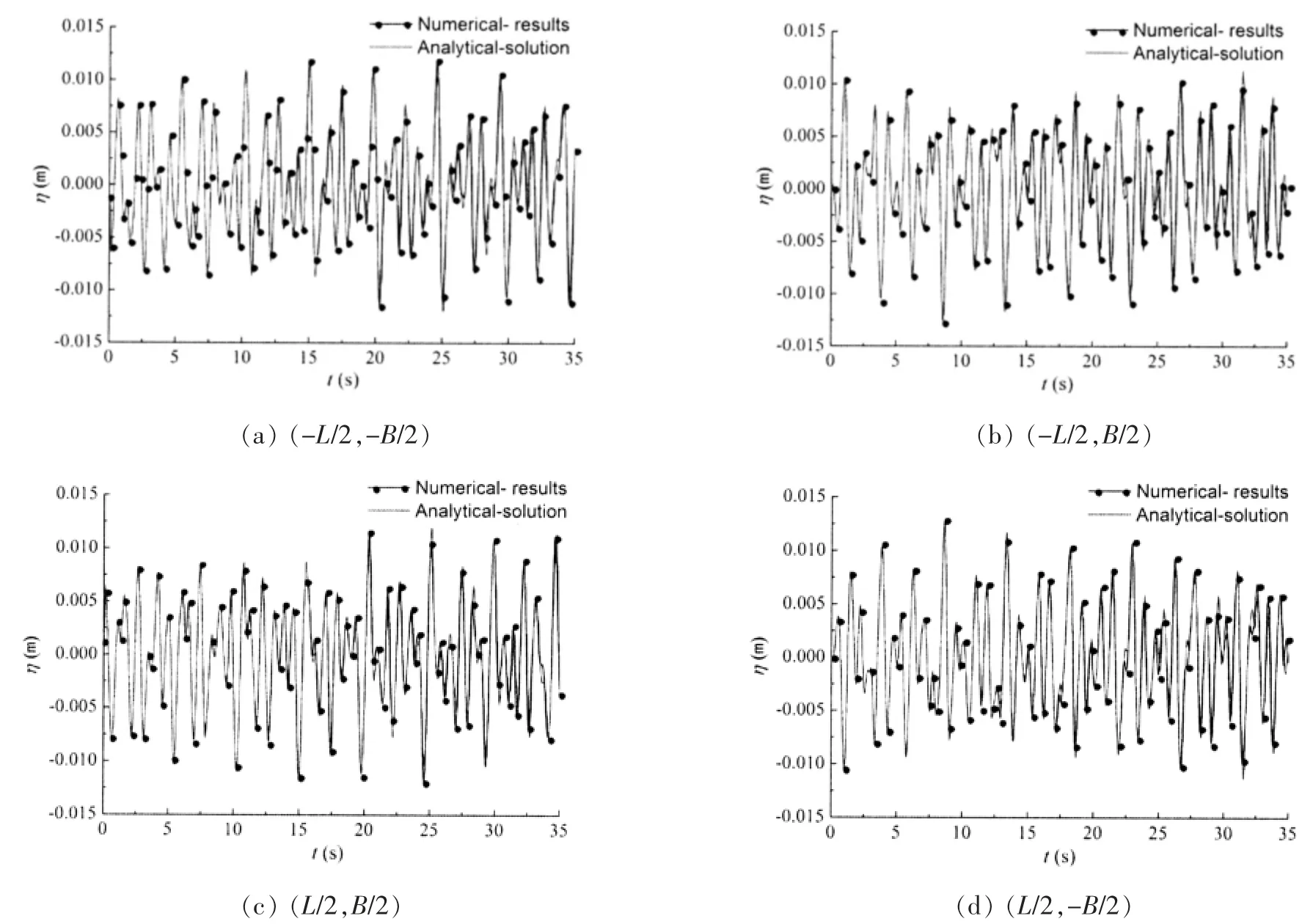
图3 ωpx=0.5ω0x，ωpy=0.5ω0y 时液面四角点的波高时历曲线Fig.3 Wave elevation history at four corners when ωpx=0.5ω0x,ωpy=0.5ω0y

图4 ωpx=0.9ω0x，ωpy=0.5ω0y 时液面四角点的波高时历曲线Fig.4 Wave elevation history at four corners when ωpx=0.9ω0x,ωpy=0.5ω0y

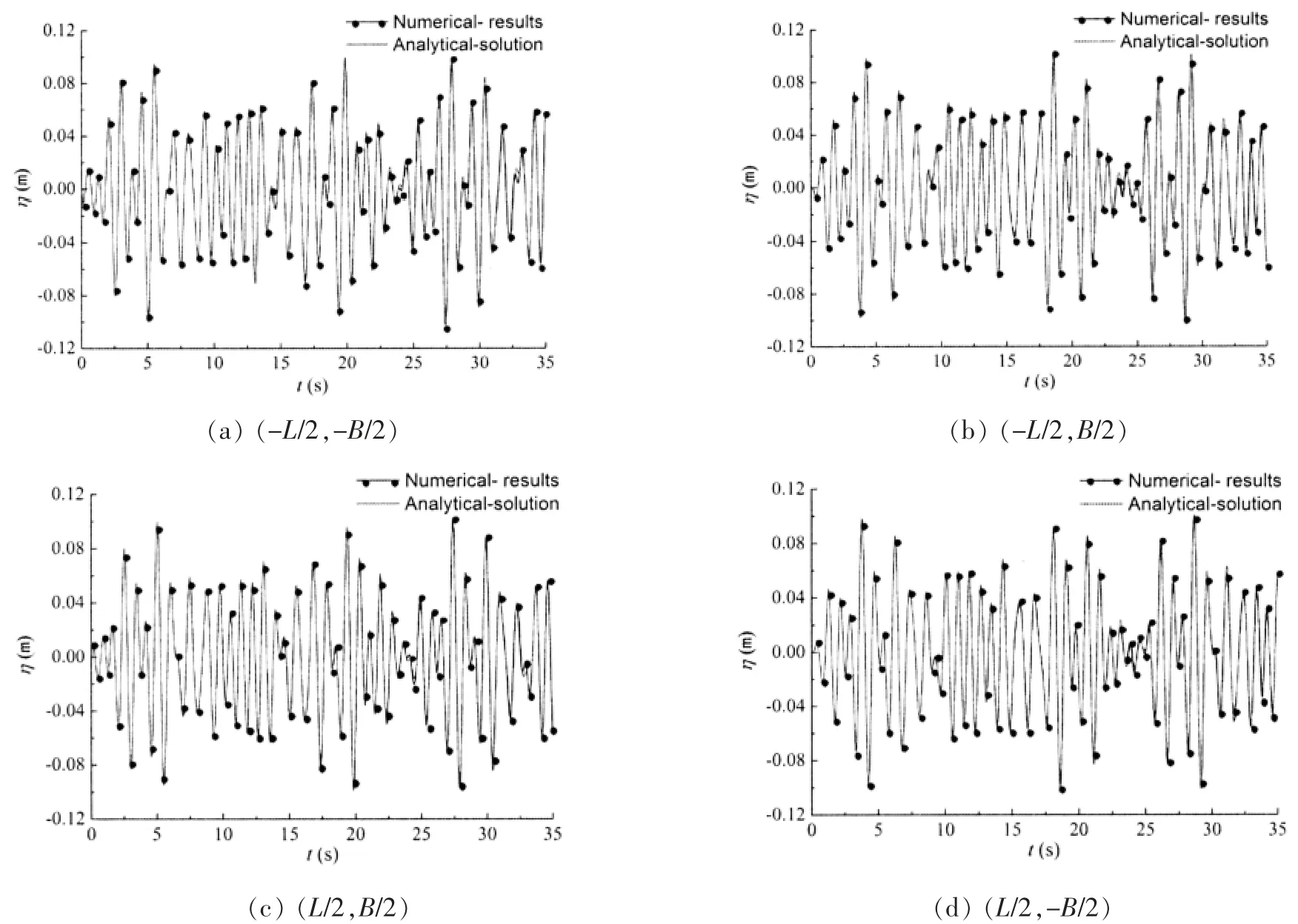
图5 ωpx=0.9ω0x，ωpy=0.9ω0y 时液面四角点的波高时历曲线Fig.5 Wave elevation history at four corners when ωpx=0.9ω0x,ωpy=0.9ω0y

图中ωpx，ωpy分别为沿x 方向与y 方向的激励频率；ω0x，ω0y分别为液舱沿x 方向与y 方向的固有频率。与单一激励相似，激励频率越接近固有频率，液舱内流体晃荡越剧烈，ωpx=0.5ω0x，ωpy=0.5ω0y时晃荡最大值约为0.013 m；ωpx=0.9ω0x，ωpy=0.9ω0y已经达到0.1 m。ωpx=0.9ω0x，ωpy=0.5ω0y时时历曲线表现出了很强的规律性，这与单一激励结果相似；但ωpx=0.9ω0x，ωpy=0.9ω0y时却比较复杂，这主要是由于当耦合激励频率接近固有频率时会产生共振并有强烈的相互干扰。

3 结 语

针对边界元方法求解波浪中结构物运动响应，尤其是在处理非线性问题时会遇到奇异性问题，本文采用了去奇异边界元方法，同时基于这一理论研发了一套可以针对不同模型不同尺寸液舱进行晃荡模拟的程序，程序中加入了六自由度运动耦合的模块，可模拟液舱在六个自由度耦合激励作用下内部液体晃荡各要素随时间变化情况，文中仅针对单一激励和横荡纵荡耦合激励下液舱晃荡问题的数值模拟，并将结果与解析解进行对比。结果表明，数值解和解析解吻合很好，验证了文中方法的有效性及对此问题的精度，可以进一步拓展到二阶或者全线性问题。