垂直激振条件下二元颗粒的能量损耗

冯玉立，赵先琼，龙 慧,2，黄达勇，刘 驰

(1.中南大学 机电工程学院，湖南 长沙 410083； 2. 韶关学院 物理与机电工程学院，广东 韶关 512005)

非阻塞性颗粒阻尼器(non obstructive particle damper, NOPD)是一种利用颗粒与颗粒、颗粒与容器壁之间碰撞和摩擦作用消耗能量的能量耗散装置[1-3]。相比于传统黏滞阻尼器、摩擦阻尼器、液压阻尼器等，NOPD具有结构简单、耐高温耐腐蚀、减振频带宽、可靠性高等优点[4-5]。Zhang等[6]研究了NOPD的流态行为和最优阻尼效果，当颗粒体系激振频率为21 Hz，振动约化加速度时有最佳阻尼效果。

二元颗粒振动系统中，颗粒体系在不同的激振条件下表现出“巴西果”(BNE)、“反巴西果”(RBN)或“三明治”(SW)等著名的尺寸分聚斑图[7-8]；何菲菲等[9]研究了铜和玻璃二元颗粒混合样品出现的SW、BNE、RBN 3种分聚结构，并测定了其相应的耗散功率； 贾敏等[10]研究了振动流化床内二元颗粒体系的分布特性，颗粒粒径比的增大、质量比的减小及振动强度的减小都有利于颗粒体系的分离，反之则利于颗粒体系的混合； 刘邱祖等[11]研究了振动特性对颗粒混合均匀性的影响，得到对颗粒混合均匀性影响最大的是频率，其次是振幅的结论；Hong等[12]对“巴西果”现象的解释，认为颗粒粒径和密度的差异使颗粒体系存在渗流与凝聚竞争机制；陈辉等[13]研究了不同体积比和密度比的二元物料的混合情况，当体积和密度满足一定配比后，渗流与凝聚作用相互竞争达到平衡状态，此时二元物料达到均匀混合状态。

目前，对二元颗粒体系在混合状态下的流动形态和能量耗散行为的研究鲜有报道，离散元方法能够描述每个颗粒在任意时刻受力与运动情况，但是由于颗粒体系的高度非线性及影响因素的复杂性，简化的理论计算模型与实验结果有相当大的出入[14]，本文中基于Hong的渗流与凝聚竞争理论，设计悬臂梁振动试验，对比一元钢球，分别从分层和混合状态分析了二元颗粒体系的能量耗散水平。

1 实验

实验装置如图1所示，颗粒阻尼器由质地较硬且透明的亚克力材质制作而成，直径为50 mm，高为120 mm，底部固连法兰盘，通过螺栓固连在悬臂梁上，悬臂梁由铝合金制成，长为332 mm，宽为58 mm，厚为3.5 mm，由功率放大器采用正弦信号激振，激振器传递给悬臂梁的力由拉压力传感器采集，激振点处的加速度信号由加速度传感器采集，信号采集仪将力信号和加速度信号传递给计算机进行信号分析处理，采样频率为10 kHz。

图1 测量颗粒阻尼器能耗的实验装置Fig.1 Experimental unit of measuring energy consumption of particle damper

悬臂梁颗粒阻尼系统主要有颗粒阻尼和悬臂梁自身的材料内阻尼损耗能量。由振动力学知，在稳态有阻尼受迫振动系统中，阻尼消耗的能量等价于激振力所做功，对于稳态振动，激振器输入功率即为系统损耗功率，因此，颗粒阻尼器损耗功率即为颗粒阻尼系统损耗功率与对应振动状态下未装填阻尼颗粒时悬臂梁系统损耗功率之差

(1)

式中:F、v分别为装填阻尼颗粒时激振器作用在悬臂梁上的力和激振点处速度大小;Fbeam、vbeam分别为未装填阻尼颗粒时激振器作用在悬臂梁上的力和激振点处速度大小。

内部损耗因子表征系统在一个周期内损耗的能量占系统最大能量的比值，可由下式[15]得到:

(2)

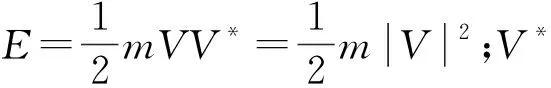
2 结果分析

垂直振动条件下，初始为分层状态的二元颗粒，当激振强度较小时，2种颗粒保持分层状态； 初始为混合状态的二元颗粒，当激振强度较小时，2种颗粒活动性较差，没有明显的分层现象产生，当激振强度增大时，颗粒的活动性增强，大颗粒间的间距变大，小颗粒有从大颗粒间隙向下层运动趋势； 当激振强度足够大时，小颗粒又有从大颗粒间隙向上层运动的趋势，实验观察到的现象与Breu等[16]的描述一致。

二元颗粒分层状态能耗试验中激振强度均未达到使二元颗粒混合的强度，混合状态能耗试验中激振强度保持在二元颗粒未发生明显分层状态的水平。

2.1 二元颗粒分层状态能耗分析

2.1.1 不同粒径对颗粒体系能耗的影响

选用直径为3 mm的钢球作为第1颗粒，第2颗粒为直径为3～10 mm钢球，2种颗粒质量各取0.15 kg，当第2颗粒为3 mm钢球时，颗粒体系为一元颗粒。激振频率为25 Hz时，不同振幅下，颗粒体系能耗随第2颗粒粒径变化如图2所示。

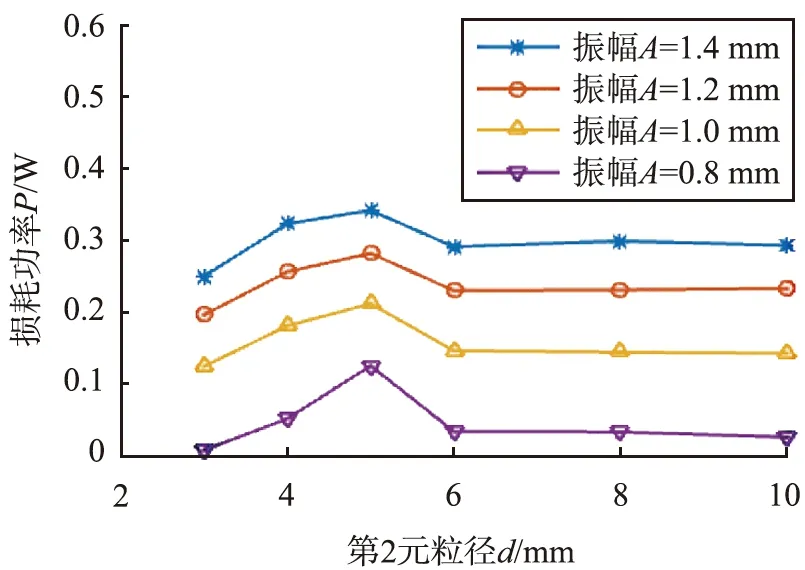
图2 颗粒能耗随第2颗粒粒径变化Fig.2 Energy loss of particles varies with size of other particles

整体上不同粒径比的二元颗粒相对一元颗粒(第2颗粒粒径为3 mm)有更大的能量损耗，随着第2颗粒粒径的增大，颗粒体系能耗先增大后减小，最后处于稳定水平，第2颗粒粒径为5 mm时有最优能耗，并且能耗随振幅增加而增大，增长速率逐渐变缓。

颗粒阻尼主要由颗粒间的碰撞和摩擦发挥能量耗散作用，当激振强度较大时，颗粒活动性增强，能量损耗以颗粒的碰撞为主[17]。2个颗粒对心碰撞损耗的能量[18]为

(3)

式中：m1、m2分别为2个颗粒质量；vr0为2个颗粒碰撞前相对速度大小；e为2个颗粒之间的碰撞恢复系数。

增大颗粒质量可以提高碰撞强度，有利于增大能耗，由此二元颗粒能量耗散水平相对一元颗粒有明显提高，但在质量一定的情况下，增大单个颗粒的质量必然减少颗粒数量，相同激振条件下颗粒的碰撞频率就会降低，因此不宜过分追求碰撞强度的提高，而忽视颗粒数量减少引发的碰撞频率的降低。

2.1.2 不同分层状态二元颗粒能耗分析

选用直径均为5 mm，质量均为0.18 kg，材质分别为玻璃和钢的二元颗粒进行分层试验，激振频率为25 Hz，能量损耗水平随振幅变化如图3所示，对照组为0.36 kg的5 mm钢球。

玻璃球居底层二元颗粒体系能耗整体优于钢球居底层能耗，这是由于单个玻璃球质量小于钢球，当振幅增大后，颗粒体系能耗以碰撞为主，惯性较小的玻璃球在上层钢球和下层悬臂梁底板之间更容易来回碰撞，提高了悬臂梁向颗粒体系输入功率，直接导致颗粒体系能量增加，颗粒活动性增强，能耗水平也随之提高。

图3 二元颗粒能耗随振幅变化Fig.3 Energy loss of binary particles varies with amplitude

相同粒径的一元钢球在振幅小于1.7 mm时，能耗水平小于钢球居底的二元颗粒，振幅大于1.7 mm时能耗有大于钢球居底的二元颗粒的趋势。

另外，玻璃球居底层二元颗粒体系能耗随振幅变化曲线与相同粒径的一元钢球能耗曲线变化趋势一致，到达相同能耗前者所需振幅比后者小0.18 mm左右。

2.1.3 质量比对颗粒体系能耗的影响

选用直径均为3 mm的钢球和玻璃球作为二元颗粒，总质量为0.2 kg，钢球居于底层，玻璃球质量比在0.25～0.75之间，激振频率为25 Hz，能量损耗随玻璃球质量比变化如图4所示。

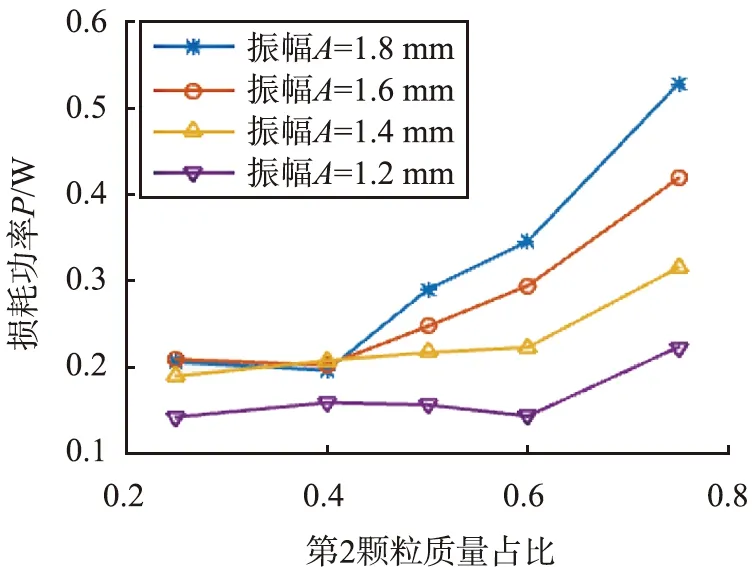
图4 二元颗粒能耗随质量比变化Fig.4 Energy loss of binary particles varies with mass ratio

整体上，颗粒能耗随玻璃球质量比的增加而增大，当玻璃球质量比大于0.4时，颗粒能耗随振幅的增加快速提高，且在颗粒能耗增大速率随振幅的增加而增大。

玻璃密度远小于钢，阻尼器内部颗粒总数随玻璃球质量比提高而增大，在相同的激振条件下，玻璃球质量比高的颗粒间碰撞频率远大于玻璃球质量比较低的颗粒体系，并且碰撞频率增大的能耗增加作用大于碰撞强度降低导致的能耗减小作用，整体上颗粒能耗处于增大趋势。玻璃球质量比小于0.4，振幅大于1.2 mm时颗粒能耗随振幅增大无明显变化，可能是由于颗粒运动的随机性带来的系统的非线现象导致，具体原因需进一步研究。

2.2 满足体积和密度配比时，二元混合颗粒能耗分析

2.2.1 混合程度对颗粒体系能耗的影响

试验发现，当大钢球和小玻璃球满足密度比为3.0，体积比为8.0时，二元颗粒体系可以处于稳定的混合状态这种现象可以用Hong等[12]的渗透与凝聚机理解释，当小颗粒向下层运动的渗透作用和大颗粒向下层运动的凝聚作用相互平衡时，不会出现分层现象。

选用直径分别为3 mm的玻璃球和6 mm的钢球，表观体积均为30 cm3，玻璃球和钢球的密度实际测量值分别为2 673、8 021 kg/m3，满足颗粒体积和密度配比，初始下料方式为小玻璃球居底层、大钢球处于上层，保持激振频率为25 Hz，振幅为2.0 mm的激振作用下，初始分层的二元颗粒体系逐渐趋于混合，最终达到稳定的均匀混合状态，混合程度随时间变化如图5所示，能量损耗随时间的变化如图6所示。

二元颗粒体系在振动条件下逐步混合，最后达到稳定的均匀混合状态，然而颗粒体系的功率损耗却恒定不变，由此可以认为二元颗粒的混合程度对颗粒体系的能量损耗没有影响，下文将不考虑混合程度对颗粒体系能耗的影响。

图5 混合程度随时间变化Fig.5 Mixing degree varies with time

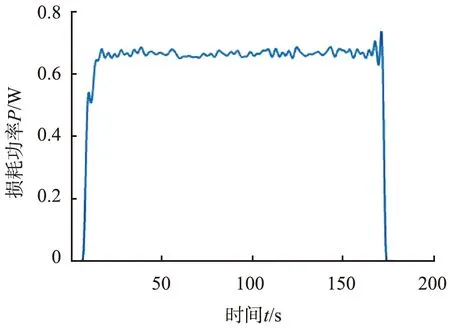
图6 颗粒能耗随时间变化Fig.6 Energy loss varies with time

2.2.2 振幅对二元混合颗粒体系能耗的影响

将上述满足质量和密度配比的小玻璃球和大钢球混合之后，在激振频率为25 Hz的条件下，二元颗粒体系能耗随振幅的变化情况如图7所示，总质量相同的6 mm钢球为对照组。

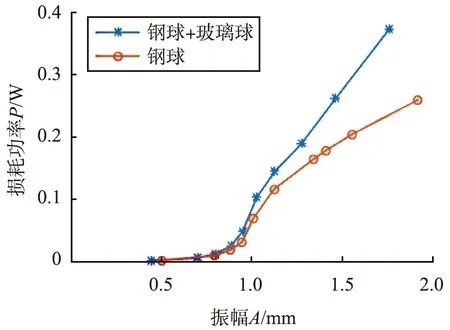
图7 能量损耗随振幅变化Fig.7 Energy loss varies with amplitude

当振幅小于0.4 mm时，颗粒在竖直方向上最大加速度小于重力加速g，颗粒与悬臂梁保持接触，颗粒间未发生相对运动，此时颗粒体系处于类固态，未发生能量耗散；当振幅大于0.4 mm后颗粒开始流动，颗粒相对运动引发能量耗散作用，能耗随着振幅的增加而增大。在振幅为0.85 mm时，二元混合颗粒和一元钢球能耗发生第1次突变，增长率突然变大，振幅在1.1 mm左右，二元混合颗粒和一元钢球体系发生第2次能耗突变点，2次能耗突变点对应2次损耗因子突变点，如图8所示，第1次损耗因子突变点之后，二元混合颗粒和一元钢球的损耗因子都急剧增大，值得注意的是，第2次损耗因子突变点之后，一元钢球的损耗因子趋于平缓，并稳定在0.21附近，而二元混合钢球损耗因子持续增大，二元混合颗粒体系在大振幅激振条件下表现出优异的能量耗散能力。

2.2.3 频率对二元混合颗粒体系能耗的影响

将上述满足质量和密度配比的小玻璃球和大钢球混合之后，在约化加速度Γ(=A(2πf)2/g)为3.3的条件下，二元颗粒体系能耗随频率的变化如图9所示。

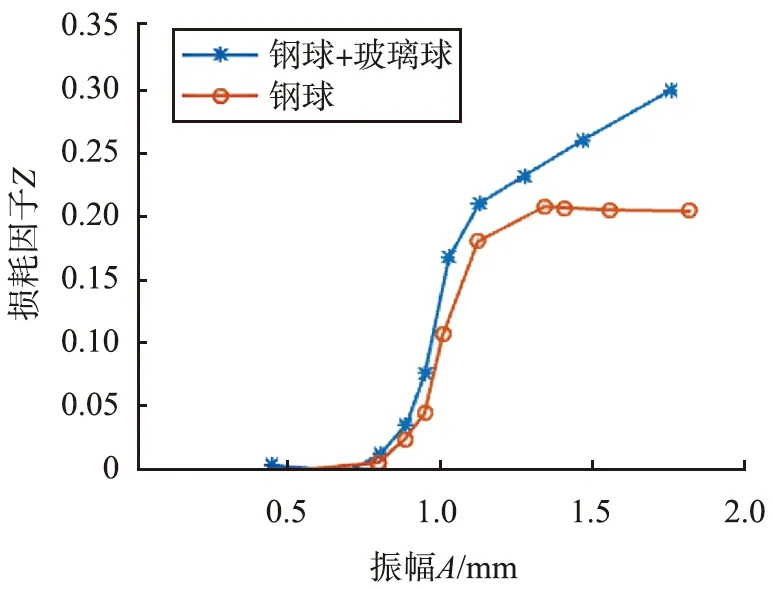
图8 损耗因子随振幅变化Fig.8 Loss factor varies with amplitude

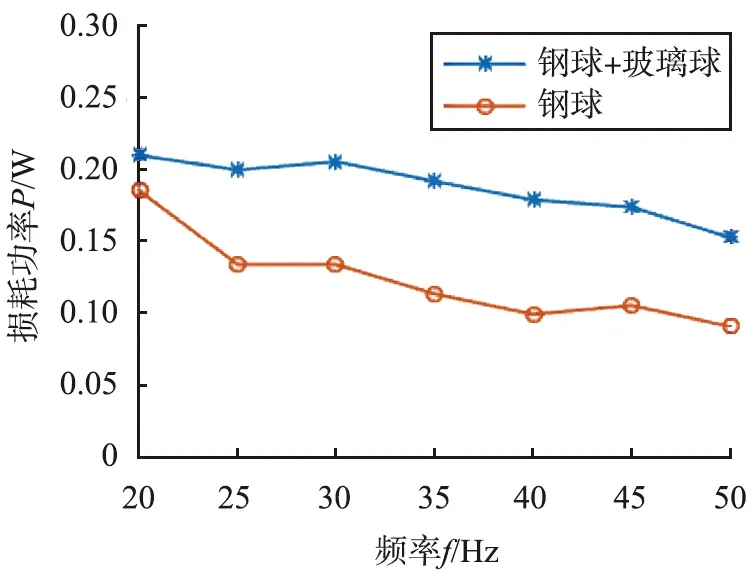
图9 能耗损耗随频率变化Fig.9 Energy loss varies with frequency

在约化加速度Γ一定的情况下，二元混合颗粒和一元钢球的能耗均随频率的提高而降低，这是因为振幅随频率提高而快速减小，振幅的变化颗粒体系活动性起主要作用，因而颗粒体系能耗随活动性增强而减小。

二元混合颗粒能耗在不同频率下均大于一元钢球，对比张凯[6]在研究一元颗粒时，得出在激振强度，Γ=3.3,f=21 Hz时颗粒发挥最优阻尼的结论，二元颗粒体系相对一元钢球的确有更优异的能量耗散能力，并且在高频激振下，有更显著的能耗提升效果。

2.2.4 质量比对二元混合颗粒体系能耗的影响

选用满足质量和密度配比的3 mm玻璃球和6 m的钢球，总质量保持在0.36 kg，将玻璃球作为第2颗粒，其质量比在0.08～0.33之间，激振频率为25 Hz，二元颗粒体系混合之后能耗随第2颗粒质量比变化如图10所示，质量比为0表示不含玻璃球。

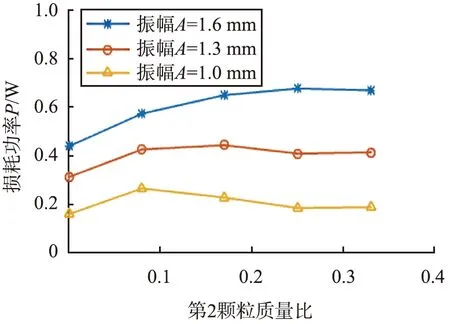
图10 二元混合颗粒能耗随质量比变化Fig.10 Energy loss of binary mixed particles varies with mass ratio

含有玻璃球的二元混合颗粒体系在不同振幅下能耗均高于相同质量钢球，在大振幅下有更明显的能耗提升效果；在相同振幅激振下，不同质量比的二元混合颗粒具有不同能量耗散效果，振幅为1.0 mm时，玻璃球质量比为0.08时有最优能耗，振幅为1.3 mm时，最优能耗对应的玻璃球质量比提高至0.17，振幅为1.6 mm时，玻璃球质量比为0.25时对应最高能耗。

二元混合颗粒体系中，对应最优能耗的玻璃球质量比随振幅的提高而增大，较大激振条件下颗粒活动性增强，大钢球之间活动间隙变大，适当的小玻璃球填充才能取得最优能耗。

3 结论

1)二元颗粒体系不论在分层状态或者是混合状态时，相同激振条件下能耗损耗均大于相同质量的一元颗粒。

2)二元颗粒处于分层状态时，相同材质的2种颗粒粒径并非相差越大越好，粒径为5 mm颗粒与粒径为3 mm颗粒组合将取得更优的能耗效果；相同大小的二元颗粒，质量较小的颗粒居于下层能够取得更高的能耗水平；总质量相同的钢球和玻璃球，颗粒能耗随玻璃球质量比增大而提高，且在较大振幅下有更显著的能耗提升效果。

3)当大钢球和小玻璃球满足密度比为3.0，体积比为8.0时，二元颗粒体系可以处于稳定的混合状态，颗粒体系的能耗与2种颗粒混合程度无关；在不同振动幅值、频率和不同质量比的情况下，二元混合颗粒体系能量损耗均大于一元颗粒；颗粒体系的玻璃球最优质量比随振幅的提高而增大。

综上，二元颗粒体系能耗增加是因为第二颗粒的引入增加了颗粒体系内部的不均匀性，加剧了颗粒体系的碰撞和摩擦作用，相对于传统的一元颗粒阻尼器有更优异的能量耗散水平，提高了颗粒阻尼器的振动抑制效果，具有显著的工程应用价值。