Numerical Analysis on Thermal Function of Clothing with PCM Microcapsules

LIU Wenyi,LI Fengzhi,LIU Weihua*

1.Nanjing Engineering Institute of Aircraft Systems,Nanjing 210000,P.R.China；2.College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China

Abstract: To study the influences of phase change material（PCM）microcapsules in clothing on human thermal responses,a mathematical model is developed. The improved Stolwijk’s model is used to simulate human thermoregulatory process,and the coupled heat and moisture transfer including the moisture sorption /desorption of fibers and effects of phase transition temperature range on the phase change processes of the PCM is considered in clothing model. Meanwhile,the theoretical predictions are validated by experimental data. Then,the interactions between human body thermal responses and the heat and moisture transfer in clothing are discussed by comparing the prediction results with PCMs and without PCMs. Also the effects of fiber hygroscopicity on clothing and human thermal responses are compared. The conclusion shows that the clothing with PCMs microcapsules can delay the human temperature variations and decrease the sweat accumulation rate on the skin surface and heat loss during changing of ambient conditions,and fiber hygroscopicity reduces the effect of PCM microcapsules on delaying garment temperature variations very significantly.

Key wor ds: PCM microcapsule; porous textiles; heat and moisture transfer; numerical simulation; human thermoregulatory model

0 Introduction

In recent years,functional textiles have been developed to enhance textile performances according to consumers’demands. One of the possible ways to manufacture functional or intelligent textile products is the incorporation of microcapsules or the use of microencapsulation processes for textile finishing. To improve thermal comfort of the wearer,phase change material（PCM）microcapsules have been applied to manufacture thermoregulatory textiles. The phase change materials possess the ability to absorb or release heat while changing their state within a certain temperature range［1］.With this characteristic,PCMs are entrapped in a microcapsule of a few micrometers in diameter to protect them and to prevent their leakage during its liquid phase. In 1980s,NASA applied PCM microcapsules technology to fiber or textile to develop the space suit featuring good thermal-regulatory function［2］.

There were many researches on manufacturing textiles with PCM microcapsules and investigating the properties of clothing with PCM microcapsules.In 1995,Pause［3］investigated the development of heat and cold insulating membrane structures with phase change materials. In his investigation,tests were carried out to develop a new membrane material with improved thermal properties. In 1999,Bryant［4］introduced melt-spun fibers containing microencapsulated phase change material. Shim［5］investigated the effects of a PCM on heat and moisture transfer in clothing. They found that the magnitude of the heat loss depends on the number of PCM garment layers,the orientation of the PCM layer to the body,and the amount of body surface area covered by the PCM garments. However,the above studies were entirely experimental,and not backed up by theoretical analysis and simulation. Nuckols［6］established an analytical model of a diver’s dry suit enhanced with microencapsulated phase change materials. Hittle and Andre［7］used a mathematical model to study the influence of PCM on a dry fabric. However,most of the textile fibers are hygroscopic,and this influences thermal comfort significantly. Considering the interaction between the fiber hygroscopicity and phase change of PCM,Li and Zhu［8］developed a mathematical model,in which the phase change process was considered as a moving boundary problem,and the phase change temperature was considered as a point. The PCMs applied in clothing are not pure substances,but mixtures of the paraffin,and the phase change takes place within a temperature in a certain range which is related to heating/cooling rate. From the analysis on phase diagram,He et al.［9］showed that all mixtures would melt and freeze in a temperature range but not at a constant temperature,except for the minimummelting point mixture. In order to consider the effect of the temperature range of the phase change,a new model was developed in Ref.［10］based on Ref.［8］,and the influences of the fiber hygroscopicity on delaying clothing temperature variations of the PCM were discussed.

In order to study the influence of clothing with PCM microcapsules on human thermal responses,this paper develops a new model of heat and moisture transfer in human-clothing with PCM microcapsules-environment system based on Ref.［10］and the improved Stolwijk’s human thermo-regulatory model［11］. Based on the model,influences of the fiber hygroscopicity on clothing with the PCM and human body thermal responses are studied.

1 Mathematical Model

1.1 Improved Stolwijk’s model

In the Stolwijk’s model［11］,human body consisting of a controlled system and a controlling system is considered. The controlled system is associated with geometric characteristics,fundamental thermal characteristics and energy transfer physical mechanisms,whereas the controlling system regulates body temperature through sweating,shivering and variable blood flow rate.

The controlled system of the Stolwijk’s model consists of cylinders of different sizes representing trunk,arms,hands,legs and feet,and the head is represented as a sphere. The cylinders or segments are subdivided into four concentric layers representing the core,muscle,fat,and skin layers. An additional central blood pool representing the large arteries and veins,exchanges heat with all other compartments via the convective heat transfer occurring with the blood flow to each layer. The heat balance equations for each layer and blood can be written as follows.

where i denotes the segment,j the tissue layer,C the thermal capacity,T the temperature,t the time,Q the metabolic rate,B the heat loss by blood flow,D（i,j）the heat flow from i-th segment’s j-th layer by thermal conduction,RES the respiration heat loss,Qtthe heat loss by thermal radiation and convection,and E the heat loss by evaporation through the skin surface. Subscript b denotes the blood.

The calculation method of evaporation heat loss from skin surface of the i th segment to environment is improved by using Jones’method［12］

where Pskdenotes the water vapor pressure on skin surface,which can be calculated by using Jones’method. Peais the ambient vapor pressure,Reathe evaporation thermal resistance of water vapor,and S the skin area.

When there is no accumulation of moisture on skin surface［12］,we have

where mrswis the regulatory sweating rate,Reskthe evaporation resistance of skin,and hfgthe vaporization heat for sweat.

When there is moisture accumulation on skin surface,we have

The liquid sweat accumulation on skin surface of the i th segment can be described by［12］

where msis the mass of sweat accumulation.

The dry heat loss from skin surface to the clothing can be calculated by the following formulation

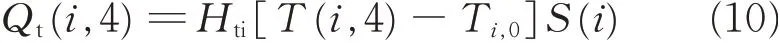
The heat transfer coefficient of an air layer is given by Hti=hr+ka/tai,where taiis the thickness of air layer,hrthe radiation heat transfer coefficient,and kathe heat conductivity of air. The values of hrand kawere optimized in the previous study which resulted in hr= 4.9 W/（m2·oC）and ka=24 mmW/（m2·oC）［13］. Ti,0is the temperature at inner surface of the clothing near the i-th segment.

In the Stolwijk’s model［11］,the error signal Err（i,j）is calculated by the set-point temperature Tset（i,j）,which plays a role of“control target temperature”,shown as

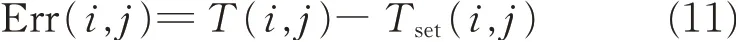
Warm signal Wrm（i,j）and cold signal Cld（i,j）,corresponding to warm and cold receptors,respectively,are defined by Eq.（12）when Err（i,j）＞0 and Eq.（13）when Err（i,j）＜0.

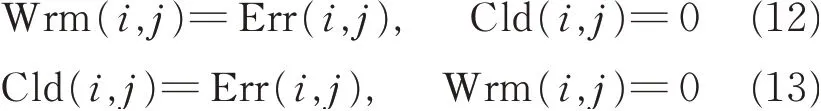
Integrated sensor signals from skin thermo-receptors are used as the control variables. Integrated warm signal（Wrms,°C）and integrated cold signal（Clds,°C）are defined by Eqs.（14）—（15）.SKINR（i）is the weighting coefficient for integration.

All control equations are composed of three terms.One is related to the head core signal,the other is related to the skin signal,and the third term is related to both. The thermoregulatory system consists of four control processes：Vasodilation,vasoconstriction,perspiration and shivering heat production.

Skin blood flow BF（i,4） is calculated by Eq.（16）. DLand STare the signals for vasodilation（Eq.（17））and vasoconstriction（Eq.（18））.

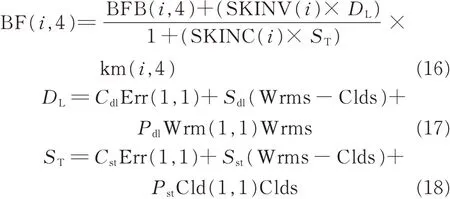
where SKINV（i）and SKINC（i）are the weight coefficients for vasodilation and vasoconstriction. km（i,4）is called the“local multiplier”,a factor for incorporating the effect of local skin temperature on vasomotion and perspiration,defined by Eq.（19）.In this paper,value of RT（i,4）is considered to be 4 °C for all segments.

The sweat generation rate of sweat mrsw（i）is calculated by Eq.（20）

where SKINS（i）is the weighting coefficient for sweat.

The shivering heat production Ch（i,2）is calculated by

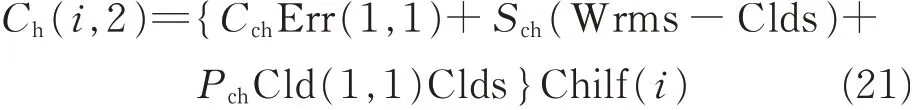
where Chilf（i）is the distribution coefficient of individual muscle layer for the shivering heat production. Other detailed information can be found in Ref.［11］.

1.2 Heat and moisture tr ansfer model for clothing with PCMs micr ocapsules

Here,the equations of heat and moisture transfer in clothing with PCMs microcapsules developed in Ref.［10］are used.

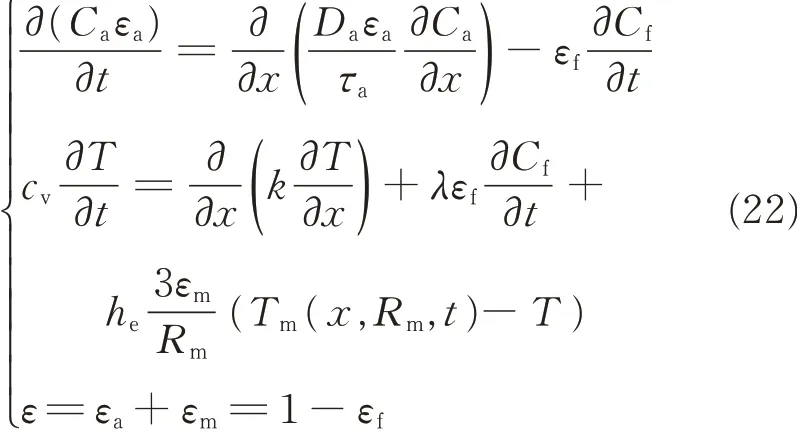
where εa,εf,and εmare the volumetric fractions of air filling inter-fiber space,fibers,and PCMs microcapsules,respectively. Cais the water vapor concentration in the air filling inter - fiber space,Cfthe mean water vapor concentration in the fibers of fabric,Dathe diffusion coefficient of water vapor in air,τathe effective tortuosity of water vapor through the fabric,and T the fabric temperature. cv,λ and k represent the volumetric heat capacity of the fabric,the heat of sorption of water vapor by fibers,and the thermal conductivity of the fabric,which are functions of the water content of the fibers respectively. heis the effective heat transfer coefficient between fabric and PCM,and Tm（x,Rm,t）the temperature at the surface of the PCM microcapsule,which is a function of position x of the PCM microcapsule in the fabric and time t.

The mean water vapor concentration in the fibers of fabric Cfcan be obtained by Fick’s Law［14］.Tm（x,Rm,t）can be obtained by solving the thermal balance equation for the PCM sphere［10］

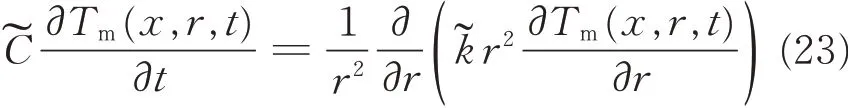
with boundary condition at the outer surface of the PCM microcapsule

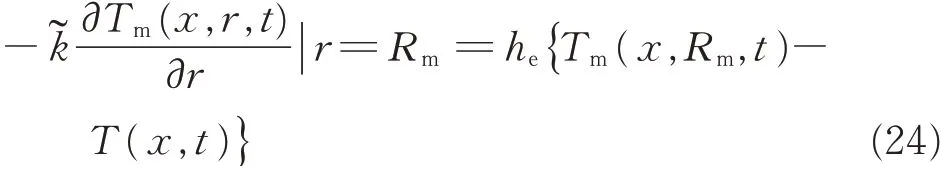
and that at the microcapsule centre

The initial condition of the PCM microcapsule is

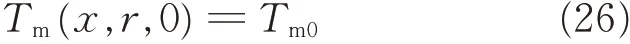
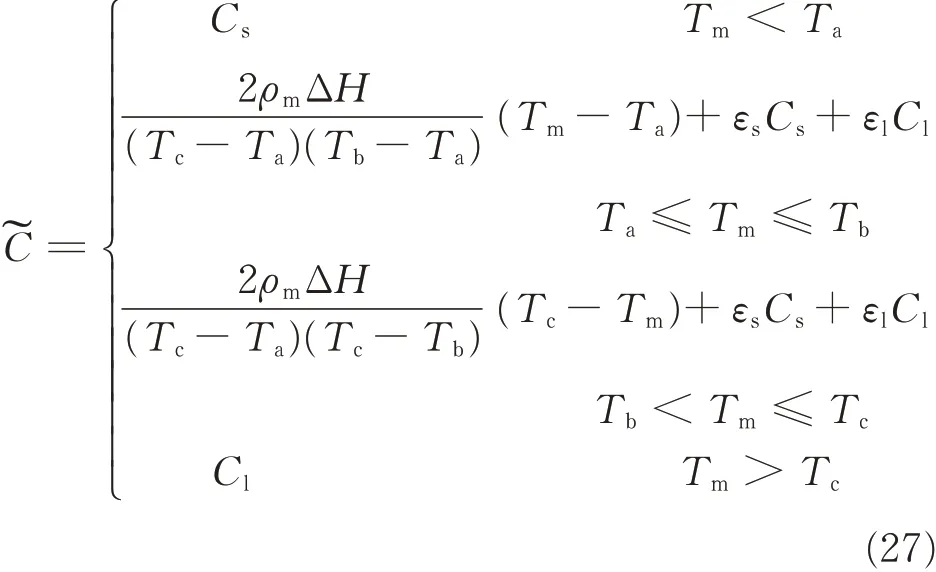
where Ta,Tb,Tcdenote characteristic temperatures for PCM. The phase transition of the PCM occurs over a temperature range［Ta,Tc］,where Taand Tcare the lower and the upper phase transition temperatures of PCM,respectively. Tbis the peak temperature,at which the variation rate of the apparent heat is zero. ΔH is the total latent heat in the phase change temperature range［Ta,Tc］. Cs,Clare the heat capacities for solid and liquid phase of PCM,respectively. ρmis the density of the PCM,and εl,εsare the volume fractions of the liquid and solid phase in mixture,respectively. Those can be determined according to the temperature and temperature range of the PCM.They can be expressed as

The effective thermal conductivity also can be expressed by the subsection function

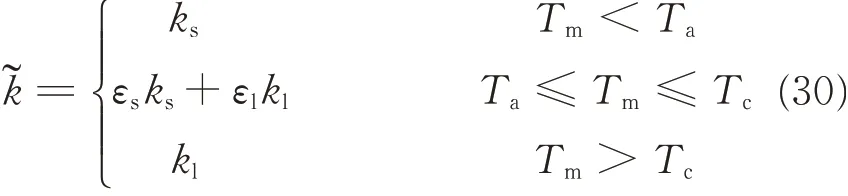
where ksand klare the thermal conductivities for solid and liquid phases of PCM,respectively.

1.3 Initial and boundary conditions between human body and clothing

To solve the above equations,the initial and boundary conditions must be listed. The initial conditions can be given by calculating the temperature and concentration at equilibrium state between clothing and environment. At the inner surface（x=0）of clothing near the i-th segment,the evaporation and conduction and radiation boundary conditions are considered. The equations of boundary conditions are

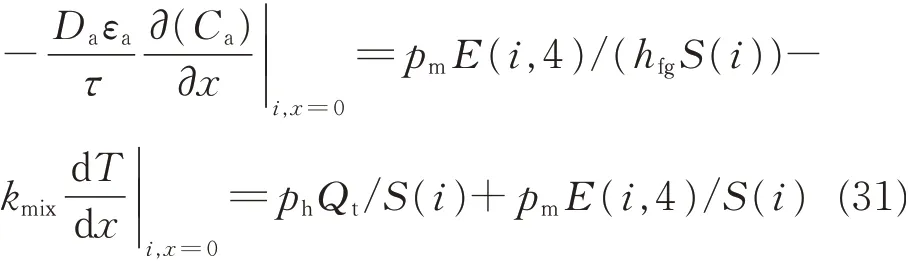
where pmand phindicate the proportion of moisture vapor and dry heat loss from the skin that passes through the inner surface of the clothing. At the outer surface（x=L）of clothing near the i-th segment,the convection and radiation boundary conditions are considered. The equations of boundary conditions are listed as follows

where Hmand Htrepresent the moisture and heat transfer coefficients. Ht=hr+hc. hris the radiation heat transfer coefficient. hcis the convective heat transfer coefficient,and it is a function of the air velocity v,for a seated person,hc=3.43+5.93v W/（m2·K）. The moisture transfer coefficient,Hm,is related to the convection heat transfer,and can be obtained from the Lewis Relation. Ca∞and T∞are ambient water vapor concentration and temperature,respectively.

2 Program Flow

The numerical technique for human body is explicit differential method,and that for clothing is implicit central differential method. The simulation program is written in FORTRAN and its flow chart is shown in Fig.1.

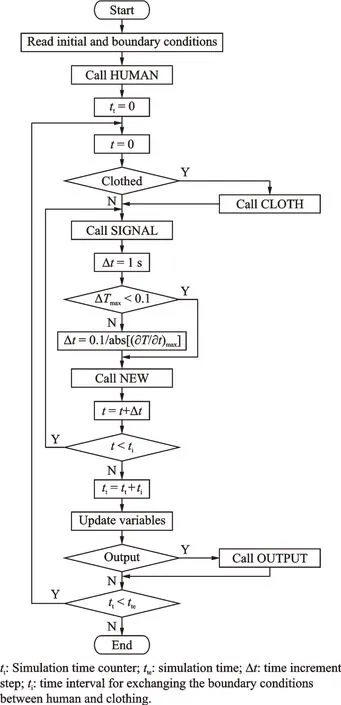
Fig.1 Flow chart of simulation program

The program consists of six parts：Main program,subroutines HUMAN,SIGNAL,CLOTH,NEW,and OUTPUT. Their functions are as follows：

Main program：Read initial and boundary conditions,control the program.

HUMAN：Read the physical parameters of the controlled system of human body and initial controlling parameters.

SIGNAL：Calculate the parameters of the controlling system and the heart-lung pool.

NEW：Update previous temperature.

OUTPUT：Prepare for the output of the simulation results.

CLOTH：Calculate the parameters of clothing.

3 Model Validation and Prediction

To validate the program and investigate the prediction ability of the model,the following experimental process is simulated.Initially,a person wearing the T-shirt with PCM microcapsules and cotton trousers sat on a chair in the room at 24.3 ℃,55.3% relative humidity（RH）and v=0.1 m/s for 20 min to reach an equilibrium state. Then,the experiment starts,the environment temperature falls.After 21 min,the environment temperature raises for 15 min. The variations of the environment temperature with time are shown in Fig.2. The temperatures at the skin surface and inner surface of clothing are measured. T-shirt is made of polypropylene and 5% PCM microcapsules. The phase change temperature range is［31.00 ℃,33.30 ℃］,and peak temperature Tb＝32.80 ℃. The radius of the microcapsules is 5 μm. Total phase change latent is 124 k J/kg. Other parameters of clothing can be obtained from Ref.［15］. The comparison of the model predictions and experimental measurements is shown in Fig.2,from which,we can see that the theoretical predictions and experimental data have a good agreement. In the process of increasing ambient temperature,the clothing and skin temperatures also increase due to the heating of environment. For about 27 min,the increase of clothing temperature is delayed due to the heat absorbed by PCM during the phase change process.

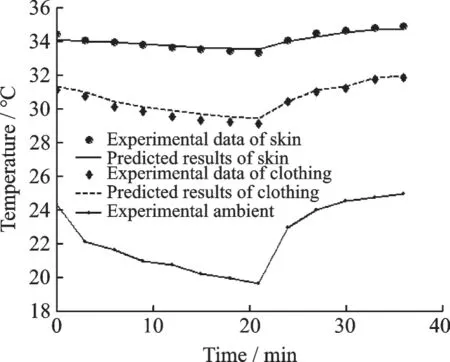
Fig.2 Comparison of model predictions and experimental data

Based on the validation of the model,the effects of the clothing with or without PCM,and fiber hygroscopisity on thermal responses of human body,the following protocol is simulated. In the first stage,the human body enters a cool room A（25oC,40% RH,0.3 m/s）,wearing the experimental clothing. The clothed human body sits on a chair in room A for 15 min to reach equilibrium state. Then,the experiment starts. The subjects move into a hot room B（36oC,80% RH,0.1 m/s）and stay in a seated position for 20 min.After that they return to room A again and have a rest for 40 min. Four types of the T-shirt are selected in simulation,which are cotton with 0% PCM,cotton with 20% PCM,polyester with 0% PCM and polyester with 20% PCM. In the simulation,the clothing thickness is 2.0 mm,and porosity is 0.90. The physical properties of basic materials can be found in Ref.［10］. The simulation results are shown in Figs.3-9.

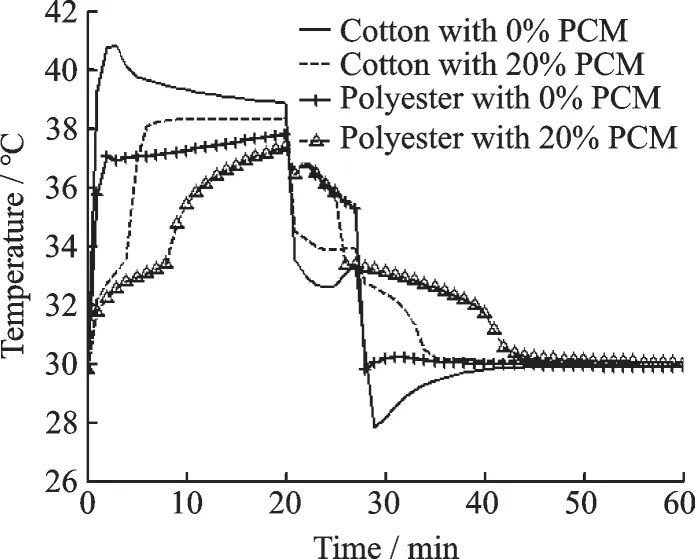
Fig.3 Temperature at inner surface of clothing near trunk

Fig.3 shows the temperature at inner surface of clothing near the trunk. Compared with the polyester garment with 0% PCM,the cotton garment with 0% PCM has the higher temperature increase in room B,and the larger drop in room A due to high hygroscopisity of the cotton fiber. The temperature increase at inner surface of cotton garment with 20% PCM is delayed from 0 min to 4 min in high environmental temperature,while that of the polyester garment with 20% PCM is delayed from 0 min to 10 min. This is because PCM is changing from solid to liquid and absorbing heat around the clothing when PCM gets to its changing temperature.The cotton fiber with high hygroscopicity releases larger sorption heat,which is absorbed rapidly by PCM,so the delaying time of PCM is short for the cotton garment. After the delaying time,PCM is not taking place phase change,and the temperature goes on increasing. In the low temperature and humidity environment,the temperature of clothing is decreasing until 21 min. Because of the decrease under environmental humidity,the evaporation heat from skin to clothing increases suddenly and so the temperature of clothing returns up. After that,the temperature of clothing goes on decreasing in low environmental temperature. Because the sweat accumulation on truck skin decreases to 0,the temperature of clothing and the evaporation heat from skin to clothing decreases suddenly around 27 min.When the clothing temperature reaches the phase change temperature range［31.00 ℃,33.30 ℃］,the PCM releases the latent heat,and the temperature decrease of garment with PCM is delayed. Finally,the temperature of clothing closes to the equilibrium with the surrounding. From Fig.3,we can see that the polyester garment with 20% PCM has longer temperature delaying time.

Fig.4 shows the temperature variation on the trunk skin surface. In the high temperature environment,the trunk skin temperature of the person dressed in clothing with PCM is lower and delayed obviously due to the effect of the PCM absorbing heat through melting,and the skin temperature of the person dressed in polyester with 20% PCM is the lowest. In low temperature environment,the temperature of skin returns up for a while due to the effect of the accommodation of blood,and the skin temperature of the person dressed in polyester with 20% PCM is the highest.

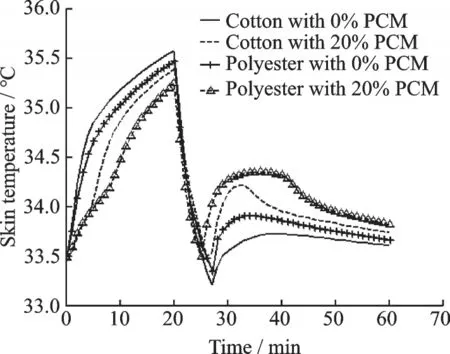
Fig.4 Temperature of trunk skin

Fig.5 shows the sweat rate on the skin surface.The change trend of the sweat rate is similar to that of the skin temperature. In high temperature environment,the sweat rate of the person dressed in polyester with 20% PCM is the lowest.

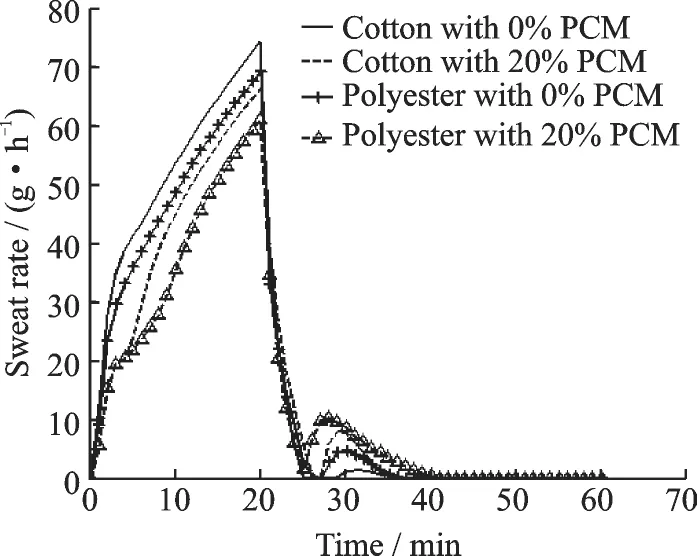
Fig.5 Sweat rate on skin surface

Fig.6 is the sweat accumulation on trunk skin surface. In high temperature environment,human begins sweating and the sweat accumulation increases at skin surface. In low temperature environment,the sweat accumulation decreases to 0. From Fig.6,we can see that inserting PCM into garment can decrease the time of sweat accumulation on skin surface. The time of sweat accumulation on trunk skin surface is the shortest when human is on polyester garment with 20% PCM.

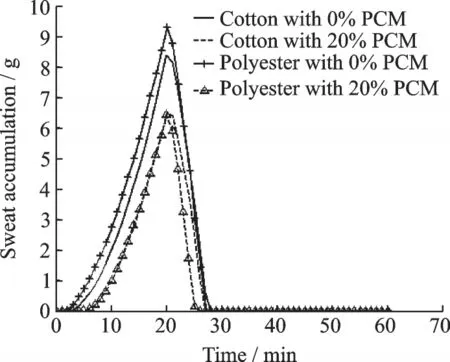
Fig.6 Sweat accumulation on trunk skin

Fig.7 shows dry heat loss from the trunk skin.Dry heat loss depends on the temperature difference between skin and clothing. In high temperature environment,dry heat loss is minus because the environment temperature is higher than skin surface temperature and body on clothing with PCM earns less heat than that on clothing without PCM from clothing. In low temperature environment,dry heat loss is plus because heat transfers from skin to clothing and at most time dry heat loss of body on clothing without PCM is more than that on clothing with PCM. From Fig.7 we can see that the absolute of heat loss for the person dressed in the polyester garment with 20% PCM is the lowest.

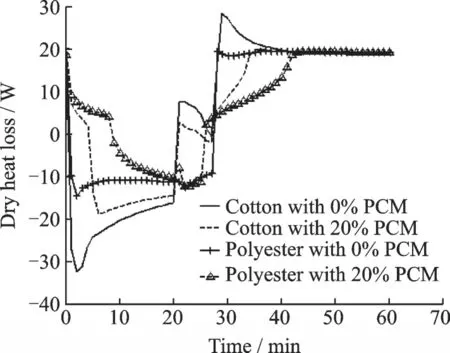
Fig.7 Dry heat loss of trunk skin

Fig.8 shows the evaporative heat loss from trunk skin surface. In high temperature environment evaporative heat loss at trunk skin surface on clothing without PCM is more than that on clothing with PCM. Evaporative heat loss varies directly as the water vapor pressure difference between skin surface and clothing inner surface. In high temperature environment,when the sweat accumulates on skin surface,the water vapor pressure of skin surface is saturated,which is related to the skin temperature directly. The skin temperature is higher,when person wears the garment without PCM. Therefore,the evaporative heat loss of the person dressed in garment without PCM is larger than that with PCM. The person with polyester garment with 20% PCM has the lowest evaporative heat loss in the high temperature environment. In low humidity environment,evaporative heat loss increases quickly because the water vapor pressure at clothing inner surface decreases quickly due to the lower environment humidity after 20 min. The skin saturated water vapor pressure decreases,as temperature of human,so evaporative heat loss decreases. Around 27 min,evaporative heat loss at trunk skin surface on clothing decreases quickly because the sweat accumulation at skin surface decreases to 0 and the water vapor pressure at skin surface decreases quickly.After 27 min. the evaporative heat loss of the person dressed in polyester garment with 20% PCM is the largest.

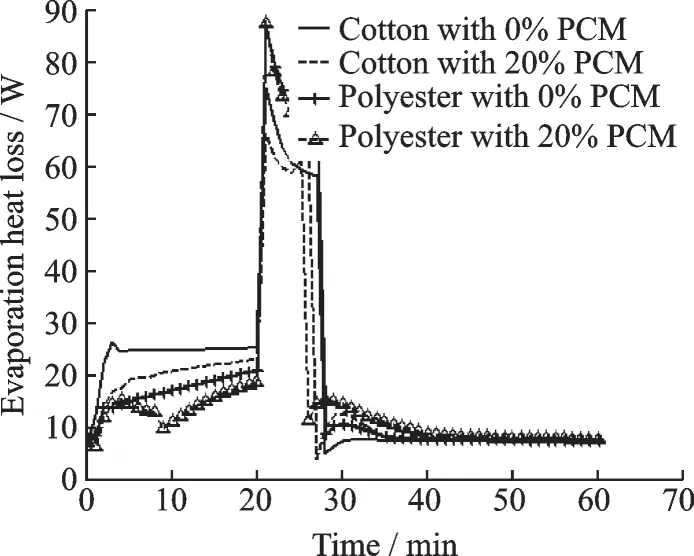
Fig.8 Evaporative heat loss at trunk skin surface

Fig.9 shows the heat exchange rate between blood and trunk skin. Because the temperature of blood is higher than that of skin,heat is transferred from blood to skin. In high temperature environment,the heat transferred from blood to skin on clothing with PCM is more than that on clothing without PCM,because at most of the time,the temperature of skin on clothing with PCM is lower than that on clothing without PCM. From Fig.9 we can see that at the most of the time,the heat exchange between blood and trunk skin of the person dressed in polyester garment with 20% PCM is the largest.

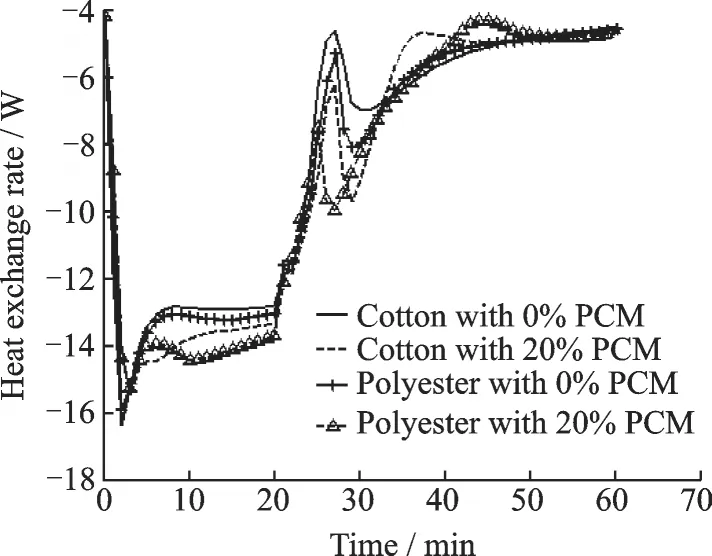
Fig.9 Heat exchange rate between blood and trunk skin

4 Conclusions

This paper discusses the influences of the PCM added in the clothing on heat and moisture in clothed human body by using the new model developed in this paper. Comparing the thermal responses of human body dressed in clothing with PCM and that without PCM,we can find that the PCM microcapsules in clothing can delay the raising of clothing temperature,decrease human body temperature and sweat accumulation on skin surface when human body is in hot environment,whereas,the PCM can delay temperature decreasing of the clothing and skin when the human body is in cold environment.Whether from high temperature and high humidity environment to low temperature and low humidity environment or the opposite environmental change process,fiber moisture absorption heat will reduce the delay effect of the PCM on the garment temperature. The model can provide a tool to analysis and design the thermal function of the garment with PCM.