Application of Fuzzy Bilateral Boundary DEA Model in Selection of Energy-Saving and Environmental Protection Enterprises

GENG Chengxuan,WANG Qiong,2*,E Haitao

1.College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,P.R.China；2.Aliyun School of Big Data,Changzhou University,Changzhou 213164,P.R.China

Abstract: The energy-saving and environmental protection industry has vast development space and huge market increment in China. Selecting appropriate energy-saving and environmental protection enterprises is one of the important decisions of venture capital investment. In the paper,a fuzzy bilateral boundary data envelopment analysis（DEA）model with optimistic coefficient is proposed to select those companies with high financing efficiencies. Based on the characteristics of enterprise financing,undesirable outputs and dual-role factors are considered in the proposed model. The results show that the fifth enterprise has high comprehensive financing efficiencies and always ranks the first when the optimistic coefficients are 0.2,0.5 and 0.8,respectively. In addition,most energy-saving and environmental protection enterprises have not efficient financing efficiencies. There is still much space for improvement.

Key wor ds: financing efficiency;double-frontier;dual-role factor;data envelopment analysis

0 Introduction

As the direction of a new round of technological revolution and industrial transformation,to accelerate the cultivation and development of strategic emerging industries is not only the general trend of global industrial restructuring but also a major strategic choice for the Chinese government to promote the transformation of economic development mode and upgrade the industrial structure. As one of strategic emerging industries,energy conservation and environmental protection industry in the future plays a more and more important role in the development of the national economy. In 1999,the proportion of investment in environmental protection was firstly above 1% in GDP. The proportion of environmental input to GDP increased from 1.2% during the 10th Five-Year Plan to 3.5% during the 12th Five-Year Plan. With the supply side reform and enforcement of tighter regulation in China,energy saving and environmental protection industry gradually open the market space. In 2017,the output value of energy conservation and environmental protection industry in China reached 1 trillion and 600 billion yuan. National Development and Reform Commission announced that its industrial scale is expected to double the original capacity to 2020 and become an important pillar industry of the national economy.

Capital is the core and artery of industry development. Annual capital demand of green industry in China is about 4 trillion yuan. The government,however,can only take out 10%,that is to say,about 90% of green investment funding gap rely on social and private capital. There are the characteristics of capital demand,long recovery period,and slow capital turnover in most energy conservation and environmental protection projects,which result in a lot of difficulties to obtain bank credit funds.Therefore,energy conservation and environmental protection companies are increasingly concerned about financing efficiencies under the limited financial resources supplied. Improving financing efficiencies helps to promote industrial quality and efficiency as well as industrial transformation and upgrading. At the same time,selecting energy saving and environmental protection companies with high financing efficiencies are the best choice for venture capital enterprises.

In this paper,we employed a fuzzy double-frontier data envelopment analysis（DEA）model with undesirable outputs and dual-role factors for evaluating financing efficiencies of energy saving and environmental protection companies. This model can present comprehensive fuzzy efficiencies considering both the magnitude and direction of optimistic and pessimistic fuzzy efficiencies calculated by fuzzy operation nature,and then rank them by preference degree and optimistic coefficient. Further,it can provide not only the ranking of these financing efficiencies but also the extent to which any company is superior to another.

1 Literature Review

Since Zeng first proposed the concept of financing efficiency in 1993［1］,many scholars began to research on financing efficiency.There are many methods to evaluate the financing efficiencies of companies. As one of them,DEA,first proposed by Charnes et al. in 1978［2］,is a non-parametric approach to measure best relative efficiencies of decision-making units（DMUs）. A decision-making unit is considered as effective if its efficiency is equal to unity；otherwise,it is inefficient. The DEA method does not require any assumptions about the shape of the production frontier level and the internal operations of the decision-making units. It has been successfully and widely used in various fields,such as health care,energy,finance,education,utilities,etc.

Conventional DEA measures the best relative efficiencies of all decision making units with respect to the efficiency frontier. These efficiencies are also called optimistic efficiencies. DEA model with double frontiers,first proposed by Wang et al.［3］,considers both optimistic efficiencies with respect to efficiency frontier and pessimistic efficiencies with respect to inefficiency frontier. By evaluating only the best efficiency of all decision-making units,the conventional DEA model cannot provide an overall assessment of them. Futrher,they can be fully ranked if we have optimistic and pessimistic relative efficiencies by double frontiers. Later,in 2009,Wang et al. converted fuzzy DEA models into three linear programming models by fuzzy arithmetic and obtained the fuzzy efficiencies of all decision-making units［4］. Ahmady et al. developed fuzzy DEA models with double frontiers［5-6］.

Basic DEA models require crisp inputs and outputs. In the real world,however,the observed values of both inputs and outputs may not always be accurate,especially when DMUs contain missing or judgment data. After Sengupta proposed a fuzzy approach in DEA［7］,many fuzzy DEA methods have been developed. The most common method of fuzzy DEA model is the approach of using α-level cut set,in which the fuzzy DEA model can be transformed into a pair of mathematical programming to obtain the upper and lower bounds of α-level cut sets of efficiency scores,such as Kao and Liu［8］. Guo et al.firstly proposed fuzzy DEA models by the possibility and necessity measures in 2000［9］. Subsequently,Lertworasirikul et al. presented two ranking methods in fuzzy DEA models with possibility and necessity approach in 2003［10］. In the above mentioned DEA approaches,it is assumed that all the outputs are desirable in efficiency analysis. But there are sometimes undesirable outputs in our real world,such as financing risk. In 2002,Seiford et al. proposed a DEA model with undesirable factors in efficiency evaluation［11］. The undesirable outputs should be decreased to increase efficiency. Jahanshahloo et al. proposed a DEA model with double frontiers in the presence of undesirable outputs in 2005［12］. And Toloo et al. presented individual and summative models in the DEA model with undesirable outputs［13］. More desirable outputs relative fewer inputs are preferred in the DEA model. Undesirable outputs are always accompanied by the increasing desirable outputs in the production process.Therefore,this model considers undesirable outputs as inputs［14］.

Besides undesirable outputs,there might be some variables as both inputs and outputs. These variables are called dual-role factors. For instance,to evaluate financing efficiencies,a variable like financing cost,can be considered as both an input and an output. Such a factor is input since it is also part of inputs in the financing process. And it plays a role of outputs because it is accompanied with inputs.Cook et al. proposed a DEA model with dual-role factors［15］. Azadi et al. developed a DEA model in the presence of both undesirable outputs and dualrole factors to select the best green suppliers［16］. The idea of this model is to convert the fuzzy DEA model to the classical DEA model by fuzzy expected values,which lose some information about the sample.

2 Fuzzy Bilateral Boundary DEA Model

A new fuzzy DEA model with double frontiers is proposed in this section,which considering both dual-role factors and undesirable outputs. To this end,we employ the traditional DEA model,which was proposed by Charnes et al. in 1978 and described as follows［2］

where θ0denotes the efficiency of DMU0under investigation；xi0the i th input of DMU0,and yr0the r th output；viand urare the weights of input xijand output yrjof DMUj,respectively.DMU0is considered to be efficient if θ0=1,and inefficient if θ0＜1. This linear programming is equivalent to the following

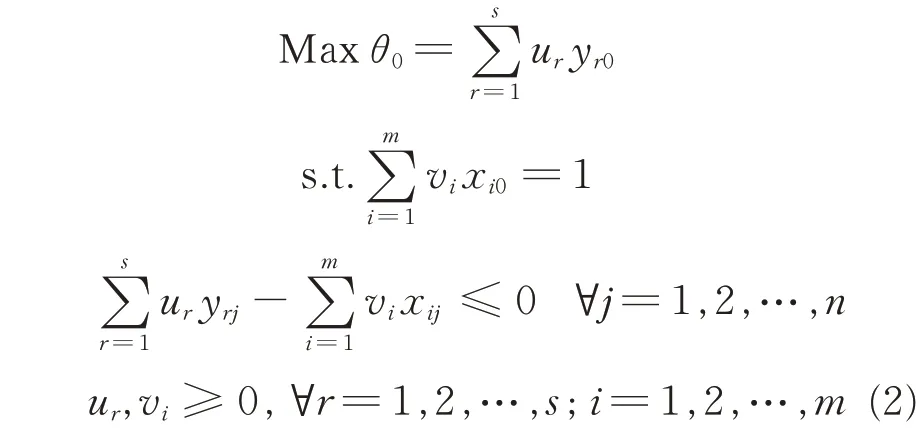
The efficiency θ0of DMU0obtained from Eq.（2）by maximizing in the range of not greater than 1,is the optimistic efficiency relative to the other decision-making unit. All optimistic efficient units form an efficient production frontier. If by replacing the maximum to the minimum,the efficiency of any decision-making unit is required to be greater than or equal to 1,and then the efficiency is called the worst relative efficiency. It is also called pessimistic efficiency. These pessimistic inefficient efficiencies form an inefficient production frontier. The specific model is as follows

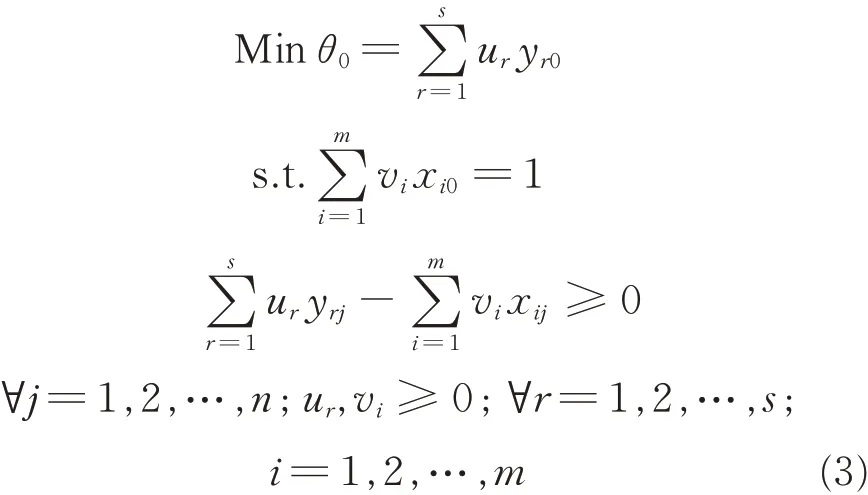
2.1 Optimistic fuzzy r elative efficiencies

Suppose that there are n decision-making units for assessment,each decision-making unit consists of m inputs and s outputs. Let the input and output values of the j th decision-making unit be characterized by triangular fuzzy numbersandwithand(i=1,2,…,m； j=1,2,…,n;r=1,2,…,s),respectively. Ifandanddegenerate into crisp values as a special case of triangular fuzzy data. And the specific description of variables is shown in Table 1.

Table 1 Variable description

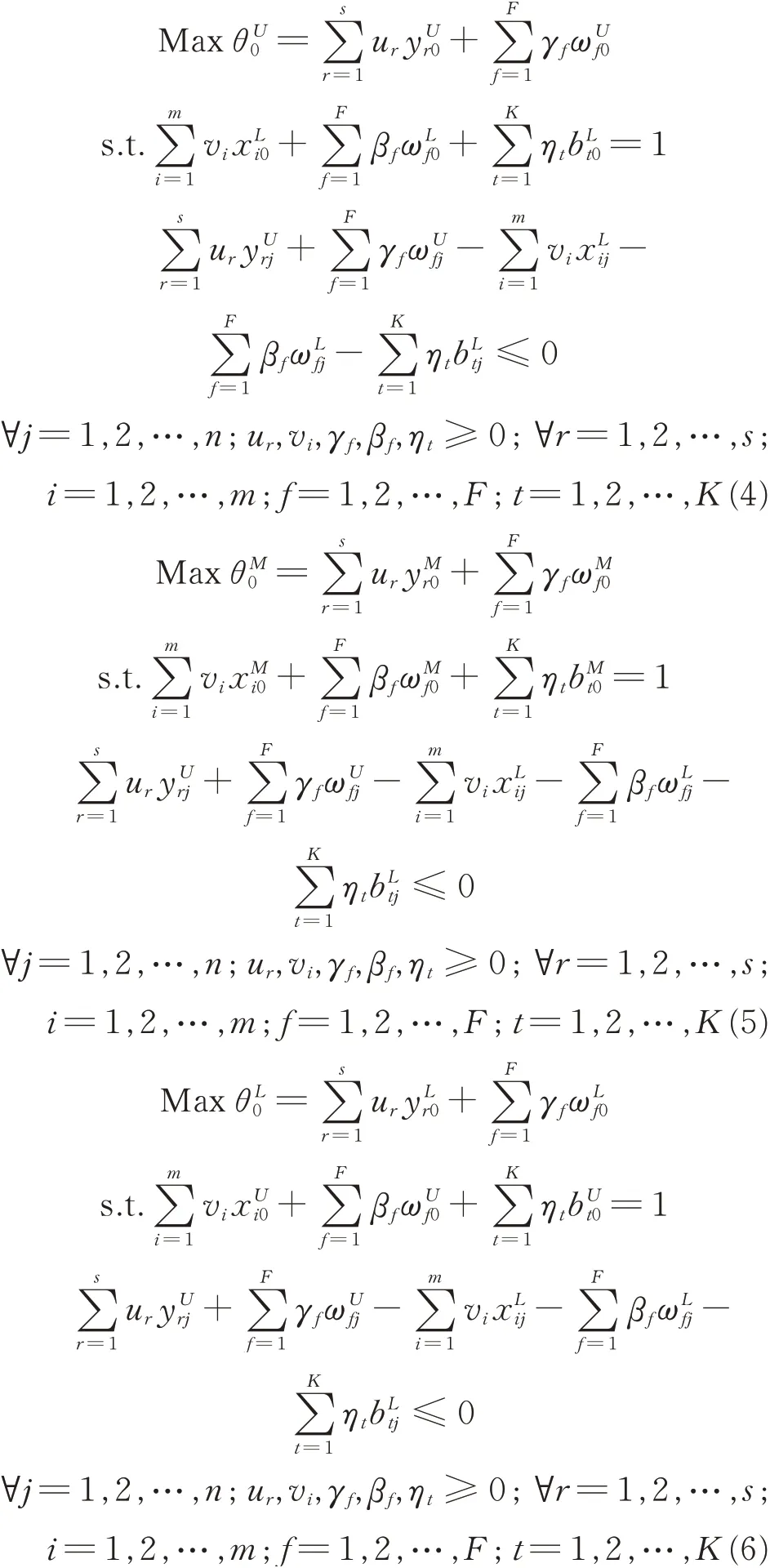
The optimistic fuzzy efficiencyof the decision-making unit under investigation consists of optimal values obtained from the above models（4）—（6）,almost regarded as a triangular fuzzy number. If θU*0is equal to 1,the decision-making unit under investigation is called optimistic efficient or fuzzy DEA efficient. All these fuzzy DEA efficient decision-making units form an efficiency frontier.

2.2 Pessimistic fuzzy r elative efficiencies

In the pessimistic case,the output level is maintained in the current limit,while input values are proportionally increased until reaching the inefficient production frontier. The efficiency for the inefficient production possibility set obtained from DEA model is called the worst relative efficiency or pessimistic efficiency.

Theor emThe pessimistic fuzzy efficiencyof DMU0with dual-role factors and undesirable outputs are obtained from the following programming models

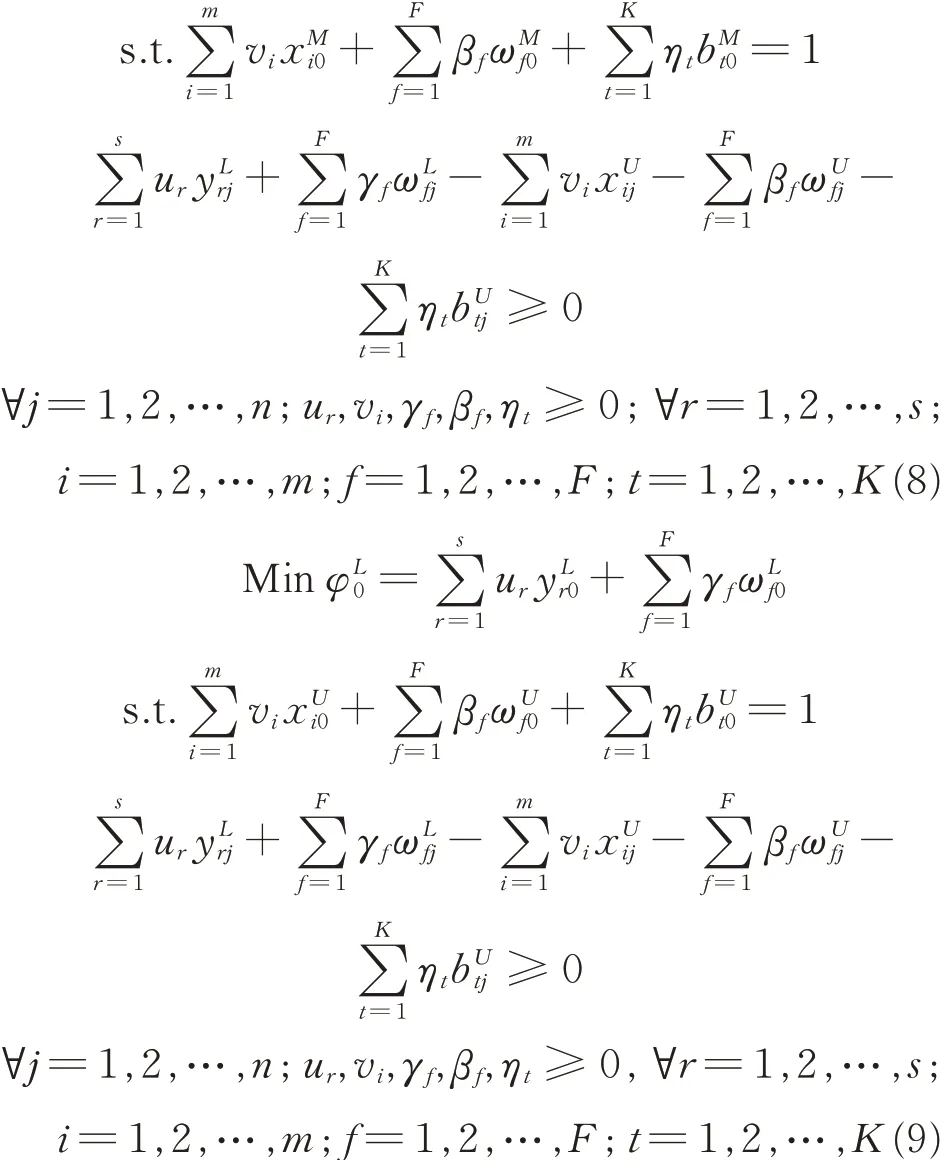
The pessimistic fuzzy inefficiencyof the decision-making unit under investigation consists of three optimal values obtained from Eqs.（7）—（9）,which can be almost regarded as a triangular fuzzy number. If,this decision-making unit under investigation is called pessimistic inefficient or fuzzy DEA inefficient. All these fuzzy DEA inefficient decision-making units form an inefficiency frontier.

2.3 Compr ehensive fuzzy efficiencies with bilater al boundar y

From two different perspectives,we can obtain optimistic and pessimistic fuzzy efficiencies. Then there are two different rankings for each decisionmaking unit. Naturally,we need a comprehensive performance measure for each DMU. Here,we propose the following measure based on Wang et al.［4］for evaluating all decision-making units rather than other means

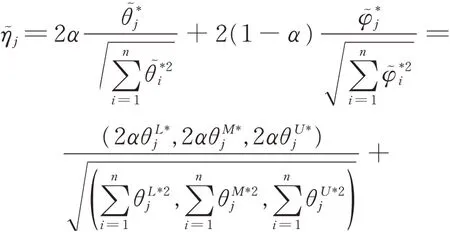
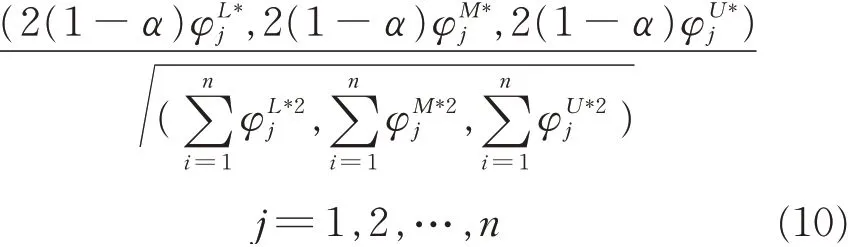
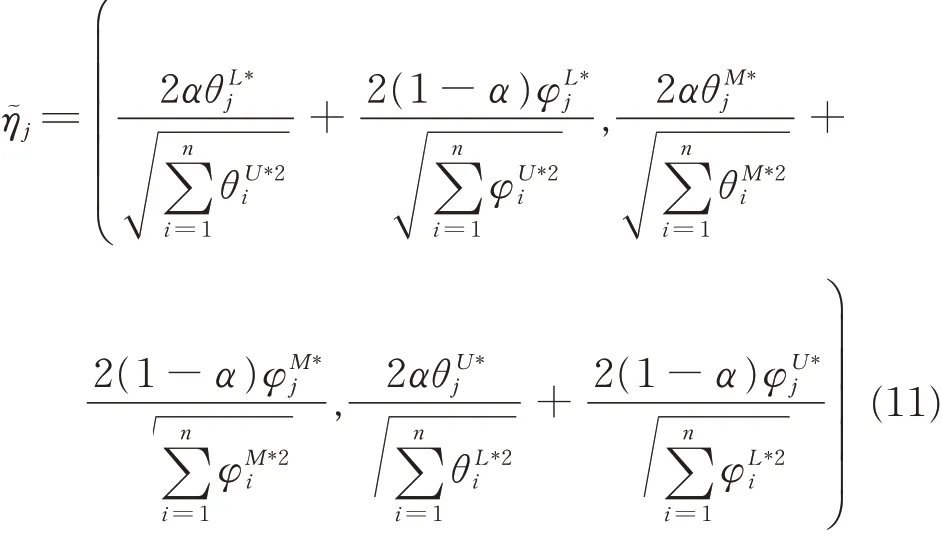
The optimistic fuzzy efficient decision-making units on the efficiency frontier have good performance relative to other decision-making units,while those on the inefficiency frontier have relatively poor performance. The best decision-making units can usually be derived from the optimistic fuzzy efficient decision-making units. Since the comprehensive fuzzy efficiencyis a triangular fuzzy number,we can compare and rank all comprehensive fuzzy efficiencies with the degree of preference approach in the next section.

2.4 Ranking methods of fuzzy triangular efficiencies

There are many methods in the current literature for ranking fuzzy numbers. In this paper,a preference degree will be introduced for ranking fuzzy triangular efficiencies of decision-making units.

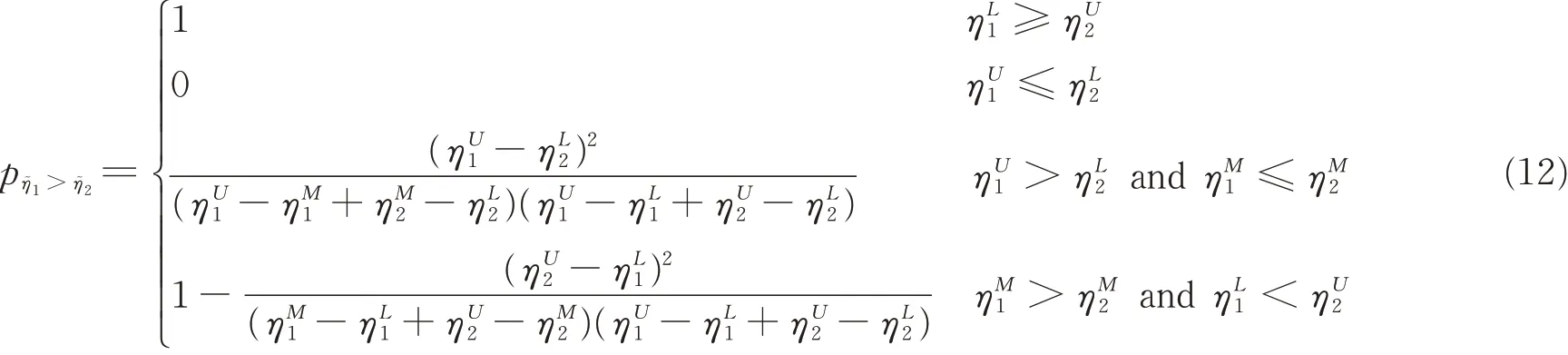
We can calculate the preference degree for any two decision-making units,which constitute the matrix of preference degree. If we find the j th row of this matrix with all elements being not less than 0.5,the fuzzy efficiency ñjis the highest. After eliminating the j th row and column of preference degree matrix,searching for the biggest efficiency is repeated until all triangular fuzzy efficiencies are fully ranked.

3 Selection of Energy Saving and Environmental Protection Enterprises

3.1 Data resource

In this section,we applied the proposed model to 19 listed enterprises of energy conservation and environmental protection industry in China. The financing sources of enterprises are debt financing and equity financing. Accordingly,the inputs include debt financing and equity financing［17］. The amount of debt financing is indicated by the sum of shortterm loans,the bond payable and long-term loans.And the amount of equity financing is indicated by the sum of paid-in capital,capital reserve,surplus reserve,and undistributed profit. The amount financed is not a one-off gain at the beginning of the year,thus these inputs are considered as triangular fuzzy numbers according to their financing amount at the beginning,middle and end of the year. Financing cost can be regarded as the output of financing capital and the input of the operation with financing capital. Then indicated by the sum of dividends and interest payable,the financing cost is selected as a dual-role factor in the form of a triangular fuzzy number. The final performance on financing efficiency of enterprises includes the market performance and management level. The net profit and prime operating revenue are considered as desirable outputs,in which prime operating revenue is regarded as a triangular fuzzy number due to the uncertain environment and time. The equity ratio is a major factor that affects the financial risk of enterprises. Indicated by equity ratio,financing risk is the only undesirable output and also regarded as a triangular fuzzy number due to the uncertain environment. The related data are derived from the financial statements of listed companies in the CSMAR database,as shown in Table 2.

3.2 Results

By solving the models（4）—（9）for the j th decision-making unit（j=1,2,…,n）,we can obtain its optimistic fuzzy efficiencyand pessimistic fuzzy efficiency,as shown in Table 3. According to Table 3,11 companies with efficienciesare optimistic fuzzy efficient or DEA efficient. And other companies with efficienciesare not optimistic efficient. These optimistic fuzzy efficient companies together form an efficiency frontier. The minimum of all upper boundsis only 0.424 7 and that of all lower boundsis 0.271 1. The optimistic fuzzy efficiency of DMU10is equal to unity,which means it is DEA efficient.

However,from the pessimistic perspective,14 companies with efficienciesare pessimistic fuzzy inefficient and DEA inefficient. Then these companies form an inefficiency frontier. Other companies withare fuzzy pessimistic non-inefficient. Therefore,optimistic and pessimistic fuzzy efficiencies are the extreme cases of financing efficiencies and have two different relative efficiency frontiers. The financing performances of all companies are between these two frontiers. We can easily see that some companies are on both frontiers. Therefore,it is necessary to consider the bilateral boundary method to evaluate the financing performance ofcompanies.

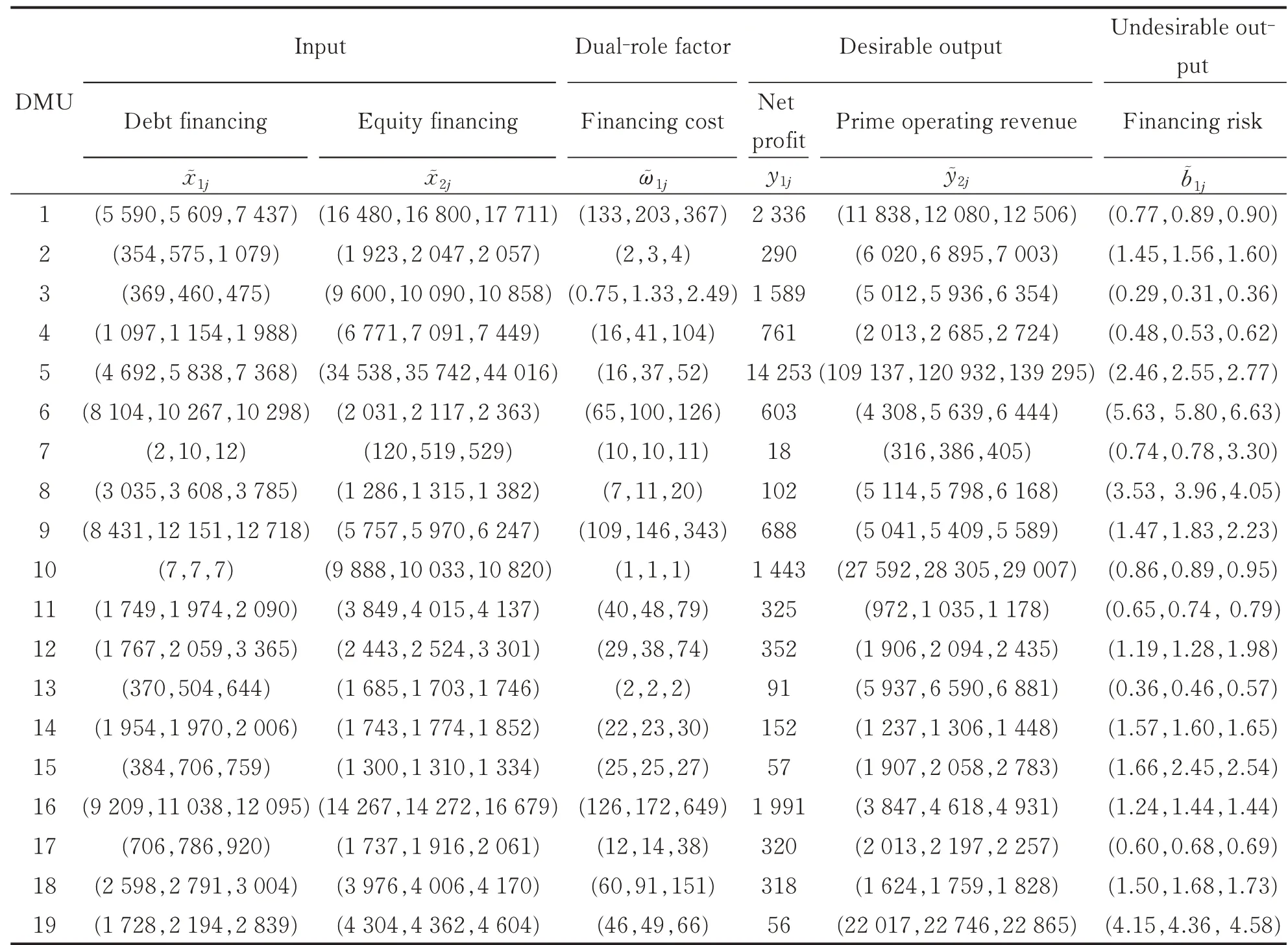
Table 2 Sample dataset of energy saving and environmental protection companies

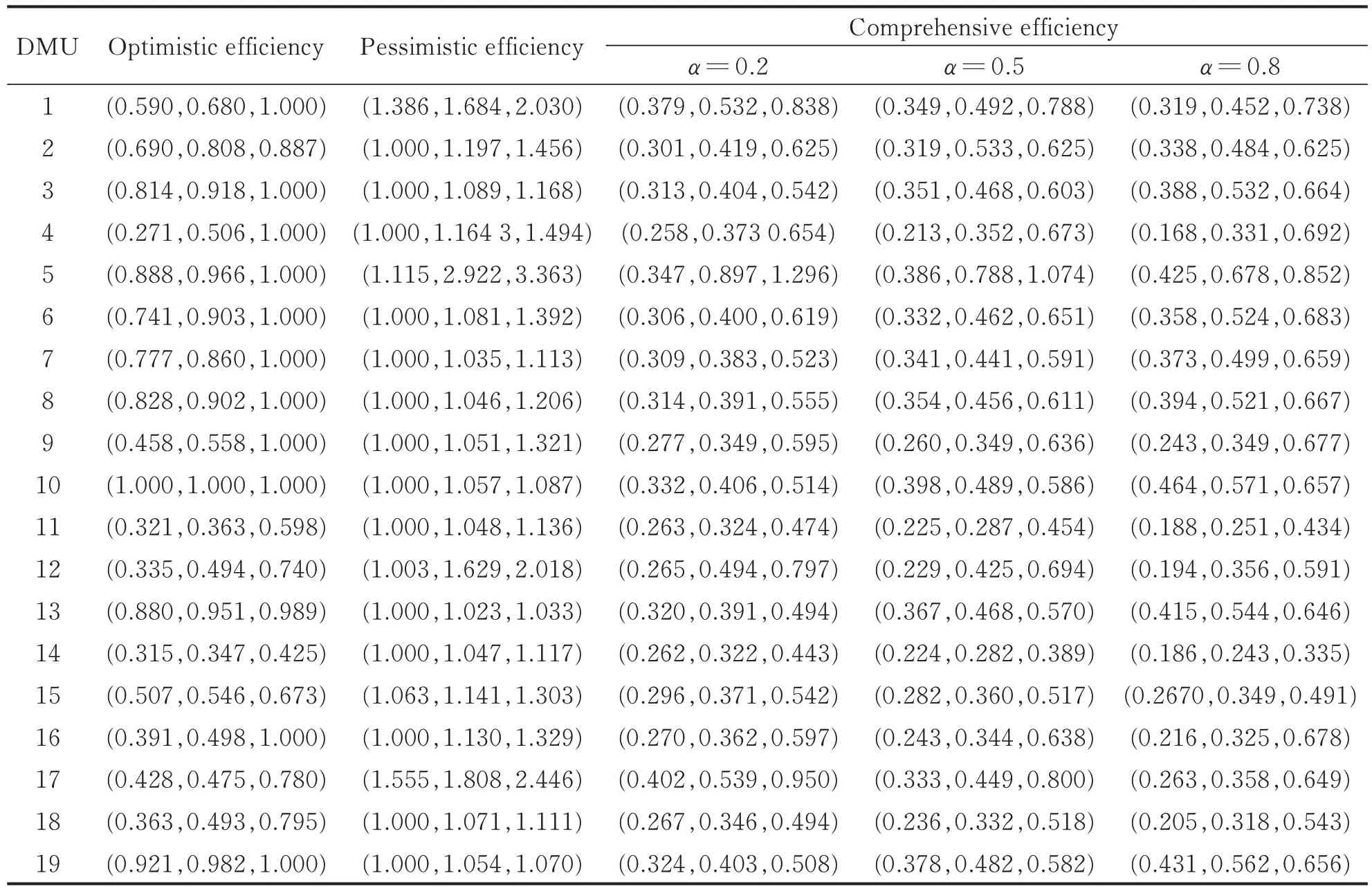
Table 3 Fuzzy financing efficiencies for 19 companies

To provide a full ranking for these companies from different perspectives,Table 4 shows preference degree and their rankings for optimistic,pessimistic and different comprehensive fuzzy efficiencies. In Table 4,these companies are fully ranked from the optimistic perspective asmeans that the former performs better than the latter to the extent of 64%. But they have ranked from the pessimistic perspective as13. In Table 3,it can easily see that DMU1is optimistic efficient and not pessimistic inefficient,while DMU2is just the opposite.Moreover,DMU2has better performance than DMU1according to optimistic fuzzy efficiencies,while it is opposite in the pessimistic case. Obviously,there is an inconsistency between the two rankings for these companies. It is due to considering only one perspective,such as the best or the worst situation. The results obtained by using different models are usually not the same.It explains that the evaluation ranking considering only one perspective may be unilateral,impractical and non-persuasive.

In order to take both frontiers into account,the solution is to consider both the magnitude and the direction of optimistic and pessimistic fuzzy efficiencies. Therefore,we need to introduce an optimistic coefficient α to get different comprehensive fuzzy financing efficiencies calculated by models（11）—（12）. Specific comprehensive fuzzy efficiencies with α=0.2,0.5 and 0.8 are shown in the right columns of Table 3. We can see that these fuzzy efficiencies are very low and the minimum of all upper bounds is 0.335. But the upper bounds of ηU5with α=0.2 and 0.5 is greater than 1.

The rankings and preference degrees with different optimistic coefficient are shown in the right columns of Table 4. The results show the financing performance and rankings of companies from different perspectives. From the optimistic perspective,the 10th company has the best performance. But the5th company has the best performance from the pessimistic perspective and with optimistic coefficient α=0.2,0.5 and 0.8. Moreover,we also know the preference degrees. For example,when α=0.2,the comprehensive financing performance of DMU5is 75% more than that of DMU17.

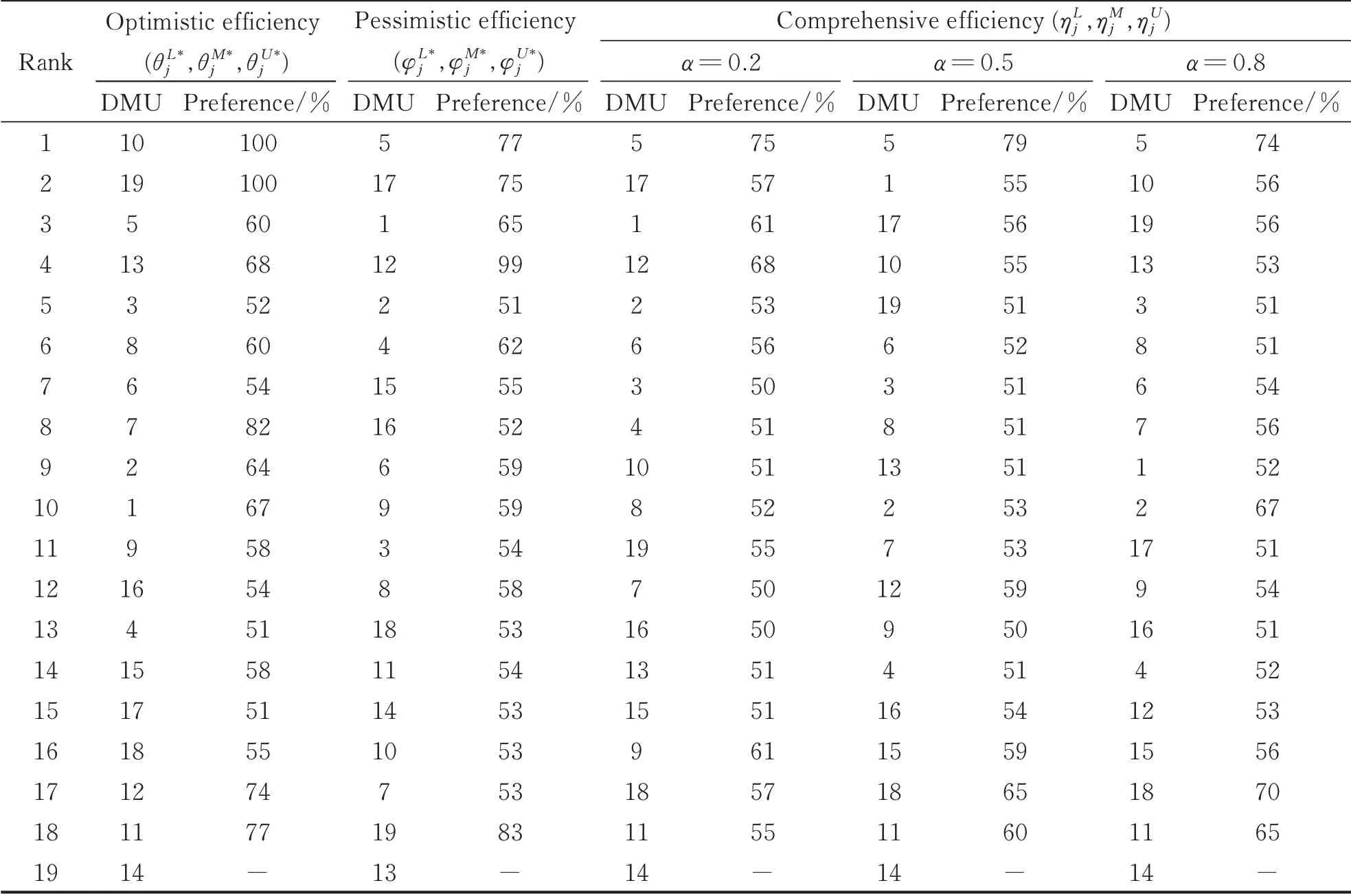
Table 4 Prefer ence degrees and r ankings for 19 companies

4 Conclusions

The whole process of enterprises’business financing is full of uncertainty,including financing cost and risk,etc. In recent years,environmental protection finance has a great impact on energy saving and environmental protection industries. Competition between environmental protection enterprises has intensified and gradually evolved into competition and cooperation between these enterprises and financial institutions. Therefore,high financing efficiencies have become a new competitive factor for energy saving and environmental protection enterprises. To select an energy saving and environmental protection enterprise with high financing efficiencies as investment targets,we employed the fuzzy double-frontier DEA model to evaluate and rank the financing efficiencies of enterprises in this paper. We took into account the fuzzy DEA approach with double frontiers combined with fuzzy arithmetic and preference degree. It avoids loss information when transforming fuzzy programming into classical mathematical programming.

Relative to the optimistic efficiency frontier,financing efficiencies of some companies are efficient,but not efficient relative to the pessimistic efficiency frontier. This model considers not only the magnitude but also the direction of optimistic and pessimistic fuzzy efficiencies of all decision-making units.Moreover,it introduced an optimistic coefficient to obtain different comprehensive fuzzy financing efficiencies. And it can provide the full ranking of all enterprises as well as the priority information calculated by preference degree and optimistic coefficients.It also offers a new perspective for the evaluation of other performance.