基于随机动力系统的证券市场演化动态研究

赵鹏举,张 维

(1.天津大学管理与经济学部，天津 300072；2. 中原工学院系统与工业工程研究中心，河南 郑州 450007；3. 中国社会计算研究中心，天津 300072)

1 引言

Alchian[1]和Friedman[2]提出了一个命题，认为市场使追求回报最大化的参与者生存下来。在其思想基础上，Fama[3]在其论述EMH假定的一篇经典文献中，对套利行为分析得出如下结论：由于理性交易者的套利行为，非理性交易者从长期看必定是亏损的，最终会在金融市场中消失，从而金融市场终将是有效的。

Fama等人的论证事实上预设了市场有效性的假定，从而理性交易者的套利行为才能从长期上使非理性交易者因持续亏损而退出市场。事实上，这是一个在理性预期前提下的循环论证。如果市场并非完全有效，则理性预期下的套利并非是无风险的。而理性交易者也并非是稳定市场的力量。此外，即使作为个体的非理性交易者会持续亏损，在长期趋向上终将退出市场，然而，还会有新的非理性交易者不断地进入市场。非理性交易者作为一个总体是否会在金融市场上消失还需严格的定量分析。因而，如何描述这两类交易者增减变化的动态规律，成为量化分析证券市场演化的关键问题。

Fama等人对市场演化的论证都是定性的，直到上世纪90年代初期, Blume和Easley[4]最先对市场选择假说对其进行了定量分析，他们提出了一个演化模型，通过推导得出了最适者生存的结论。此后，出现了一系列研究市场演化问题的量化模型，这些文献的结论却是两分的。

对市场演化大问题的研究结论大致可以分为两类，一类认为在一定前提下，市场演化能够达到理性均衡。Evstigneev等[5]建立离散时间模型讨论了金融市场稳定进化的充分必要条件，证明了在股票价格与未来股息收益贴现值的数学期望相等时，证券市场能够稳定进化到理想状态。我国学者杨招军和秦国文[6]在Evstigneev等人工作基础上，研究了连续时间模型的金融市场进化问题。研究结果显示采用买入资产相对股息大于相对股价的股票策略，在投资者初始财富大于零的前提下，最终将控制市场上的所有财富。龙张红等[7]用中国股市数据对金融进化论进行了实证研究，验证了扬招军和秦国文等人的观点。Akbas等[8]的研究结果认为对冲基金(智钱，Smart money)能够纠正市场中的错误定价。

另一类认为在一定条件下，非理性交易者也可以生存。Blume和Easley[9]在2006年进一步讨论了市场选择假说。其研究结果证明市场选择假说存在疑问，当市场不完备时，理性交易者也可能被淘汰。

同时，一些学者对市场淘汰非理性交易者的假定进行了研究。Bruno和Raphael[10]的研究认为，由于非理性交易者会高估或低估红利，并且他们“固执”地相信自己的判断，从而客观上提高了非理性交易者的讨价还价能力，使得非理性交易者可能获得高于理性交易者的收益。基于此，Bruno和Raphael[10]分析了非理性交易者动态演化过程，并得出非理性交易者可以在证券市场中长期生存的结论。张永杰等[11]的研究也认为价格内生同时存在套利限制时，市场无法淘汰噪音交易者、反馈交易者等类型的非理性交易者。

市场演化的长期均衡问题仍然是一个未定的问题，而且也是新古典金融学与行为金融学争论的焦点之一。以往研究在两个方面上存在着改进的必要：一是以上研究将市场视为一个封闭系统，期间未考虑新进入者对各群体的影响。事实上，即使某类个体由于采用了不适宜的交易策略而逐渐被市场淘汰，而由于新进入者的影响，该类个体的种群可能仍然在市场中存在并对市场产生影响；二是为了简化研究通常采用了市场价格外生的假定。而目前有大量研究结果显示，交易者行为与市场价格存在交互作用，大量非理性交易者的存在会导致市场价格偏离理性均衡价格，从而导致理性交易者的亏损。在证券市场上，这意味着大量涌入的非理性交易者可能会破坏证券市场的效率，从而改变市场演化发展的过程。扈文秀等[12]分析了非理性交易行为对资产价格所产生的影响，说明了资产价格泡沫与非理性交易行为之间的关系。刘燕和朱宏泉[13]的实证研究也证明个人投资者的异质信念会左右市场定价。Shirokikh等[14]用基于秩相关的网络模型研究了美国股票市场的演化问题，认为交易者的协同交易行为与市场波动存在关系。

对不同类型交易者收益率的研究也证明了理性交易者并非总能获取高于市场的收益率。例如Cochrane[15]研究了1994- 2010年间美国全部对冲基金的平均收益率，结果显示其收益率经常低于市场收益率，在2009年左右更是低至-40%以下。

赵鹏举[16]建立了一个微分动力系统模型来刻画市场演化动态，该模型吸收了生物种群动力系统中的有益成分，有很好的可扩展性，可以很方便的将新进入者的影响纳入市场选择假说的讨论中来，同时还能够通过对参数的设定，考虑价格内生等因素对市场演化短期动态和长期均衡的影响。但该模型是确定性模型，而在真实的证券市场中，任意时刻交易者的财富，证券市场收益，市场的净进入率等变量和参数都是随机的。因而，有必要将该模型扩展为随机动态模型进行分析。

Lo A W[17]依据有限理性假定和生物进化理论提出适应性市场预期(AMH, Adaptive Markets Hypothesis),将金融市场看作一个生态系统，存在捕食者和被捕食者，二者相互依存，数量动态变化。本文将借鉴这个思想构建基本的模型框架，将交易者分为理性交易者和非理性交易者，建立随机动力系统模型，刻画证券市场演化规律。通过对模型的分析来分析的不同类型交易者财富变化的动态轨迹和市场的长期均衡。

2 演化模型

考虑有理性交易者和非理性交易者参与的市场，假定在t时刻，理性交易者的财富总额为xt，非理性交易者总额为yt，两者的收益率分别为rx和ry，显然，当市场全部为理性交易者的情况下，rx即为市场收益率。同理，当市场全部为非理性交易者的情况下，ry即为市场收益率。依据Alchian[1]和Friedman[2]的断言，当市场由理性交易者和非理性交易者共同构成时，理性交易者总是能获得高于市场平均的收益率，并逐渐将非理性交易者逐出市场，因而随着非理性交易者减少以至到灭绝，理性交易者的收益率将递减至市场平均收益率，即rx和ry取决与市场中两类交易者的比例，因而可以得到描述演化动态的微分方程组；

(1)

其中θ1,θ2是参数向量。

2.1 作为封闭系统的市场演化模型

为简化问题，首先假定市场中没有新的进入者，即市场作为一个封闭系统进行研究。当市场是一个封闭系统时，两类交易者财富总量变化动态的微分方程组如下：

(2)

设证券市场收益率为rm，显然有：

xt·rx+yt·ry=(xt+yt)·rm

(3)

考虑到随着理性交易者财富在市场中的比例逐步提升，其收益率将下降，因而rx应当具备以下性质：

(1)理性交易者收益率随其占市场比例的增加而减少，且凸向原点。

双曲函数具备以上典型特征，因而设rx为双曲函数，即：

(4)

结合以上公式(3)和(4)可以得到：

(5)

rm和α是参数，从公式(5)中可以明确看出α的含义，就是理性交易者对非理性交易者的掠夺率。进一步，由(2)和(5)可以得出描述市场演化动态的微分动力系统为：

(6)

其中，xt表示理性交易者t时刻的财富总额，yt为非理性交易者t时刻的财富总额，两者的收益率分别为rx和ry，rm为市场收益率，α代表理性交易者对非理性交易者的掠夺率。

从市场整体的视角来看，不同时间区间市场收益率和掠夺率是随时间随机波动的，但本文关注的重点是给定市场结构前提下两类交易者财富的变化动态，给定一段时间区间的证券市场，必定存在一个rm和α的均值，因而这里的市场收益率和掠夺率假定为给定一段时间区间后的平均值，并作为参数处理。

2.2 开放系统市场演化动态模型

显然，证券市场作为一个开放系统，不断的会有新的交易者进入市场，也会有交易者退出市场，将两者的作用简化为一个净进入率纳入模型可以更加完整和准确的描述市场演化的动态轨迹。

结合对证券市场新进入者的实证分析，可以设某一时刻理性交易者和非理性交易者进入市场的速度与两类交易者的存量财富之间存在线性关系，即理性交易者的在t时刻进入市场的财富为ex(xt+yt)，非理性交易者的在t时刻进入市场的财富为ey(xt+yt)，其中ex，ey分别是理性交易者和非理性交易者的净进入率。这个假定称为线性进入的假定，在证券市场发展的初级阶段，这个假定可以描述证券市场两类交易者进入市场的动态过程。

因而可以得到描述作为开放系统的证券市场演化动态的微分方程组；

(7)

其中rm,α,ex,ey是参数，考虑各参数的经济含义，显然在现实的证券市场中存在rm,α,ex,ey≥0。模型构建的详细分析参见赵鹏举。

2.3 开放市场随机演化动态模型

由于两类交易者的财富总额显然是随机的，因而将上述模型推广为随机模型。为了简化问题便于分析，本文仅将xt，yt设置为随机变量，同时在模型中将市场上的随机冲击归结在一起，假定为白噪声干扰，建立随机动力系统模型来分析市场演化的短期动态和长期均衡。

将公式(7)进行一些简单的整理，加入白噪声干扰后的市场演化模型如下：

(8)

在公式(8)中，rm,α,ex,ey的经济含义同公式(7)，而且为简化问题均假定为常量。将xt，yt分别代表市场中理性交易者和非理性交易者的财富总额，设为随机变量。σx，σy代表两类交易者财富总额的扩散系数，Bit,i=1,2代表相互独立的标准布朗运动。

3 模型分析

以下将对公式(8)所刻画的市场演化动态进行分析，通过对模型的分析，希望解决的几个问题包括：1)模型是否存在全局的和唯一的解；2)作为开放系统的市场演化的长期均衡是什么；3)非理性交易者是否会灭绝，其长期存在的条件是什么。以下将对这几个问题进行分析。

3.1 全局正解的存在性和唯一性

定理1对于任意给定的初值x0,y0，当t≥0 时，公式(8)存在唯一解，而且xt,yt∈+,a.s.。

证明： 由于公式(8)满足线性增长和局部Lipshitz条件，由Oksendal[18]中的定理5.2.1，定理1可直接证得。同时还可得到：

(9)

由上述证明可知，作为开放系统的市场演化模型存在全局唯一解，同时公式(9)还表明，在任意有限时间T内，系统是均方期望有限的。

3.2 系统的长期发展动态

本节将讨论市场长期发展变动的边界问题，分析当时间趋于无穷时，两类交易者财富总额的增长趋势。

为分析方便，定义K=rm+ex+ey，同时定义：V(X(t))=x(t)+y(t) ，使用Ito公式可得：

τk=inf{t∈+;|X(t)|≥k}

取期望，可得：

E(V(X(τk∧T)))=V(X(0))

令t→∞，由于V(X(0))>0，K:=rm+ex+ey>0 ，因此可以得到：

(10)

从而定理2得证，可知当时间趋向于无穷时，公式(8)所表示的系统中两类交易者的财富总额趋向于无穷。

3.3 非理性交易者的长期存在性

本节分析本文探讨的一个核心问题，即非理性交易者的长期存在性问题，本节将证明在一定条件下，当t→∞时，yt→∞。

定义：H=rm-α+ey，由公式(8)中的下式可得：

(11)

定义：

(12)

由于ey>0，而且xt∈+，根据随机比较定理Ikeda和Watanabe[19],Seather等[20]可知：依概率1有yt>ηt，t≥0。

定义g(t,x)=lnx，应用Ito公式可以很容易求出：

(13)

对公式(13)进行分析可以得到以下结果：

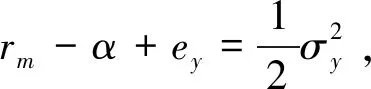
同时由于yt>ηt，a.s.，因而定理3得证。

定理3说明如果非理性交易者的收益率加上净进入率与其收到的扰动相比足够大的话，则非理性交易者可以在市场中长期存在，而且其财富将保持增长直至无穷。反之，如果市场收益率，掠夺率和非理性交易者的净进入率与非理性交易者财富变动的一半方差相比较小的话，非理性交易者也存在灭绝的可能。

3.4 随机演化模型的仿真分析

随机演化动态模型(公式8)的解析解不易求得，因而考虑使用仿真的方法对市场的随机演化动态轨迹进行模拟，同时用多次仿真求样本均值的方法对交易者财富的长期期望进行模拟和分析。下面将使用Higham[21]提出的方法对公式(8)进行仿真。

3.4.1 随机演化动态的样本轨迹

首先使用Higham的方法对公式(8)进行离散化处理，得

(14)

其中ε1t,ε2t是服从标准正态分布的随机变量。

使用公式(14)，设定参数与中国证券市场近20年(1996年1月1日至2016年12月31日)来的收益率和波动性相仿，即设定rm=0.022%，α=0.01%，ex=0.005%，ey=0.02%，ξ0=0.2，η0=0.8，σx=0.01%，σy=0.01%，设定时间周期为8000个交易日，使用Matlab仿真得到的结果如下图1所示：

图1 市场随机演化动态样本轨迹

图中下面的曲线代表理性交易者的财富总额，上面的曲线代表非理性交易者的财富总额。从图1中可以清晰的看到，在市场处于正常的增长过程中时，随着时间增长，理性交易者和非理性交易者的财富都呈现出增长的态势，而且理性交易者财富的增长更加迅速。经过8000个交易日的演化，理性交易者的财富占市场总财富的比例由20%上升到50%。

3.4.2 随机演化动态的长期均衡

Higham[21]同时提出了随机动态系统求期望值的方法，即对系统进行多次仿真，对仿真得出的样本取均值来估计变量的期望值。按照该方法，对公式(14)进行100次仿真(限于计算机性能，100次仿真需运行5个小时左右，因而无法大幅增加样本数来减少样本均值与期望值之间的误差)后求出ξt和ηt，随后求出ηt所代表的非理性交易者占市场财富总额的比例，其变动轨迹如下图所示：

图2 非理性交易者市场份额变动轨迹

从图2中可以看到，在财富方差变动不太大的情况下，市场演化动态中的非理性交易者在市场中所占比例随时间递减，但递减的幅度逐渐减少。与确定性模型相仿，随机模型中非理性交易者所占的比例从长期看会收敛到一个非零的长期均衡值上。

3.5 模型的扩展

目前诸多研究成果表明，市场参与者存在着不同的理性层次和行为特征，如损失厌恶、心理账户等等，仅用理性交易者和非理性交易者来刻画市场参与者不足以充分地表述市场特征，因而考虑将模型扩展为多变量随机微分方程组，通过研究上述模型，能够更为真实细致地描述市场演化动态的轨迹和特征。

假定市场中存在着包括理性交易者在内的n种不同类型交易者，每种交易者的收益率分别为ri,i=1,2,…,n，每种交易者的净进入率为ei,i=1,2,…,n。为简化问题，仍然采用了各类交易者匀质分布、线性进入的假定，即任意时刻t，每一类交易者进入市场的比例均假定为市场交易者总体财富的一个固定比例。

在以上假定下，公式(8)可以扩展为如下的向量形式：

dX(t)=AijX(t)dt+σiX(t)dBi(t)

(15)

其中：

σi,i=1,2,…,n代表各类交易者财富变动的方差，Bit是互相独立的标准布朗运动，对公式(15)进行一些基本的分析可以得到以下结果：

①由于满足线性增长和局部Lipshitz条件，公式(15)所表示的系统存在全局唯一解。

③任意一种交易者的生存和灭绝取决于其收益率及其所受扰动的大小，只要其收益率加上其净进入率相对于其财富波动足够大，该类交易者就不会灭绝。

4 结语

(1)作为开放系统的随机市场演化模型存在全局唯一的正解，而且在有限时间内，交易者财富的总额是均方期望有限的。

(2)市场中两类交易者的财富总额的期望值呈现指数增长的趋势，当时间趋于无穷时，两类交易者的财富总额趋于无穷。

(3)当有新进入者存在时，即便理性交易者的收益高于非理性交易者，市场的长期演化不一定能够消除非理性交易者，非理性交易者的长期存在性取决于其长期收益率和其财富的波动率。

在本文中，为了简化问题，将市场收益率等设为常数参数，将所有的随机因素归结在一起作为白噪声干扰纳入模型中进行分析，而事实上市场演化动态受到一个显著的主要因素的干扰和其它一些次要因素的干扰。交易者的收益率是一个显著的主要因素，将其作为一个Markov过程纳入模型，将模型扩展为有Markov冲击的市场演化模型可能会得到更多更好的结果。