空心线圈模拟积分器时间常数定量分析

马玉龙 ，夏雨 ，2，宋斌 ，2，沈志浩 ，王海全

（1.国电南瑞科技股份有限公司，江苏 南京 210061；2.智能电网保护和运行控制国家重点实验室，江苏 南京 210061）

0 引言

保护用电子式电流互感器（以下简称ECT）通常采用空心线圈作为一次传感单元，克服了传统电磁式互感器磁心饱和，铁磁谐振等问题［1］，能够以较大频宽对一次侧大范围变化的电流进行高准确度测量，在电力系统故障情况下的瞬态大电流检测领域备受关注，目前已经在智能化变电站中得到应用。空心线圈和积分器组成的测量系统不仅在稳态电流的测量上具有很高的准确度，还能还原故障暂态电流。对应一次故障暂态电流，瞬时电流大，电流成分中不仅包括周期分量，还包含非周期分量，如何将故障暂态电流测量误差降低到允许范围内，是空心线圈和积分器组成的测量系统的设计难点。

大量的文献［2-4］对有源积分器的设计进行了研究，或者从稳态角度进行分析，或者从暂态角度将被测电流的周期分量和非周期分量分开分析，或者定性地给出电路参数的选择方法，而保护用电子式电流互感器测量系统暂态运行时瞬时误差不仅仅与非周期分量有关，还与发生故障时的周期分量有关，同时对参数选定的积分器，暂态运行时的瞬时误差限值还受到一次回路时间常数的限制，必须指定相应的适用范围，这就存在积分器参数如何定量设计的问题。针对上述问题，从有源积分器入手，以满足GB/T 20840.8—2007［5］要求的暂态保护电子式互感器5P及5TPE级准确度要求为目标，详细分析影响积分器性能的各种因素，给出模拟积分器积分时间常数定量选取方法。

1 有源积分器

1.1 采集系统建模

空心线圈自身参数对数据采集精度的影响可以忽略不计［3］，由空心线圈与积分器构成的空心线圈采集系统等效电路如图1所示。积分器采用有源积分器，R1为积分电阻，C为积分电容，RP为平衡电阻，R2为反馈电阻。

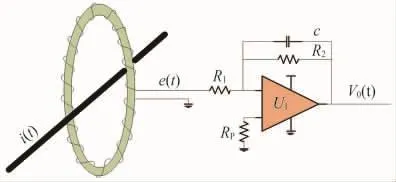
图1 空心线圈采集系统等效电路

一次传感器中的电流i（t）通过空心线圈微分后感应出电压 e（t），e（t）经过积分器，得到输出电压V0（t）。 利用 V0（t）还原得到的电流为 i0（t），i0（t）与i（t）之间的误差就是 i（t）经过图 1 所示采集系统引起的测量误差。i0（t）的时域表达式可表述为

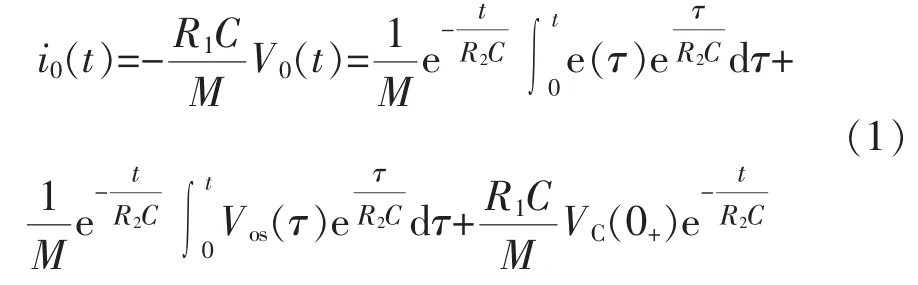
式中：M为空心线圈常数；Vos为输入端的失调电压，由运算放大器电压U1计及各种失调因素后计算而得；VC（0+）为零时刻积分电容上的初始电压；τ为时间t的自变量。

1.2 采集系统误差影响因素分析

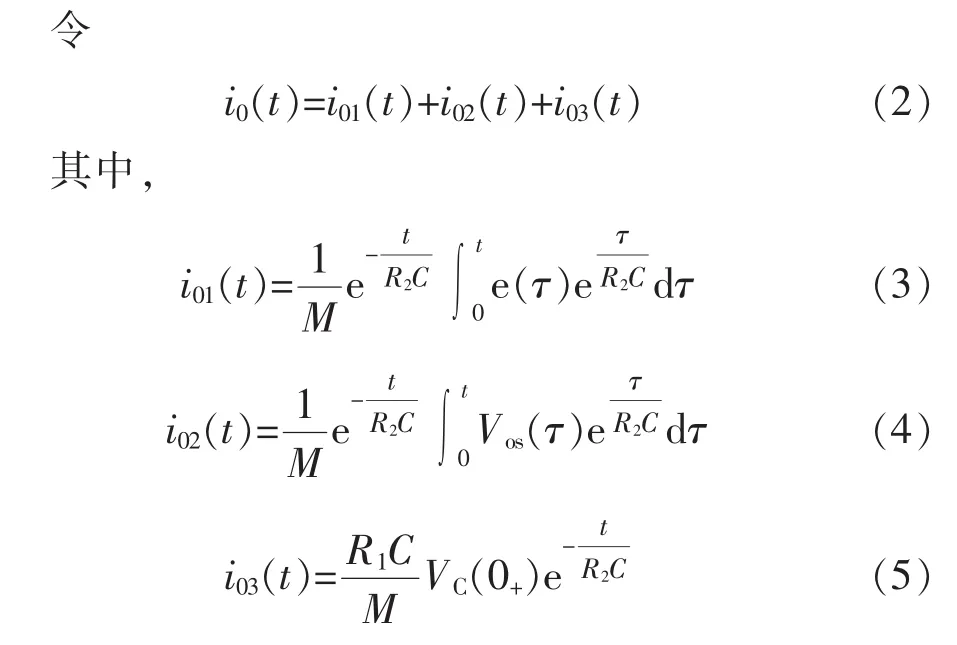
式中：i01（t）为不考虑有源积分器使用运放和积分电容带来的影响的情况下，一次电流经过图1所示测量系统还原得到的电流；i02（t）为运放自身积分漂移量对积分输出的影响；i03（t）为零时刻积分电容的初始电压对积分输出的影响。不考虑模拟器件噪声带来的影响， i01（t），i02（t）， i03（t）包含了所有积分器还原电流值 i0（t）的影响因素。

对于不同的一次电流 i（t）， i02（t）和 i03（t）带来的影响都是一样的，上电阶段均表现为指数型衰减直流分量，衰减的时间常数均为R2C，稳定后的值为0。这2项电流只在上电阶段对系统误差有影响，对系统稳态运行和暂态运行影响均可忽略，因此对积分器引起的测量误差，可只考虑 i01（t）。

电力系统保护应用既需要考虑稳态运行，又需要考虑暂态运行，且稳态运行的输入误差和暂态运行的瞬时误差的要求不同。本文以i（t）为一次传感器输入电流，i01（t）为经过图1所示测量系统还原得到的电流，分别分析稳态运行误差与暂态运行误差。

2 稳态运行输入误差

电力系统保护中衡量电流稳态运行的输入误差，需要同时考虑幅值误差和相角误差。

设一次系统稳态运行时的输入交流信号［6］为

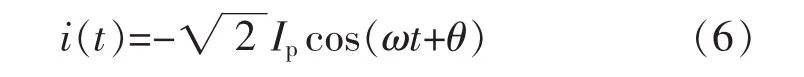
式中：Ip，ω，θ分别为一次系统稳态输入交流电流的有效值、角速度和初始相位。

利用积分器输出还原得到的i01（t）为

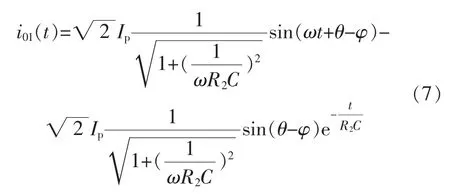
式中：φ=arctan（ωR2C），为积分器引入的相角误差。

i01（t）有2项：前一项为积分初值引起的直流分量，可以通过消去法去除，稳态分析可不考虑；后一项需要限制在5TPE级规定的稳态运行时幅值误差限值1%和相角误差限值1°内，即：

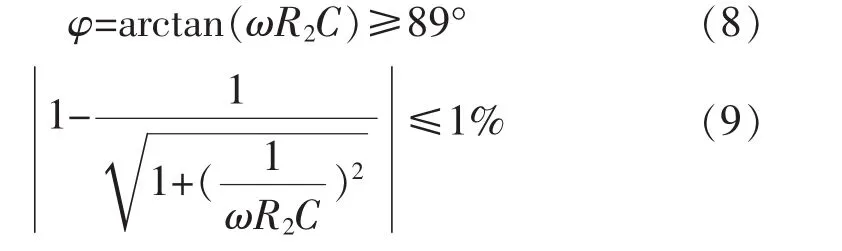
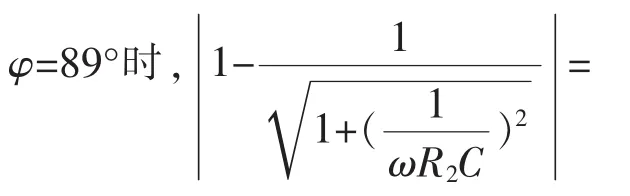
3 暂态运行的瞬时误差

电力系统发生短路故障时，从短路发生到故障切除，这期间会经历一个暂态过程。当系统发生三相短路时，一次短路电流的瞬时值的近似表达式［5］为

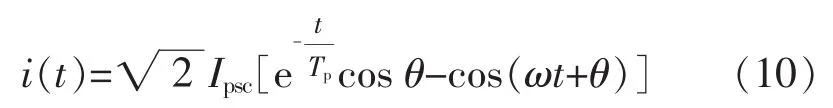
式中：Tp为一次时间常数，由短路位置决定［5］；Ipsc为一次短路电流的有效值。

考虑最严重的短路情况［5-6］，即 θ=0°，短路电流的瞬时表达式为

式中：is1（t） 为短路电流的非周期分量；is2（t）为周期分量。

利用积分器输出还原得到的i01（t）为

式中：i01-1（t）和i01-2（t）分别为积分器输出还原得到电流值的非周期分量和周期分量。

5TPE级对瞬时误差的定义为在准确限值条件、额定一次时间常数和额定工作循环下的最大峰值瞬时误差为10%。峰值瞬时误差同时包含暂态直流分量误差和暂态交流分量误差。一次电流最大峰值瞬时误差定义范围为额定扩大一次电流到暂态特性的额定一次短路电流，其中额定扩大一次电流不小于额定一次电流。为分析方便，额定扩大一次电流按额定一次电流取值。测量系统的最大瞬时相对误差为

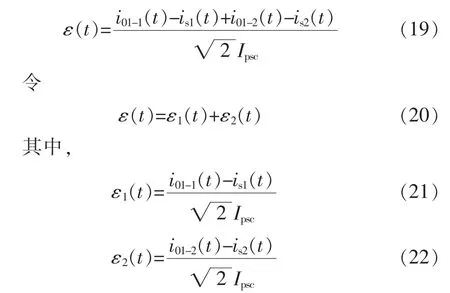
式中：ε1（t）和 ε2（t）分别为 i01（t）中周期分量和非周期分量的瞬时相对误差。

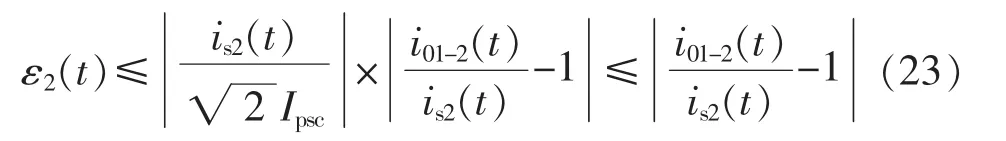
将式（14）和式（18）代入式（23），可得：

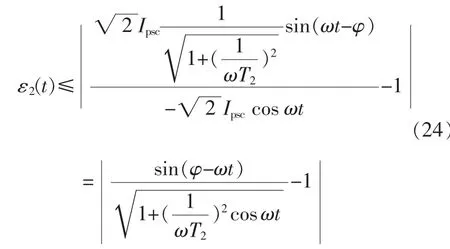
暂态运行误差分析需在系统满足稳态运行误差要求的基础上进行分析，按照稳态分析要求，需要T2大于 0.18 s。 此时，89°≤φ≤90°，

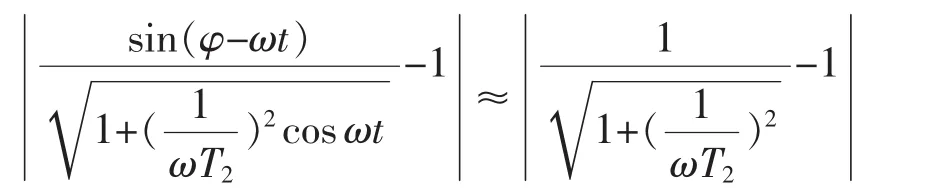
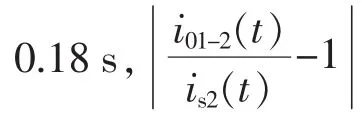
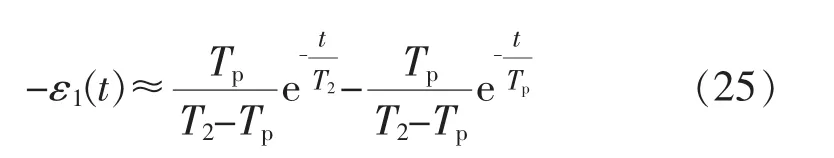
对 ε1（t）求导，获取其单调性

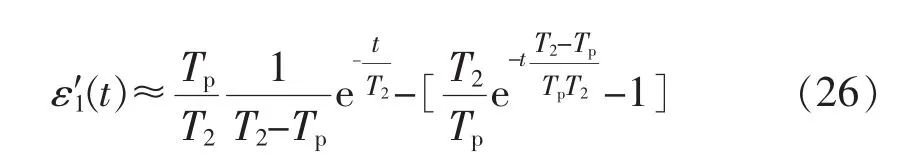
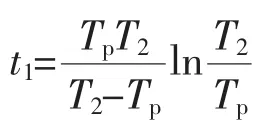
4 实验测试与分析

为验证理论分析的正确性，在实验室搭建测试系统。测试系统由电流源、空心线圈、积分远端模块和激光供能合并单元组成，测试系统等效电路如图2所示。电流源输出测试电流通过空心线圈，空心线圈输出的感应电压送入积分远端模块，积分远端模块使用激光供能合并单元供电。电流源为OMICRON CMC356，自带多个高精度采样通道，采样频率高达28.44 kHz，能够可靠还原工频信号。

测试过程中，OMICRON采集电流源输出电流在采样电阻上的电压VP、空心线圈输出电压V1和积分器输出电压V2，采集到的数据送入带测量误差分析软件的计算机后，利用Matlab计算测量误差。空心线圈变比为600 A/150 mV。在实验室通过“等安匝”的方法施加一次电流，空心线圈一次均匀绕制400匝，在电流源输出1.5 A时，空心线圈输出150 mV。积分远端模块上设计本文论述的有源积分器，时间常数T2在测试过程中通过改变阻容值改变大小。

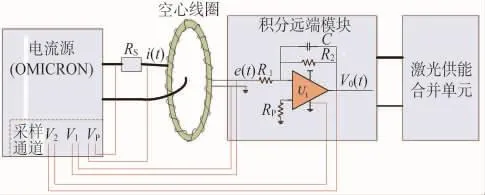
图2 测试系统等效电路

测试系统中空心线圈性能测试结果如表1所示，额定电流为600 A，输入100%额定电流时，幅值误差为0.4%，输入200%额定电流时，幅值误差为0.01%，2种情况下的角差在0.05°内。下面的测试过程中，分析软件对幅值进行校正，使得空心线圈输入100%额定电流时，空心线圈的输出误差小于0.05%。

表1 空心线圈性能测试结果

对220 kV及以下电力系统，或GB/T 20840.8—2007［5］提到的短路发生在数公里外的应用场合，一次时间常数一般在60 ms以下，而对于500 kV及以上的电力系统一次时间常数会达到200 ms以上。测试过程中，一次时间常数Tp选择60 ms，100 ms和200 ms共3个参数，积分器时间常数T2选择500 ms和1 000 ms共2个参数，组合进行测试电流源分别输出0.50 A和0.75 A，进行稳态运行和暂态运行测试。

稳态运行测试结果如表2所示，测试结果证实了T2＞0.18 s时，幅值和相位误差均能限制在5TPE级规定的幅值误差限值1%和相角误差限值1°内。

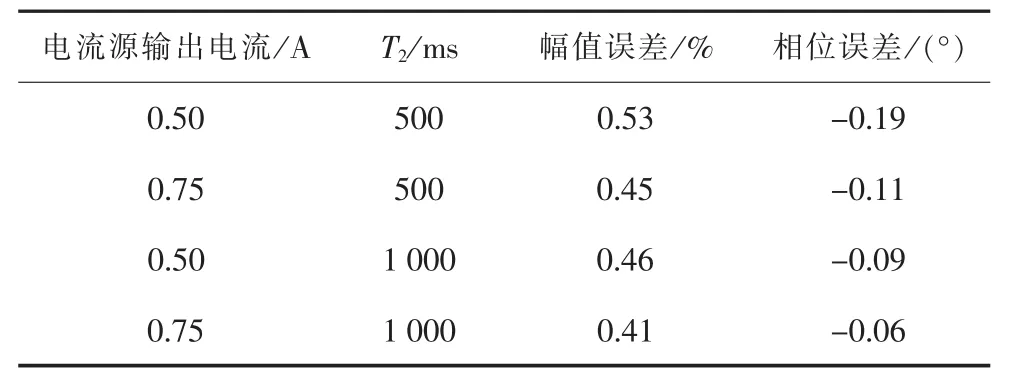
表2 稳态运行时的输入误差

暂态运行时的测试结果如表3所示。测试结果表明：按照T2>8.3Tp设计积分器参数，最大峰值瞬时误差能控制在10%范围内；T2≤8.3Tp时，最大峰值瞬时误差大于10%，不能满足要求。

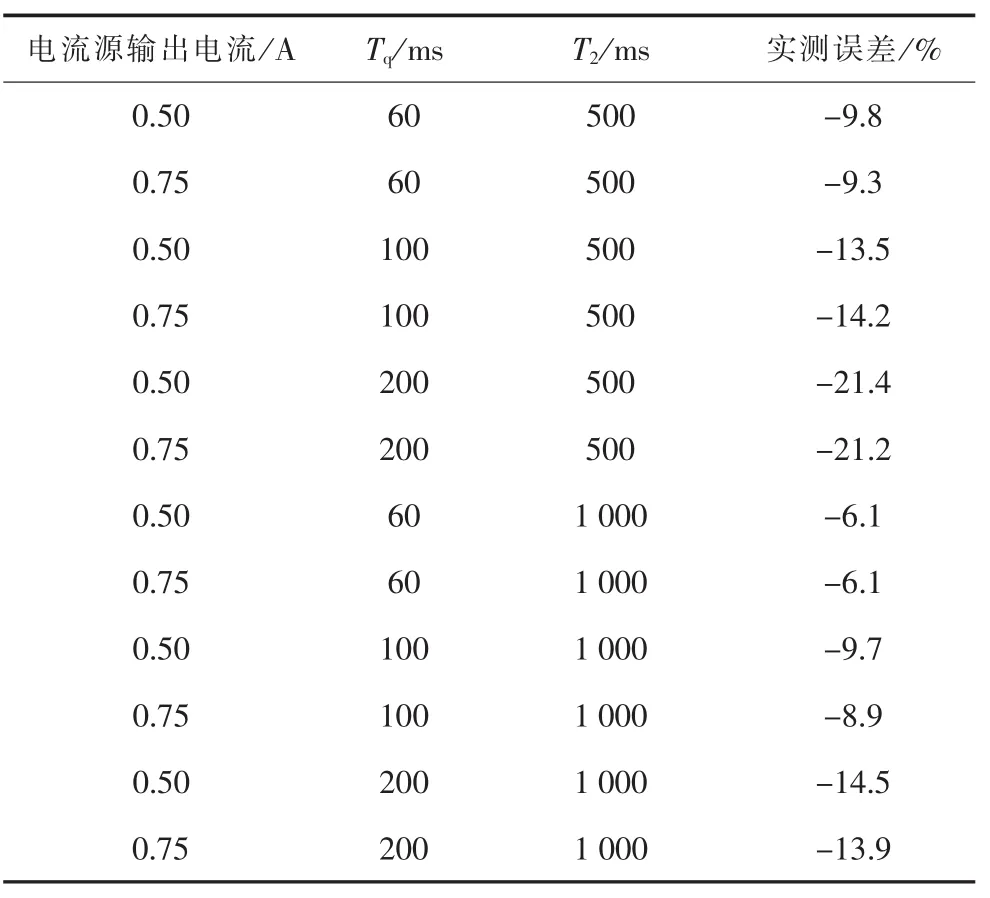
表3 暂态运行时的最大峰值瞬时误差

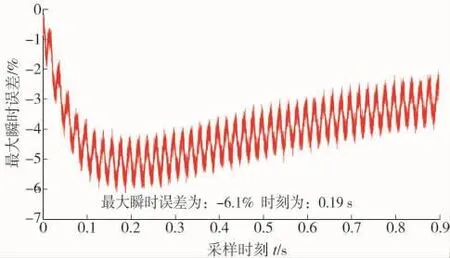
图3 最大峰值瞬时误差实测波形

图3为取T2=1 s，Tp=60 ms时，使用一组录波数据计算得到的最大峰值瞬时误差波形。最大峰值瞬时误差大小和发生时刻与本文理论分析相符。

5 结语

空心线圈测量系统的暂态运行时的瞬时误差与发生故障时的周期分量和非周期分量有关，而且非周期分量对最大峰值误差的贡献远大于周期分量。

在相同一次时间常数下，积分器时间常数越大，暂态运行时的最大峰值瞬时误差越小。

空心线圈测量系统暂态运行的瞬时误差与一次时间常数有关。积分器参数选定的保护电流互感器，只能在故障电流一次时间常数小于一定限值的条件下，才能满足5TPE级的暂态准确度要求。所以保护用电流电子式互感器的选用必须要对其应用条件进行确认。

定量给出模拟积分器积分时间常数设计规则，该规则可直接用于电路设计，也可作为分析使用模拟积分器的电子式互感器工程现场测量误差的手算方法。