颗粒离散元数值模拟中的宏细观接触力计算方法

2019-06-03关岩鹏张玉芳刘晓丽王恩志

铁道建筑 2019年5期

关岩鹏，张玉芳，刘晓丽，王恩志

(1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084)

颗粒离散单元模拟是一种新兴的模拟岩石或土的力学行为的方法[1]。一些学者使用这种方法来模拟岩土工程问题并取得了一定的成果[2-5]。目前，对于颗粒离散单元法的数值模拟结果的分析大部分停留在被模拟物体非量化的宏观形态上[6-7]，如裂纹的扩展程度、颗粒的堆积形态等[8-9]。对颗粒离散元法数值模拟结果的可量化结果的分析很少有报道。

基于颗粒材料的几何特性，本文采用构造到各个颗粒的切线距离相等的点集的方法，将各个颗粒集合体剖分成一个平面图。然后，利用图论的理论提出了颗粒集合体中宏观和微观接触面的表征方法。在颗粒离散单元数值模拟中，利用此表征方法，提出通过计算权重矢量获得颗粒离散单元数值模拟结果中的宏细观接触力的方法。以边坡工程为算例，计算了土条边界的接触力，计算结果与理论计算结果有较好的一致性，且本文计算结果更能体现岩土体接触力分布离散的特点。

1 构造辅助平面

对于2个相接触的颗粒，构造到2个颗粒的切线长度相等的点集[10]，经过计算发现此点集为一条直线(如图 1所示)，这条直线恰好通过2个颗粒的接触点。如果2个颗粒不接触则该点集仍然是直线并且穿过2个颗粒之间的间隙。对于由若干个圆形颗粒构成的颗粒集合体，构造到各个颗粒的切线长度相等的点集，可以形成一个由直线构成的平面图，如图1中的直线所示[11-12]。其中，实线表示到相互接触的2个颗粒切线长度相等的点集;虚线表示不相互接触的2个相近颗粒切线长度相等的点集。

图1 利用本文方法构造的辅助平面

2 接触力计算方法

2.1 细观接触

将由上述方法构成的平面图中各直线的交点定义为一个“节点”，将这些直线(“节点”的连线)定义为“边”。每一个节点表示一个孔隙，用vi表示。每一条边表示2个颗粒间的接触面，用e=(vi,vj)表示。

2.2 宏观接触面

宏观接触可以用图论中的“路”来表示，“路”是由一系列相互连接的节点和边组成。表达式如下

p=[vi,(vi,vj),vj(vj,vk),vk,…,vl(vl,vn)，…，vn]

(1)

式中：p为图论中的“路”;vi,vj,vk,…,vl,vn是各不相同的节点。

用图论理论中的“路”表示的的宏观接触面如图2所示。

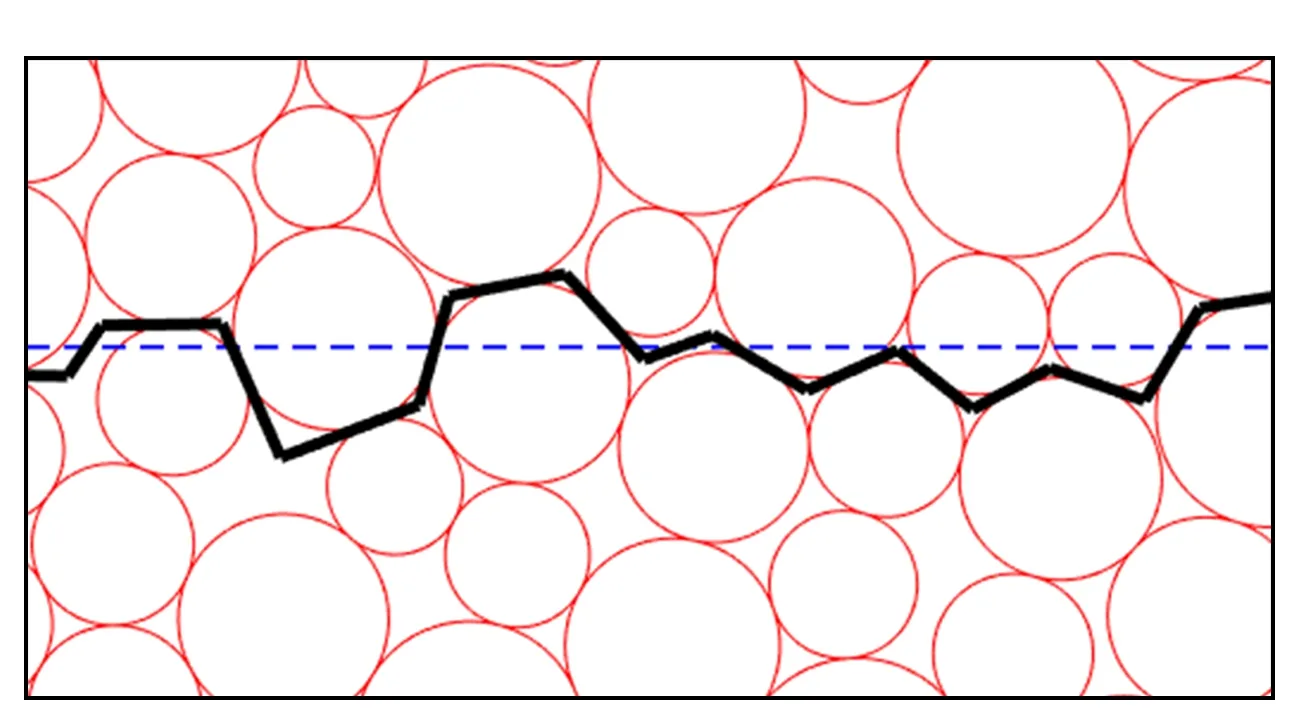
图2 宏观接触面

2.3 宏观接触力的计算方法

如上节所述，用一个构造平面图的边e表示颗粒集合体的2个颗粒间的接触。为每一个边e设置一个权重w(e)，w(e)的值为e表示的接触处的接触力。定义P为颗粒集合体中的某个宏观接触。定义W(P)为此宏观接触上的接触力。由于力是矢量，可以通过矢量相加方法进行求和，所以W(P)的计算方法为对w(e)进行矢量求和运算，表示为

W(P)=∑w(e)e∈p

(2)

3 算例

3.1 计算方法

对于边坡工程，部分学者采用颗粒离散单元法进行了数值模拟，取得了一定的成果，但大多是对边坡破坏后的堆积形态的描述，求解宏观量化结果的较少。本节通过以边坡颗粒离散单元的数值模拟结果中的接触力计算值与理论计算值作对比，论述本计算方法的优缺点。

滑动面的路径如图3所示。对边坡进行理论稳定性计算，常用方法为条分法，即假设边坡为刚体，设定一个潜在滑动面和土条边界进行计算分析。对于由颗粒堆积成的边坡，潜在的滑动面上的接触力可用本文提出的宏观接触力的计算方法进行计算。

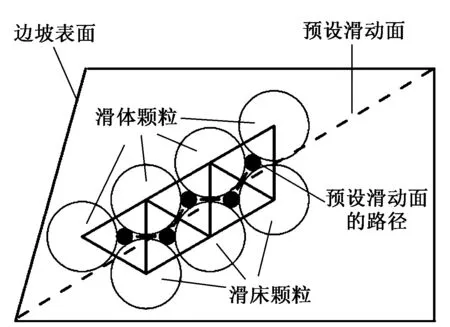
图3 滑动面的路径示意

运用Particle Flow Code计算软件并利用颗粒离散单元方法中的随机填充方法构造了一个简单的斜坡，坡体高度约为6 m，坡面倾角约为60°，如图4所示。

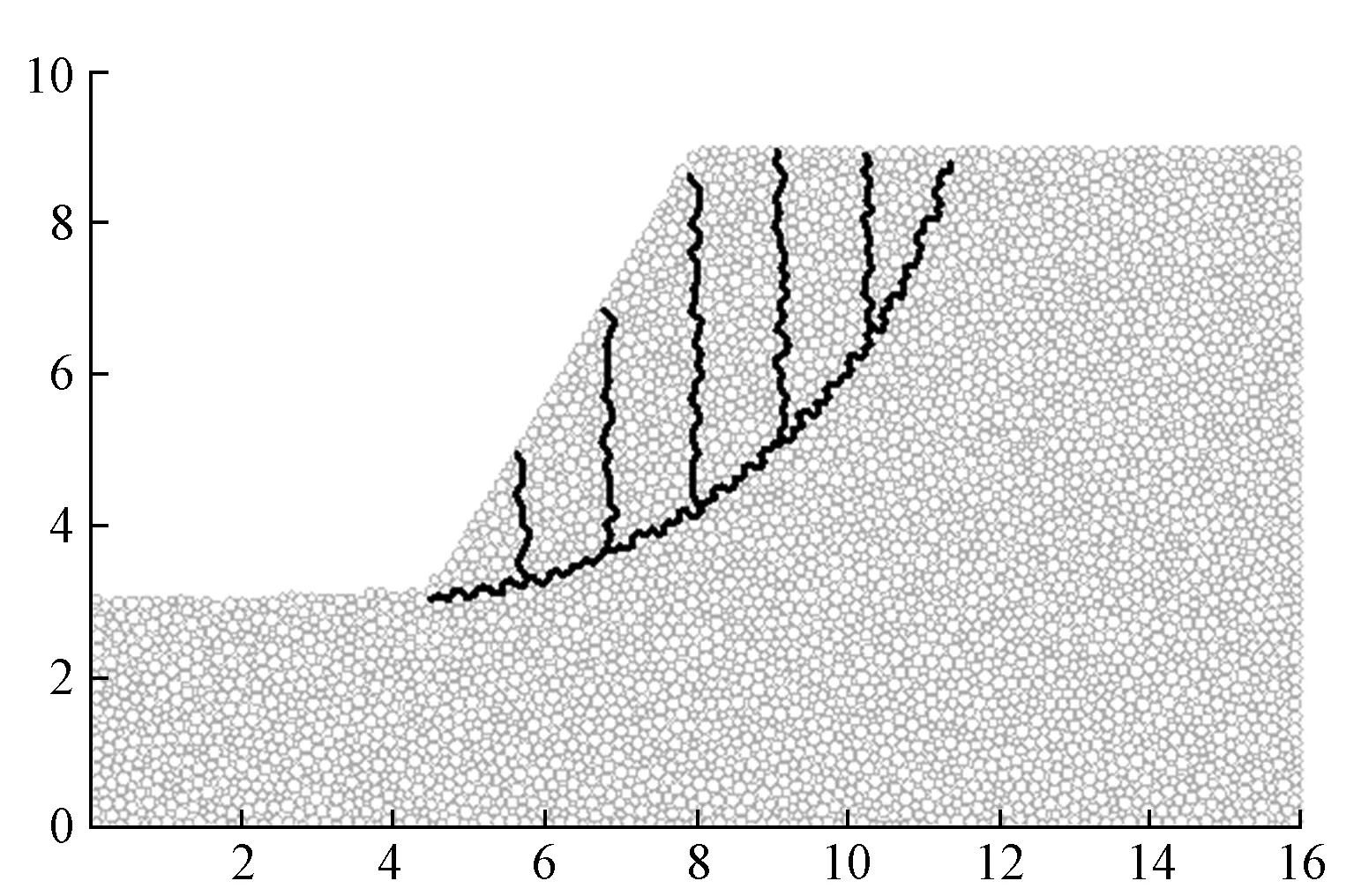
图4 算例模型(单位：m)

算例的宏观参数为：重度取18.5 kN/m3；黏聚力取20 kPa；内摩擦角取15 °；弹性模量取20 MPa；泊松比取0.2。

算例的细观参数[13]为:颗粒密度取2170 kg/m3；颗粒半径取0.05～0.10 m；法向接触刚度取6 kPa；切向接触刚度取6 kPa；法向接触强度取2.0 × 107N/m；切向接触强度取0.4 × 107N/m；颗粒间摩擦因数取0.1。

3.2 接触力求解

一般边坡稳定性的计算方法是预设圆弧形滑动面进行搜索计算，为了与理论法进行对比，本文预设了一个圆形滑动面。利用本文提出的接触面表征方法计算的预设滑动面，如图4中边坡中最下部的折线所示。由于颗粒集合体有别于一般的均质体，具有一定的离散性和不均匀性，所以计算出的滑动面是折线面。

说起地雷，进攻金兰防线的鬼子可是吃足了苦头，许多年后，第七十师团长内田孝行回忆往事曾这样哀叹：“金华、兰溪的阵地上，主要交通线上，埋设了无数地雷，以阻止我军行动，我军因此受到严重损失。”

设定土条宽度为1.0 m，土条间接触力也可以利用本文的计算方法进行计算，如图4中的近竖直折线所示，本文计算了表示土条间接触面的“路”，利用本文方法即可计算出土条间接触力。

简·布法(Janbu法)是条分法的一种，它同时考虑了力矩平衡、土条间法向接触力平衡、土条间切向接触力平衡，而颗粒离散单元法在计算结果稳定后各个颗粒所受到的力与力矩也是平衡的。因此选取简·布法与本文提出的计算方法进行对比分析。

3.3 土条重力

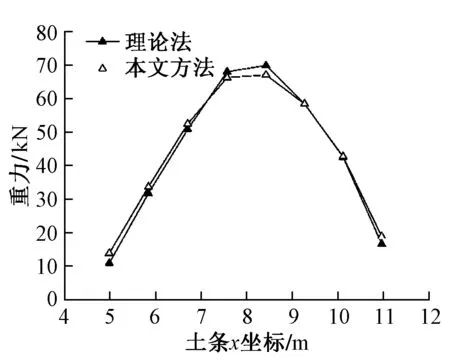
图5 土条重力

颗粒离散单元中，通过计算各个土条内部颗粒的重力来计算各土条的重力，计算结果见图5。由于重力作用，坡体各个位置的密度并不相同，一般坡体下部土体的密度比上部稍大。因此，本接触力计算方法在计算坡体下部的土条重力时，计算结果比理论法大，在其他位置计算的土条上，本计算方法的计算结果偏小，这与此位置的颗粒集合体荷载较小、相对疏松有关。

3.4 切向接触力和法向接触力

本文计算方法及理论法计算结果中，滑动面上的沿滑动方向的切向接触力与垂直于滑动方向的法向接触力计算结果见图6。可知，本文计算坡体下部位置的切向力偏低，这主要是因为理论方法未能考虑部分土条切向接触力可能超过材料强度的情况，本文构建的坡体的稳定性系数约在1.3左右，坡体下部处部分颗粒间的相互作用力已经超过了颗粒间的黏聚强度，导致坡体下部部分土体进入塑性变形阶段，能够承担的切向力变低。

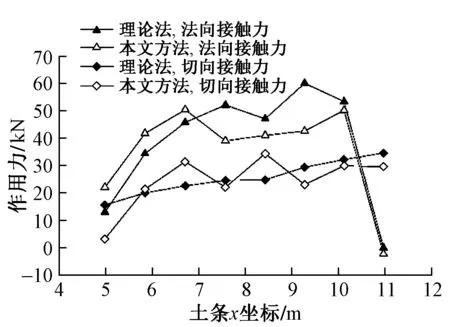
图6 潜在滑动面上的接触力计算结果

在法向接触力方面，本文方法的计算结果在坡体下部位置比理论法高。这主要是因为坡体下部的颗粒被挤密，导致其承受了更高的重力，为了维持平衡，法向力也相应增高。

3.5 条间力

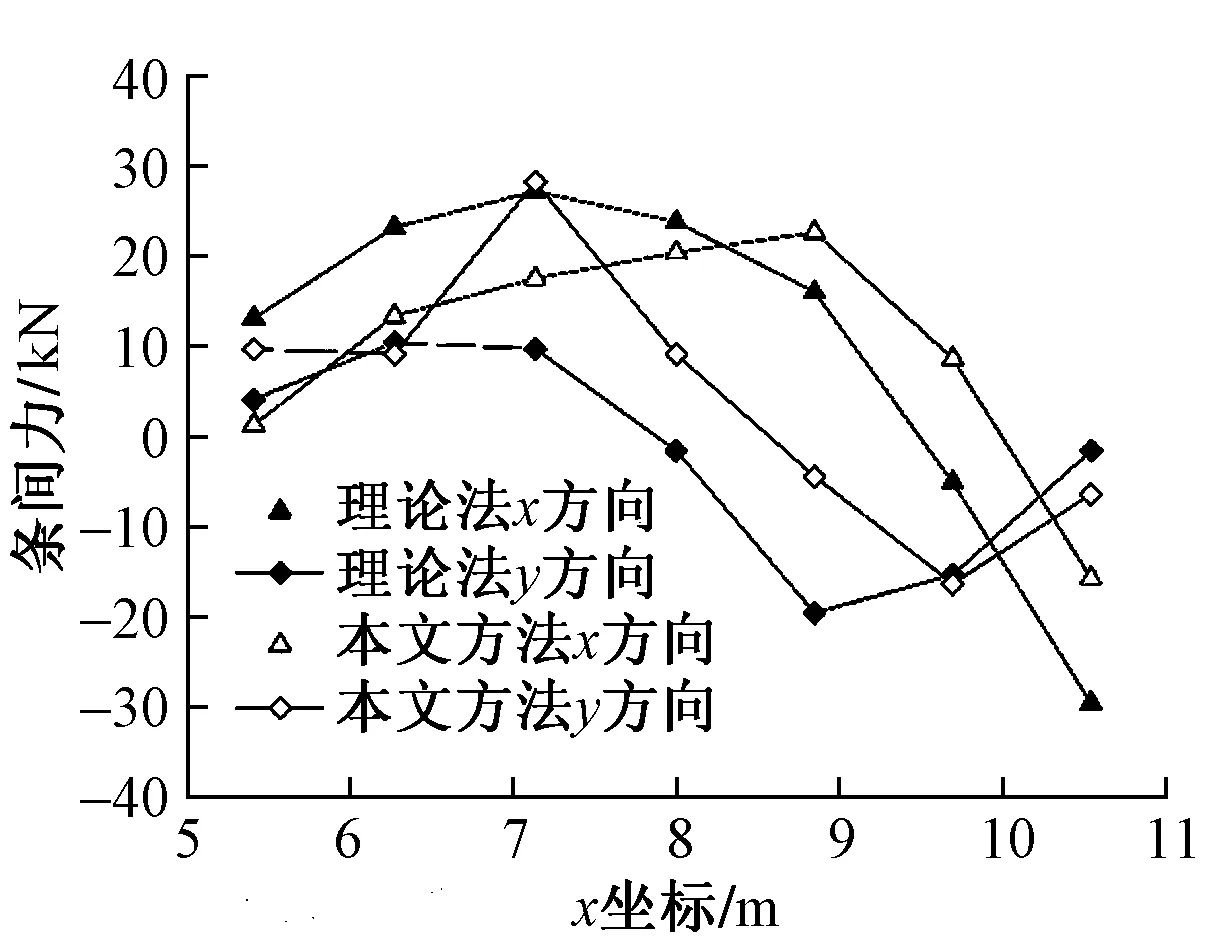
图7 条间力计算结果对比

理论法及本文提出的计算方法计算的各土条间接触力(x方向和y方向)见图7。可知，2种方法计算结果较为相符，部分位置存在一定的差异。由于理论法与本文方法计算的模型均为稳定状态，在力学上维持平衡，那么法向力、切向力的计算结果存在差异必然导致条间力的计算结果存在差异。例如，在坡体最左侧土条上，本文计算结果土条底部法向接触力偏大，相对应的土条间的y向作用力偏大。

可以看出，本文计算方法与理论方法计算结果具有一致性，理论法未能考虑到岩土体是一个弹塑性体，而颗粒离散单元法考虑了岩土体的弹塑性、非连续性等特点，计算结果更准确。