U肋加劲板受压力学性能分析

赵 秋，张骏超，翟战胜，聂 宇

(1.福州大学 土木工程学院，福建 福州 350108；2.湖州市交通规划设计院，浙江 湖州 313000)

对于较长跨径的斜拉桥或悬索桥而言，其主梁截面多采用抗扭刚度大、横向抗弯刚度大的钢箱梁。而在钢箱梁顶底板处又经常设置U形加劲肋以避免发生屈曲破坏。早期关于加劲板稳定性问题的研究大多以弹性理论为基础。Chou等[1]以旧金山—奥克兰海湾大桥为背景，对U肋加劲板的设计强度进行了检验，试件先发生整体失稳，而后发生加劲板与U肋局部失稳破坏；姚行友、陈均霞等[2-3]对加劲肋的稳定理论进行了研究。但是我国钢箱梁的建设起步较晚且研究较少，而U肋加劲板又是主要的受力构件，所以有必要对U肋加劲板各组成子板件的屈曲性能进行研究。

本文探讨U肋加劲板受压稳定的数值模拟方法，并将模拟结果与U肋加劲板受压稳定承载力试验结果进行对比。该成果可为混合钢U肋加劲板的受压性能研究提供分析手段，以减少试验成本。

1 试件设计

在钢箱梁的顶板或底板沿横桥向选取含有3个U肋的加劲板、纵桥向选取两横隔板间距范围内的U肋加劲板作为本文混合钢U肋加劲板研究对象[4-6]。通过改变加劲板的几何尺寸与母板-U肋的钢材强度组合，共设计3组9块混合钢U肋加劲板试件[7]，以探究混合钢U肋加劲板在轴压状态下的极限稳定承载力。根据试验设备能力，试验试件按1∶2.5缩尺，试件横截面如图1所示，相关参数见表1。

图1 试件横截面

试件编号母板强度/MPaU肋强度/MPa母板板厚tm/mmU肋板厚tu/mmU肋上缘宽bs/mmU肋下缘宽bx/mmU肋高度h/mmHj1-13452358474120100Hj1-234523510464120120Hj1-334523584104160100Hj2-12353458474120100Hj2-223534510464120120Hj2-323534584104160100Hj3-13453458474120100Hj3-234534510464120120Hj3-334534584104160100

注： 试件高度均为1 600 mm。

图2 加载装置

为了模拟两端铰接的轴心受压试件，加载装置设有转动装置，如图2所示。转动装置由圆钢棒和2个卡槽组成，卡槽可限制住钢棒的水平位移，使钢棒只能转动。采用分级单调加载的方式，加载初期每级加载递增量约为100 kN，当总荷载大于估算极限荷载的50%时采用位移加载，逐步达到极限荷载。

2 数值模拟影响因素分析

2.1 有限元模型

建模时采用可以考虑大变形和材料非线性的Shell 181壳单元，弹性模量为2.06×105MPa。为了防止端板变形，端板刚度扩大104倍，然后分析不同边界条件对试件稳定的影响。根据试件的规格建立有限元模型，如图3所示。

图3 有限元模型

2.2 边界条件

加劲板作为扁平钢箱梁的顶底板，受横隔板和两边侧腹板的约束，相当于四边简支板。由于扁平钢箱梁中腹板间距比横隔板间距大，两侧腹板对加劲板的约束作用变得不明显，因此可以把加劲板的边界条件简化为两边简支[8]。为了模拟试件两边简支受力，在试件两端设置了转动装置。但在试验过程中转动装置并非为理想的铰，且有时会出现失效现象。因此对试件受压机理和承载力分析时，有必要考虑转动装置受到约束和转动装置没有受到约束2种边界情况。

图4 试件稳定系数位移曲线

由图4可知：①在转动受到限制的情况下，试件的稳定系数峰值较转动自由情况下峰值有不同程度的增大，试件Hj1-1增大了24.5%，试件Hj2-1增大了11.0%，试件Hj3-1增大了3.4%。②由试验得到的试件稳定系数峰值略大于转动自由情况下的峰值，其中试件Hj1-1增大了7.5%，试件Hj2-1与Hj3-1的试验值峰值与转动自由情况下的峰值基本相同，说明转动自由度对试件的影响较大，且上述转动自由的边界条件与试验结果吻合较好。③试件Hj1-1和Hj3-1的破坏模式与有限元模型的边界条件设置相关。当转动自由时，试件Hj1-1和Hj3-1表现为明显的失稳破坏，而试件Hj2-1的破坏模式并没有改变，具有强度破坏或整体失稳的性质；试件Hj1-1的破坏模式与试验结果相吻合，而试件Hj2-1与Hj3-1的破坏模式与试验结果不同，说明这2个试件的转动受到一定的限制。

试件破坏时Mises应力分布见图5，图中达到屈服强度的区域标识为红色。可知，对于同一个试件，转动装置受限与否会影响试件的破坏模式，从而导致承载力的变化。结合图4可知，采用转动自由的边界条件更加接近试验情况，因此本文采用此种边界条件。

图5 试件破坏时Mises应力分布

2.3 初始几何缺陷

初始几何缺陷可以分为构件整体几何缺陷、板件局部几何缺陷，以及加载时的偏心效应。在有限元模型中，试件的整体几何缺陷往往以初弯曲的方式计入，通过将模型节点按照正弦半波形式的偏移来实现；对于局部几何缺陷的施加，采用将其第1阶屈曲变形按比例赋予模型中的方式[9-10]。为简化计算材料模型均取理想弹塑性。以每组试件的第1个试件为例来分析初始几何缺陷对试件承载力的影响。

1)整体几何缺陷

整体几何缺陷指的是沿长度方向出现的初始挠度δ，GB 50017—2003《钢结构规范》[11]规定了其与构件长度l比值的上限为δ/l=1/1 000。本文分别取δ/l=1/750,1/1 000，1/1 5 000 分析整体几何缺陷对试件承载力的影响，如图6所示。

图6 稳定系数随整体初始挠度的变化曲线

由图6可知：随着整体初始挠度的增大，试件的稳定系数呈下降趋势，其中试件Hj1-1和Hj2-1下降幅度较大(下降约7%)；Hj3-1下降幅度较小(下降约2.35%)。说明整体几何缺陷幅值对于试件承载力的影响随着混合钢试件不同强度组合而不同，但稳定系数均随整体几何缺陷幅值的增大呈下降趋势。

2)局部几何缺陷

局部几何缺陷是针对构件中板件的缺陷，但具体缺陷分布及幅值的规定存在一定争议。本文采用文献[12]中提出的局部初始挠度曲线沿柱轴向波长为b的观点，以及GB 50018—2002《冷弯薄壁型钢结构设计规范》[13]中δ/b≤0.01的规定。本文分别取δ/b=1/100,1/150,1/200,1/250,1/300，分析局部几何缺陷对试件承载力的影响，见图7。

图7 稳定系数随局部初始挠度的变化曲线

由图7可知，随着试件局部几何缺陷幅值的增大，试件的稳定系数呈下降趋势，但是下降幅度不同。其中试件Hj1-1和Hj2-1下降幅度较大，两试件稳定系数的最大值、最小值之差与最小值相比约为18%。而试件Hj3-1下降幅度较小，稳定系数的最大值、最小值之差与最小值相比约为5%。说明试件的局部几何缺陷幅值对于试件承载力的影响和试件的强度有关，且稳定系数随局部几何缺陷幅值的增大呈下降的趋势。

3)加载偏心分析

加载过程中由于对中不精确，荷载偏离构件截面形心产生偏心效应，这在试验中是无法避免的。对于偏心距的取值，在JTJ 025—86《公路桥涵钢结构及木结构设计规范》[14]中，关于H形和箱形受压细长杆的稳定承载力计算，对初始偏心距e0的规定：e0=0.008h(λ>45)。其中，h为截面高度，λ为试件长细比。在有限元分析中，以是否考虑残余应力将构件分为2组，并将每组中的偏心距范围取-0.003～0.003 m进行稳定承载力分析，得到构件稳定承载力与偏心距之间的关系，如图8所示。

图8 稳定系数与偏心距的关系

由图8可知，3组试件在计入残余应力后的稳定系数比不计入时降低了20%左右，这说明残余应力对构件稳定承载力的影响较大。偏心率对试件稳定系数的影响和偏心的方向有关。对于强度高于U肋强度的被加劲板，偏心方向设置在偏向U肋一侧会导致其稳定系数降低；对于等强度钢U肋加劲板，其偏心的方向要根据试件轴心受压时的失稳破坏方向和偏心距的大小而定，与试件的初始缺陷分布有关；对于强度低于U肋强度的被加劲板，偏心方向设置在偏向被加劲板一侧会导致其稳定系数降低。

2.4 焊接残余应力

残余应力是影响构件稳定承载力的重要因素[15]。当外加荷载和残余压应力叠加达到试件的材料屈服强度时，该截面就失去了承载能力，削弱了试件的有效面积，影响其稳定性。

1)残余应力简化方式

图9 残余应力简化分布形式

本文采用以折代曲的残余应力简化分布形式[16-17]分析试件的残余应力分布规律，见图9。该简化分布的提出过程如下：首先通过盲孔法的残余应力测试试验结果验证有限元数值模拟方法的正确性，再通过数值模拟对不同结构尺寸、不同强度组合混合钢U肋加劲板的焊接残余应力进行参数分析，揭示其残余应力分布规律，最终利用残余应力自平衡原理推导得到。

图9中各参数计算式分别如下

(1)

(2)

(3)

式中：σm,rc，σu,rc分别为母板和U肋的残余压应力；σm,rt，σu,rt分别为母板和U肋的残余拉应力；σm,y,σu,y分别为母板和U肋的屈服强度；σy为钢材的屈服强度；c为U肋翼缘宽度；b为U肋腹板间距；b1为母板残余拉应力分布宽度；h1为U肋残余拉应力分布宽度，p1，p2分别为被加劲板所分配的残余拉、压应力分配比例。具体数值选取，请参考文献[16-17]。

2)残余应力对结构稳定承载力影响

在ANSYS中施加残余应力，应首先编写初始应力文件(IST文件)，在加载的第1步用ISFILE读入这个初始应力文件，即把初始应力作为一种荷载施加在结构上，这样结构中就存在初始应力(残余应力)，然后进行承载力分析。为更好地模拟焊件的残余应力并考虑模型的计算效率，在焊缝位置附近单元网格划分密一些，远离焊缝的单元网格划分粗一些。以试件Hj1-1 为例，纵向焊接残余应力分布如图10所示。

图10 纵向焊接残余应力分布(单位：kPa)

图11 不同残余应力分布下试件的稳定系数纵向位移曲线

3 试验验证

有限元模型采用可以考虑大变形和材料非线性的Shell 181壳单元，采用分级单调加载方式，应用弧长法进行求解。由于材料拉伸试验结果并不呈现理想弹塑性，因此，在有限元材料模型中以拉伸试验结果为基础，并采用多线性随动强化模型对表1中所有试件的结果进行对比验证，以获得与试验更加接近的效果。

3.1 试验破坏模式验证

图12 不同试件试验破坏模式与有限元破坏模式对比

试件在不同破坏模式下的承载力有所不同，因此，可以通过对比试验破坏模式与有限元破坏模式来判定有限元分析的准确性。不同试件试验破坏模式与有限元破坏模式对比如图12所示。可知，试件Hj1-1,Hj2-1,Hj3-1在试验与有限元模拟中均发生了U肋的局部屈曲，但二者发生局部屈曲的位置并不相同：有限元模拟中的局部屈曲多发生在试件跨中位置，而试验中的局部屈曲位置不固定，多发生在距离U肋顶、底端l/3截面处，这与试件实际缺陷的位置分布有关。对于试件Hj3-1,Hj2-2和Hj2-3来说，试验和有限元模拟均发生了整体弯曲，破坏模式基本一致。而试件Hj2-1,Hj1-3和Hj3-3由于转动受到约束导致U肋端部或根部发生屈曲，因此不作对比。

3.2 试件稳定系数与位移曲线验证

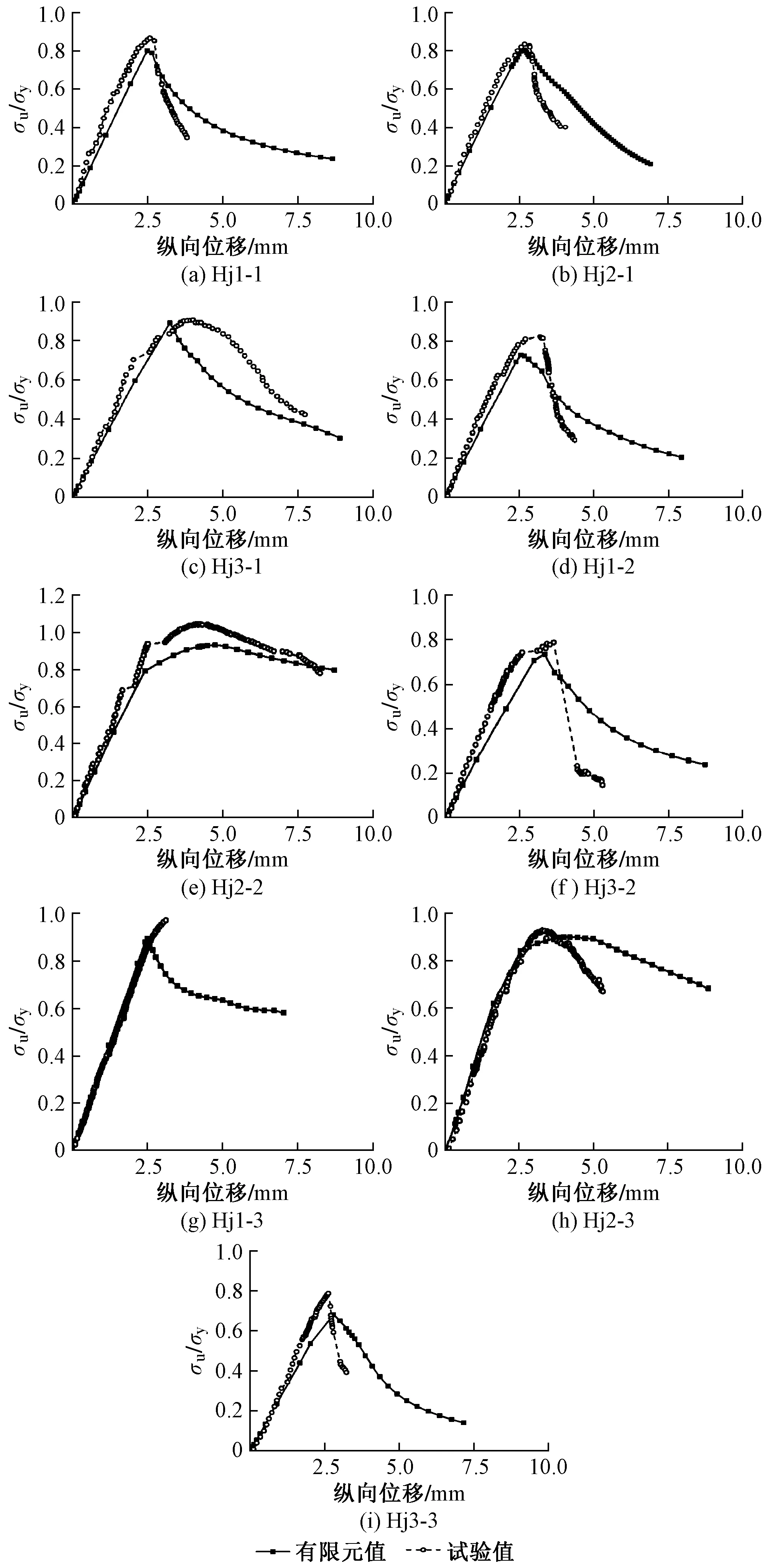
图13 不同试件稳定系数位移曲线

4 结论

1)试件两端转动约束是否被限制将导致试件的破坏模式和承载力发生改变。在有限元模型中，试件一端约束形心轴Uy,Uz两个方向的位移，一端约束形心轴Ux,Uy和Uz三个方向的位移，可以正确模拟试件的边界条件。

2)当加载偏心产生的弯矩效应与轴心受压试件整体弯曲破坏方向一致时，试件的稳定承载力会随着偏心距的增大而减小；当加载偏心产生的弯矩效应和轴心受压试件整体弯曲破坏方向不同时，试件的稳定承载力会随着偏心距的增大而增大。

3)混合钢U肋加劲板试件的稳定系数随整体几何缺陷和局部几何缺陷幅值的增大而减小，但减小的程度和构件强度组合有关。

4)局部几何缺陷取板宽的1/200，整体几何缺陷取试件长度的 1/1 000，加载偏心距取截面高度的0.02倍，可以较好地模拟混合钢U肋加劲板的初始几何缺陷。