密立根油滴实验的数据处理方法研究

袁哲诚，王宽亮，陆李威，徐哲真，许 飞，罗锻斌

(华东理工大学 理学院 物理系，上海 200237)

美国物理学家密立根利用自己设计制作的仪器，通过对带电微小油滴电量的准确测量，证实了油滴电荷量的不连续性，即所有电荷量均为元电荷的整数倍，同时通过实验确定了元电荷的量值. 密立根在油滴实验中采用宏观的力学模式(油滴的受力分析)来研究微观世界的量子特性(电荷的不连续性)，相关物理量的数量级跨度达到1020，数据的精确与结果的稳定令人震撼. 密立根油滴实验中所包含的实验构思与实验技巧，也堪称近代物理实验的经典. 目前，密立根油滴实验已经成为很多高校大学物理实验的必做经典实验[1-3].

1 现有密立根油滴实验数据处理方法的缺陷

密立根在油滴实验中通过求各油滴电荷值的最大公约数的方法来确定油滴的电荷数. 但在实验教学过程中，由于所得到的油滴的电量并非整数而且有测量误差，因此直接计算少量油滴电荷量的最大公约数是不现实的做法. 目前大学物理实验中密立根油滴实验的数据处理，主要是采用“倒过来验证”的方法，即用公认的电子电荷e=1.602×10-19C去除实验测得的电荷量q，得到接近于某一整数的数值，这个整数就是油滴所带的元电荷的数目n，再用n去除实验测得的电荷量q，即得到电子的电荷e[1-3]. 这种方法可较快地处理数据，是实验教学中应用较普遍的方法，但其颠倒了因果关系，学生无法体会到实验设计的目的和意义. 用这种方法处理数据，只能作为实验验证，而且在实验中不宜选用带电量比较多的油滴. 正因为如此，密立根油滴教学实验中的数据处理问题是实验教学研究关注的问题之一[4-14]. 除了“倒过来验证”法， 还有最小速度差值法[4]、油滴电量逐次相减法[5-6]、油滴电量平均值逐次相减法[7]、平衡电压与下落时间隐函数关系法和电量概率统计直方图法等数据处理方法[8-13]. 上述方法针对特定的数据量有各自的优点. 通过对大量油滴电荷数据的概率统计[9-10]发现，这些处理方法中，对电荷间隔的取值均没有明确的依据和说明，而且不同电荷分布区域的峰值的取值均采用简单的取平均值方法.

针对这些问题，在大量油滴电量数据的基础上，先利用极端数据剔除法找到最佳的电荷量分割区间，然后再用聚类分析方法确定不同电荷量区间实验数据分布的中心. 利用上述数据处理方法，可以得到比较好的元电荷的量值.

2 元电荷分布的取数最佳区间确定(极端数据剔除法)

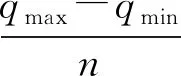
利用此方法对实验所得到的1 016个数据进行处理，最终计算得到合适的油滴电荷量取值间隔为0.029×10-19C. 这一间隔依赖于实验中所用的油滴数和油滴所带的电荷量. 参考文献[9-10]中用了取值间隔为0.02×10-19C，但未说明取此值的缘由，而且不同的油滴数和油滴电量取相同的间隔是不合理的. 用油滴电荷量取值间隔为0.029×10-19C这一数值整理油滴数的分布，结果如图1所示.

从图1可以看到，图中有比较明显的5个峰值区域，各峰的顺序和参量如表1所示，表中i为(由原点起)峰的序号，qi为峰顶对应电荷量，N为油滴出现次数.

表1 油滴电荷分布统计

图2 元电荷个数与油滴电荷量的关系图

从表1中数据可以估算，相邻峰值电荷量之差应为元电荷，由于所带电量必为元电荷的整数倍，直接对表1数据进行线性拟合，得到结果如图2所示. 直线的斜率1.525×10-19C即为元电荷的值，与公认值e=1.60×10-19C的相对偏差为4.7%.

上述方法是直接取各数据局域区域的峰值来计算元电荷，因而带有一定主观性. 为了充分利用大量的数据，同时给出合理的寻找数据分布中心的方法，尝试利用聚类分析对上述数据进行重新处理.

3 利用聚类分析确定实验数据分布中心

聚类分析是一种常用的无监督学习的机器学习方法，它可以将线性可分的数据划分成指定数量的目标类别. 而密立根油滴实验的数据是一维线性可分并且无监督的，所以尝试利用聚类分析中最常用的k-means聚类分析[15]将数据进行分割，从而对包含不同元电荷的数据进行了区别和分类，同时也选取聚类中心作为该类所带元电荷的值.

在图1中可发现数据普遍集中在2×10-19～8.5×10-19C的数值区间，并且呈现出4个峰值的分布状态. 因为若不同类别的数据量存在较大差异，则k-means聚类分析的误差较大，所以选取该连续分布且数据量密集的数值区间进行分析. 利用SPSS软件的k-means聚类分析功能，让k=4，将2×10-19～8.5×10-19C数值区间的数据进行聚类. 由于数据是准连续分布的，故聚类结果为各个元电荷的累积叠加，即若第i个聚类中心所包含的元电荷数为Ne，则第i+1个聚类中心所包含的元电荷数为Ne+1. 各聚类中心排序后，各个相邻中心之间的差值应接近单位元电荷的数值，故可估计出各聚类中心大致所含的元电荷数，结果如表2所示,其中q为所带电荷量,Ne为聚类中心所带元电荷数.

表2 各聚类中心油滴电荷分布统计

由于所带电量必为元电荷的整数倍，对各点进行线性拟合，得到结果如图3所示. 直线的斜率为1.527 1×10-19C即元电荷的值，与公认值e=1.60×10-19C相对偏差为4.6%，并且也显示了电荷电量的量子性.

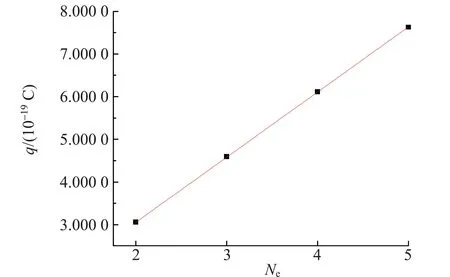
图3 利用聚类分析确定的元电荷个数与油滴电荷量的关系图

4 结 论

在大量油滴电荷数据的基础上，先利用极端数据剔除法找到最佳的电荷量分割区间. 电荷量分割区间的选取与实验数据量相关，因此相对于已有文献工作，本文提供了在大量油滴电荷数据中找出电荷量分割区间的方法. 找到最佳的电荷量分割区间后，用峰值法和聚类分析方法确定不同电荷量区间实验数据分布的中心. 峰值法简单直观，但有一定主观性；而聚类分析方法则是基于大量数据分布特点的机器学习方法. 利用上述2种寻找中心方法，均可得到较好的元电荷的量值，用峰值法和聚类分析方法得到的元电荷量值的相对偏差分别为4.7%和4.6%，满足实验要求.