对“基于Python和梯度下降算法的物理实验数据一元线性拟合方法”稿件的评审意见

朱鹤年

(清华大学 物理系，北京 100084)

来稿作者在教学任务较繁重的情况下坚持开展教学研究，同时学习现代应用统计学和人工智能领域的新方法，并力图引入基础物理实验教学中，这种努力和做法值得鼓励. 但是文章存在较多问题，有些问题是数据处理类文章的共性，现在指出如下.

1 科学追求包括数学严密性在内的逻辑自洽性

1)回归直线残差vi=(yie-yi)不是误差.

2)不能找各点到直线的距离最小解，只能使各点到直线距离在因变量方向投影之和为最小，即令因变量残差绝对值和最小.

3)残差绝对值Σ|vi|和与斜率无关，而距离绝对值之和与斜率有关，与单位(包括十进制)选择有关，是没有物理意义的量. 自变量单位确定之后，距离之和极小解不一定是最小二乘解.

4)在满足最小二乘前提条件(高斯-马尔科夫假定)时，在有解析解的多种回归方法或经典数值计算方法已被普遍应用的现状下，变换为人工智能等复杂问题中用的新方法，在绝大多数物理教实验学中可能是蛇足.

5)最小二乘判据的残差平方和、斜率相对标准差(或相对不确定度)、最小一乘判据的残差绝对值和、线性度指标这4个定量指标都是大学基础物理实验教学中可选择其一用于判断的指标. 至于与约定真值之差最小判据，从科学性原则看是最不应当采用的指标，该指标不是引导学生理性(有条件)质疑以分析讨论如何改进实验，而是引导学生寻找“歪打正着”式的好结果，易导致凑数，忽视科学理性精神的培养与熏陶. 科学追求包括数学严密性在内的逻辑自洽性，寻求主要源于实验的可重复或可比对的经验证据支持.

2 难于评定并回避不确定度是测量数据处理类文稿的关键瑕疵

国际计量局在《A concise summary of the International System of Units (8thedition, 2006)》的页首写道:“Metrology is the science of measurements, made at a known level of uncertainty, in any field of human activity.” 这说明了测量的普遍性和重要性，也说明了在测量结果中评定不确定度的必要性. 物理实验中，定性和半定量观测固然重要，但基于对物理量科学测量的定量研究通常更为重要. 大多数应用领域广泛遵循的ISO9000族标准中的本世纪的新体系《测量管理体系(MMS)》明文要求“MMS覆盖的每个测量过程都应评定不确定度. ”

对于物理实验教学研究中专门讨论数据处理方法的论文，不应回避不确定度评定问题. 应符合实验物理学、仪器仪表学和绝大多数工程技术测量对结果可信程度的表述. 而最小二乘法、最小一乘法(计量经济学中也较常见)等经典方法能够给出处理对象的不确定度.

在光电效应案例中，假如模型方程正确，来稿的新结果斜率“m=0.417 89”与以遏止电压为因变量方程最小二乘解的斜率0.421 48仅仅相差0.85%，差值小于P=95%时相对扩展不确定度Um/m≈19%的1/20，因此来稿结果是没有实质改变的.

3 关于检验拟合结果的指标

包含计量学的仪器仪表学和实验物理学，定量测量结果常常用于预测(报)或反预测(报). 不应当用相关系数作为直线回归的拟合优度判据，早就有陈希孺院士、统计学家方开泰教授、多位国内外专家、NIST及其前身NBS的手册《实验统计学》，都明文反对用相关系数评定拟合结果. 用两变量之间的相关系数曾经是国内物理教材的普遍性错误. 至于可决系数，虽然比相关系数有所改进，但仍然不能作为线性规律基本已知时拟合结果线性程度评价的独立参量，因为可决系数与回归的(或称拟合的)相关系数相近，它们只有与自由度一道才能反映拟合质量，因变量和自变量一定时它们的量值随回归模型(如是否过原点)、拟合方法(如最小二乘、最小一乘或其他稳健回归方法等)的不同而不同. 回归的(或称拟合的)相关系数，其定义不是两变量之间的相关系数，而是因变量与回归估值之间的相关系数.

IEC与中国国家标准已经有了一系列评价传感器建模线性程度的“线性度”的标准. 虽然在近代物理实验教学中全面推广线性度有困难，适当简化之后，用反映非线性相对误差限的“线性度”Uy/(ymax-ymin)，是不难引入近代物理实验的基础教学的，这里Uy是因变量的扩展不确定度. 另外，当测量目标只关注斜率时，用斜率的相对扩展不确定度(或简化要求时用相对标准差与自由度)，是教学中实用的简便方法.

建立新模型和已有模型回归(拟合)分析，是2个截然不同的研究问题. 计量经济学与社会、医学等方面的统计中，主要目的是建模；仪器仪表学、实验物理教学中，主要目的是基本已有模型再研究测量过程的方法设计改进或结果分析. 高校物理实验教学中涉及新建模型或者模型改进的很少. 建模问题可用测定系数等概念(包括与之近似的回归的相关系数)，因为建模问题一般不涉及应用该模型时的预报或者反预报的不确定度评定要求.

求出有限组实验数据的两变量之间的样本相关系数之后，两变量的总体相关系数的置信区间往往很大，特别是当样本数n较小时. 对于来稿光电效应案例，回归的(因变量电压与其回归估值之间的)相关系数为R=0.994 93，这与从可决系数所得结果相同. 审稿人根据统计学专著的表述规律中的曲线和尚欠完整的数表作近似计算，可以得出置信概率为0.95时，因变量电压与其回归估值之间总体相关系数的上下限分别为Rmax>0.999 59和Rmin<0.962 36，斜率相对不确定度为18.6% .

4 对物理规律的准确分析是选择数据处理模型与方法的前提

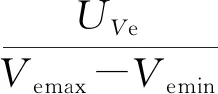
个别厂家为获得更接近普朗克常量约定真值的实验结果，刻意修改滤光片出厂时的中心波长值. 对于仪器设计缺陷，面上教学可改定量实验为半定量(或定性)实验，补充其他实验观察、观测与研讨的内容，探讨实验实际与理想条件间的不同或差距，更能激发学生的探索热情与质疑精神.

2)关于马吕斯定律的实验教学. 表述透射率和cos2θ成正比的马吕斯定律，只是垂轴透射比T2=0(消光比e为0)的近似. 普通薄膜偏振片和偏振棱镜的消光比一般在10-4～10-5量级. 当偏振器用在θ接近π/2的情形或用作消光调节时，宜采用完整式Tθ=(T1-T2)cos2θ+T2. 观察到实验物理与物理理论命题的不一致，正是物理实验教学的特点之一，在王之江主编的2版《光学技术手册》中，一开始就引入消光比非0的完整公式，而不是先讲马吕斯定律再修正之，这是更适合现代实验物理教学的思路. 如果只用马吕斯定律的公式建模，因为测量的实际始终是透射比，将出现因变量严重不等精密度的情形，原则上不能套用等精密度前提下的直线拟合公式与等权最小二乘法. 另外，通过实验学习新理论命题或者修正大学物理学的理论命题，在许多发达国家大学教育中也作为基础实验课程的内容(或任务)之一.