基于正态近似法的《周易本义·筮仪》概率分析

王晓刚, 宗序平

(1. 扬州职业大学, 江苏 扬州 225009; 2. 扬州大学, 江苏 扬州 225002)

董光璧先生的《易学科学史纲》(简称董著)中,利用古典概率模型,给出了《周易本义·筮仪》 “三变成一爻”的概率分布律:筮得“六”“七”“八”“九”的概率依次为1/16、5/16、7/16、3/16[1]。美国学者孙涤也曾作过类似推导[2]。

本文拟利用正态近似法对《周易本义·筮仪》(简称《筮仪》)作概率分析。

1 概率分析

引入如下记号:在第i变过程中,中分蓍策为二,左侧蓍策数与右侧蓍策数的差记为di,描述di离散程度的标准差记为σi,第i变后剩余蓍策数为ri(i=1,2,3)。

1.1 对随机变量d1分布的初步判断

首先对随机变量d1分布进行初步判断[3]。第一变中,49根蓍策,双手随机中分为二摞,包括最极端的情况,共有诸如“1与48”“2与47”……“48与1”共48种可能,其中“1与48”和“48与1”应剔除，以便后续的“挂一”及“归奇于扐”。按左减去右计算的差值d1绝对值较小的可能性较大,d1绝对值较大的可能性则较小。事实上,占筮者双手中分49根蓍策成左右两摞时,既不能刻意使左摞多于右摞,也不能刻意使右摞多于左摞。筮者在占筮时应该不偏不倚地将49根蓍策迅速分成左右两摞。这样就没有理由认为左摞多于右摞的概率,大于或小于右摞多于左摞的概率。合理的看法是左摞与右摞之差d1的总体期望值应该等于0。

各种偶然因素使得每一次操作的结果随机变化。根据概率论中的中心极限定理，有理由认为随机变量d1应该近似服从期望值为0的正态分布N(0,σ12)。

随机变量d1的取值空间是{±1,±3,…,±45}。严格来说,d1是一个离散型随机变量,正态分布是一种连续型分布,但在样本容量足够大条件下,可以用连续型分布的概率分布规律估计离散型随机变量取值的概率。这里具体做法是将d1所有取值按升序排序,用相邻两个值的中点将整个数轴分成若干个子区间,这样d1落在每一个子区间的概率就相当于d1取相应的值的概率。

为验证d1值服从N(0,σ12),同时也为了估计σ1值,操作了这样的随机试验:取49根筹策,双手迅速中分为两摞,记录左右数目并计算出左右之差后合为一摞,分别请100个人独立重复上述过程,得到含有100个差值的随机样本,详见表1。因为样本中没有小于-15的值,也没有大于15的值,所以-15对应区间(-∞,-14),15对应区间(14,+∞)。

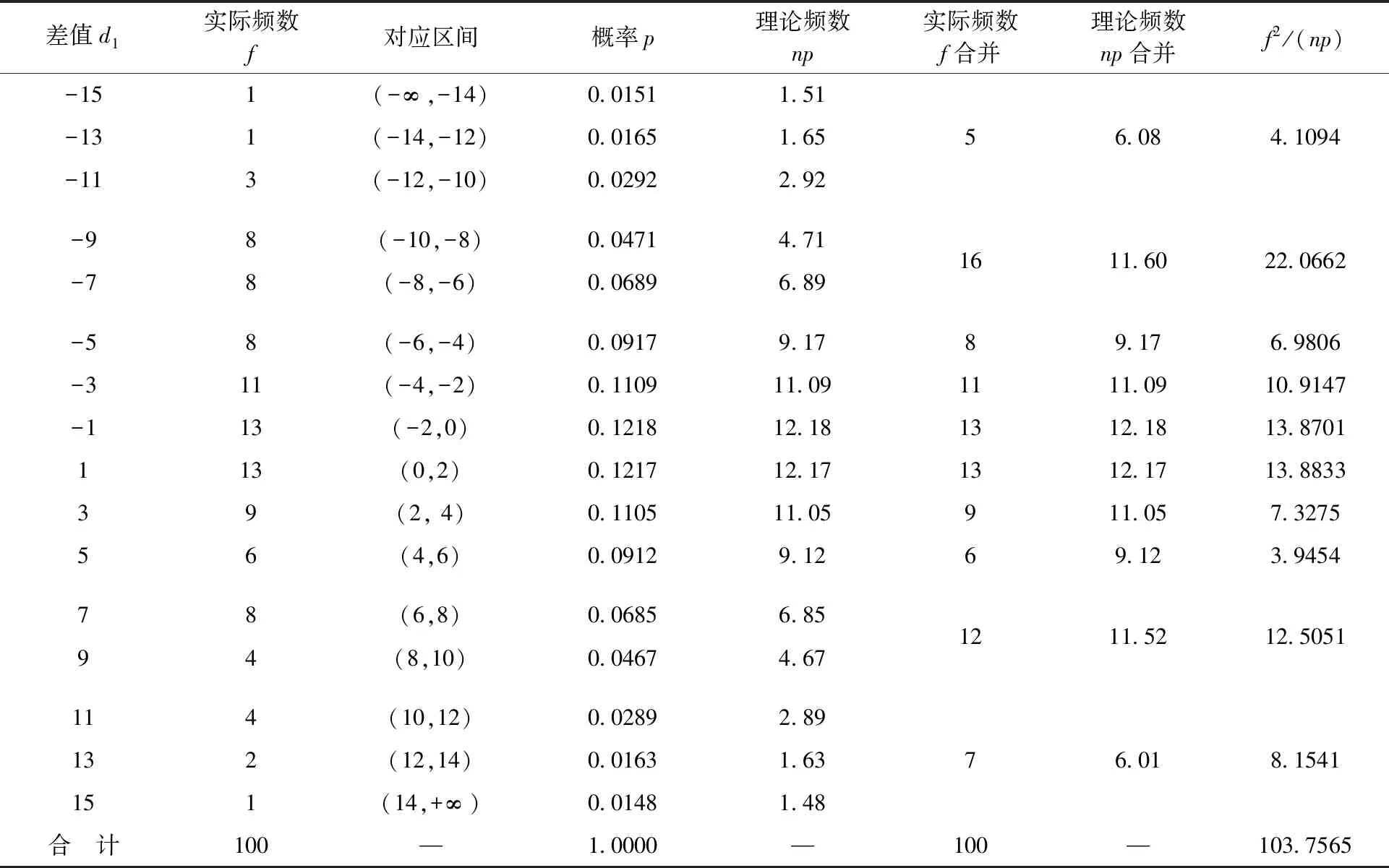
表1 对d1总体的抽样结果与分布拟合χ2检验计算表

假设总体d1近似服从正态分布,计算样本均值为-0.02,用以估计总体均值μ1,计算样本标准差为6.4479,用以估计总体标准差σ1,利用下式计算概率值:

(1)

如果总体d1确实近似为一个正态总体,那么表1中的实际频数f与理论频数np就不应该相差太大,衡量这一差距的统计量是按下式计算的χ2统计量。

(2)

因为分布族的χ2拟合检验是用连续分布近似估计离散分布,要求每一个区间上的理论频数np均大于5,所以表1中将d1的取值为-15、-13、-11三行，d1取值为-9、-7两行，d1取值为7、9两行，d1取值为11、13、15三行的频数与理论频数分别合并。这里n=100,公式(2)中的k是拟合项,这里k=10,表1的求和项为103.7565,代入(2)式计算得χ2=3.7565,χ2分布的自由度ν按ν=k-r-1计算,其中r表示分布中未知总体参数的个数,这里未知总体参数有2个,一个是总体均值,另一个是总体标准差,代入计算ν=7,利用χ2分布的概率分布函数可得显著性概率为0.8074,远大于一般情况下的显著性标准0.05,所以接受一开始的假设“d1总体是一个正态总体”,存伪的可能性很小,相反如果拒绝这一假设,那么弃真的概率则会高达80.74%。

(3)

1.2 第一变后剩余蓍策数r1的概率分布律

d1的取值空间是{±1,±3,…,±45},剩余蓍策数r1的取值空间是{40,44},并且r1=40对应d1∈{-41,-33,-25,-17,-9,-1,7,15,23,31,39},r1=44对应d1∈{-45,-43,-39,-37,-35,-31,-29,-27,-23,-21,-19,-15,-13,-11,-7,-5,-3,1,3,5,9,11,13,17,19,21,25,27,29,33,35,37,41,43, 45}。于是

P{r1=40}=P{d1=-41}+P{d1=-33}+

P{d1=-25}+P{d1=-17}+P{d1=-9}+

P{d1=-1}+P{d1=7}+P{d1=15}+

P{d1=23}+P{d1=31}+P{d1=39}

使用正态近似法有

(4)

为了完整探求P{r1=40}随σ1在其99.9%置信区间 (5.20, 8.34)中的变化规律,将公式(4)看成是以σ1为自变量，以P{r1=40}为函数值的函数。利用数学软件[4]，作出该函数在一个比(5.44, 7.87)更加宽泛的范围，比如(1,16)中的图象,如图1。图象表明σ1在区间 (5.20, 8.34)中自由变化时,P{r1=40}稳定于0.25附近,分别将σ1的99.9%置信区间的上下限σ1=5.20与σ1=8.34代入,可得P{r1=40}的值分别是0.2500760176与0.2500000129,所以认为P{r1=40}=1/4是合适的,从而P{r1=44}=3/4,其中的细微差异可以部分归结于用连续分布规律估计离散型随机变量概率所造成的误差。

图1 P{n=40}随σ1变化规律

1.3 第二变的概率分析

对第二变的概率分析,首先在r1=40与r1=44两种情况下,讨论r2条件分布。

采用与第一变类似的分析过程可得

P{r2=32|r1=40}=P{r2=36|r1=40}=1/2

P{r2=36|r1=44}=P{r2=40|r1=44}=1/2

根据全概率公式可得随机变量r2的概率分布律如下:

P{r2=32}=P{r1=40}×P{r2=32|r1=40}

=1/4×1/2=1/8

P{r2=36}=P{r1=40}×P{r2=36|r1=40}+

P{r1=44}×P{r2=36|r1=44}

=1/4×1/2+3/4×1/2=1/2

P{r2=40}=P{r1=44}×P{r2=40|r1=44}

=3/4×1/2=3/8

1.4 第三变的概率分析

第三变的概率分析应在r2=32、r2=36与r2=40三种情况下,讨论r3条件分布。与前类似有

P{r3=24|r2=32}=P{r3=28|r2=32}=1/2

P{r3=28|r2=36}=P{r3=32|r2=36}=1/2

P{r3=32|r2=40}=P{r3=36|r2=40}=1/2

从而

P{r3=24}=P{r2=32}×P{r3=24|r2=32}

=1/8×1/2=1/16,

P{r3=28}=P{r2=32}×P{r3=28|r2=32}+

P{r2=36}×P{r3=28|r2=36}

=1/8×1/2+1/2×1/2=5/16

P{r3=32}=P{r2=36}×P{r3=32|r2=36}+

P{r2=40}×P{r3=32|r2=40}

=1/2×1/2+3/8×1/2=7/16

P{r3=36}=P{r2=40}×P{r3=36|r2=40}

=3/8×1/2=3/16

于是三变而成一爻,占得老阴、少阳、少阴、老阳的概率分布律见表2。这一结论同于董著。

表2 《筮仪》三变成一爻的概率分布律

初步观察可知,占得阳爻与占得阴爻的概率各占1/2,阴阳平衡。占得变爻(老阴或老阳)的概率为1/4,占得少阳或少阴的概率为3/4,占得变爻的概率较低。

2 关于《筮仪》筮法概率分析的两点说明

第一,每一变之结果的概率分布所表现的稳定性,反映出《筮仪》筮法设计之巧妙。古圣先贤仅凭手中的一把蓍策模拟天地四时人事的变化,究竟是如何完成这样一个令人叹为观止的天才设计,今人已不得而知。这种稳定性表明,不管是什么样的占筮者、不管在什么样的条件下、不管使用的是什么样的占筮工具,三变而成一爻的概率分布均相同,这其中蕴含着非同寻常的哲学意义。著名的历史学家、经学家、儒学家金景芳先生早年强调《周易》的内容首先是筮，然后是卦，最后才是辞。在筮法当中有思想、有哲学、有所谓的“天之道”。研究《周易》必须先研究筮法,因为筮法本身就是哲学。研究《周易》的哲学思想,筮比卦更重要,至少说筮与卦同样重要。金景芳先生的论断无疑是精当的[5]。

第二,以上概率分析表明,每一变之结果的概率分布所表现的稳定性存在一定条件,即左右之差的总体标准差不能太大,也不能太小,这就要求卜筮者在“中分为二”时,要心无所系、操作迅速,既不能刻意使某一摞多于另一摞,也不能刻意追求左右平衡从而导致左右之差的离散度太小。实际经验表明,“中分为二”时,运作迅速,信手一分,一般均可满足要求。从d总体的总体标准差的99.9%的置信区间中也可看出这一点。相反,如果“中分为二”时有选择地使某一侧的蓍策数较多而另一侧的蓍策数较少、没有做到不偏不倚,那么将会使得差值d的标准差较大;又或者如果“中分为二”时动作不够迅速，掺杂进人为因素，刻意使得左右蓍策数尽量平衡,那么将会使得差值d的标准差较小。图1表明这两种情况下占筮结果的概率分布将会与表2完全不同。古人强调“中分为二”时不偏不倚与动作迅速是有所根据的,并不是所谓的为了增加占筮过程神秘感。

3 《筮仪》筮法与《左传》《国语》筮例的拟合分析

《左传》《国语》两书关于《周易》的记载共二十二条。其中有六条纯以易经卦爻辞作为箴言进行说理,另有十六条筮例,占卦十七个[6],具体是观之否，屯之比，大有之乾，归妹之睽，蛊，大有之睽，复，艮之随，困之大过，明夷之谦，屯，屯之比，坤之比，泰之需，乾之否，屯之豫，泰之八。其中,第17例的“泰之八”存在较大争议,暂舍之不用[7]。这样所得的样本共16卦96爻,其中老阴少阳少阴老阳出现的频数汇总见表3。

表3 老阴少阳少阴老阳统计

统计学上作分布拟合检验时一般选择计算过程较为简单的χ2检验,但在利用χ2检验作分布拟合时,因为使用了连续型分布的概率分布规律计算离散型随机变量的概率,所以最终求得的显著性概率存在着一定的误差,因此，下面在多项分布的概率分布律的框架下,精确计算《筮仪》概率分布律与《左传》《国语》筮例拟合检验显著性概率,只是计算过程较为复杂,必须借助数学软件进行计算。

假设随机试验共有四种不同结果“六”“七”“八”“九”,在一次试验中出现的概率分别是1/16、5/16、7/16、3/16。现独立重复进行该试验96次,记“六”“七” “八”“九”出现的次数分别是X,Y,Z,(96-X-Y-Z),其中X=0,1,2,…,96,Y=0,1,2,…,(96-X),Z=0,1,2,…，(96-X-Y),则X,Y,Z的联合概率分布律为

i=0,1,2,…,96;

j=0,1,2,…,(96-i);

k=0,1,2,…,(96-i-j)

(5)

因为 “六”“七”“八”“九”出现的概率分别是1/16、5/16、7/16、3/16,所以独立重复进行96次该试验“六”“七”“八” “九”出现的理论频数分别是6、30、42、18,记之为向量(6,30,42,18)。实际试验时所得样本的实际频数向量与理论频数向量的距离较近的可能性较大,较远的可能性较小,这里的距离选择常用的欧氏距离。现在向量(10,32,43,11)与向量(6,30,42,18)的欧氏距离的平方等于70。在如公式(5)所示多项分布的样本空间中,求出与理论频数向量的距离的平方大于等于70的所有样本点对应的概率之和,就是《筮仪》概率分布律与《左传》《国语》筮例分布拟合检验的显著性概率P,具体表达式是

(6)

其中logical是指逻辑判别式(i-6)2+(j-30)2+(k-42)2+(96-i-j-k-19)2≥70。

利用数学软件计算得拟合检验显著性概率P=0.3421,比通常的显著性标准0.05大很多,接受假设“《筮仪》筮得‘六’‘七’‘八’‘九’的概率分布律与《左传》《国语》筮例相合”是恰当的。相反如果拒绝该假设,则弃真的概率将达34.21%。

4 结论

按照《筮仪》这一随机数发生器,只要在操作 “中分为二”时,既不刻意使左右数目悬殊,又不刻意追求左右数目平衡,那么占筮结果的概率分布相对于左右之差的离散度将表现出相当的稳定性。经过假设检验,为易学主流学派所接受的《筮仪》筮法筮得“六”“七”“八”“九”的概率分布律与《左传》《国语》中的实际筮例基本相合,也就是与东周时期的《周易》筮法基本相合,拟合度为34.21%,只是没有达到令人完全信服的高度,关于这一问题今后将进一步研究。