RIEMANN-HILBERT PROBLEMS OF A SIX-COMPONENT MKDV SYSTEM AND ITS SOLITON SOLUTIONS∗

Wen-Xiu MA(马文秀)

Department of Mathematics,Zhejiang Normal University,Jinhua 321004,China;Department of Mathematics,King Abdulaziz University,Jeddah,Saudi Arabia;Department of Mathematics and Statistics,University of South Florida,Tampa,FL 33620-5700,USA;College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao 266590,China;College of Mathematics and Physics,Shanghai University of Electric Power,Shanghai 200090,China;International Institute for Symmetry Analysis and Mathematical Modelling,Department of Mathematical Sciences,North-West University,Ma fikeng Campus,Private Bag X2046,Mmabatho 2735,South Africa E-mail:mawx@cas.usf.edu

Abstract Based on a 4×4 matrix spectral problem,an AKNS soliton hierarchy with six potentials is generated.Associated with this spectral problem,a kind of Riemann-Hilbert problems is formulated for a six-component system of mKdV equations in the resulting AKNS hierarchy.Soliton solutions to the considered system of coupled mKdV equations are computed,through a reduced Riemann-Hilbert problem where an identity jump matrix is taken.

Key words integrable hierarchy;Riemann-Hilbert problem;soliton solution

1 Introduction

It is known that the Riemann-Hilbert approach is one of the most powerful techniques to generate integrable equations and their soliton solutions[1].The approach starts with a kind of matrix spectral problems,which possess bounded eigenfunctions analytically extendable to the upper or lower half-plane.It is closely connected with the inverse scattering method in soliton theory[2].The normalization conditions at in finity on the real axis in constructing the scattering coefficients is used in solving the corresponding Riemann-Hilbert problems[1].Upon taking the jump matrix to be the identity matrix,reduced Riemann-Hilbert problems generate soliton solutions,whose special limits can lead to rational solutions and periodic solutions.Applications were made for a few integrable equations,including the multiple wave interaction equations[1],the Harry Dym eqution[3],the generalized Sasa-Satsuma equation[4]and the general coupled nonlinear Schrödinger equations[5].

We follow the standard procedure suited for Riemann-Hilbert problems,where the unit imaginary number i is consistently used.We,therefore,start with a pair of matrix spectral problems of the following form:

where λ is a spectral parameter,u is a potential,φ is an n×n matrix eigenfunction,A,B are constant commuting n×n matrices,and P,Q are trace-less n×n matrices.Their compatibility condition is the zero curvature equation

where[·,·]is the matrix commutator.To formulate a Riemann-Hilbert problem for this zero curvature equation,we adopt the following pair of equivalent matrix spectral problems

where ψ is an n×n matrix eigenfunction,and.The relation between φ and ψ is

This provides us with a possibility to have two analytical matrix eigenfunctions with the asymptotic conditions

where Instands for the identity matrix of size n.Then we try to determine two analytical related matrix functionswhich are analytical in the upper and lower half-planesand continuous in the closed upper and lower half-planes{z∈C|±Im(z)≥0},respectively,to build a Riemann-Hilbert problem

where

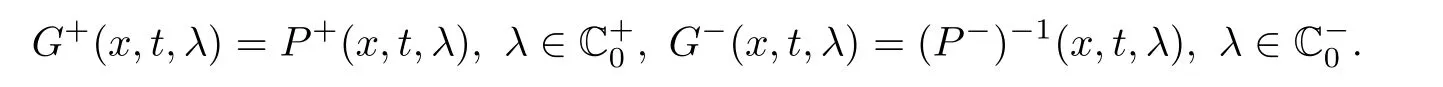
If we take the jump matrix G to be the identity matrix In,the corresponding Riemann-Hilbert problem can be normally solved,and soliton solutions can be generated through observing asymptotic behaviors of the matrix functions P±at in finity of λ.In this paper,we shall present an application example by considering a six-component system of mKdV equations and generate its soliton solutions by a special Riemann-Hilbert problem.

The rest of the paper is organized as follows.In Section 2,within the zero-curvature formulation,we rederive the AKNS soliton hierarchy with six potentials and furnish its bi-Hamiltonian structure,based on a new matrix spectral problem suited for the Riemann-Hilbert theory.In Section 3,taking a system of coupled mKdV equations as an example,we analyze analytical properties of matrix eigenfunctions for an equivalent spectral problem,and build a kind of Riemann-Hilbert problems associated with the newly introduced spectral problem.In Section 4,we compute soliton solutions to the considered six-component system of coupled mKdV equations from a speci fic Riemann-Hilbert problem on the real axis,in which the jump matrix is taken as the identity matrix.In the last section,we give a summary of the results and some discussions.

2 AKNS Soliton Hierarchy with Six Components

2.1 Zero Curvature Formulation

Let us first recall the zero curvature formulation to construct soliton hierarchies[6].Let u be a vector potential and λ,a spectral parameter.Choose a square spectral matrix U=U(u,λ)from a given matrix loop algebra.Assume that

solves the corresponding stationary zero curvature equation

Based on this solution W,we introduce a series of Lax matrices

where the subscript+denotes the operation of taking a polynomial part in λ,and ∆r,r≥ 0,are appropriate modi fication terms,and then generate a soliton hierarchy

from a series of zero curvature equations

The two matrices U and V[r]are called a Lax pair[7]of the r-th soliton equation in the hierarchy(2.4).Obviously,the zero curvature equations in(2.5)are the compatibility conditions of the spatial and temporal matrix spectral problems

where φ is the matrix eigenfunction.

To show the Liouville integrability of the soliton hierarchy(2.4),we normally furnish a bi-Hamiltonian structure[8]

where J and M form a Hamiltonian pair anddenotes the variational derivative(see e.g.,[9]).The Hamiltonian structures can be often achieved through the trace identity[6]

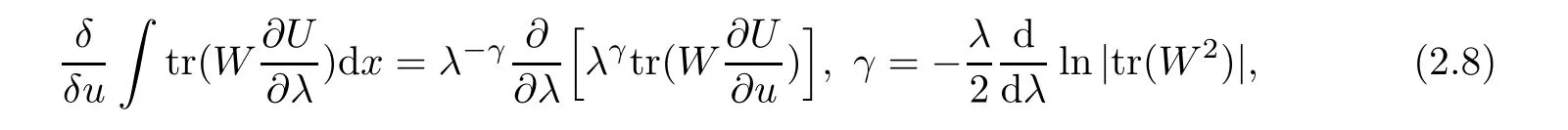
or more generally,the variational identity[10]

where h·,·i is a non-degenerate,symmetric and ad-invariant bilinear form on the underlying matrix loop algebra[11].The bi-Hamiltonian structure guarantees that there exist in finitely many commuting Lie symmetriesand conserved quantities

where n1,n2≥0,N=J or M,and K′stands for the Gateaux derivative of K with respect to u,

When the underlying matrix loop algebra in the zero curvature formulation is simple,the associated zero curvature equations engender classical soliton hierarchies[13];when semisimple,the associated zero curvature equations generate a collection of di ff erent soliton hierarchies;and when non-semisimple,we get hierarchies of integrable couplings[14],which require extra care in presenting soliton solutions.

2.2 AKNS Hierarchy with Six Components

Let us start with a 4×4 matrix spectral problem

where α1and α2are real constants,λ is a spectral parameter and u is a six-dimensional potential

A special case of p2=p3=q2=q3=0 transforms(2.10)into the AKNS spectral problem[15],and therefore it is called a six-component AKNS spectral problem.Since Λ=diag(α1,α2,α2,α2)has a multiple eigenvalue,the spectral problem(2.10)is degenerate.

To derive the associated AKNS soliton hierarchy,we first solve the stationary zero curvature equation(2.2)corresponding to(2.10).We suppose that a solution W is given by

where a is a scalar,bTand c are three-dimensional columns,and d is a 3×3 matrix.It is easy to see that the stationary zero curvature equation(2.2)becomes

where α = α1− α2.We look for a formal series solution as

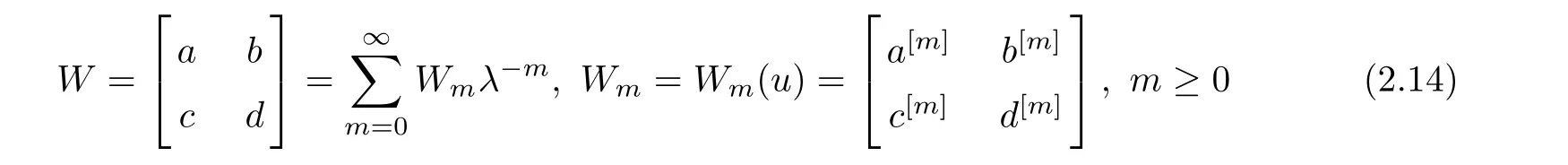
with b[m],c[m]and d[m]being assumed to be

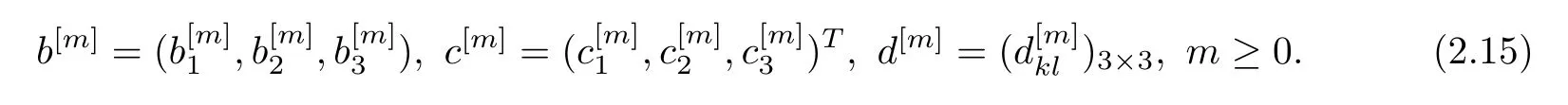
Then system(2.13)is equivalent to the following recursion relations

Let us now choose the initial values as follows

where β1,β2are arbitrary real constants and I3is the identity matrix of size 3,and take constants of integration in(2.16d)to be zero,that is,require

Thus,with a[0]and d[0]given by(2.17),all matrices Wm,m≥1,will be uniquely determined.For example,a direct computation,based on(2.16),generates that

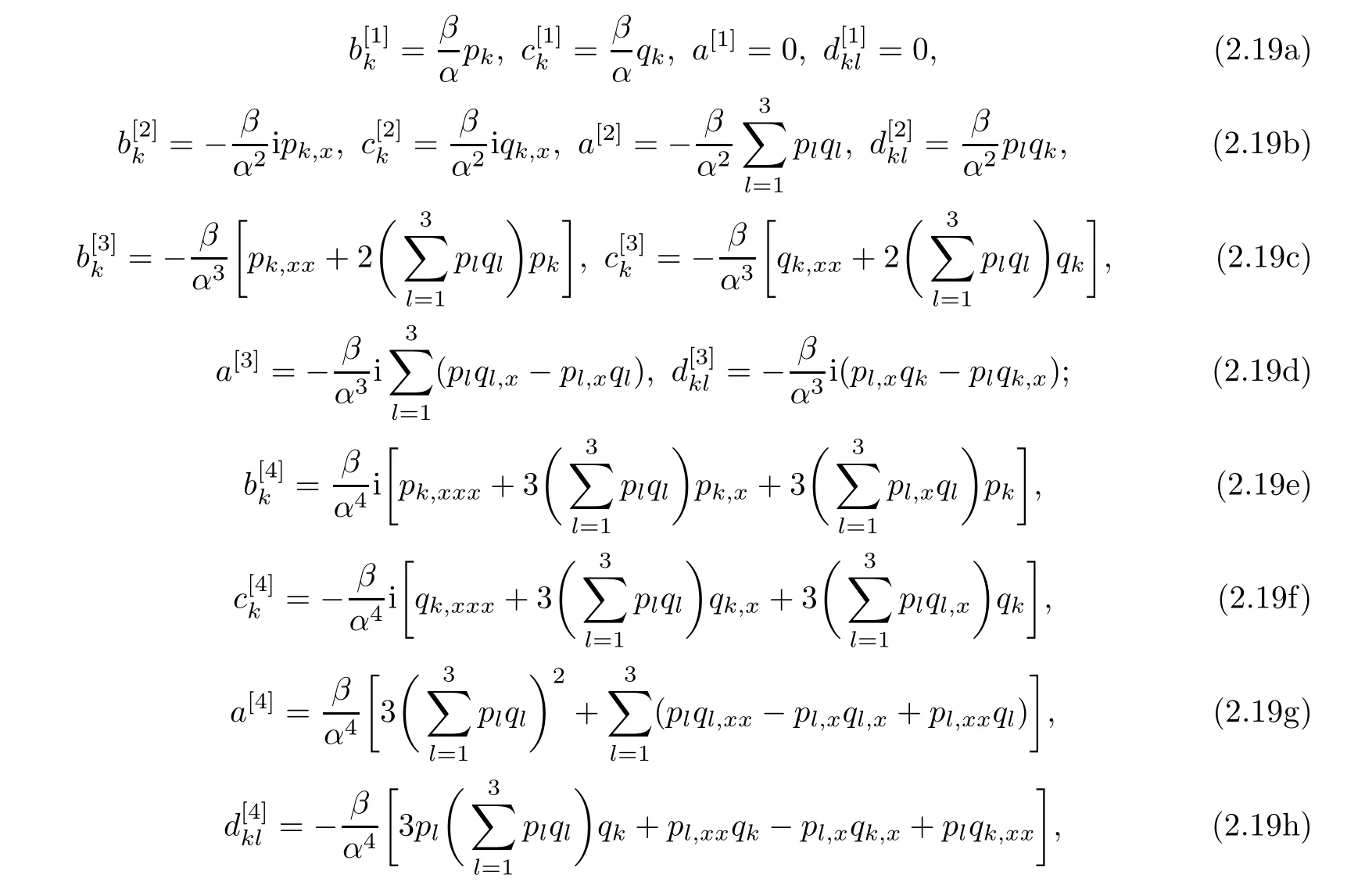
where β = β1−β2and 1 ≤ k,l≤ 3.Based on(2.16d),we can obtain,from(2.16b)and(2.16c),a recursion relation for b[m]and c[m],

where Ψ is a 6 × 6 matrix operator

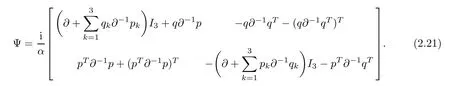
To generate the AKNS soliton hierarchy with six components,we introduce,for all integers r≥0,the following Lax matrices

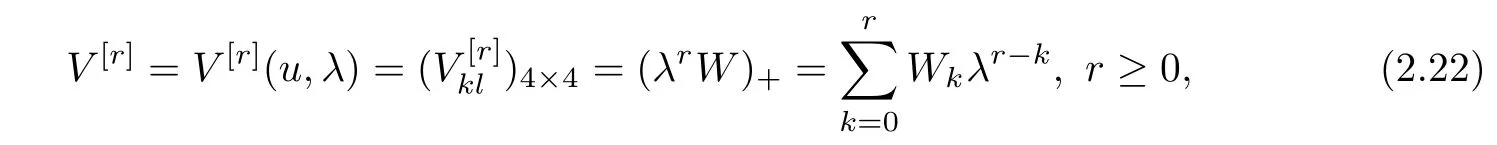
where the modi fication terms are taken as zero.The compatibility conditions of(2.6),i.e.,the zero curvature equations(2.5),lead to the AKNS soliton hierarchy with six components

The first two nonlinear systems in the above soliton hierarchy(2.23)read

and

which are the six-component versions of the AKNS systems of coupled nonlinear Schrödinger equations and coupled mKdV equations,respectively.Under a symmetric reduction,the sixcomponent AKNS systems(2.24)can be reduced to the Manokov system[16],for which a decomposition into finite-dimensional integrable Hamiltonian systems was made in[17],whileas the six-component AKNS systems(2.25)contain various systems of mKdV equations,for which there exist di ff erent kinds of integrable decompositions under symmetry constraints(see e.g.,[18,19]).

The AKNS soliton hierarchy(2.23)with six components possesses a Hamiltonian structure[12],which can be generated through the trace identity[6],or more generally,the variational identity[10].Precisely,we have

and

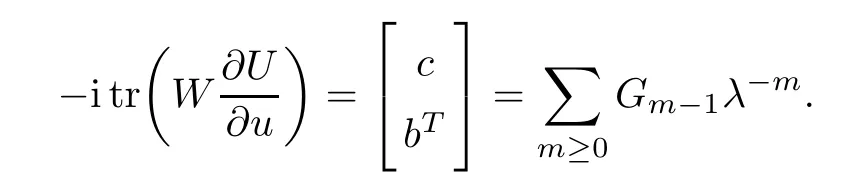
Inserting these into the trace identity and considering the case of m=2 tell γ=0,and thus

A bi-Hamiltonian structure of the six-component AKNS systems(2.23)then follows

where the Hamiltonian pair(J,M=JΨ)is de fined by

Adjoint symmetry constraints(or equivalently symmetry constraints)decompose the six-component AKNS systems into two commuting finite-dimensional Liouville integrable Hamiltonian systems[12].In the next section,we’ll concentrate on the six-component system of coupled mKdV equations(2.25).

3 Riemann-Hilbert Problems

The spectral problems of the six-component system of mKdV equations(2.25)are

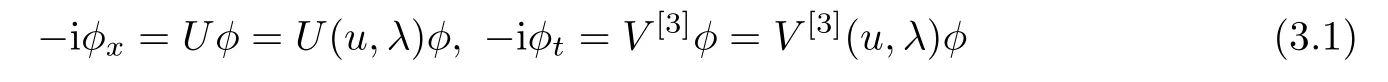
with

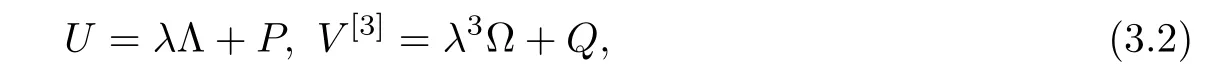
where Λ =diag(α1,α2,α2,α2),Ω =diag(β1,β2,β2,β2),and

u,p,q being de fined by(2.11),and a[m],b[m],c[m],d[m],1≤m≤3,being de fined in(2.19).

In this section,we discuss the scattering and inverse scattering for the six-component mKdV system(2.25)using the Riemann-Hilbert formulation[1](see also[20,21]).The resulting results lay the groundwork for soliton solutions in the following section.Assume that all the six potentials rapidly vanish whenorand satisfy the integrable conditions

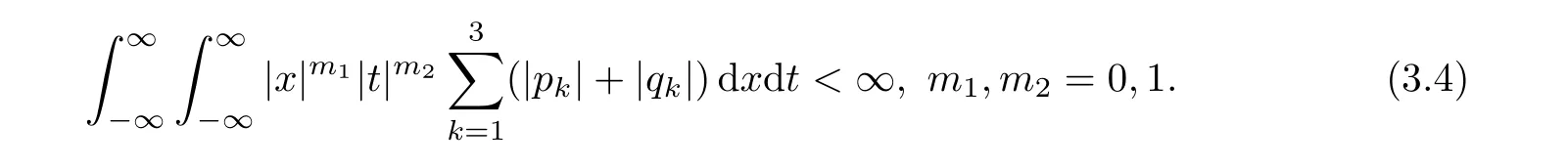
For the sake of presentation,we also assume that

From the spectral problems in(3.1),we note,under(3.4),that when x,t→±∞,we have the asymptotic behavior:Therefore,upon making the variable transformation

we have the canonical normalization

where I4is the identity matrix of size 4.The equivalent pair of spectral problems to(3.1)reads

by a generalized Liouville’s formula[22].

Let us now formulate an associated Riemann-Hilbert problem with the variable x.In the scattering problem,we first introduce the matrix solutions(x,λ)of(3.8)with the asymptotic conditions

respectively.The above superscripts refers to which end of the x-axis the boundary conditions are required.Then,by(3.10),we see detfor all x ∈ R.Sinceare both solutions of(3.1),they are linearly dependent,and therefore,one can have

where

is the scattering matrix.Note that detS(λ)=1 due to det.

Applying the method of variation in parameters and using the boundary condition(3.11),we can turn the x-part of(3.1)into the following Volterra integral equations for ψ±[1]:

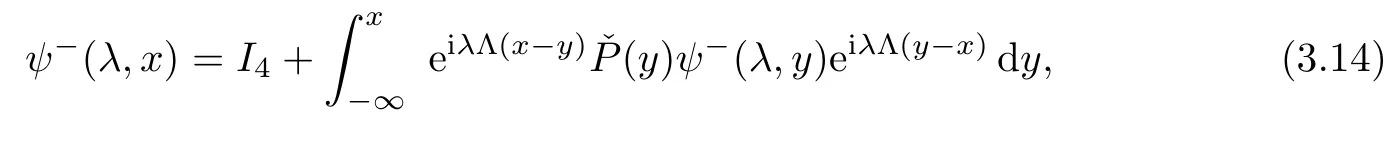
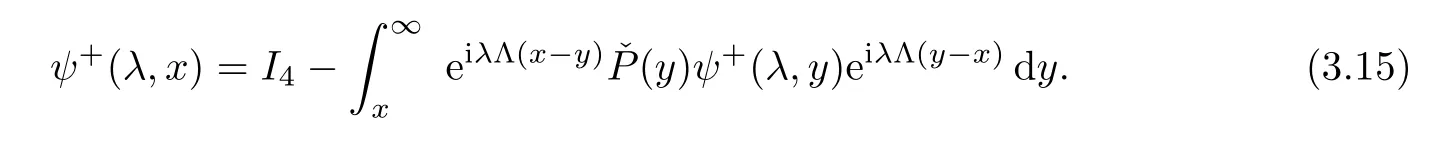
Therefore,ψ±allows analytical continuations o ffthe real axis λ ∈ R provided that the integrals on their right hand sides converge.Based on the diagonal form of Λ,we can directly see that the integral equation for the first column of ψ−contains only the exponential factor e−iαλ(x−y),which decays because of yx in the integral,when λ is in the closed upper half-plane.Thus,these four columns can be analytically continued to the closed upper half-plane.In a similar manner,we can find that the last three columns of ψ−and the first column of ψ+can be analytically continued to the closed lower half-plane.Upon expressing

is analytic in λ ∈ C+and continuous inand the matrix solution

is analytic in λ ∈ C−and continuous in,where

In addition,from the Volterra integral equation(3.14),we see that

and

Next we construct the analytic counterpart of P+in the lower half-plane C−.Note that the adjoint equation of the x-part of(3.1)and the adjoint equation of(3.8)read as

and

It is easy to see that the inverse matricesandsolve these adjoint equations,respectively.If we expressas follows

is analytic in λ ∈ C−and continuous in,and the other matrix solution

is analytic in λ ∈ C+and continuous inIn the same way,we see that

and

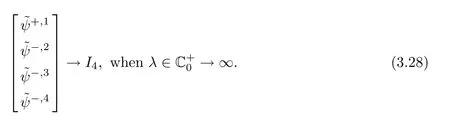
Now we have built the two matrix functions P+and P−,which are analytic in C+and C−and continuous inand,respectively.We can directly see that on the real line,the two matrix functions P+and P−are related by

where

where G is de fined by(3.30)and

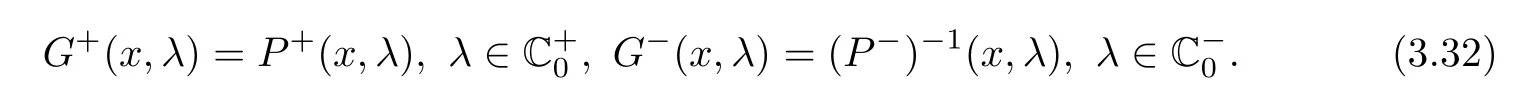
The asymptotic properties

provide the canonical normalization conditions for the presented Riemann-Hilbert problem.

To complete the direct scattering transform,let us now take the derivative of(3.12)with time t and use the vanishing conditions of the potentials.This way,we can show that S satis fies

which gives the time evolution of the scattering coefficients

4 Soliton Solutions

The Riemann-Hilbert problems with zeros generate soliton solutions and can be solved by transforming into the ones without zeros[1].The uniqueness of the associated Riemann-Hilbert problem(3.31)does not hold unless the zeros of detP+and detP−in the upper and lower half-planes are speci fied and the kernel structures of P±at these zeros are determined[23,24].From the de finitions of P±and the scattering relation between ψ+and ψ−,we find,using detψ±=1,that

where,based on detS=1,we have

Assume that s11has zeros{λk∈C+,1≤k≤N},andhas zerosTo get soliton solutions,we also assume that these zeros,λkandare simple.Then,each of kerP+(λk),1≤ k ≤ N,contains only a single column vector,denoted by vk,1≤k≤N;and each of kera row vector,denoted by

The Riemann-Hilbert problem(3.31)with the canonical normalization conditions in(3.33)and the zero structures in(4.3)can be solved explicitly[1,25],and thus one can readily work out the matrix P determining the potentials as follows.Note that P+is a solution to the spectral problem(3.8).Therefore,as long as we expand P+at large λ as

inserting this series expansion into(3.8)and balancing O(1)terms generate

which tells that

To compute soliton solutions,we set G=I4in the above Riemann-Hilbert problem(3.31).This can be achieved if we assume s12=s13=s14=s21=s31=s41=0,which means that no re flection exists in the scattering problem.The solutions to this speci fic Riemann-Hilbert problem can be obtained by(see e.g.,[1,25])

where M=(mkl)N×Nis a square matrix whose entries are de fined by

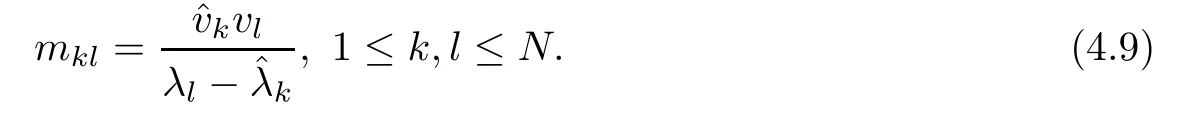
Note that the zeros λkandare constants,i.e.,space and time independent,and thus,we can easily determine the spatial and temporal evolutions for the vectors,vk(x,t)and1≤k≤N.For instance,let us compute the x-derivative of both sides of the equations

By using(3.8) first and then(4.10),we obtain

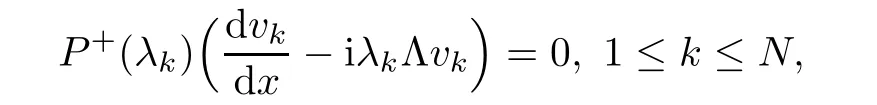
The time dependence of vk,

can be determined similarly through the t-part of the matrix spectral problem in(3.9).To conclude,we have

where wkandŵk,1≤k≤N,are arbitrary constant column and row vectors,respectively.

Finally,from the solutions in(4.8),we get

and thus further through the presentations in(4.7),the N-soliton solution to the six-component system of coupled mKdV equations(2.25)

5 Concluding Remarks

The paper is dedicated to formulation of Riemann-Hilbert problems and generation of associated soliton solutions to integrable equations.A crucial step is to take a kind of equivalent spectral problems,which guarantee the existence of analytical eigenfunctions in the upper or lower half-plane.We considered a 4×4 degenerate AKNS matrix spatial spectral problem and generated its soliton hierarchy possessing a bi-Hamiltonian structure.Taking the system of coupled mKdV equations as an example,we built its associated Riemann-Hilbert problems and presented an explicit formula for jump matrices.Upon taking the identity jump matrix in the presented Riemann-Hilbert problems,we computed soliton solutions to the considered six-component system of coupled mKdV equations.

The Riemann-Hilbert approach is very e ff ective in generating soliton solutions(see also,e.g.[3–5]).Moreover,it was generalized to solve initial-boundary value problems of integrable equations on the half-line[26].There are many other approaches to soliton solutions in the field of integrable equations,which include the Hirota direct method[27],the generalized bilinear technique[28],the Wronskian technique[29,30]and the Darboux transformation[31].Connections between di ff erent approaches would be interesting.About coupled mKdV equations,there were many other studies such as integrable couplings[32,33],super hierarchies[34]and fractional analogous equations[35],and an important topic for further study is a Riemann-Hilbert formulation for solving those generalized integrable counterparts.

It would be also particularly interesting to study other kinds of exact solutions to integrable equations,including positon and complexiton solutions[36,37],lump solutions[38–42],involutive solutions[43–46],and algebro-geometric solutions[47,48],using Riemann-Hilbert techniques.It is hoped that our results could be helpful in recognizing those exact solutions from the perspective of Riemann-Hilbert problems.

AcknowledgementsThe author would also like to thank Batwa S,Gu X,Ju L,Lafortune S,Maliso ffM,Manukure S,McAnally M,Tian J,Wang F D,Yong Y L,Zhang H Q,and Zhou Y for their valuable discussions.