A FOUR-WEIGHT WEAK TYPE MAXIMAL INEQUALITY FOR MARTINGALES∗
2019-05-31YanboREN任颜波
Yanbo REN(任颜波)
School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471003,China E-mail:ryb7945@sina.com
Abstract In this article,some necessary and sufficient conditions are shown in order that weighted inequality of the form
Key words weight;weak type inequality;martingale maximal operator;Young function
1 Introduction
Muckenhoupt[1]proved that two-weight weak type of(p,p)inequality holds for Hardy-Littlewood maximal function if and only if the couple of weights satis fies the Apcondition(1 The purpose of this article is to consider weighted inequality of the form The organization of this article is divided into two further sections.Some basic knowledge,which we will use,is collected in the next section.A four-weight weak type maximal inequality for martingales and its application to the case of two-weight are considered in Section 3. A Young function is a convex function given bywhere ϕ is a nonnegative,nondecreasing and right-continuous function on(0,∞).We call Φ an N-function if ϕ satis fies the following three conditions: Every N-function is strictly increasing and thus it has the inverse function.Notice that for an N-function Φ:Φ(at)≤ aΦ(t)when 0≤ a≤ 1,and aΦ(t)≤ Φ(at)when a≥ 1,t∈ (0,∞).The right-continuous inverse function of ϕ is given by The Young function given by is called the complementary function of Φ.Note that Ψ is an N-function if and only if so is Φ.Let us recall the Young inequality st≤Φ(s)+Ψ(t). Let(Φ,Ψ)be a pair of complementary N-functions,denote If Φ is a Young function,then RΦand SΦare continuous and increasing functions which map[0,∞)into itself and satisfy for every t≥0(see[8]). Throughout this article,we denote the set of non-negative integers and the set of integers by N and Z,respectively.We use C and C1to denote constants and may denote di ff erent constants at di ff erent occurrences. In this section,we devote to study a four-weight weak type maximal inequality for martingales.Some necessary and sufficient conditions for it are shown.First,we give a useful lemma. Lemma 3.1Let A be a sub-σ-algebra of F,(Φ1,Ψ1)and(Φ2,Ψ2)are two pairs of complementary N-functions,wi(i=1,2,3,4)are weights.Then the following statements are equivalent. (i) There is a constant C>0 such that holds a.e.for any positive random variable x. (ii) There are constants ε1>0 and C1>0 such that holds a.e.for any positive A-measurable random variable λ. (iii) There are constants ε2>0 and C2>0 such that holds a.e.for any positive A-measurable random variable λ. ProofWe complete the proof by showing thatand with ε1will be speci fied later.Then by(3.1),we have Now let ε1small enough such that ε1C<1 and ε1C2<1,then by(2.1),we obtain Now let k→+∞,we obtian(3.2). (ii)⇒(i) We can directly assume thata.e..Otherwise,we can similarly take a set B as above.Then by Young inequality and(2.1)we have Choose C large enough such thatwe then obtain(3.1). (iii)⇒(i) By Young inequality,we have that is It follows from(3.3)and the de finition of λ that The proof is completed. Remark 3.2If x is a random variable that is not equal to zero a.e.,then each of the inequality(3.2)and(3.3)is equivalent with the following inequality In fact,we only use the inequality|E(x|A)|≤E(|x||A)in the proof of Lemma 3.1. Now let us state our main result below. Theorem 3.3Let(Φ1,Ψ1),(Φ2,Ψ2)be two pairs of complementary N-functions and wi(i=1,2,3,4)be weights.Then the following statements are equivalent: (i) There is a constant C1>0,independent of f=(fn)n≥0∈ M,such that holds a.e.for any positive Fn-measurable random variable λ. (v) There are constants ε1>0 and C5>0 such that (iv) There are constants ε>0 and C4>0,such that holds a.e.for any positive Fn-measurable random variable λ. ProofBy the corollary of Lemma 3.1,we obtain(ii)⇔(iv)and(ii)⇔(v).Now we complete the proof by showing that(i)⇒(ii)⇒(iii)⇒(i). (i)⇒(ii) Suppose that(i)holds,and let(fn)n≥0∈ M.For any A ∈ Fnand λ ∈ (0,∞),we have For all k∈Z,set Bk={2k<|fn|≤2k+1}⊆{2k<|fn|},then for any B∈Fn, from which we obtain (ii)⇒(iii)is obvious. (iii)⇒(i) Let λ ∈ (0,∞),and de fine Then{τ< ∞}={f∗> λ}and|fτ|> λ on{τ< ∞}.Using(iii)we obtain The proof is completed. According to Theorem 3.3,we can easily show the following two corollaries. Corollary 3.4Let(Φ1,Ψ1),(Φ2,Ψ2)be two pairs of complementary N-functions and(u,v)a pair of weights.Then the following statements are equivalent: (i) There is a constant C1>0,independent of f=(fn)n≥0∈ M,such that (ii) There are positive constants ε and K,such that holds a.e.for any positive Fn-measurable random variable λ. Corollary 3.5Let(Φ1,Ψ1),(Φ2,Ψ2)be two pairs of complementary N-functions and(u,v)a pair of weights.Then the following statements are equivalent: (i) There is a constant C>0,independent of f=(fn)n≥0∈ M,such that (v) There are positive constants ε and K,such that holds a.e.for any positive Fn-measurable random variable λ. (vi) There are constants ε>0 and C>0 such that holds a.e.for any positive Fn-measurable random variable λ. Remark 3.6Corollary 3.5 gives some necessary and sufficient conditions for two-weight weak type maximal inequality.It was studied in[10]and[11],respectively.Here we use Theorem 3.3 to recondisider it,and a new equivalent condition((i)in Corollary 3.5)is presented.

2 Preliminaries







3 Main Results and Proofs












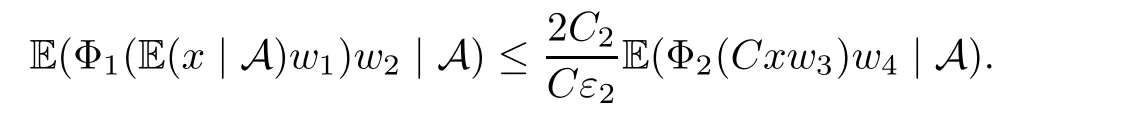




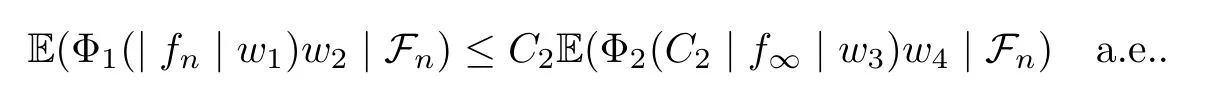


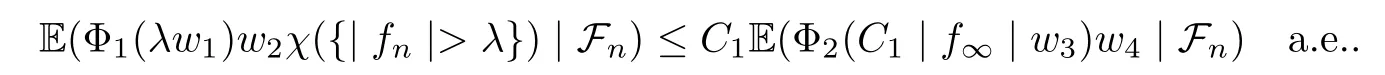













杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- RIGIDITY THEOREMS OF COMPLETE KÄHLER-EINSTEIN MANIFOLDS AND COMPLEX SPACE FORMS∗
- APPROXIMATE SOLUTION OF A p-th ROOT FUNCTIONAL EQUATION IN NON-ARCHIMEDEAN(2,β)-BANACH SPACES∗
- THE CHARACTERIZATION OF EFFICIENCY AND SADDLE POINT CRITERIA FOR MULTIOBJECTIVE OPTIMIZATION PROBLEM WITH VANISHING CONSTRAINTS∗
- RADIAL CONVEX SOLUTIONS OF A SINGULAR DIRICHLET PROBLEM WITH THE MEAN CURVATURE OPERATOR IN MINKOWSKI SPACE∗
- TIME-PERIODIC ISENTROPIC SUPERSONIC EULER FLOWS IN ONE-DIMENSIONAL DUCTS DRIVING BY PERIODIC BOUNDARY CONDITIONS∗
- ON INTEGRABILITY UP TO THE BOUNDARY OF THE WEAK SOLUTIONS TO A NON-NEWTONIAN FLUID∗
