RIGIDITY THEOREMS OF COMPLETE KÄHLER-EINSTEIN MANIFOLDS AND COMPLEX SPACE FORMS∗
2019-05-31TianCHONG种田
Tian CHONG(种田)
School of Sciences;College of Arts and Sciences,Shanghai Polytechnic University,Shanghai 201209,China
E-mail:chongtian@sspu.edu.cn
Yuxin DONG(东瑜昕)
School of Mathematical Science,Fudan University,Shanghai 200433,China E-mail:yxdong@fudan.edu.cn
Hezi LIN(林和子)
School of Mathematics and Computer Science,Fujian Normal University,Shanghai 200433,China E-mail:lhz1@fjnu.edu.cn
Yibin REN(任益斌)
College of Mathematics;Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China E-mail:allenrybqqm@hotmail.com
Abstract We concentrate on using the traceless Ricci tensor and the Bochner curvature tensor to study the rigidity problems for complete Kähler manifolds.We derive some elliptic di ff erential inequalities from Weitzenböck formulas for the traceless Ricci tensor of Kähler manifolds with constant scalar curvature and the Bochner tensor of Kähler-Einstein manifolds respectively.Using elliptic estimates and maximum principle,several Lpand L∞pinching results are established to characterize Kähler-Einstein manifolds among Kähler manifolds with constant scalar curvature and complex space forms among Kähler-Einstein manifolds.Our results can be regarded as a complex analogues to the rigidity results for Riemannian manifolds.Moreover,our main results especially establish the rigidity theorems for complete noncompact Kähler manifolds and noncompact Kähler-Einstein manifolds under some pointwise pinching conditions or global integral pinching conditions.To the best of our knowledge,these kinds of results have not been reported.
Key words rigidity theorems;Kähler-Einstein;complex space forms
1 Introduction
One of the major problems in geometry is to investigate the rigidity phenomena of some canonical geometric structures on manifolds.Various geometric invariants(tensors or quantities)have been introduced to measure the deviation of a general structure from some canonical one.For a Riemannian manifold,the traceless Ricci tensor measures the deviation from an Einstein manifold,while the Weyl curvature tensor measures the deviation from a conformal flat manifold.These tensors were used to establish some rigidity theorems for some special Riemannian manifolds(cf.[9,11,13,20,22,23]etc.).In[9],Hebey and Vaugon proved-type rigidity theorems for n-dimensional compact Riemannian manifolds with harmonic curvature and positive scalar curvature.In[11],Itho proved an isolation theorem of Weyl conformal tensor of positive Einstein manifold.In[13],Kim proved some-type rigidity theorems for noncompact complete Riemannian manifolds with harmonic curvature.The key point of their methods is a special type of di ff erential inequalities derived from a suitable Weitzenböck formula and a re fined Kato inequality,which enables one to use either the maximum principle or the elliptic estimates to derive the rigidity results,under either pointwise pinching conditions or global integral pinching conditions.
Over the past decades,much e ff ort was made to establish the existence of Kähler metrics with constant scalar curvature on a compact Kähler manifold(cf.[4,5,17,25]and the references therein).Among these metrics,Kähler-Einstein metrics form a notable subclass,which plays an important role in both complex geometry and physics.Besides the existence,the uniqueness and rigidity of these canonical Kähler metrics are also important for geometric applications.Back to early 1950’s,Calabi proved the uniqueness for Kähler-Einstein metrics with nonpositive scalar curvature.In 1986,Bando and Mabuchi[2]showed the uniqueness for Kähler-Einstein metrics with positive scalar curvature.Actually their uniqueness results were established within a given Kähler class.In[10],Itoh and Nakagawa obtained some local rigidity results of a Kähler-Einstein metric in the moduli space with Einstein metrics.On the other hand,complete noncompact Kähler-Einstein manifolds also received much attention[15,26–28].In 1949,Bochner introduced the so-called Bochner curvature tensor B on a Kähler manifold,which is an analogue of the Weyl curvature tensor.In[12],Itoh and Kobayashi established an isolation theorem of the Bochner curvature tensor of a compact Kähler-Einstein manifold.However,to the best of our knowledge,these kinds of rigidity problems for complete noncompact Kähler manifolds and complete noncompact Kähler-Einstein manifolds were not studied.
In this article,we study complete Kähler manifolds with constant scalar curvature and investigate the following two problems.
(A) The rigidity of Kähler-Einstein metrics among Kähler metrics with constant scalar curvature;
(B) The rigidity of Kähler metrics with constant holomorphic sectional curvature among Kähler-Einstein metrics.
Let(M,g,J)be a Kähler manifold with complex structure J and complex dimension m.As in the real case,we may use the traceless Ricci tensor E to measure the deviation of a Kähler metric from a Kähler-Einstein metric.It seems a little tautological to say that the Bochner curvature tensor measures the deviation of a Kähler metric from a Bochner flat Kähler metric.Nevertheless,for a Kähler-Einstein metric,the Bochner curvature tensor measures directly the di ff erence of its curvature tensor from that of the Kähler metric with constant holomorphic sectional curvature(see(4.1)in Section 4).
Roughly speaking,for problem(A),we prove that under either suitable pointwise pinching conditions or suitable Lmintegral pinching conditions on|E|and|B|,the Kähler manifolds become Kähler-Einstein manifolds(Section 3).For problem(B),we proved that under either suitable pointwise pinching conditions or suitable Lmintegral pinching conditions on|B|,the Kähler-Einstein manifolds become complex space forms(Section 4).These results may be regarded as a complex analogues to the rigidity results for Riemannian manifolds mentioned previously.Actually in[12],Itho and Kobayashi also considered problem(B)for compact Kähler-Einstein manifold and gave a similar Lm-pinching result to characterize CPm.However,their pinching constant is an abstract number depending on dimension and constant curvature.We may obtain a somewhat better result because our pinching constant seems better and more explicit than theirs.Moreover,our main work especially study problems(A)and(B)for complete noncompact Kähler manifolds and noncompact Kähler-Einstein manifolds.On the other hand,the authors in[21]established similar rigidity theorems for complete Sasakian manifolds with constant Pseudo-Hermitian scalar curvature.Finally,we would like to mention that the authors in[21]established similar results for complete Sasakian manifolds.
The main difficulties in proving our results lie in deriving some elliptic di ff erential inequalities from the Weitzenböck formulas for the traceless Ricci tensor of Kähler manifolds with constant scalar curvature and the Bochner tensor of Kähler-Einstein manifolds respectively.To overcome these difficulties,inspired by[8,9],we derive the Kato’s inequality for a(1,1)-type Codazzi tensor and use a similar technique in[8]to deal with a similar contracted term of the traceless Ricci tensor and the Weyl tensor in Weitzenböck formulas because a Kähler manifold can be decomposed into three orthogonal parts with respect to the Hermitian structure.
Our main results are as follows.The first part of this article is devoted to establishing the rigidity of Kähler-Einstein metrics among Kähler metrics with constant scalar curvature.First,we deal with the case of zero scalar curvature.
Theorem 1.1Let(M,g,J)be a complete noncompact Kähler m-manifold(m ≥ 2)with zero scalar curvature and positive Yamabe constant Λ(M,g).Assume that
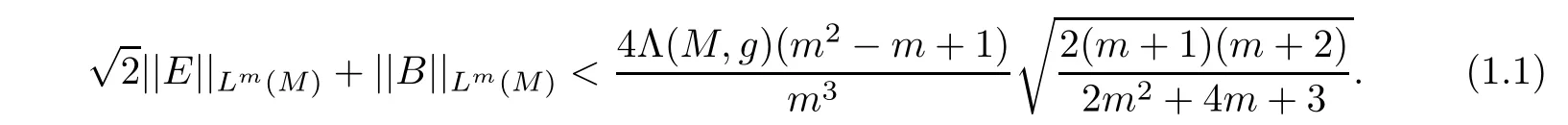
Then,M is a Ricci- flat Kähler manifold.
In the case of negative scalar curvature,we establish the following result.
Theorem 1.2Let(M,g,J)be a complete noncompact Kähler m-manifold(m ≥ 3)with constant negative scalar curvature R and positive Yamabe constant Λ(M,g).Suppose that

where Brdenotes a geodesic ball of radius r relative to some fixed point x0∈M.If then(M,g,J)is Kähler-Einstein.

The Bonnet-Myers theorem in Riemannian geometry implies that any complete Einstein manifold with positive scalar curvature must be compact.Thus,in the case of positive scalar curvature,we consider compact Kähler manifolds.The following two results are established under Lpand L∞pinching conditions,respectively.
Theorem 1.3Let(M,g,J)be a compact Kähler m-manifold(m ≥ 2)with constant positive scalar curvature R.If

Theorem 1.4Let(M,g,J)be a compact Kähler m-manifold(m ≥ 2)with constant positive scalar curvature R.If

then(M,g,J)is Kähler-Einstein.
The second part of this article investigates the rigidity of Kähler metrics with constant holomorphic sectional curvature among Kähler-Einstein metrics.We still begin with zero scalar curvature.
Theorem 1.5Let(M,g,J)be a complete noncompact Kähler-Einsteinm-manifold(m≥2)with zero scalar curvature and positive Yamabe constant Λ(M,g).If

then(M,g,J)is of constant holomorphic sectional curvature 0.Furthermore,if M is simply connected,then(M,g,J)is biholomorphically isometric to the complex Euclidean space Cm.
The case where R<0 is treated in the following theorem.
Theorem 1.6Let(M,g,J)be a complete noncompact Kähler-Einstein m-manifold(m≥4)with constant negative scalar curvature R and positive Yamabe constant Λ(M,g).If

and
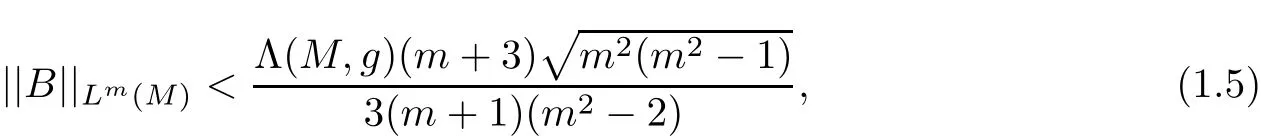
then(M,g,J)is of constant holomorphic sectional curvature
We also establish the two types of the rigidity results for the case of R>0(Theorem 4.2 and Theorem 4.3 in Section 4).Finally,using the above theorems enable us to deduce the results which characterize complex space forms among complete Kähler manifolds with constant scalar curvature(Theorem 4.5 to Theorem 4.8 in Section 4).
In order to prove our main results,we will derive the Weitzenböck formulas for|E|2and|B|2,respectively.First,it is worth noting that if the scalar curvature is constant,then E is a(1,1)-type Codazzi tensor.Next,if the metric is Kähler-Einstein,then B satis fies the second Bianchi identidy,which exhibits a Codazzi type property too.These properties for E and B,combined with some re fined Kato inequalities,enable us to deduce some di ff erential inequalities for|E|and|B|,respectively.
We treat these di ff erential inequalities on both complete noncompact and compact Kähler manifolds by means of elliptic estimates and maximum principle.Some Lpand L∞pinching results will be established to characterize Kähler-Einstein manifolds among complete Kähler manifolds with constant scalar curvature,and others will be given to characterize complex space forms among Kähler-Einstein manifolds.Consequently,we may also characterize complex space forms among complete Kähler manifolds with constant scalar curvature.
The outlines of the proofs of the main results are as follows.Before approaching the main results,we note that if the Yamabe constant Λ(M,g)>0,it provides a class of Sobolev-type inequality.The proof of Theorem 1.1 is straightforward.In this case,as the scalar curvature R is zero,the Sobolev inequality becomes Euclidean-type.With the help of a vanishing theorem for non-negative solutions of the Bochner-type di ff erential inequality(Lemma 2.2 in Section 2),we can easily complete the proof.Although in this case R<0,the Sobolev inequality also implies the Euclidean-type sobolev inequality,if we use the same method as in the proof of Theorem 1.1 to prove Theorem 1.2,we can not have a so-called nice gap result.Inspired by a technique in[13],we rewrite the di ff erential inequality as a integrated form.By picking up a family of cut-o fffunctions{φr}and a standard technic yields the result.We now turn to sketch our proofs of Theorem 1.3 and Theorem 1.4.We mentioned that any complete Einstein manifold with positive scalar curvature must be compact.Recall that if(M,g)is compact,the positivity of the scalar curvature guarantees the positivity of the Yamabe constant Λ(M,g).Thus,the Sobolev inequality(2.2)still holds.As the manifold is compact,we can directly integrate both sides of the inequality on M.Combining with the Sobolev inequality,it is easy to complete the proof of Theorem 1.3(see more details in Section 3).The proof of Theorem 1.4 can be concluded with the aid of a standard maximum principle.The same line of arguments allows us to prove the second part of our main results.More details will be postponed in Section 4.
This article is organized as follows.In Section 2,we give some standard notations and introduce some preliminary results.In Section 3,we consider complete Kähler manifolds with constant scalar curvature and prove the main results of the first part.In Section 4,we consider Kähler-Einstein manifolds and prove the main results of the second part.
2 Preliminaries
Let(M,g)be a smooth Riemannian n-manifold with dimension n≥2 and let Sgdenote the scalar curvature of g.The Yamabe constant is de fined by
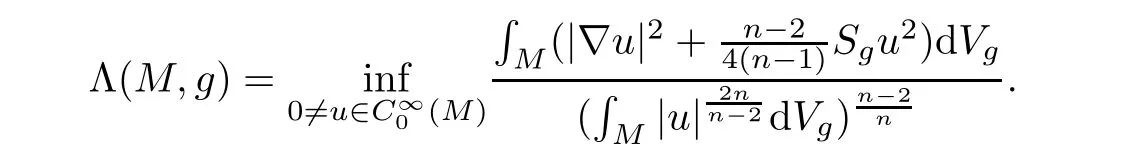

If Λ(M,g)>0,then one has the following Sobolev type inequality for any u∈(M).It is known that if(M,g)is compact,then the sign of Λ(M,g)is basically determined by the sign of the scalar curvature in a conformal class[6].However,there are complete noncompact Riemannian manifolds with both negative scalar curvature and positive Yamabe constant[7,24].
From now on,assume that(Mm,g,J)is a Kähler manifold with complex dimension m ≥ 2 and Λ(M,g)>0.Let(zα)be a system of local complex coordinates on M and let(1 ≤ α,β ≤ m)be the components of the Kähler metric in the coordinates.The inverse matrix of()is denoted by().Letanddenote the components of the curvature tensor and the Ricci tensor respectively.As usual,we will use the summation convention on repeating indices.The complex scalar curvature is de fined by R=.Note that Sg=2R.Then,the Sobolev inequality(2.1)becomes
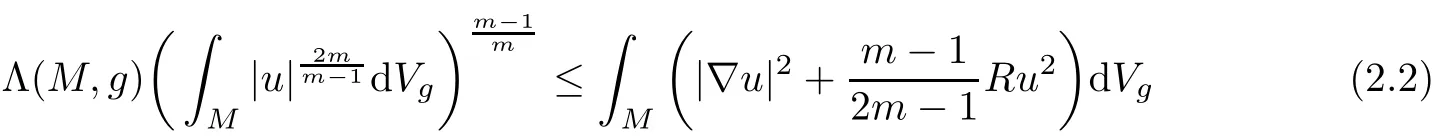
In[3],Bochner introduced the Bocher curvature tensor as follows

which may be regarded as a complex analogue of the Weyl curvature tensor.Clearly,the Bochner tensor B has the same algebraic symmetries as the curvature tensor of a Kähler metric.These includes

In addition,it has the following metric contraction property


Then,the Bochner curvature tensor may also be expressed as

For a Kähler manifold,the second Bianchi identity is reduced to
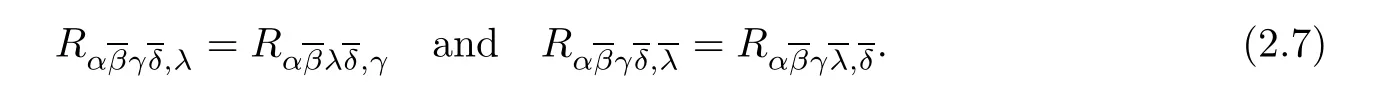
By contracting the indices α andin 2.7,we get
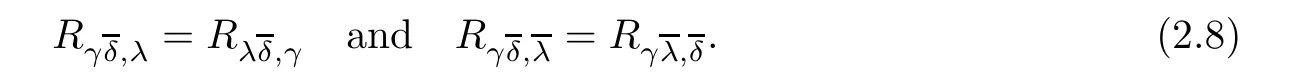
A(1,1)-type tensor is called Hermitian symmetric if the matrix of its components is Hermitian symmetric.An Hermitian symmetric(1,1)-type tensor field with properties(2.8)will be called a(1,1)-type Codazzi tensor.Clearly,the Ricci tensor field is a(1,1)-type Codazzi tensor.Thus,if the scalar curvature R is constant,then the traceless Ricci tensor field E is also a(1,1)-type Codazzi tensor.
The usual Ricci identity for commuting covariant derivatives gives

and
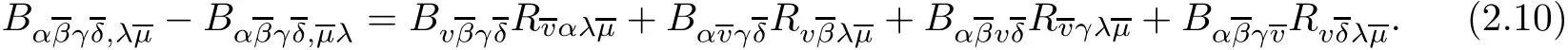
We need the following two lemmas.The first one is an algebraic inequality.
Lemma 2.1(Lemma 2.1 of[19]) Let λα,α =1,···,m,be real numbers.Ifthen
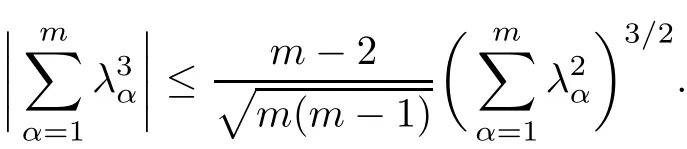
The next one is a so-called gap result for solutions of an elliptic di ff erential inequality.
Lemma 2.2(Proposition 3.1 of[20]) Let(M,g)be a complete Riemannian n-manifold on which the following Euclidean-type Sobolev inequality

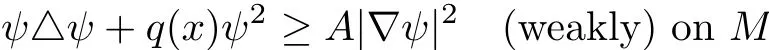
satisfying

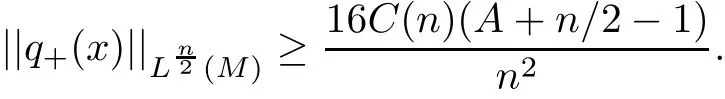
3 Rigidity of Kähler-Einstein Manifolds
In this section,we consider complete Kähler manifolds with constant scalar curvature.Some Lpand L∞pinching results will be established to characterize Kähler-Einstein manifolds among complete Kähler manifolds with constant scalar curvature.
Suppose that(M,g,J)is a Kähler manifold with constant scalar curvature.First,we intend to derive the Weitzenböck formula for the traceless Ricci tensor E.Note that E is a(1,1)-type Codazzi tensor and.For simplicity,one may choose a normal complex coordinate system at a given point.Using(2.6),(2.7),and(2.10),a direct computation gives

In[9],the authors deduced the Kato’s inequality for a traceless Codazzi tensor.Using a similar method,we may derive the following Kato’s inequality for a(1,1)-type Codazzi tensor.
Lemma 3.1Let C be a traceless(1,1)-type Codazzi tensor field on(Mm,g,J).Then,

ProofClearly,inequality(3.2)is equivalent to

For any given point p ∈ M,one may choose a system of complex coordinates(zα)such that
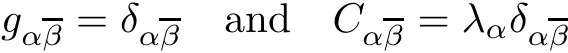

So,

First,we compute

Next,as C is a(1,1)-type Codazzi tensor,we discover that

In order to prove(3.3),one only needs to verify the following inequality
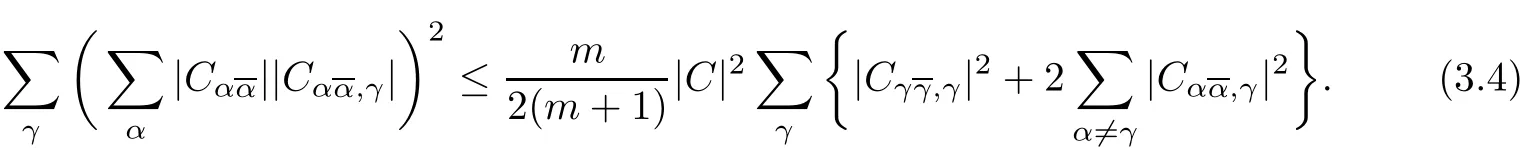
Set µα=for any fixed γ.Note that λα=.Consequently,
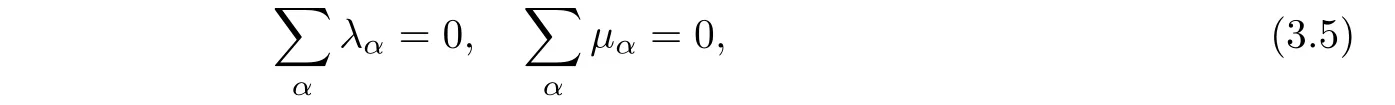
because C is traceless.It follows from(3.5)and Cauchy-Schwarz inequality that

Hence,we have
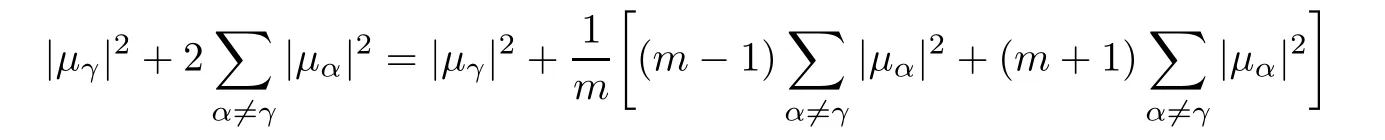

Using(3.6)and Cauchy-Schwarz inequality,we find
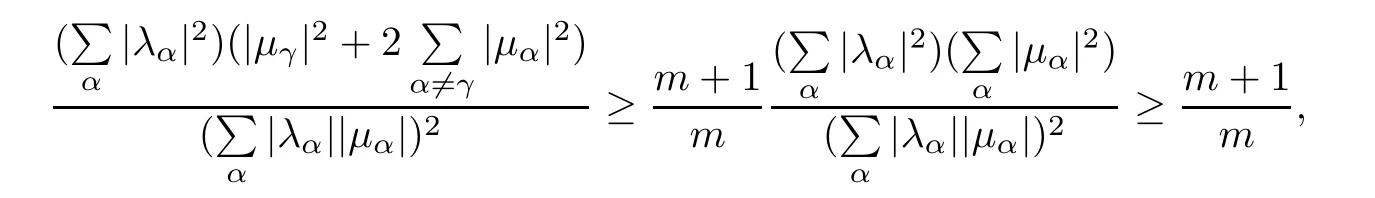
which implies immediately inequality(3.4).
Another equivalent expression of(2.5)is

which tells us that the curvature tensor of a Kähler manifold can be decomposed into three orthogonal parts with respect to the Hermitian structure.Now,we want to estimate the third term on the right hand side of(3.1)by using the same technique as in[8]for treating a similar contracted term of the traceless Ricci tensor and the Weyl tensor.
Lemma 3.2The inequality
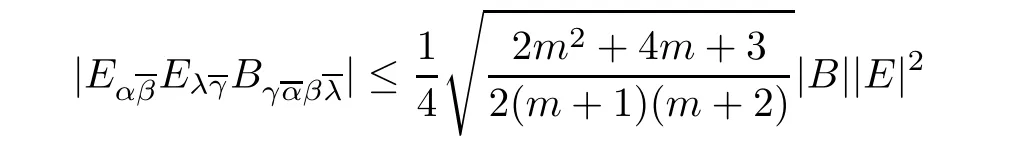
holds on any Kähler m-manifold.
ProofWe de fine a curvature-like tensor as

Clearly,V has the same symmetries as the curvature tensor of a Kähler manifold.So,it can be decomposed into three orthogonal parts with respect to the Hermitian structure:V=V1+V2+V3.Here,V1,V2,and V3correspond to the ‘Bochner curvature’part,the ‘traceless Ricci’part,and the ‘scalar curvature’part of V,respectively.To express Viexplicitly,let as introduce,whereandTherefore,the components of V2and V3are given by
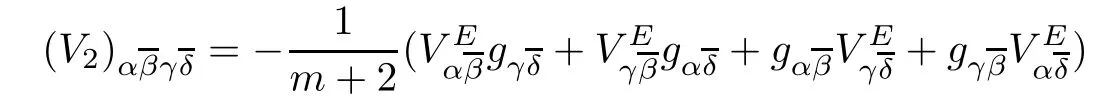
and

As before,we may assume gαβ=at a given point.From(2.4)and(3.7),we have
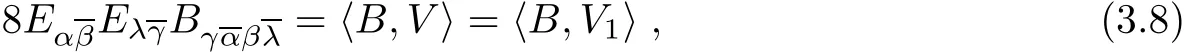

and

From(3.9)and(3.10),we deduce that

It follows from(3.8)and(3.11)that

Using Lemma 2.1 and Lemma 3.2,we get from(3.1)
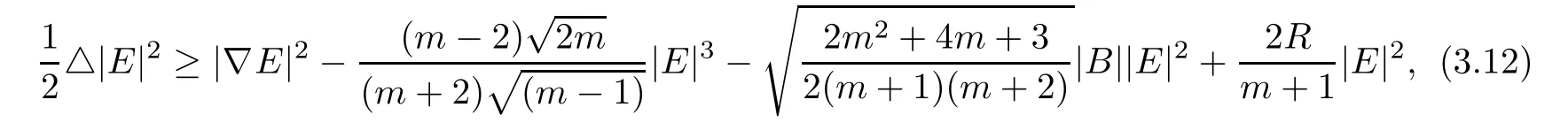
and thus using Lemma 3.1,we get
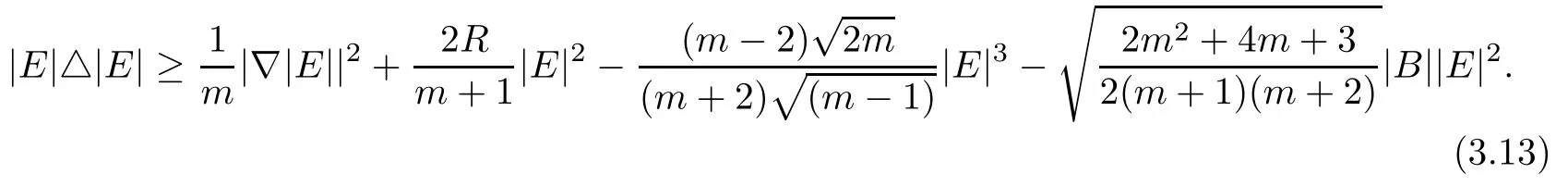
Proof of Theorem 1.1As R=0,di ff erential inequality(3.13)becomes

Under the assumptions that Λ(M,g)>0 and R=0,the Euclidean-type Sobolev inequality

We have to show that|E|=0.Clearly,(1.1)implies thatis finite,and thus

If|E|is not identically zero,applying Lemma 2.2 to(3.14),we obtain

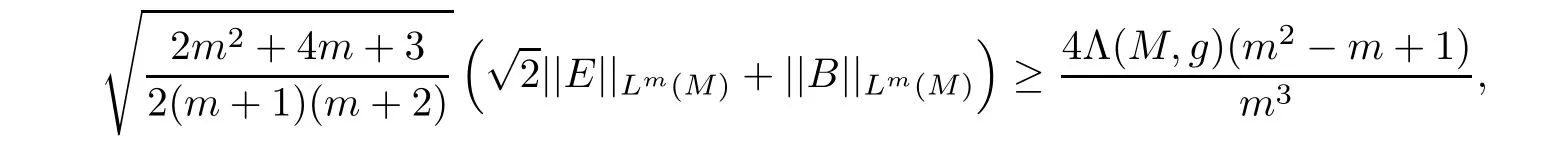
which contradicts to(1.1).Hence,we conclude that E=0,that is,(M,g,J)is Kähler-Einstein.
Next,we deal with the case that R<0.We mentioned that although in this case,Sobolev inequality(2.2)implies Euclidean-type Sobolev inequality(2.11)with C(n)=Λ(M,g)and n=2m,the direct application of Lemma 2.2 to(3.13)does not yield a nice gap result as in Theorem 1.1.Inspired by a technique in[13],we can prove Theorem 1.2.
Proof of Theorem 1.2Set u=|E|.For any test function 0≤φ∈(M),the di ff erential inequality(3.13)can be rewritten as
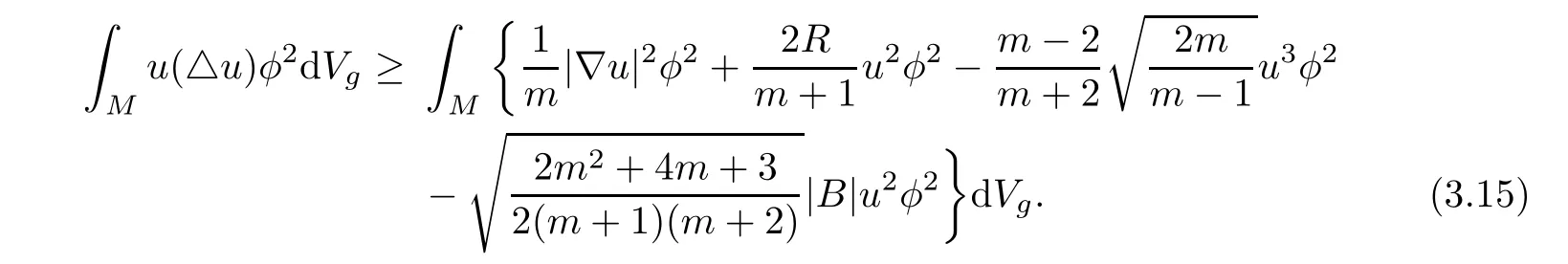
Using integration by parts and Schwarz inequality,we deduce that

for any ε1>0.It follows from(3.15)and(3.16)that
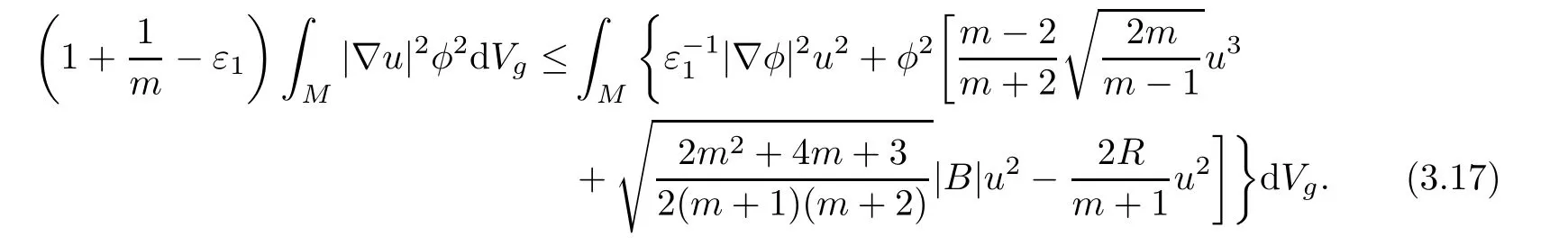
From the Sobolev inequality(2.2)and Schwarz inequality,we find
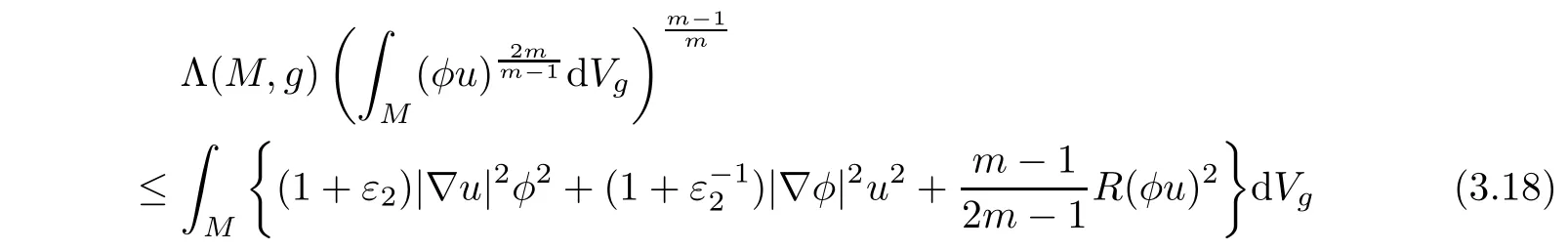
for any ε2>0.Then,(3.17)and(3.18)imply that

Note that A2>0 for m ≥ 3 and sufficiently small ε1and ε2.Under assumption(1.2),we may choose sufficiently small ε1and ε2such that

Moreover,the sufficiently small ε1and ε2also ensure
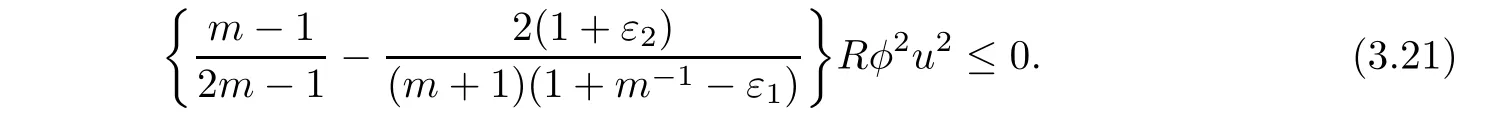

Hölder inequality gives

Hence,we may combine(3.20),(3.22)and(3.23)to find that

Consequently,we have

Now,let φ = φrbe a family of cut-o fffunctions satisfying

Then,(3.24)becomes

Now,we consider the case that R>0.Because any complete Einstein manifold with positive scalar curvature must be compact,recall that if(M,g)is compact,the positivity of the scalar curvature guarantees the positivity of the Yamabe constant Λ(M,g).
Proof of Theorem 1.3By integrating(3.13)and using Hölder inequality,we have

where
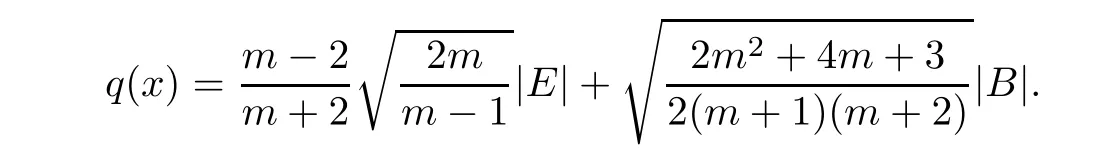
Because the condition R>0 implies Λ(M,g)>0,(2.2)gives
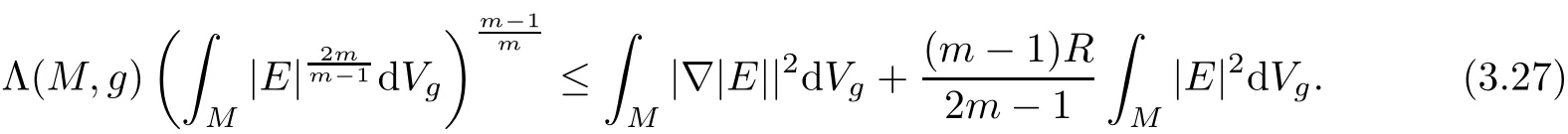
Substituting(3.27)into(3.26)leads to

Consequently,

Proof of Theorem 1.4From(3.12),we have
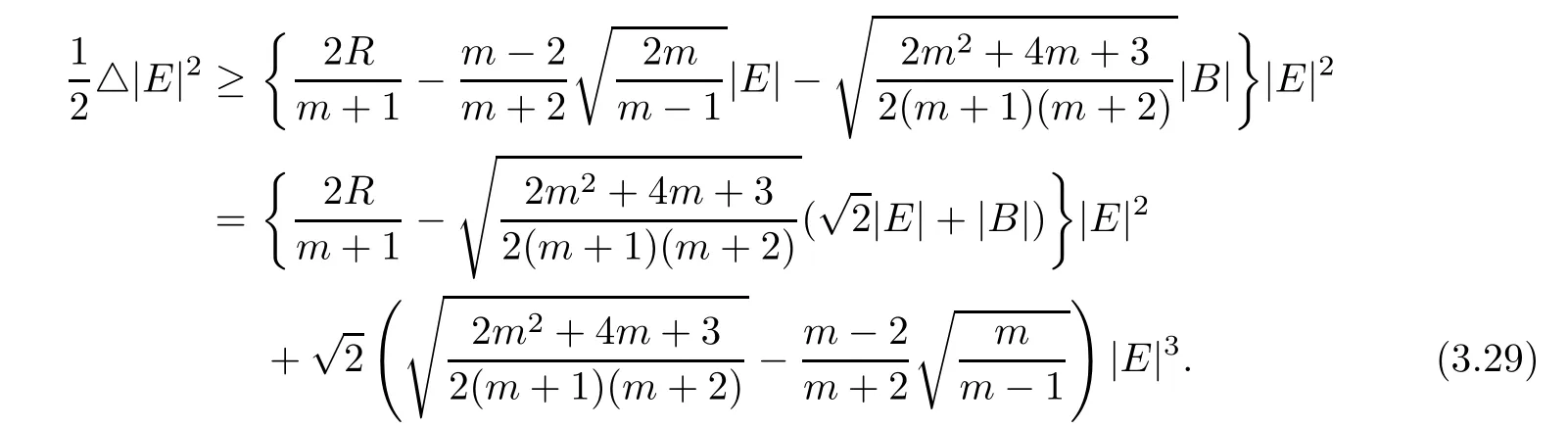
4 Rigidity of Complex Space Forms
In this section,we establish some rigidity results characterizing complex space forms among complete Kähler-Einstein manifolds and complete Kähler manifolds with constant scalar curvature respectively.
Suppose that(M,g,J)is a Kähler-Einstein manifold of dimension m(m ≥ 2).The Einsteinian condition implies directly that the scalar curvature R is constant and(2.6)becomes

Under this circumstance,the Bochner tensor measures the deviation of a Kähler-Einstein metric from the metric with constant holomorphic sectional curvature.
We want next to derive the Weitzenböck formula for the Bochner tensor B.Note that B is regarded as a real tensor in Λ1,1(M)⊗Λ1,1(M).As in Section 3,we take a normal complex coordinate system at a given point.So,.Using(2.4),(2.7),(2.10),and(4.1),a direct computation gives

Let us introduce two m2×m2Hermitian matrices H and K as follows

Then,(4.2)becomes
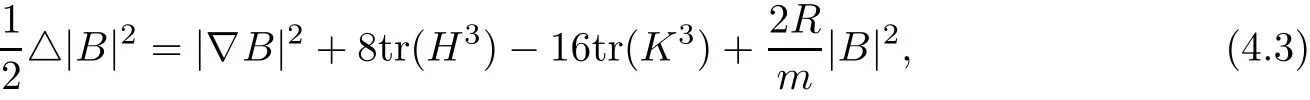

and
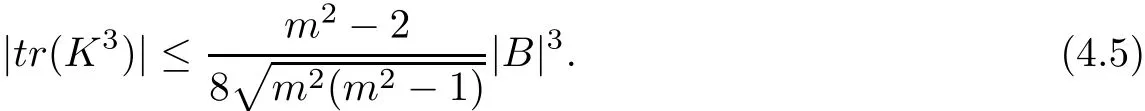
From(4.3),(4.4),and(4.5),we deduce that

In order to estimate the first term on the right hand side of(4.6),we need the following
Lemma 4.1((4.9),Lemma of[1]) Let T1and T2be tensors having the same symmetries as the curvature tensor and the covariant derivative of the curvature tensor of an Einstein metric on n-manifold respectively.Then,there exists δ(n)such thatwhereis a 1-form de fined byfor a tangent X.Moreover,if g is Kähler,we can take,where n=2m.
By applying Lemma 4.1 to T1=B and T2= ∇B,we find that.Note also that.Consequently,

Hence,(4.6)and(4.7)imply the following di ff erential inequality
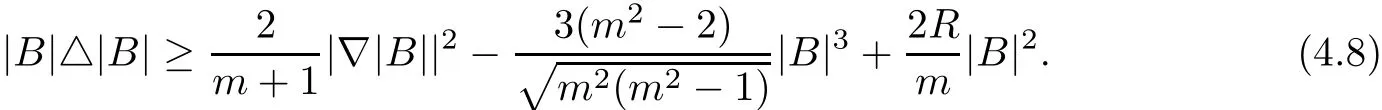
Proof of Theorem 1.5As R=0,Sobolev inequality(2.2)provides an Euclidean-type Sobolev inequality with Sobolev constant C(2m)=Λ(M,g),and(4.8)becomes


which contradicts to(1.4).Thus,B=0 and therefore,(4.1)yields that=0.This shows that(M,g,J)is of constant holomorphic sectional curvature 0.Consequently,if M is simply connected,then(M,g,J)is biholomorphically isometric to Cm(Theorem 7.9 in[14]).
Next,we present the rigidity result for the case R<0.As its proof goes almost the same way as that for Theorem 1.2,we describe the argument brie fly.
Proof of Theorem 1.6Set v=|B|.For any test function φ ∈(M),it follows from(4.8)that

As we derive(3.19)from(3.15),the same process allows us to get from(4.10)the following inequality

where
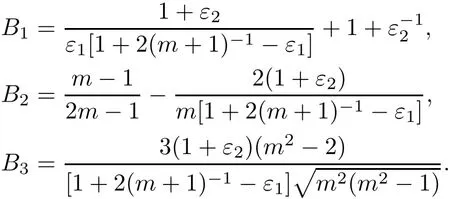
Note that B2>0 for m ≥ 4 and sufficiently small ε1and ε2.As R<0,we use the Hölder inequality to find that

Consequently,

Under assumption(1.5),we may choose sufficiently small ε1and ε2such that
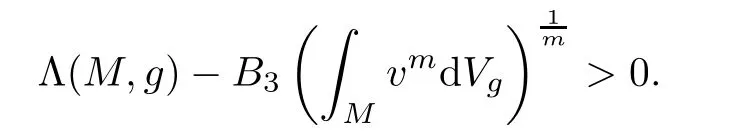
The remaining discussion is similar to that for Theorem 1.2.
By the solution of Yamabe problem,we know that the Yamabe constant Λ(M,g)is attained by a positive function u∈C∞(M).The metric,called the Yamabe metric,has constant scalar curvature given by[6,16]

It is known that any Einstein metric on a compact Riemannian n-manifold must be the Yamabe metric,provided it is not conformal to the standard metric of n-sphere[18].As(M,g,J)is Kähler-Einstein,g is the Yamabe metric in its conformal class[g].Hence,(4.11)implies that

Next,we give the two types of the rigidity results for the case of R>0.
Theorem 4.2Let(M,g,J)be a compact Kähler-Einstein m-manifold with m ≥ 2 and R>0.Set

If
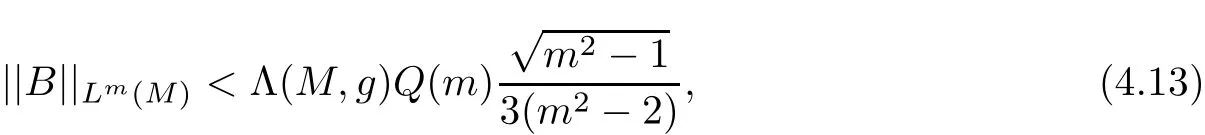
then(M,g,J)is biholomorphically homothetic to the complex projective space CPm.
Theorem 4.3Let(M,g,J)be a compact Kähler-Einstein m-manifold with m ≥ 2 and R>0.If

then(M,g,J)is biholomorphically homothetic to the complex projective space CPm.
Proof of Theorem 4.2By integrating(4.8)and using the Hölder inequality,we have
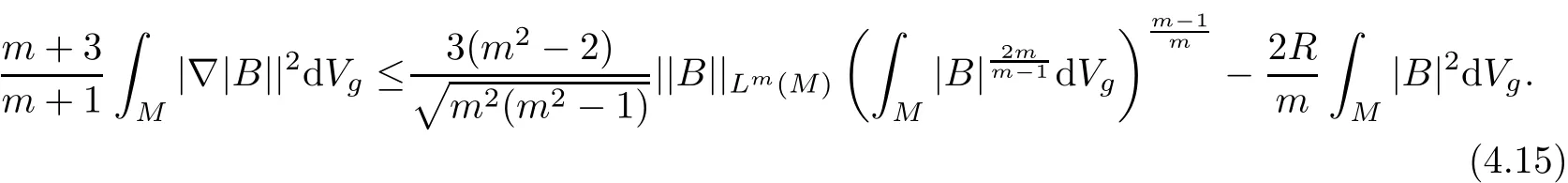
Applying(2.2)to|B|leads to

It follows from(4.15)and(4.16)that
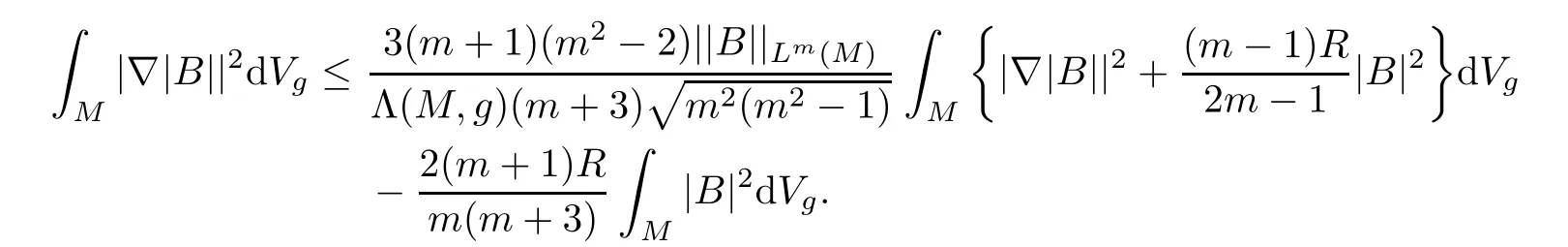
Consequently,we obtain
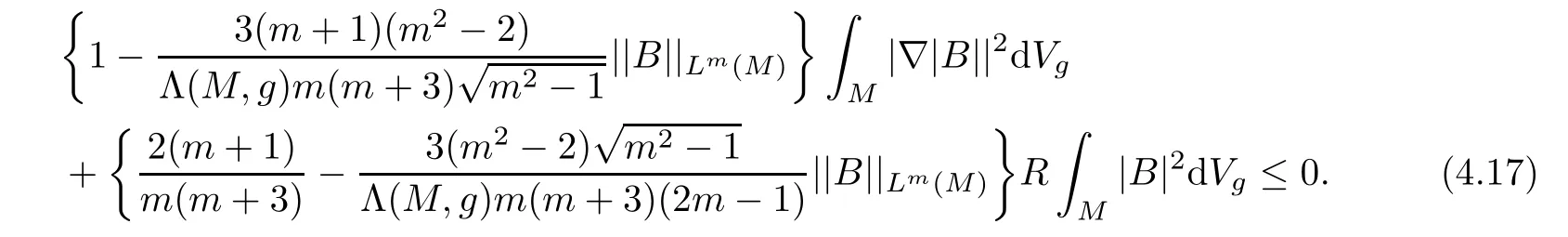
It is easy to verify that(4.13)implies that the two terms on the left hand side of(4.17)are nonnegative.This leads to B=0,that is,(M,g,J)has constant holomorphic sectional curvature.Then,Synge’s theorem ensures that M is simply connected.Hence,(M,g,J)is biholomorphically homothetic to the complex projective space CPmwith the Fubini-Study metric(Theorem 7.9 in[14],Vol.II).
Proof of Theorem 4.3From(4.6),we have
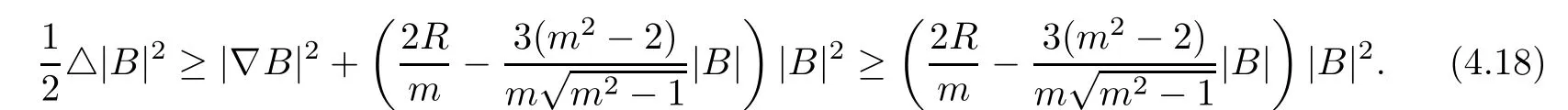
Under assumption(4.14),the integration of(4.18)implies immediately that B=0.Hence,(M,g,J)is biholomorphically homothetic to CPm.
Remark 4.4It is obvious that if condition(4.14)is replaced by
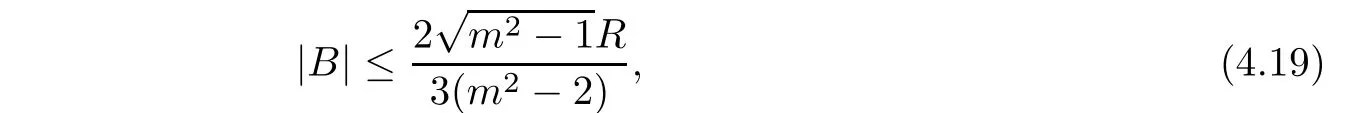
Finally,using the above theorems enable us to deduce the following results,which characterize complex space forms among complete Kähler manifolds with constant scalar curvature.
Theorem 4.5Let(M,g,J)be a complete noncompact Kähler m-manifold(m ≥ 2)with zero scalar curvature and positive Yamabe constant.If

then(M,g,J)has constant holomorphic sectional curvature 0.Furthermore,if M is simply connected,then(M,g,J)is biholomorphically isometric to Cm.
Theorem 4.6Let(M,g,J)be a complete noncompact Kähler m-manifold(m ≥ 4)with constant negative scalar curvature and positive Yamabe constant.If
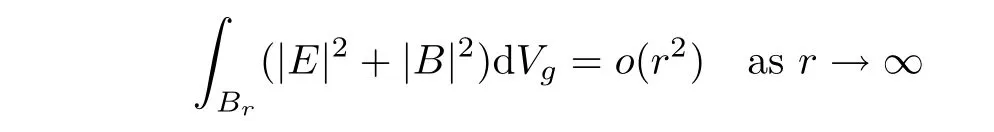
and
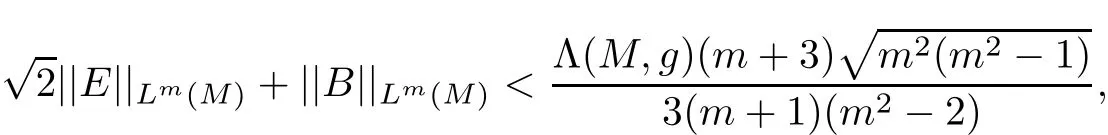
then(M,g,J)has constant holomorphic sectional curvature
Theorem 4.7Let(M,g,J)be a compact Kähler m-manifold(m ≥ 2)with constant positive scalar curvature.Let Q(m)be as in Theorem 4.2.If
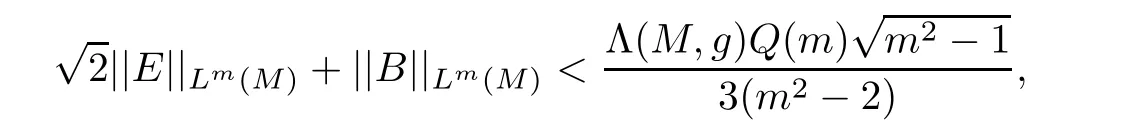
then(M,g,J)is biholomorphically homothetic to CPm.
Theorem 4.8Let(M,g,J)be a compact Kähler m-manifold(m ≥ 2)with constant positive scalar curvature R.Ifthen(M,g,J)is biholomorphically homothetic to CPm.
Proof of Theorem 4.5It is easy to verify that
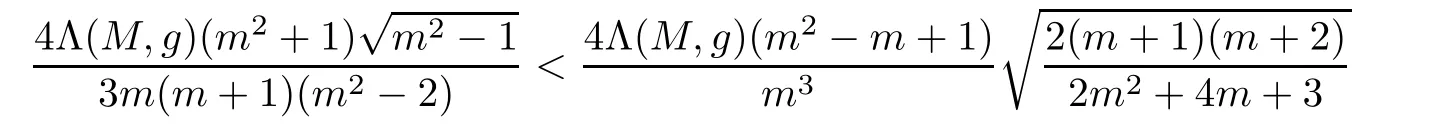
for m≥2.Then,using Theorems 1.1 and Theorem 1.5 successively,we may prove the assertions.
As

Theorems 1.2 and 1.6 can easily imply Theorem 4.6.One may verify that the pinching constant in Theorem 4.2 is smaller than that in Theorem 1.3.Likewise,we can directly have Theorem 4.7.Finally,Theorems 1.4 and 4.3 lead to Theorem 4.8.
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- NUMERICAL ANALYSIS FOR VOLTERRA INTEGRAL EQUATION WITH TWO KINDS OF DELAY∗
- LARGE TIME BEHAVIOR OF SOLUTION TO NONLINEAR DIRAC EQUATION IN 1+1 DIMENSIONS∗
- A NONTRIVIAL SOLUTION OF A QUASILINEAR ELLIPTIC EQUATION VIA DUAL APPROACH∗
- BLOW-UP PHENOMENA FOR A CLASS OF GENERALIZED DOUBLE DISPERSION EQUATIONS∗
- APPROXIMATE SOLUTION OF P-RADICAL FUNCTIONAL EQUATION IN 2-BANACH SPACES∗
- NEW BOUNDS ON EIGENVUALUES OF LAPLACIAN∗
